隧道下穿施工对夹层岩柱围岩应力影响研究
董捷,仲帅
隧道下穿施工对夹层岩柱围岩应力影响研究
董捷1, 2,仲帅1, 2
(1. 河北建筑工程学院 土木工程学院,河北 张家口 075000;2. 河北省土木工程诊断、改造与抗灾重点实验室,河北 张家口 075000)
为探明交叉隧道夹层岩柱围岩应力变化规律及其影响因素,开展重力条件下相似模型试验,采集新建隧道开挖期间夹层岩柱附加应力和既有隧道衬砌应变,并进行相应的数值计算。研究结果表明,新建隧道开挖完成后,交叉点处夹层岩柱中围岩应力急剧下降;受下部隧道开挖的影响,既有隧道轴向呈现“下凹”状态,由于应变监测断面两侧底部围岩应力相继释放,环向附加应变由非对称分布逐渐变为对称分布。夹层岩柱中围岩应力下降区域分布呈“漏斗”状,既有隧道的遮蔽效应使得交叉点处附加围岩应力小于其他部位;围岩条件较好时,既有隧道底部附加围岩应力较小,随着新建隧道开挖跨度和体积损失率的减小,地层中附加围岩应力也逐渐减小。
交叉隧道;围岩应力;模型试验;数值计算

随着我国交通运输事业迅速发展,公路、铁路线路越发密集,受地形和选线的制约,新建隧道下穿既有隧道工程频繁发生[1−2]。下穿隧道开挖会扰动周边岩土体,使得既有隧道产生附加内力及变形,夹层岩柱及隧道结构的力学行为也将变得极为复杂,当扰动达到一定限度时,会对既有隧道安全运营产生不利影响。在分析新建隧道开挖对临近隧道的影响时,理论解析方法概念明确,可便捷地为工程提供参考[3]。Klar等[4]采用弹性连续体解和Winkler模型解来计算新建隧道施工引起既有管线隧道的位移和弯矩。LIU等[5]提出一种基于Winkler模型的叠加方法,可以用来获取新建隧道零间隙下穿时既有隧道内力变化情况,并通过有限元验证了该方法的有效性。张冬梅等[6]基于Kerr地基梁理论,提出一种新建隧道施工对既有隧道影响的解析方法,分析了地层损失率等参数对隧道结构纵向变形的影响。由于隧道间相互作用的复杂性,许多学者建立三维仿真模型进行隧道近接施工的数值模拟研究。Ng等[7]进行三维有限元分析,研究了既有马蹄形隧道宽度和新建下穿隧道跨度比(B/D)对交叉隧道相互作用的影响。Avgerinos等[8]通过三维有限元方法,揭示了下穿隧道开挖过程中既有隧道内力和变形变化规律。林越翔等[9]建立盾构隧道精细化模型,对新建隧道正交下穿期间既有盾构隧道管片结构动静力响应特性进行了研究。来弘鹏等[10]依托西安地铁某交叉隧道工程,构建三维数值模型,研究了土仓压力、注浆压力、注浆量等参数对既有隧道沉降和轨道高差的影响。李玉峰等[11]从既有隧道沉降和支护结构内力方面考虑,分析了围岩级别、交叠角度和夹层围岩厚度等因素对交叉隧道施工的影响。此外,模型试验可以直观反映隧道间相互作用而被广泛使用。Ng等[12−13]开展了新建隧道正交下穿既有隧道离心模型试验,研究了既有隧道断面类型及隧道施工模拟方法对交叉隧道相互作用的影响,并进行了数值反演分析进一步了解新建隧道施工期间应力传递机理。MA等[14]进行了双隧道正交下穿既有管线隧道离心模型试验及三维数值模拟,分析了双隧道施工顺序对既有管线的影响。张晓清等[15]通过排液法模拟新建隧道盾构施工中的地层体积损失和质量损失,开展了隧道垂直下穿、上穿和上下穿越既有隧道情况下模型试验,研究了地表沉降特性和既有隧道纵向变形,并通过数值模拟对试验结果进行了验证。上述研究取得了丰硕的成果,然而这些研究内容多涉及新建隧道施工所导致的既有隧道受力、变形以及地表沉降,有关隧道近接施工期间夹层岩柱围岩应力的研究也都集中在新建隧道并列近接的情况[16−17],针对新建隧道下穿期间夹层岩柱围岩应力的研究则相对较少。隧道开挖会导致围岩应力重新分布,对于新建隧道下穿既有隧道工程,交叉区段竖向附加围岩应力是既有隧道产生附加内力及弯曲变形的重要影响因素[13]。因此,开展夹层岩柱附加围岩应力分布及其影响因素研究对于明确既有隧道变形及内力变化机理具有重要意义。基于此,本文开展重力条件下相似模型试验,对新建隧道下穿期间既有隧道应变及夹层岩柱应力变化特性开展研究,采用数值模拟的方法进一步研究夹层附加围岩应力分布以及围岩级别、下穿隧道跨度和体积损失率对附加围岩应力的影响,为新建隧道下穿既有隧道工程的设计与施工提供参考。
1 试验方案
1.1 工程背景及相似材料
模型试验以某新建高速铁路隧道小净距下穿既有重载铁路隧道工程为依托,2隧道间交叠角度为76°,新建隧道拱顶距既有隧道底部距离为16 m,上部隧道周边岩体以强风化凝灰岩为主,下部隧道周边岩体为中风化凝灰岩。2隧道均为单洞双线隧道,跨度为14 m,高度为11.8 m,模型试验中既有隧道埋深设定为10 m。
本次模型所涉及关键物理量主要有几何尺寸(),密度(),弹性模量(),应力(),应变(),泊松比(),黏聚力()和内摩擦角()。试验为1条件下模型试验,因此重力加速度()相似比为C=1:1,考虑模型试验的成本和可行性,选定几何相似比为C=1:50,密度相似比为C=1:1,根据根据Buckingham定律[18−19]确定模型相似关系(表1)。
以原型围岩力学参数为目标,选用石膏、石英砂、重晶石、铁粉、甘油和水作为原料制备围岩相似材料,经过反复配比试验,确定中风化凝灰岩原料配合比为石膏:石英砂:重晶石:铁粉:甘油:水=25:20:58:2:6:16,强风化凝灰岩原料配合比为石膏:石英砂:重晶石:铁粉:甘油:水=28:14:71:1:4:25。衬砌在特制刚性模具中进行预制,选用石膏、水泥和水作为衬砌相似材料原料。原型及相似材料物理力学参数见表2。
1.2 试验装置
根据原型尺寸、相似关系以及量测要求确定模型箱的几何尺寸。模型箱尺寸为1.6 m×1.6 m×1.6 m(图1),由高强度钢板制作而成,箱体左右两面安装有钢化玻璃,方便对试验过程进行观测。同时,在模型箱内部边界敷设光滑聚乙烯薄膜以减少箱体与围岩相似材料之间的摩擦。

表1 模型相似关系

表2 原型材料及模型相似材料物理力学参数

图1 模型箱
1.3 测试内容及试验过程
试验中对新建隧道开挖过程中夹层岩柱围岩应力和既有隧道结构应变进行了采集。压力盒共分为2组,用于采集夹层岩柱竖向围岩应力,一组位于交叉点正下方,沿深度向下布置,间距为8 cm,分别为A1~A4;另一组沿既有隧道线路方向布置于隧道底部,间距为20 cm,分别为B1~B7,其中B4与A1为同一测点;隧道下穿期间既有隧道交叉点处断面通常处于最不利受力状态[20],因此将应变监测断面布置在交叉点处,沿衬砌外表面均匀布设8组应变片,用来监测衬砌环向及纵向应变。测点布置见图2。
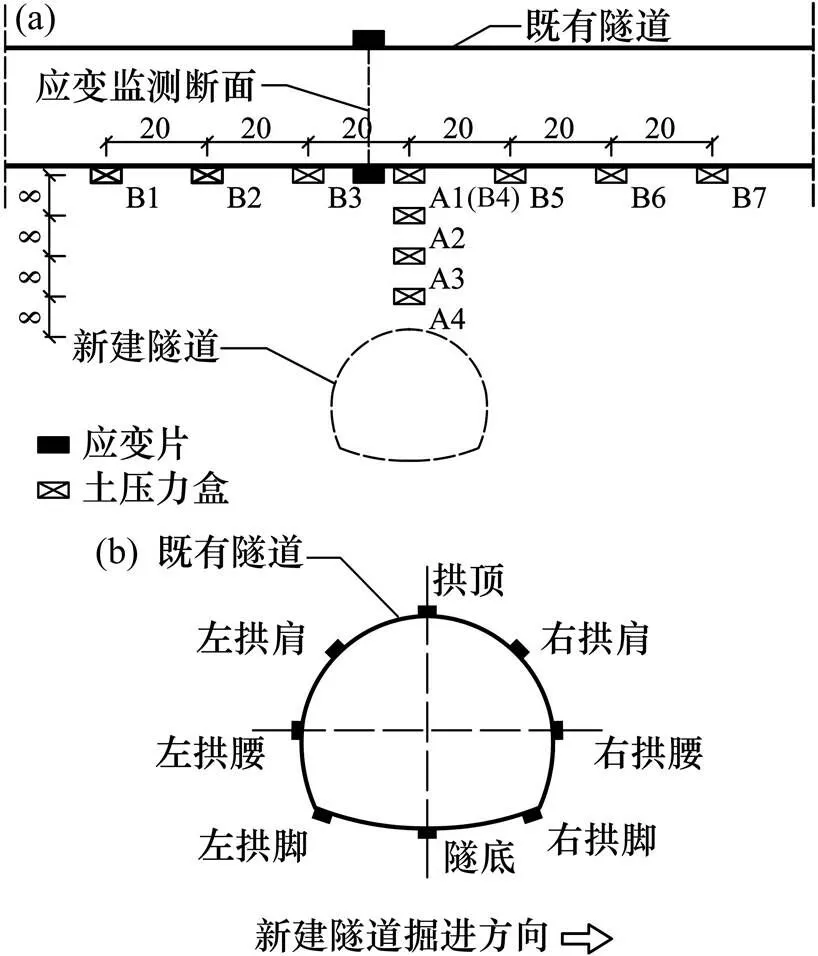
单位:cm
采用分层填筑法制备围岩,每层填筑高度5 cm,在下一层围岩填筑前进行刮毛处理,从而保证围岩材料的连续性。上部隧道衬砌预埋至隧道模型中,模型浇筑及养护完成后进行下部隧道开挖。
对于下部隧道结构,不考虑支护结构对围岩的支承作用,此时求得的围岩应力及衬砌应变相当于一种极端情况,试验结果相对于实际情况偏于安全[21−22]。下部隧道开挖长度为1.6 m,每段开挖长度为20 cm,每段开挖包括上台阶、下台阶以及落底开挖;每当完成一个开挖步,待压力盒及应变片读数稳定后,对数据进行记录,随后进行下一步的开挖。开挖方案如图3所示。

图3 开挖方案
2 试验结果分析
为便于对比与分析,将试验结果按照相似关系转换为模型对应的实际值。
2.1 附加围岩应力
围岩应力结果分析采用相对应力值,即各点开挖后围岩应力的变化值,正值表示围岩应力变大,负值代表围岩应力减小。
图4(a)为测点A1~A4附加围岩应力随新建隧道开挖变化曲线。随着新建隧道不断接近交叉点,交叉点处围岩夹层开始受到扰动,在此期间各测点围岩应力有小幅度上升;当掌子面与交叉点距离为−10~10 m范围内,新建隧道开挖导致其上方围岩松动,各测点围岩应力急剧下降;随着掌子面逐渐远离交叉点,隧道开挖的影响逐渐减弱,围岩应力趋于稳定。对比开挖前后各测点围岩应力变化值,可见随着与新建隧道垂直距离的增加,地层中附加围岩应力逐渐减小,其中,A1~A4测点围岩应力分别减小30.24,107.35,223.72和397.08 kPa。
图4(b)给出了测点B1~B7围岩应力随新建隧道开挖变化曲线。新建隧道开挖完成后,测点B3~B5(交叉点附近)围岩应力有所降低,其余测点围岩应力均有所上升。可能是因为交叉区段岩柱受到隧道开挖的影响开裂、起隙;距离交叉点一定范围外,岩体仍处于弹性变形阶段,并起到了一定承载作用,因此围岩应力升高。
2.2 既有隧道附加应变
选取4个典型开挖阶段既有隧道监测断面附加应变进行展示,如图5所示,其中拉伸应变为正,压缩应变为负。
既有隧道轴向附加应变分布见图5(a)。随着新建隧道的开挖,衬砌轴向附加应变逐渐增大,隧底、拱脚和拱腰处产生拉伸应变,拱顶及拱肩处产生压缩应变。这是由于新建隧道开挖致使上方围岩产生应力松弛现象,竖向应力急剧下降,交叉点处夹层围岩所提供的支承力也有所下降,使得既有隧道在交叉点附近沉降,进而诱发隧道结构产生轴向弯曲变形,既有隧道呈现“下凹”状态,监测断面衬砌外表面轴向附加应变表现为“上负下正”。

(a) 轴向;(b) 环向
既有隧道环向附加应变分布见图5(b)。当新建隧道距离交叉点较远时,监测断面下方岩柱受到扰动较小,因此,既有隧道产生环向附加应变较小;当掌子面推进至交叉点时,隧道附加应变呈现明显的非对称性,这主要是由于隧道左侧下方围岩开挖导致隧道左侧底部围岩应力被释放,既有隧道向左下侧偏移,致使隧道外表面环向附加应变呈现非对称分布,隧底、右拱脚、左拱肩和拱顶产生拉伸应变,其余部位为压缩应变;当隧道贯通时,监测断面左右两侧围岩应力均已释放,附加环向应变近似呈现对称分布;最终,除拱腰部位产生附加压缩应变,其余部位附加环向应变均为拉伸应变。
试验过程中,衬砌产生最大附加压缩应变为15.96 µε,远小于《混凝土结构设计规范》(GB 50010 —2010)中限值(3 300 µε);衬砌最大附加拉伸应变为35.69 µε,当衬砌初始拉伸应变值较大时,衬砌结构拉伸应变很可能会超过混凝土极限拉伸应变100~120 µε[23],此时衬砌会出现裂缝,对隧道结构防水、承载能力产生不利影响。需要指出的是,隧底及拱脚处附加拉伸应变较大,在新建隧道施工期间应重点监控,倘若衬砌出现开裂现象,应及时修补并对下穿隧道施工方案进行调整,从而保证既有隧道结构安全。
3 三维数值模拟
为深入了解隧道下穿对既有隧道的影响机制,采用数值模拟的手段对附加围岩应力在夹层中分布规律及影响因素进行分析。首先,基于模型试验参数建立三维数值分析模型,将数值计算结果与模型试验结果进行对比验证;在此基础上对附加应力在地层中的分布规律进行分析;随后设计不同工况讨论围岩级别、下穿隧道跨度和位移释放率对夹层岩柱围岩应力的影响。数值模拟方案如表3所示,其中工况1为模型试验对照工况。

表3 数值模拟方案
3.1 数值模拟参数
围岩选用服从Mohr-Coulomb屈服准则的理想弹塑性模型,衬砌结构选用线弹性模型。对于试验对照工况,依照相似关系将模型试验中隧道净距、围岩参数、交叠角度、隧道断面尺寸等参数转换为原型参数后作为数值模拟参数。其余工况在试验对照工况的基础上将交叠角度统一设定为90°,同时不考虑围岩分层特性。依照《铁路隧道设计规范》(TB1003—2005)中各级围岩物理力学参数指标,选取数值模拟工况中不同等级围岩计算参数(表4)。计算过程中对模型四周及底部边界法向位移进行约束,上表面采用自由边界。
基于体积损失法对隧道开挖进行模拟,隧道开挖后围岩会向硐室净空收敛,使得开挖空间体积产生损失,体积损失率v定义如下[24]:

式中:为单位长度围岩的损失体积;max为无支护条件下单位长度围岩的损失体积。模型试验中没有考虑支护条件,因此,在数值对照工况中体积损失率为100%。

表4 围岩物理力学参数
3.2 数值模拟与模型试验结果对比
图6对比了数值模拟和模型试验中夹层岩柱附加围岩应力。数值模拟结果和试验结果一致性较好,不仅对试验结果进行了验证,也表明采用数值模拟手段对开展夹层岩柱附加应力分布是可行的。但是需要注意的是,数值模拟和试验中附加应力分布规律还是存在着一定的差异。受到隧道开挖的影响,交叉点处沿深度方向附加应力均明显下降,并且随着与新建隧道距离的增加附加应力有所降低,但在同一深度处,由于数值模拟中岩土体为连续介质,难以反映夹层岩柱受到隧道开挖产生的开裂现象,导致交叉点处附加应力衰减幅度小于试验结果。对于既有隧道底部附加应力,二者均能反映出交叉点附近附加应力减小,远离交叉点处围岩附加应力增加这一规律,在数值模拟所得曲线中可明显看出在约±20 m存在拐点,而模型试验中该现象不明显。这可能是由试验与数值模拟边界条件的差异导致,模型试验中箱体和模型间的聚乙烯薄膜无法完全消除二者间的摩擦效应,模型箱周边岩土体和衬砌结构的位移受到限制,导致了二者在边界附近结果的偏差。

(a) A1~A4;(b) B1~B7
3.3 附加围岩应力分布
以模型试验对照工况为例,选取A1~A4所在地层附加围岩应力云图进行展示,如图7所示。图中围岩应力增加为正,减小为负。
由图7可知,新建隧道开挖会导致夹层围岩应力状态重新分布,表现为隧道正上方围岩竖向应力降低,与新建隧道水平距离超过一定范围后竖向应力增加;竖向应力下降区域随着与新建隧道距离的增加不断扩大范围,同时衰减幅度也逐渐减小,竖向应力下降区域在地层中呈现为“漏斗”状分布。新建隧道拱顶上方竖向应力衰减幅度明显高于周边竖向应力增加幅度,其中既有隧道下方附加应力低于其余部位,这主要是由于既有隧道结构承担了上部围岩传递的荷载,起到了一定的遮拦效应[14],并且距离既有隧道越远,遮拦效应越弱。
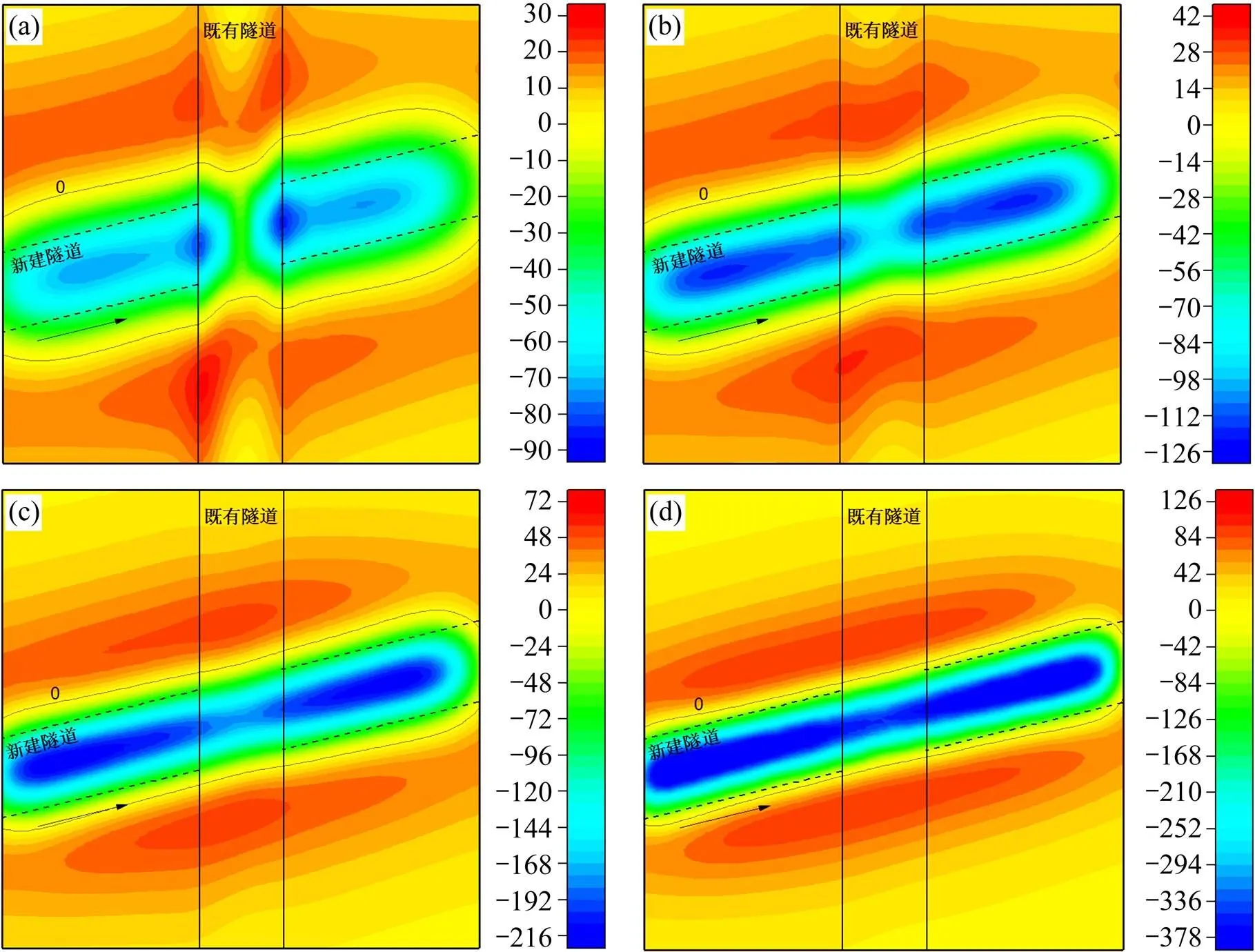
单位:kPa
3.4 附加围岩应力影响因素分析
新建隧道下穿引起围岩夹层产生的附加应力是既有隧道弯曲变形的重要因素。图8为不同围岩级别、下穿隧道跨度和体积损失率时交叉点处附加围岩应力沿深度变化曲线。
由图8(a)可知,当围岩级别从V级变为IV级和III级时,既有隧道底部竖向附加应力减少了77.8%和94.4%,说明随围岩条件的改善,隧道开挖对既有隧道的影响也逐渐减弱。随着深度的增加,围岩条件越好,附加围岩应力越大,这是由于围岩条件较好时,岩体重度相对较大,在埋深相同的部位初始竖向围岩应力也就越大,新建隧道开挖时周边应力释放程度要大于高等级围岩。与此同时,由于岩性较好,隧道压力拱边界距离新建隧道也就越近,夹层岩柱中受影响范围也有所减小,既有隧道底部附加围岩应力也相对较小。
由图8(b)可知,当隧道跨度减小时,新建隧道开挖引起周边应力释放程度会有所降低,对既有隧道的影响也会减小。其中,当跨度由14 m减小到 7 m时,深度14 m处围岩应力减少34.7%,深度0 m处围岩应力减少27.0%。同时可以发现,附加围岩随新建隧道跨度的变化并非呈现线性关系,跨度由14 m减小到10.5 m时地层附加围岩应力减小幅度明显低于跨度由10.5 m减小到7 m的情况。
由图8(c)可知,围岩夹层中附加围岩应力随着体积损失率的减小而逐渐降低。隧道开挖是一个体积释放及应力释放的过程,隧道开挖引起周边地层位移,最终在围岩及支护结构的作用下趋于稳定。同时,隧道开挖也引起地层中初始应力的释放,所释放的应力则由围岩以及支护结构承担,二者基本成线性关系[25]。控制新建隧道体积损失率能够减小隧道开挖引起的应力释放现象,对既有隧道的扰动也会有所降低。因此,对于新建隧道下穿既有隧道工程,尤其是大断面、小净距下穿的情况,下部隧道支护结构应及时施做,并尽早闭合,限制夹层岩柱的松动变形,避免围岩应力大量释放,造成既有隧道产生超量附加应变。
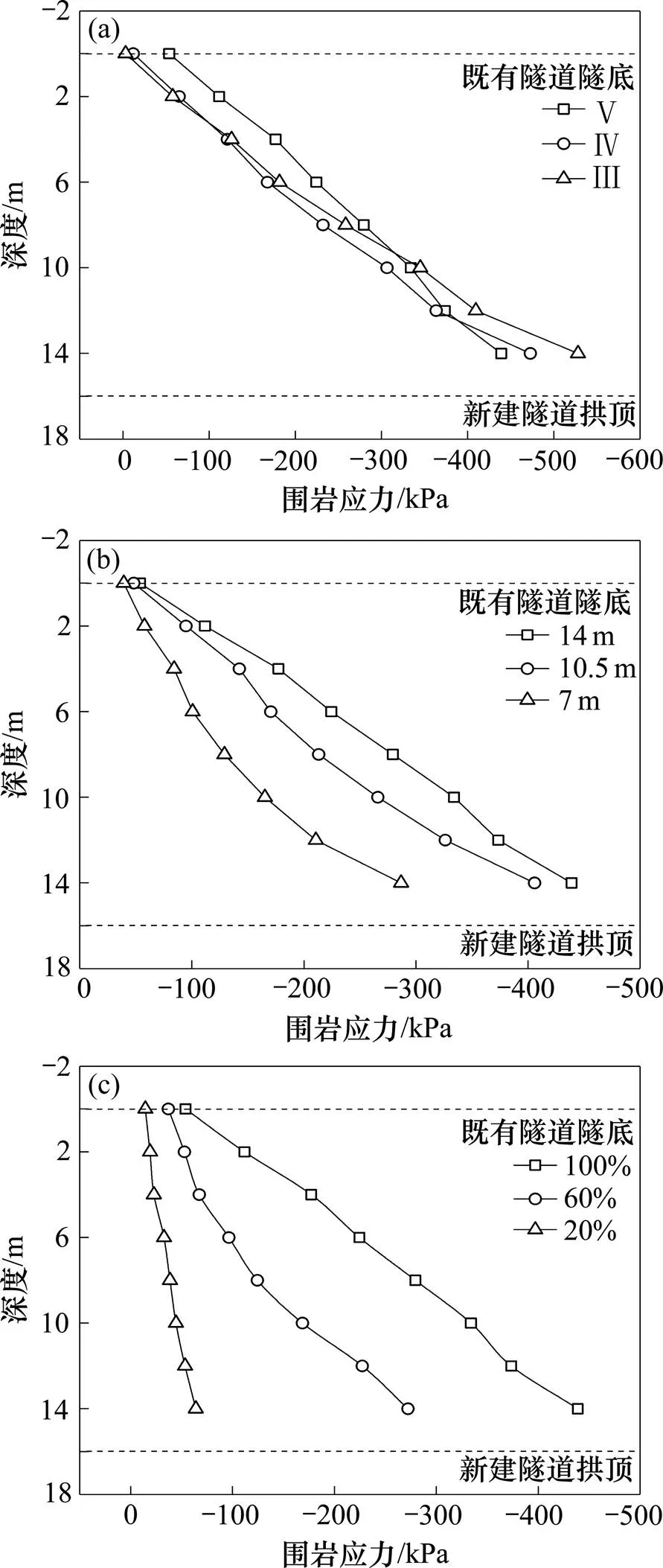
(a) 围岩级别;(b) 下穿隧道跨度;(c) 体积损失率
4 结论
1) 受到下穿隧道开挖的影响,交叉点处夹层岩柱中围岩应力急剧下降,距离新建隧道越近围岩应力减小幅度越大。对于既有隧道底部与围岩接触应力,交叉点附近围岩应力下降,远离交叉点的部分围岩应力有所上升。
2) 既有隧道轴向附加应变为“上负下正”,隧道沿轴向呈现“下凹”状态。既有隧道隧底附加拉应变最大,施工期间应对隧道基底受力状态重点监控。
3) 数值计算基本能够反映隧道开挖期间夹层岩柱围岩应力变化。新建隧道上方围岩应力下降区域在地层中呈“漏斗”状分布,距离新建隧道垂直距离越远围岩应力下降区域越大并且衰减幅度越小;其中,由于既有隧道的遮拦效应,交叉点处附加围岩应力明显低于其他部位。
4) 随围岩条件的改善,隧道开挖对既有隧道的影响逐渐减弱;新建隧道跨度和体积损失率减小均会使得夹层中附加围岩应力减小。对于新建隧道下穿既有隧道工程,宜及时采取支护措施以控制新建隧道结构变形,避免围岩应力大量释放,以减少对既有隧道的影响。
本文试验及数值模拟设定的条件为浅埋交叉隧道,当隧道埋深增加时围岩应力状态会发生显著变化,结论在深埋交叉隧道中的适用性需要进一步验证。
[1] 梁荣柱, 宗梦繁, 康成, 等. 考虑隧道剪切效应的隧道下穿对既有盾构隧道的纵向影响[J]. 浙江大学学报(工学版), 2018, 52(3): 420−430. LIANG Rongzhu, ZONG Mengfan, KANG Cheng, et al. Longitudinal impacts of existing shield tunnel due to down-crossing tunnelling considering shield tunnel shearing effect[J]. Journal of Zhejiang University (Engineering Science), 2018, 52(3): 420−430.
[2] 李玉峰, 彭立敏, 雷明锋. 交叉隧道工程设计施工技术研究进展[J]. 铁道科学与工程学报, 2014, 11(1): 67−73. LI Yufeng, PENG Limin, LEI Mingfeng. Research progress in the design and construction technology of crossing tunnels[J]. Journal of Railway Science and Engineering, 2014, 11(1): 67−73.
[3] 张桓, 张子新. 盾构隧道开挖引起既有管线的竖向变形[J]. 同济大学学报(自然科学版), 2013, 41(8): 1172− 1178. ZHANG Huan, ZHANG Zixin. Vertical deflection of existing pipeline due to shield tunnelling[J]. Journal of Tongji University (Natural Science), 2013, 41(8): 1172− 1178.
[4] Klar A, Vorster T E B, Soga K, et al. Soil-pipe interaction due to tunnelling: comparison between Winkler and elastic continuum solutions[J]. Geotechnique, 2005, 55(6): 461−466.
[5] LIU X, FANG Q, ZHANG D L. Mechanical responses of existing tunnel due to new tunnelling below without clearance[J]. Tunnelling and Underground Space Technology, 2018, 80: 44−52.
[6] 张冬梅, 宗翔, 黄宏伟. 盾构隧道掘进引起上方已建隧道的纵向变形研究[J]. 岩土力学, 2014, 35(9): 2659− 2666. ZHANG Dongmei, ZONG Xiang, HUANG Hongwei. Longitudinal deformation of existing tunnel due to underlying shield tunneling[J]. Rock and Soil Mechanics, 2014, 35(9): 2659−2666.
[7] Ng C W W, Fong K Y, LIU H L. The effects of existing horseshoe-shaped tunnel sizes on circular crossing tunnel interactions: Three-dimensional numerical analyses[J]. Tunnelling and Underground Space Technology, 2018, 77: 68−79.
[8] Avgerinos V, Potts D M, Standing J R. Numerical investigation of the effects of tunnelling on existing tunnels[J]. Geotechnique, 2017, 67(9): 808−822.
[9] 林越翔, 彭立敏, 施成华, 等. 盾构下穿施工对既有隧道管片接头力学性能影响机制研究[J]. 铁道科学与工程学报, 2017, 14(8): 1698−1706. LIN Yuexiang, PENG Limin, SHI Chenghua, et al. Static-dynamic character about segment joint of existing shield tunnel under the influence of under-cross tunnel construction using shield tunnelling[J]. Journal of Railway Science and Engineering, 2017, 14(8): 1698− 1706.
[10] 来弘鹏, 郑海伟, 何秋敏, 等. 砂土地层盾构隧道小角度斜下穿既有隧道施工参数优化研究[J]. 中国公路学报, 2018, 31(10): 130−140. LAI Hongpeng, ZHENG Haiwei, HE Qiumin, et al. Investigation into parameter optimization of existing metro tunnel for shield tunnel closely undercrossing it at small angle sand stratum[J]. China Journal of Highway and Transport, 2018, 31(10): 130−140.
[11] 李玉峰, 雷明锋, 鲁贵卿, 等. 不同因素对立体交叉隧道施工的影响规律分析[J]. 现代隧道技术, 2014, 51(1): 117−123. LI Yufeng, LEI Mingfeng, LU Guiqing, et al. Analysis of factors affecting intersected tunnel construction[J]. Modern Tunnelling Technology, 2014, 51(1): 117−123.
[12] Ng C W W, Wang R, Boonyarak T. A comparative study of the different responses of circular and horseshoe- shaped tunnels to an advancing tunnel underneath[J]. Geotechnique Letters, 2016, 6(2): 168−175.
[13] Ng C W W, Boonyarak T, Masin D. Three-dimensional centrifuge and numerical modeling of the interaction between perpendicularly crossing tunnels[J]. Canadian Geotechnical Journal, 2013, 50(9): 935−946.
[14] MA S K, LIU Y, LÜ X L, et al. Settlement and load transfer mechanism of pipeline due to twin stacked tunneling with different construction sequences[J]. Ksce Journal of Civil Engineering, 2018, 22(10): 3810−3817.
[15] 张晓清, 张孟喜, 李林, 等. 多线叠交盾构隧道近距离穿越施工扰动机制研究[J]. 岩土力学, 2017, 38(4): 1133−1140. ZHANG Xiaoqing, ZHANG Mengxi, LI Lin, et al. Mechanism of approaching construction disturbance caused by multi-line overlapped shield tunnelling[J]. Rock and Soil Mechanics, 2017, 38(4): 1133−1140.
[16] 孙振宇, 张顶立, 房倩, 等. 浅埋小净距公路隧道围岩压力分布规律[J]. 中国公路学报, 2018, 31(9): 88−98. SUN Zhenyu, ZHANG Dingli, FANG Qian, et al. Distribution of surrounding rock pressure of shallow highway tunnels with small spacing[J]. China Journal of Highway and Transport, 2018, 31(9): 88−98.
[17] 唐陶文, 傅鹤林, 张加兵, 等. 分岔隧道中夹岩柱围岩应力及最小厚度研究[J]. 铁道科学与工程学报, 2016, 13(8): 1578−1584. TANG Taowen, FU Helin, ZHANG Jiabing, et al. Research on surrounding rock pressure and minimum thickness of middle rocky column in the branched tunnel[J]. Journal of Railway Science and Engineering, 2016, 13(8): 1578−1584.
[18] FANG Y, XU C, CUI G, et al. Scale model test of highway tunnel construction underlying mined-out thin coal seam[J]. Tunnelling and Underground Space Technology, 2016, 56: 105−116.
[19] Carpinteri A, Chiaia B. Power scaling laws and dimensional transitions in solid mechanics[J]. Chaos Solitons and Fractals, 1996, 7(9): 1343−1364.
[20] 龚伦. 上下交叉隧道近接施工力学原理及对策研究[D]. 成都: 西南交通大学, 2008. GONG Lun. Study on mechanics principle and countermeasures of adjacent excavation in up-down cross tunnels[D]. Chengdu: Southwest Jiaotong University, 2008.
[21] 黄锋, 朱合华, 徐前卫. 含软弱夹层隧道围岩松动破坏模型试验与分析[J]. 岩石力学与工程学报, 2016, 35(增1): 2915−2924. HUANG Feng, ZHU Hehua, XU Qianwei. Model test and analysis about loose failure of tunnel surrounding rock mass containing weak interlayer[J]. Chinese Journal of Rock Mechanics and Engineering, 2016, 35(Suppl 1): 2915−2924.
[22] 白浪峰, 徐前卫, 田龙岗, 等. 软弱破碎连拱隧道松动区模型试验与分析[J]. 岩石力学与工程学报, 2013, 32(增2): 3610−3618. BAI Langfeng, XU Qianwei, TIAN Longgang, et al. Model test and analysis of loose zone in soft and cracked surrounding rock of multi-arch tunnel[J]. Chinese Journal of Rock Mechanics and Engineering, 2013, 32(Suppl 2): 3610−3618.
[23] 王千星, 杨维好, 王衍森. 厚表土斜井冻结凿井期井壁混凝土应变实测研究[J]. 采矿与安全工程学报, 2016, 33(4): 655−661. WANG Qianxing, YANG Weihao, WANG Yansen. Study on concrete strain of inclined shaft lining in deep alluvium during freezing sinking period[J]. Journal of Mining & Safety Engineering, 2016, 33(4): 655−661.
[24] 杨友彬, 郑俊杰, 赖汉江, 等. 一种改进的隧道开挖应力释放率确定方法[J]. 岩石力学与工程学报, 2015, 34(11): 2251−2257. YANG Youbin, ZHENG Junjie, LAI Hanjiang, et al. A revised method for calculationg stress release ratio in tunnel excavation[J]. Chinese Journal of Rock Mechanics and Engineering, 2015, 34(11): 2251−2257.
[25] 郭瑞, 方勇, 何川. 隧道开挖过程中应力释放及位移释放的相关关系研究[J]. 铁道工程学报, 2010, 27(9): 46− 50. GUO Rui, FANG Yong, HE Chuan. Study of the correlation between stress release and displacement release during tunnel excavation[J]. Journal of Railway Engeering Society, 2010, 27(9): 46−50.
Influence of under-crossing on the rock stress of pillar between crossing tunnels
DONG Jie1, 2, ZHONG Shuai1, 2
(1. Hebei University of Architecture, Zhangjiakou 075000, China; 2. Hebei Key Laboratory for Diagnosis, Reconstruction and Anti-disaster of Civil Engineering, Zhangjiakou 075000, China)
A similar model experiment under gravity conditions was carried out to research the variation law of rock stress and its influencing factors in the interlayer rock pillar. The additional stress of interlayer rock pillar and the induced strain of the existing tunnel lining during the excavation of new tunnel were collected, and correspondingly numerical calculation was carried out. The results show that the rock stress of the interlayer rock pillar at the intersection decreases drastically after the completion of the new tunnel excavation. The existing tunnel is bent downward along its axis under the influence of the lower tunnel excavation. Due to the successive release of rock stress on both sides of the strain monitoring section, the additional hoop strain gradually changes from asymmetric distribution to symmetric distribution. And the decreased surrounding rock stress in the interlayer rock pillar has a funnel-shaped distribution. The shielding effect of the existing tunnel makes the surrounding rock stress at the intersection less than other parts. When the rock condition is good, the induced rock stress at the bottom of the tunnel is small. With the decrease of the span and volume loss rate of the new tunnel, the additional surrounding rock stress in the stratum decreases gradually.
crossing tunnel; rock stress; model experiment; numerical calculation
U25
A
1672 − 7029(2020)04 − 0947 − 10
10.19713/j.cnki.43−1423/u.T20190588
2019−06−30
国家自然科学基金资助项目(51878242);河北省高等学校科学技术研究重点项目(ZD2018244);河北省人才工程培养资助项目(A201901067)
董捷(1980−),男,河北张家口人,教授,博士,从事交通工程防灾减灾研究;E−mail:493564550@qq.com
(编辑 阳丽霞)
——以渤海A 油藏为例

