用圆处理张角问题
2020-05-03 13:19叶文明叶丽英
高中数学教与学 2020年5期
叶文明 叶丽英
(浙江省松阳县第二中学,323406)
圆是一种常见的图形,其中蕴含着丰富的几何性质,许多数学问题都以它为背景进行设计,是命题人比较青睐的素材.比如,圆周角定理是圆的一个重要性质,再结合三角形的性质,我们不难得到圆周角大于圆外角,且圆周角小于圆内角.本文举例说明以此为背景设计的一类最值或取值范围问题,根据张角的上述性质可以使问题简便获解.
例1已知点A(1,0)、B(2,0),动点P是直线x=7y上任意一点,则∠APB的最大值为( )
(A)90° (B)120° (C)135° (D)150°
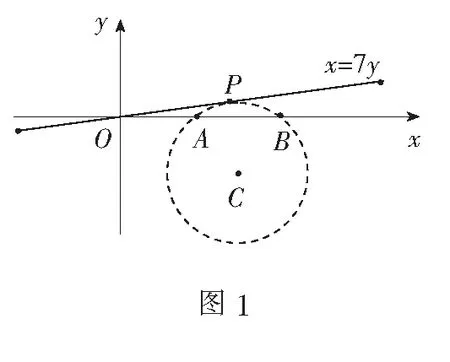
分析考察以AB为弦且与直线x=7y相切的定圆,则点P为切点时∠APB最大.
解如图1,依题意,可设以AB为弦且与
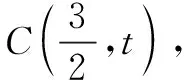

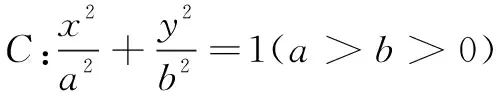
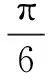

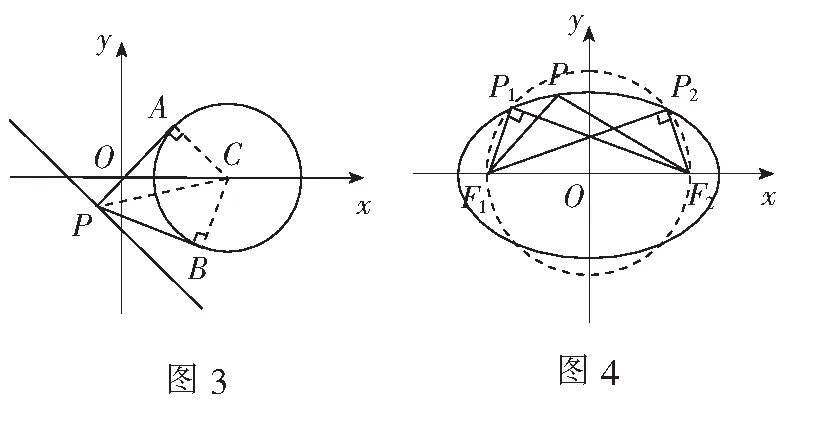
例2已知P是直线2x+2y+3=0上任意一点,过点P作圆C:(x-a)2+y2=1(a>0) 的两切线PA、PB,切点分别为A、B.若∠APB恒为锐角,则实数a的取值范围为______.


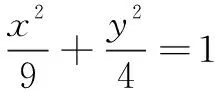
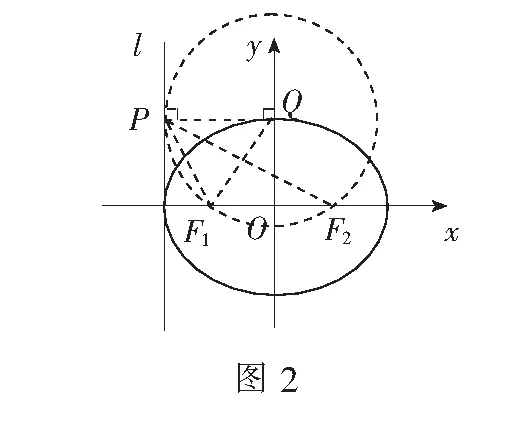
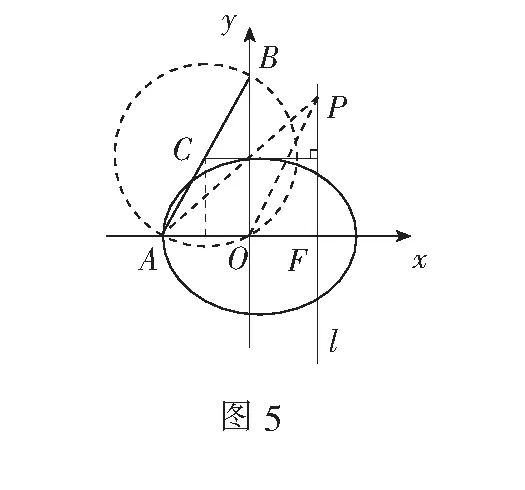
解如图4,以F1F2为直径作圆与椭圆交于P1、P2,则∠F1P1F2=∠F1P2F2=90°. 由圆内角大于圆周角可知当点P位于点P1、P2之间时,∠F1PF2为钝角.
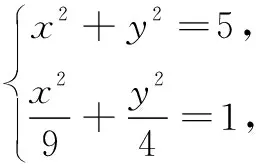



猜你喜欢
小学生优秀作文(高年级)(2022年3期)2022-03-29
小学生学习指导(中年级)(2021年4期)2021-04-27
中学生数理化·中考版(2020年11期)2020-12-14
初中生学习指导·提升版(2020年12期)2020-09-10
中学数学杂志(初中版)(2019年4期)2019-09-18
读书文摘(下半月)(2019年12期)2019-09-10
广东教育·高中(2018年12期)2018-02-13
初中生世界·九年级(2017年9期)2017-10-13
初中生世界(2017年9期)2017-03-04
下一代英才(2016年4期)2016-11-19

