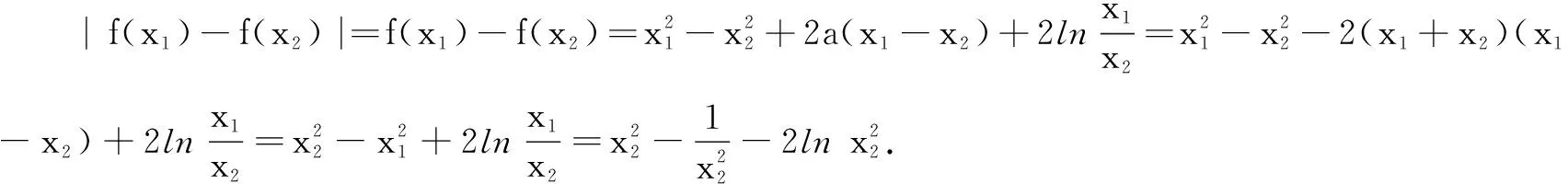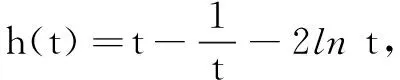高三数学综合测试

一、填空题(本大题共有14小题,每小题5分，计70分)

3.底面半径为1,母线长为3的圆锥的体积是______.

4.在三张奖券中有一、二等奖各一张,另一张无奖.甲、乙两人各抽取一张(不放回),两人都中奖的概率为______.

5.根据如图所示的伪代码,已知输出值y为3,则输入值x为______.

Readx

Ifx≥0 Then

y←sinx

Else

y←x2-1

End If

Prindy

6.已知样本6,7,8,9,m的平均数是8,则方差是______.

10.已知正实数x、y满足x+4y-xy=0,若x+y≥m恒成立,则实数m的取值范围为______.

12.设实数x、y满足x2+2xy-1=0,则x2+y2的最小值是______.

二、解答题(本大题共6小题,计90分.解答时应写出必要的文字说明、证明过程或演算步骤)

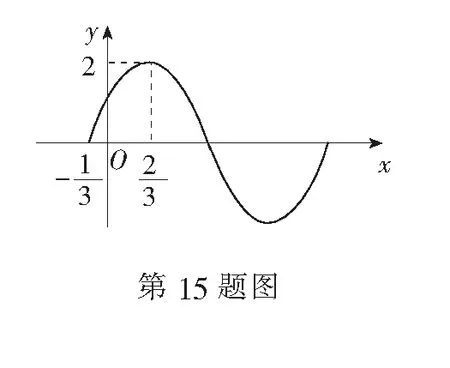
(1)求函数f(x)的解析式;

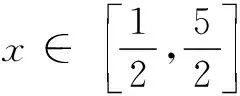
16.(本小题满分14分)如图,在正三棱柱ABC-A1B1C1中,E、F分别为BB1、AC的中点.求证:

(1)BF∥平面A1EC;

(2)平面A1EC⊥平面ACC1A1.

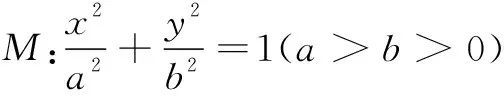
(1)求椭圆的离心率;

(2)若y轴被∆ABC的外接圆所截得的弦长为9,求椭圆的方程.

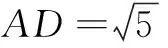
(2)当草坪ABCD的面积最大时,求此时小路BD的长度.

19.(本小题满分16分)在数列{an}中,已知a1=1,a2=a,且an+1=k(an+an+2)对任意正整数n都成立,数列{an}的前n项和为Sn.

(2)是否存在实数k,使数列{an}是公比不为1的等比数列,且对任意相邻三项am、am+1、am+2按某顺序排列后成等差数列?若存在,求出所有k的值;若不存在,请说明理由;

20.(本小题满分16分)已知函数f(x)=(3-x)ex,g(x)=x+a(a∈R)(e是自然对数的底数,e≈2.718…).

(1)求函数f(x)的极值;

(2)若函数y=f(x)g(x)在区间[1,2]上单调递增,求a的取值范围;

参考答案

一、填空题

二、解答题

16.(1) 连结AC1交A1C于点O,连结OE、OF.

在正三棱柱ABC-A1B1C1中,四边形ACC1A1为平行四边形,所以OA=OC1.

又BF⊄平面A1EC,OE⊂平面A1EC,所以，BF∥平面A1EC.

(2)因为AB=CB,点F为AC的中点,所以BF⊥AC.由(1)知BF∥OE,所以OE⊥AC.

因为AA1⊥底面ABC,而BF⊂底面ABC,所以AA1⊥BF.

由BF∥OE,得OE⊥AA1,而AA1、AC⊂平面ACC1A1,且AA1∩AC=A,所以OE⊥平面ACC1A1.因为OE⊂平面A1EC,所以平面A1EC⊥平面ACC1A1.

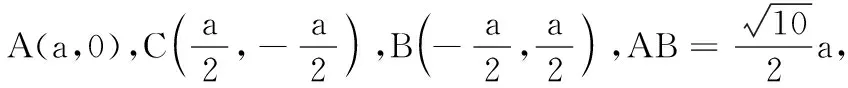
SABCD=S∆ABD+S∆BCD

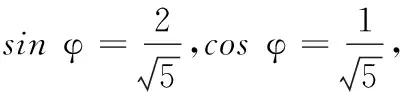
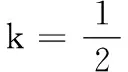
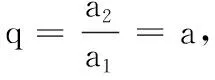
若am+1为等差中项,则2am+1=am+am+2,即2am=am-1+am+1,解得a=1,不合题意.

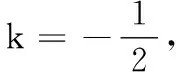
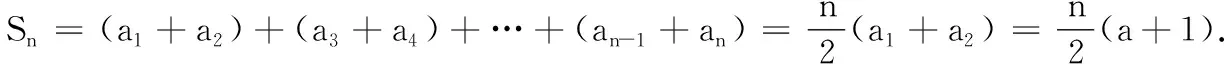
n=1时上式也成立.

20.(1)f(x)=(3-x)ex，f′(x)=(2-x)ex，令f′(x)=0，解得x=2.

易见x∈(-∞,2)时，f′(x)>0,f(x)单调增；x∈(2,+∞)时，f′(x)<0,f(x)单调减.

故当x=2时，函数f(x)取得极大值f(2)=e2，无极小值.

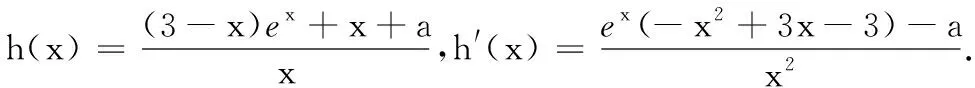
r′(x)=x(1-x)ex,当x∈(0,1)时，r′(x)>0,r(x)单调增；当x∈(1,+∞)时，r′(x)<0,r(x)单调减.

由h′(x2)=0,得a=ex2(-x22+3x2-3)，故

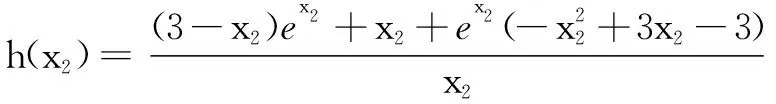
令H(x)=ex(2-x)，则H′(x)=ex(1-x),当x∈(1,+∞)时，H′(x)<0,H(x)单调减.

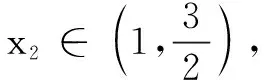
由h(x)的极小值小于整数b,可知满足题意的整数b的最小值为4.

(2)若f(x)存在两个极值点x1、x2,且x2≥e,|f(x1)-f(x2)|≥m恒成立,求m的最大值．

解(1)略.

(2)依题意，x1、x2是方程x2+ax+1=0的两根，故x1+x2=-a,x1x2=1.