有趣的零点存在定理
秦志伟
(江苏省天一中学,214101)
我们教师在教学过程中常常会遇到一种情形:一些看似显然的结果,但很难说清它的理由.比如“极限”的概念,我们教师更多的是让学生去直观感受,很少会用大学的“ε-δ”分析的语言来加以说明.尽管在初等数学的范围里确实很难把一些问题讲得透彻,但这并不意味着我们就能放弃这种努力.数学是讲究理性精神的,而教学也应当进行潜移默化的影响.当我们放弃这种努力的同时也几乎丢掉了数学的精神.在本文中,笔者分享自己亲历的两个情形,尝试践行数学的理性精神.
一、问题的提出

在解决该题时,学生给出了如下两种解题思路.

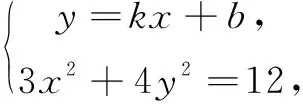
(3+4k2)x2+8kbx+4b2-12=0.
(*)
由(*)式中Δ>0,得b2<3+4k2.

(**)

反思1两种方法的答案一致.解法1比较常规;解法2利用了点差法,过程比较简洁.问题来了,解法2中,xM的范围真的是(-2,2)吗?换言之,椭圆内部的任一点,都有可能成为椭圆某一条弦的中点吗?

学生对该题的解答如下.
解考虑两个极端情况:
情况1,若动点选定方向后再也不改变方向,则动点的终点轨迹为圆弧AB(其中圆弧半径为20米);情况2,若动点先沿正东方向行走若干时间后再沿正北方向行走,则动点的终点轨迹为线段AB(如图2).故大胆地猜测,动点的终点所有可能的落点区域为弓形区域AB,故不难求得此区域面积为(100π-200)平方米.

反思2学生的这个想法非常大胆,但同样有个问题:弓形内部的任一点都有可能成为某一种符合要求的路径的终点吗?
二、问题的解决
以上两个问题的答案都是肯定的,其结果符合我们对事物的认知,但又缺乏严密的说理.事实上,在高中课程内,我们是可以将其说得更清楚的.利用的工具就是函数章节中的零点存在定理——若函数y=f(x)在区间[a,b]上的图象是一条不间断的曲线,且f(a)f(b)<0,则函数y=f(x)在区间(a,b)上有零点.
下面对两个案例中的问题加以说明.
1.案例1中问题的说明

2.案例2中问题的说明


三、问题的反思
笔者引入零点存在定理,解决了案例1、2中的问题后,学生惊叹不已.事实上,变化的过程往往可以建立一个函数的模型,连续不断地变化,意味着函数图象的不间断.零点存在定理告诉我们,事物由一种状态连续地变化至另一种状态的过程中,必然达到中间的所有状态.
趁学生意犹未尽时,笔者适时地给出两个练习,现把学生的解答附上,供读者参考.
练习1在地球的赤道上,至少存在一对对径点,在这两点处的温度相同.

解在赤道上任取一组对径点的连线AB作为x轴(如图5),其他对径点的连线MN与x轴的夹角为θ,θ∈(0,π).定义函数f(θ)的值为点M处的温度与点N处的温度之差.若A、B两点温度一样,则点A、B符合要求;否则,由f(0)=-f(π)知,必有f(0)f(π)<0,根据零点存在定理知,存在θ0∈(0,π),使f(θ0)=0,即存在一对对径点,在这两点处的温度相同.
练习2某人第一天在早上8点到9点的时间段从山脚A处走到山顶B处,第二天此人在早上8点到9点的时间段从山顶B处原路返回至山脚A处,那么,在早上8点到9点的时间段,必定存在某一时刻,第一天与第二天的位置相同.
解不妨设A处与B处的落差为h(h>0),设8点之后的t分钟,第一天的位置高度为f(t),第二天的位置高度为g(t),其中t∈[0,60].令F(t)=f(t)-g(t),显然F(0)=f(0)-g(0)=-h<0,F(60)=f(60)-g(60)=h>0.由于F(t)的连续性,由零点存在定理知,存在t0∈(0,60),使得F(t0)=0.又因为是原路返回,故当第一天和第二天所处位置的高度一致时,就意味着位置的重叠,所以必定存在某一时刻8点过后t0分钟,第一天与第二天的位置相同.
尽管零点存在定理是函数章节中的知识,但是它揭示了变化事物的本质属性.而事物的变化本身就是一个函数的模型.我们教师在平时的教学中也不应局限于泾渭分明的模块教学,如果模块之间提供了相互佐证的机会,我们应该不失时机地利用它.这个过程是有趣的,它加强了学生对知识本身的理解和应用,提高了学生学习的兴趣;同时这个过程也具有挑战性,它践行了数学理性的精神,增加了学科的魅力.

