混合指数跳扩散模型下基于FST方法的期权定价

张素梅, 赵洁琼

(西安邮电大学理学院，西安 710121)

1 引言

在期权定价中，基于布朗运动和正态分布建立的BS 模型[1]假设过于理想化，无法解释资产收益的尖峰厚尾和波动率“微笑”现象.为了解释这些现象，1976 年，Merton[2]提出log 正态跳扩散模型，该模型可以解释资产收益的尖峰厚尾和波动率“微笑”现象，具有开创性意义.随后在2002 年，Kou 提出双指数跳扩散模型[3]，其跳跃过程服从双指数分布.并且相对于log 正态跳扩散模型，该模型更易于求出路径期权的封闭解析定价公式.2007 年，Kou 和Cai 将双指数跳扩散模型的概率密度函数扩展到有限次数的上跳和下跳，由此推出超指数跳扩散模型[4]，其跳跃过程服从超指数分布.然而，上述这些模型只能解决特定的分布问题，在实际金融市场的应用中具有很大的局限性.所以在2011 年，Kou 和Cai 提出混合指数跳扩散模型(Mixed-Exponential Jump Diffusion Model, MEM)[5]，该模型跳跃过程服从混合指数分布，而混合指数分布是指数分布的加权平均值，其权重可以为负.根据这一特征，该分布可以逼近为任何分布，其中包括正态分布、各种指数分布以及像Gamma, Weibull 和Pareto 所产生的厚尾分布等，具有一般性，可以广泛应用于刻画股价实际变动趋势.

为了方便解决实际问题，对于模型来说，求解其期权定价一直以来都是重中之重.然而由于跳扩散模型包含跳跃过程，所以很难通过理论方法得到一个完整的闭式解析式，在实际求解中通常采用数值方法对期权进行定价.目前常用的数值计算方法有二叉树、有限差分、Monte Carlo(MC)、快速傅里叶变换(Fast Fourier Transform, FFT)和双边欧拉反演(Euler inversion, EI or BA) 法等等.上述五种方法中，二叉树方法[6]由于数学原理简单且易操作，成为广泛应用的期权定价方法之一.但是对于复杂的跳扩散模型，节点的增多会导致二叉树方法收敛速度过慢.有限差分方法[6]同样由于原理简单而被广泛应用于期权定价，但是对于跳扩散模型所产生的偏积分-微分方程(partial-integro differential equation, PIDE)的积分项进行求解时，需要进行相关近似，使得方法相当复杂，且在求解过程中容易出现准确性差和收敛速度慢的问题.MC 方法[7]在求解期权定价时方便操作，并适用于高维期权定价的求解，通常被用于计算期权定价的数值解[8-10]，但是由于MC 方法模拟次数多，运行时间长，很少用于欧式期权定价的求解.Carr 在1999 年使用FFT 方法[11]求解期权定价的数值解，大大提高了期权定价的运算速度，并且易于实施，被广泛地应用于计算跳扩散模型下期权定价的数值解[12-14]，不过FFT 方法的精度与阻尼因子的选取有关，所以数值结果不稳定.2004 年Petrella 提出的BA 方法[15]主要是通过拉普拉斯变换的相关性质进行求解，该方法因其高效、快速的优点被用于超指数模型和混合指数模型的数值求解[4,5,16]，但其推导过程复杂.而本文所采用的FST 方法[17,18]利用傅里叶变换将PIDE 从时域转换到频域.直接在频域中求解的优点是含有独立增量的随机过程通过傅里叶变换将特征指数从PIDE 中分解出来，从而获得易于求解的常微分方程(Ordinary Differential Equation, ODE).这使得期权定价的求解只与特征指数有关，减少了运算量.并且对于任何指数型Lvy 过程，FST 方法具有通用性，即只需要得到特征指数的解析式即可.

本文将FST 方法和MEM 相结合，主要有两点创新：一是将FST 方法推广到MEM 下的欧式期权定价；二是首次将MEM 校正到实际市场，并探寻了跳参数对于隐含波动率的影响.文章的具体结构如下：第2 章给出了MEM 的基本假设，并推导出MEM 的期权定价所符合的PIDE；第3 章给出使用FST 方法对于MEM 下欧式期权定价求解的详细推导过程；第4 章进行FST 方法与其它数值方法的数值模拟；第5 章进行模型校正；第6 章总结全文.

2 混合指数跳扩散模型

在概率测度P 下，假设资产价格过程St满足如下MEM

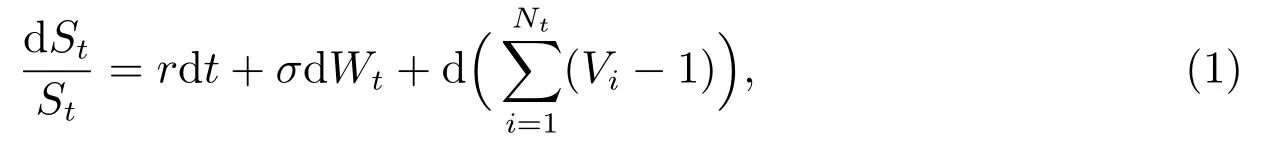
其中r为无风险利率，Wt是标准布朗运动，Nt是强度为λ的泊松过程，Yi= ln(Vi)是混合指数随机变量，其概率密度函数fY(x)为

上式pu ≥0,qd= 1-pu ≥0，其中pi ∈(-∞,∞),ηi ＞1,i= 1,2,···,m,qj ∈(-∞,∞),θj ＞0,j= 1,2,···,n.分别表示上跳和下跳的概率及跳跃值.由公式(2)可知，跳跃包括m类上跳和n类下跳，第i类上跳的概率为pi，第j类下跳的概率为qj，且

根据pi和qj的参数范围可知其可以为负数，所以要保证概率密度函数fY(x)总是非负函数，上述参数就需要满足以下充分必要条件：其中必要条件为p1＞0,q1＞充分条件为对于所有的k= 1,2,···,m和l=1,2,···,n，有

设过程Wt,Nt及随机变量Vi相互独立.易见：(I) 当pi和qj为非负参数时，模型(1)为超指数跳扩散模型；(II) 当m= 1,n= 1 时，模型(1)为双指数跳扩散模型；(III) 当λ=0 时，模型(1)为BS 模型.

由上述公式(1)和(2)可知，当St发生跳跃时，[St]=St+-St= (Vi- 1)St，即St+=St((Vi-1)+1)=StVi.

令Xt= ln(St)，则Xt+= lnSt+= lnSt+lnVi= lnSt+Yi，故由 It公式，公式(1)可改写为

在风险中性测度Q 下，过程dSt和dXt分别为

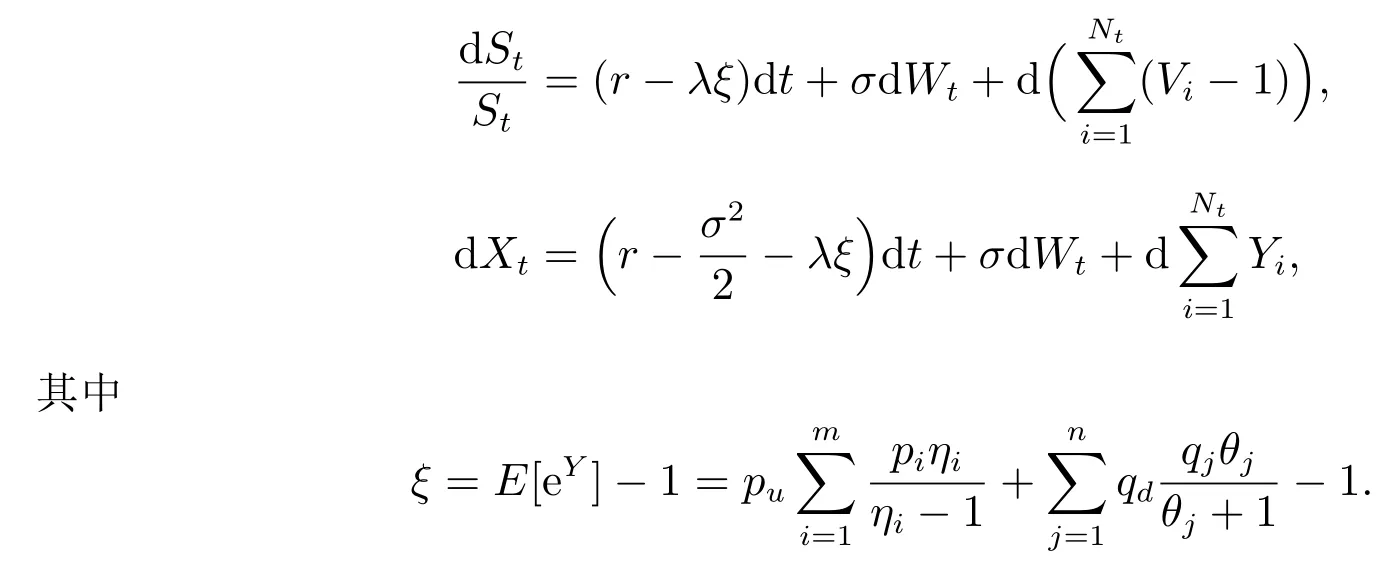
定理1(Lvy 过程的特征函数)[19]若Xt是Rd上一个Lvy 过程，则存在一个连续函数ψ为X 的特征指数，则

证明 证明见文献[19].

根据定理1，通过直接计算可知，MEM 的特征函数为

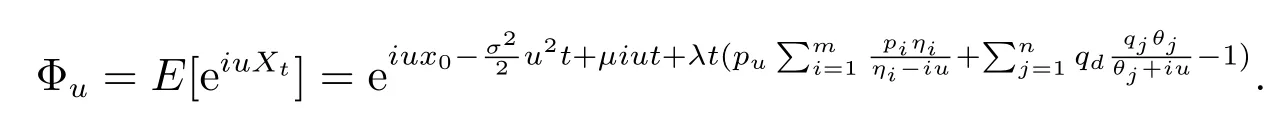
特征指数ψ(u)为

定理2(Lvy-Khinchine公式)[19]若Xt是Rd上包含三个参数 (γ,A,ν)的一个 Lvy 过程，对满足E[exp(iz.Xt)]=exp(tψ(z))的ψ(z)有Lvy-Khinchine 公式

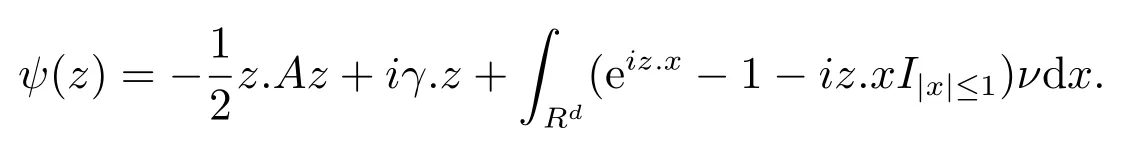
其中νdx=λfY(x)dx.

证明 证明见文献[19].

定理3(跳扩散中的It公式)[19]令X是一个带跳跃的扩散过程，其跳跃过程为一复合泊松过程

其中bt以及σt是连续不可预测过程满足：在任意时间[0,T]上，存在函数f:[0,T]×R →R，过程Yt=f(t,Xt)满足如下微分形式

证明 证明见文献[19].

设V=V(St,t)是期权价格，在到期日t=T时的看涨期权为V(St,t) = (S-K)+，K为敲定价格.期权t时刻价格为v(Xt,t) =V(S0eXt,t)，其中St=S0eXt.根据定理2 和定理3 可知MEM 符合下列PIDE

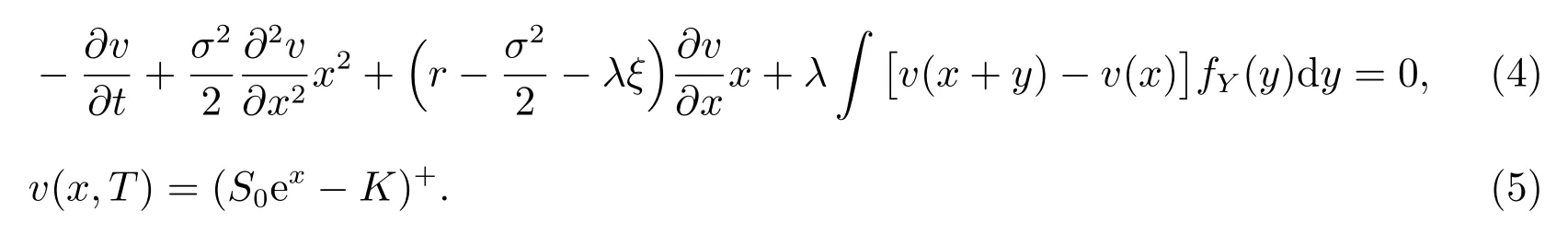
3 混合指数跳扩散模型下欧式期权定价的FST 方法

FST 方法是将期权定价满足的PIDE 转换到频域，再通过傅里叶逆变换转换回时域.下面以看涨期权为例，给出MEM 下欧式期权定价的FST 方法的详细推导过程.

对于公式(4)形式的PIDE，进行连续傅里叶变换F得

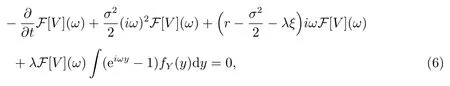
上式中变量ω表示频率，对上述公式(6)进行整理得

根据定理1 和定理2 可知，公式(7)中的合并部分与MEM 的特征指数ψ(ω)相同，即

则公式(4)的PIDE 可化简为如下ODE

对公式(9)乘以积分因子eψ(x)t并进行求解得

其中C是常数.

因此，在任意0≤t1≤t2≤T时，计算出t2时刻的傅里叶变换后的期权定价，则可以计算出t1时刻的傅里叶变换后的期权价格

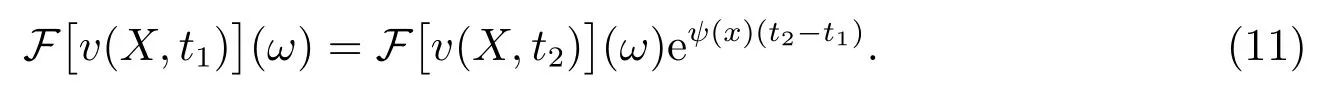
傅里叶逆变换如下

从而

连续傅里叶变换完成后，还需要在截断的风险资产价格域上实现傅里叶变换的离散化，即离散傅里叶变换(Discrete Fourier Transform, DFT).DFT 将对数资产价格从[-∞,∞]截断到区域Ω = [xmin,xmax].由奈奎斯特临界频率和时域的关系ωmax·ωmax-ωmin=N/2 可知，对于对数资产变量，需要选择一个适当的变化使得定价在x= 0 的邻域中.由此应该选择足够大的空间边界来捕获期权价值函数的整体行为，即让ωmax=-ωmin，使得函数区域位于中心，则傅里叶变换在Ω 上近似为

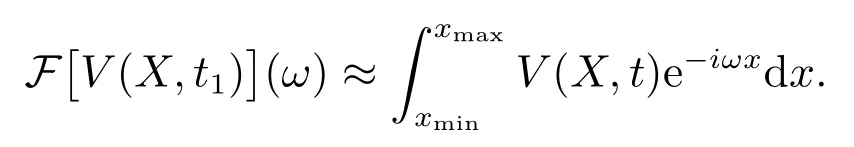
因为DFT 是在离散化的时域和频域下实现的，所以对于对数资产价格域的离散化，令xn=xmin+n·∆x,n=0,1,···,N-1 和另外，对于频域的离散化，令根据使用奈奎斯特频率条件，即得到因此期权价格v(X,t)在时间t上的离散傅里叶变换为

结合方程(14)和方程(11)，可以得到对数资产价格xn在时域中的价格，对于任何n=0,1,···,N-1 有

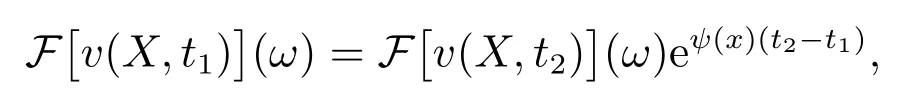
从而

其中v(X,t1)是时间t1在资产价格exn的期权价格.

4 数值模拟

本文利用Matlab 的DFT(x)和IDFT(x)函数实施FST 方法，讨论MEM 在m=2,n= 2 的情况下欧式看涨期权定价.假设MEM 的模型参数与文献[5]中的参数相同，即r= 0.05,θ1=η1,η2=θ2= 50,pu= 0.4,qd= 0.6,p1= 1.2,p2=-0.2,q1= 1.3,q2=-0.3,S0= 100,K= 100,t= 1.同时为了检验FST 方法的有效性，对于σ= 0.2 和σ= 0.3 的情况，分别给出不同η1下不同λ的数值计算，其中η1取值为20,40；λ的取值为1,3,5.为了进行数值方法的对比，我们也利用BA、FFT、MC 三种方法在上述参数下进行计算，并与FST 方法进行对比，其中FFT 方法的阻尼因子α= 1.21，MC 方法的模拟次数N= 100000，FST 方法截断区域Ω = [xmin,xmax]= [-7.5,7.5].本文所有实验都在Inter(R) Core(TM) i7-7700HQ CPU 2.80GHz，RAM为8.00GB 的计算机上进行.结果如表1 所示.

由表1 可知：四种方法中，MC 方法的运行时间最长，FFT 方法的运行时间最短，FST 方法次之.在计算精度上，以BA 方法为基准，FST 方法的计算结果与BA 最接近，相对误差最小为0.0002，最大为0.0004；FFT 方法的计算结果与BA 相差较大，相对误差最小为0.03，最大为0.2；与FST 方法相比，FFT 方法虽然CPU 运行时间上占据优势，但是精度低、不稳定.因此通过上述分析可知FST 方法具有精度高、稳定性好，运行时间短的优点.

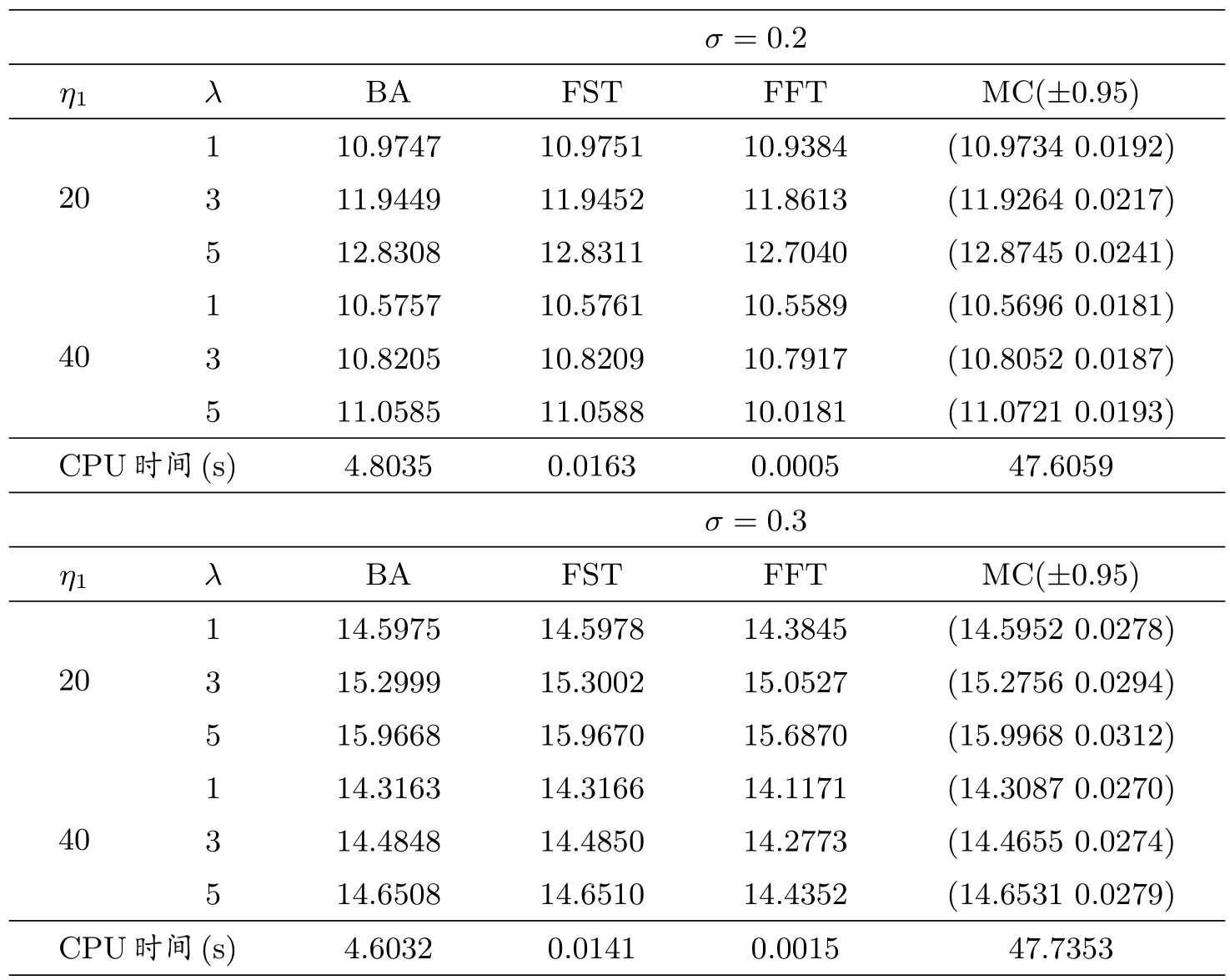
表1: 混合指数跳扩散模型(m=2, n=2)下BA、FST、FFT、MC 方法(括号里为MC 方法95%的置信区间)的欧式看涨期权定价结果对比

5 模型校正

5.1 非线性最小二乘法

期权定价是给定模型参数，再计算期权价格；而模型校正的思想是通过市场价格来反推理论模型的参数，使得通过模型得出的理论价格能够等于市场上交易的实际价格.所以模型校正和期权定价互为反问题.然而当模型是跳扩散模型时，通常无法保证反问题解的存在，因此我们采用非线性最小二乘法[20]解决该问题

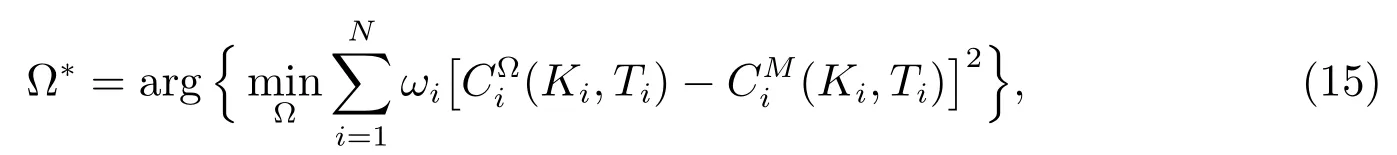
其中Ω 是模型参数，Ω∗是模型最优参数，分别是来自模型和市场的第i个期权价格，Ki和Ti分别是第i个期权的执行价格和到期时间，N是用于模型校正的期权数，ωi是加权因子.

设参数集Ω 的初始估计为Ω0，使用期权的中间价格作为市场价格

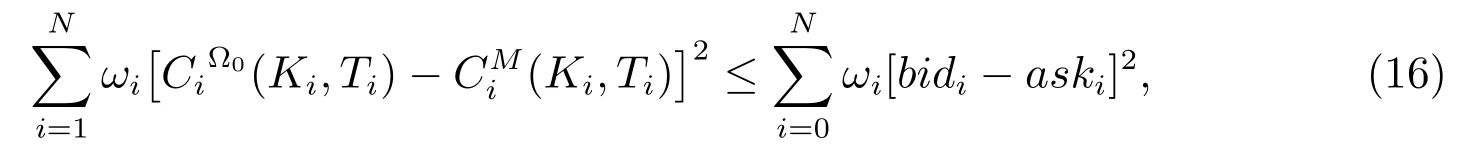
其中bid/ask为市场第i个期权的出价和开价.这意味着我们不要求模型准确复制市场价格，但平均来说，落在出价和开价区间内，这是校正过程的一个合理的放松，因为建模过程总是在一定的容许范围内产生的估计.

本文使用Matlab 中的lsqnonlin 函数实施校正算法[20].然而lsqnonlin 函数计算出的最优解和参数的初始值有关，因此得到的解可能不是全局最优，只能得到局部最优解.但只要(17)满足，利用lsqnonlin 函数求出的最优解就是可以接受的.

5.2 模型校正实证分析

我们仍然对MEM 在m=2,n=2 时进行模型校正，实证分析使用标准S&P 500[21]指数期权从2017.01 到2017.03 的数据，根据moneyness =K/S筛选出取值在0.94-1.06 之间的数据，并将满足(17)式的数据挑选出来.随后将这些数据分为三个部分，分别为取值在0.94-0.97 之间的价内期权(in-the-money, ITM)、0.97-1.03 之间的平价期权(at-the-money, ATM)和1.03-1.06 之间的价外期权(out-of-money, OTM).每个期权的出价和开价均已知，期权的到期时间从15 天到365 天不等，由于期权价格对利率不灵敏，且利率在每日的基础上变化很小，因而，设定无风险利率为年利率0.13.为了简便，假设市场无分红.

在模型校正中，以出价和开价的中间价格作为市场价格，根据5.1 可知，lsqnonlin 函数进行校正主要是对于初始参数x0的设置，可以通过不断的调整初始参数值进行重新校正.根据文献[5]，我们选择两组初始值进行参数设置，分别对ATM、ITM、OTM 进行校正，结果如表2 所示.

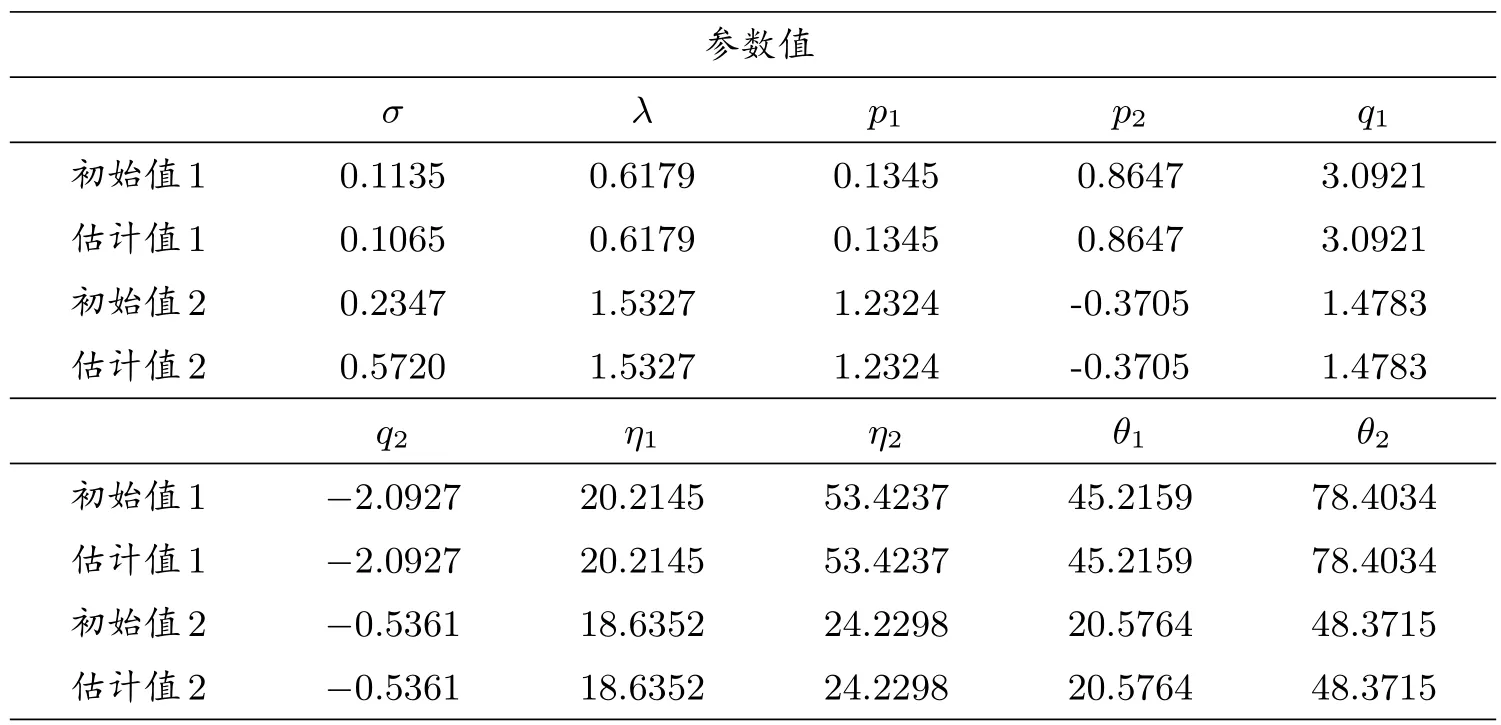
表2: 混合指数跳扩散模型(m=2, n=2)两组初始值的校正结果

为检验校正的效果，使用如下两个校正测度：平均相对百分比误差ARPE 和平均绝对百分比误差APE[22]

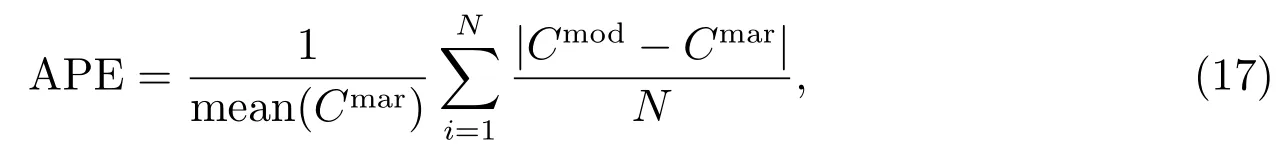
式中Cmod和Cmar分别表示期权基于模型的价格和市场价格，N是校正使用的期权个数，校正误差结果如表3 所示.

表3: 混合指数跳扩散模型(m=2, n=2)的校正误差

由上表可知，由于ITM,ATM 和OTM 这三个部分的数据校正后的参数估计值都相同，因此表2 分别给出两组初始值进行参数校正后的平均估计值.整体可以看出校正结果除第一个参数σ的结果出现细小的波动，其余参数的校正结果不变.而表3 的校正误差结果可以看出，基于两个初始值的误差非常小，不超过0.0006，由此表明了校正算法具有一定的稳定性.

根据表2 中的估计值2 绘制隐含波动率图，对于估计值2 中的10 个参数分别绘制隐含波动率图，其中参数λ和η1的隐含波动率图变化明显.因此，在其他参数不变的情况下，选取这两个参数进行隐含波动图的分析.其中，λ的取值分别为0.5375, 1.5375, 3.5375,5.5375；η1的取值分别为3.6352,8.6352,18.6352,28.6352.绘制三维曲线图，其中执行价格为0.8-1.2，距离到期日的时间间隔为0.04-1 年，结果如图1 和图2 所示.

根据上图可知，由于资产收益分布的非对称性，可以看出图1 和图2 的隐含波动率曲线不是对称的，且体现出明显的“波动率微笑”特征.图1 为不同λ下资产收益的隐含波动率图.可以看出随着λ的增大，期权的隐含波动率相对变大，表明参数λ的变化对于隐含波动率的影响显著；图2 为不同η1下资产收益的隐含波动率图.可以看出随着η1的增大，隐含波动率图像变化明显，在η1= 18.6352 时，图像趋于稳定，表明η1取值相对较小时，对于隐含波动率的影响较大.

6 结论

本文使用傅里叶空间时间步长法(FST)求解混合指数跳扩散模型(MEM)下欧式期权定价过程中产生的PIDE 问题.利用FST 方法，我们在MEM 模型下获得了欧式期权的数值解，并对结果进行对比分析，相对于蒙特卡洛模拟(MC)、快速傅里叶变换(FFT)、以及欧拉反演(BA)，FST 方法更加有效.然后进行模型校正，结合最小二乘法和S&P 500 指数期权数据进行实证分析，得到模型的参数值，并绘制了MEM 的隐含波动率图像，结果表明MEM 很好地体现资产收益的“波动微笑”等特征，而且参数λ和η1对隐含波动率有重要影响.

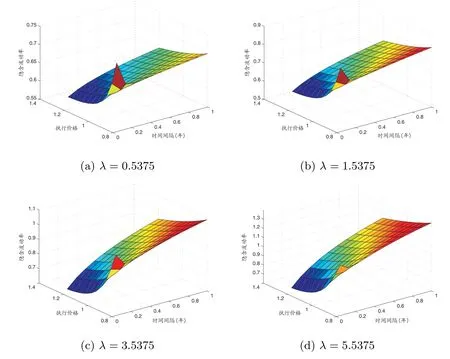
图1: 混合指数跳扩散模型(m=2, n=2)在不同λ 下的隐含波动率图

图2: 混合指数跳扩散模型(m=2, n=2)在不同θ1 下的隐含波动率图