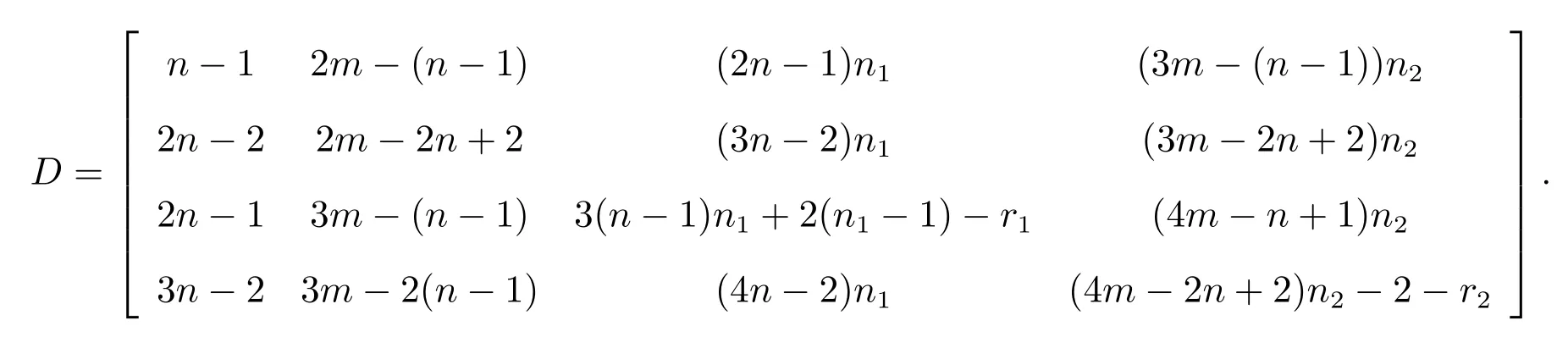Depiction Technology of Super Corona Distance Matrix Spectrum

XU Xiao-jing, WANG Pei-wen, WANG Zhi-ping

(1- College of Science, Dalian Maritime University, Dalian 116026;2- College of Shipping Economics and Management, Dalian Maritime University, Dalian 116026)

Abstract: The topological structure of the graph has important significance in chemical molecular structure, and the various matrices of the graph contain the topology information of the graph.In this paper, we depict the distance spectrum of four kinds of double corona, according to the definition of distance spectrum and the structure characteristics of four types of graphs, the corresponding distance matrix is obtained by mathematical induction.On the basic of them, the block matrix is constructed, which is a super corona distance matrix.By using the uniqueness of the matrix eigenvalues, the eigenvalues and eigenvectors of the super corona distance matrix are solved, and the accuracy and reliability of the conclusion are verified simultan-eously.Finally, we research the distance spectrum of G(S)◦{G1,G2},G(Q)◦{G1,G2}, G(R)◦{G1,G2}, G(T)◦{G1,G2}, when G is a complete graph and G1, G2 is a regular graph.

Keywords: corona; distance spectrum; double corona; super corona distance matrix

1 Introduction

Throughout in this article we consider only simple graphs.LetG= (V,E) be a graph with vertex setV={v1,v2,···,vn} and edge setE={e1,e2,···,em}.LetM(G) be the vertex-edge incidence matrix ofGandA(G) be the adjacency matrix ofG.The distance matrixD(G)=[dij]of a graphGis the matrix indexed by the vertices{v1,v2,···,vn} ofG, wheredij=d(vi,vj) is the distance between the verticesviandvj,i.e.,the length of a shortest path betweenviandvj.SinceD(G)is a real symmetric matrix,its eigenvalues called distance eigenvalues ofGwhich are all real.The spectrum ofD(G) is denoted by specD(G) ={ρ,θ2,···,θn} and is called the distance spectrum of the graphG.The spectrum ofA(G) is denoted by specA(G)={λ1,λ2,···,λn} and is called the adjacency spectrum of the graphG.

Following notations are being used in the rest of the paper.The Kronecker product of matricesA=[aij]andBis defined to be the partitioned matrix[aijB]and is denoted byA ⊗B.Them×1 vector withi-th entry equal to one and all other entries equal to zero is denoted byϵi.Then× 1 vector with each entry 1 is denoted by 1n.ByJn, we denote the matrix of all ones of ordern.ByIn, we denote the identity matrix of ordern.Kndenotes the complete graph of ordern.The distance characteristic polynomial ofGis that ofD(G), that is, the polynomialPD(λ) definedPD(λ)=det(λI-D(G)).

LetGbe a connected graph onnvertices andmedges,andHbe any graph.Then it is well known that the coronaG ◦HofGandHis the graph obtained by taking one copy ofGandncopies ofHand then by joining thei-th vertex ofGto every vertex in thei-th copy ofH.Bariket al[1]have characterized both adjacency and Laplacian spectrum of corona of two graphs.The edge corona of two graphs is defined similarly,see [2]for definition and its spectral characterization.The neighbourhood corona ofGandHhas been defined by Gopalapillai[3], which is based on the idea that thei-th neighbouring vertices ofGare connected to every vertex in thei-th copy ofH.In[4,5],the graphs such asR-vertex corona,R-edge corona,R-vertex neighbourhood corona,R-edge neighbourhood corona,subdivision-vertex neighbourhood corona and subdivisionedge neighbourhood corona graphs are considered and the coronal technique is used to find the spectrum of these graphs.Recently, Indulal and Stevanovi[6]described the distance spectrum of coronaG ◦Hand clusterG{H} of two graphs, whereGis connected distance regular andHis regular.In[7,8],the author described the distance spectrum of complements of trees and threshold graphs.

This work is motivated by[9]in which Sasmita Barik and Gopinath Sahoo described the distance spectra of coronasG◦H,whenGis connected transmission regular andHis regular and also from a recent work[10]in which the authors describe the Laplacian spectrum of corona of some variants of corona.Motivated by all these we depict the distance eigenvalues and eigenvectors of several double corona.

Definition 1[10]LetGbe a connected graph onnvertices andmedges.LetG1andG2be graphs onn1andn2vertices, respectively.The subdivision double corona ofG,G1andG2, denoted byG(S)◦{G1,G2}, is the graph obtained by taking one copy ofS(G),ncopies ofG1andmcopies ofG2and then by joining thei-th old-vertex ofS(G) to every vertex of thei-th copy ofG1and thej-th new-vertex ofS(G) to every vertex of thej-th copy ofG2.In place ofS(G), if we takeQ(G)(R(G),T(G)), then the resulting graph is called asQ-graph (R-graph, total) double corona and denoted by

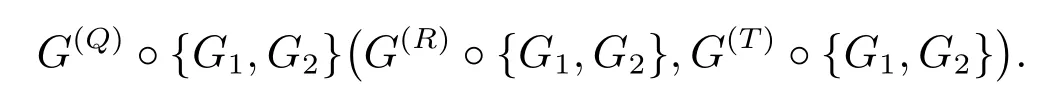
Note that all the above four graphs containn(n1+1)+m(n2+1)number of vertices.

Example 1[10]Consider the graphsG=C4,G1=P3andG2=P2, wherePndenotes the path of ordern.Figure 1 describes the four graphs

Figure 1: Subdivision (Q-graph, R-graph，total) double corona

In section 2, looking at the similarities in the proofs of the results describing the distance spectra of several double corona graphs,we define a block matrix forms named as super corona matrix and depict their spectra.Using the spectra of the matrix we obtain the distance eigenvalues and eigenvectors of several double corona in successive sections.

2 Super corona distance matrix

LetGbe a complete graph onnvertices andmedges.LetG1be ar1-regular graph onn1vertices with an adjacency matrixA(G1) andG2be ar2-regular graph onn2vertices with an adjacency matrixA(G2).

Taking the subdivision double corona graph as example to introduce the establishment of distance matrix.The distance matrix ofis

By observing the rules of each part of the above special distance matrix and structures of the subdivision double corona graph, we conclude that the distance matrix ofG(S)◦{G1,G2} is

Similarly,the distance matrix ofG(Q)◦{G1,G2},G(R)◦{G1,G2}andG(T)◦{G1,G2}are as follows.

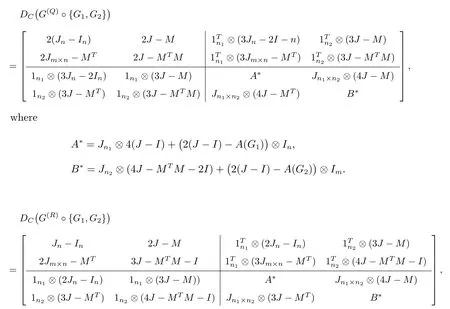
Because the distance matrix is symmetric, we just have to determine the diagonal and the block matrix in the upper right corona.Summarizing the common features according to the characteristics and structures of four double corona distance matrices,we build the super corona distance matrix.

Letn,m ∈N,n ≤m,n1,n2∈N∪{0},where N is the set of positive integers.LetA,C,D,Ebe real square matrices of ordern,m,n1,n2andBbe an×mreal matrix.Considering the following one real square matrices of ordern(n1+1)+m(n2+1):

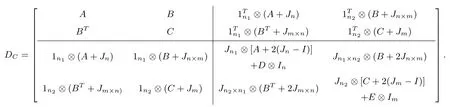
We callDCas the super corona distance matrix, respectively, if they satisfy the following conditions:

(i) IfXiandYiare the singular vector pairs corresponding to singular valuesbiofBfori= 1,2,···,n, whereX1= 1n,Y1= 1m, thenXiandYiare orthogonal eigenvectors ofAandC, respectively.That is, ifBYi=biXiandBTXi=biYifori=1,2,···,n, thenAXi=aiXiandCYi=ciYiwhereaiandciare the eigenvalues ofAandC, respectively;

(ii) IfB= 0nforj= 1,2,···,m-n(this is true asn ≤m), thenis orthogonal eigenvectors ofC, that isforj= 1,2,···,m-n, whereis eigenvalues ofC;

(iii) 1n1is an eigenvector ofD;

(iv) 1n2is an eigenvector ofE.

Letd1(=dsay),d2,···,dn1be the eigenvalues ofDwith the corresponding eigenvectors as 1n1=Z1,Z2,···,Zn1, respectively.Similarly, lete1(=esay),e2,···,en2be the eigenvalues ofEwith the corresponding eigenvectors as 1n2=W1,W2,···,Wn2,respectively.

The following result depicts all the eigenvalues and the corresponding eigenvectors of the super corona distance matrix.

Theorem 1LetDCbe a super corona distance matrix of ordern(n1+1)+m(n2+1) as defined above.Then the spectrum ofDCconsists of:

(i) All the roots of the following equation

(iii)djrepeatedntimes, forj=2,3,···,n1;

(iv)ejrepeatedmtimes, forj=2,3,···,n2;

(v) All the roots of the following equation det(λI-D)=0, where

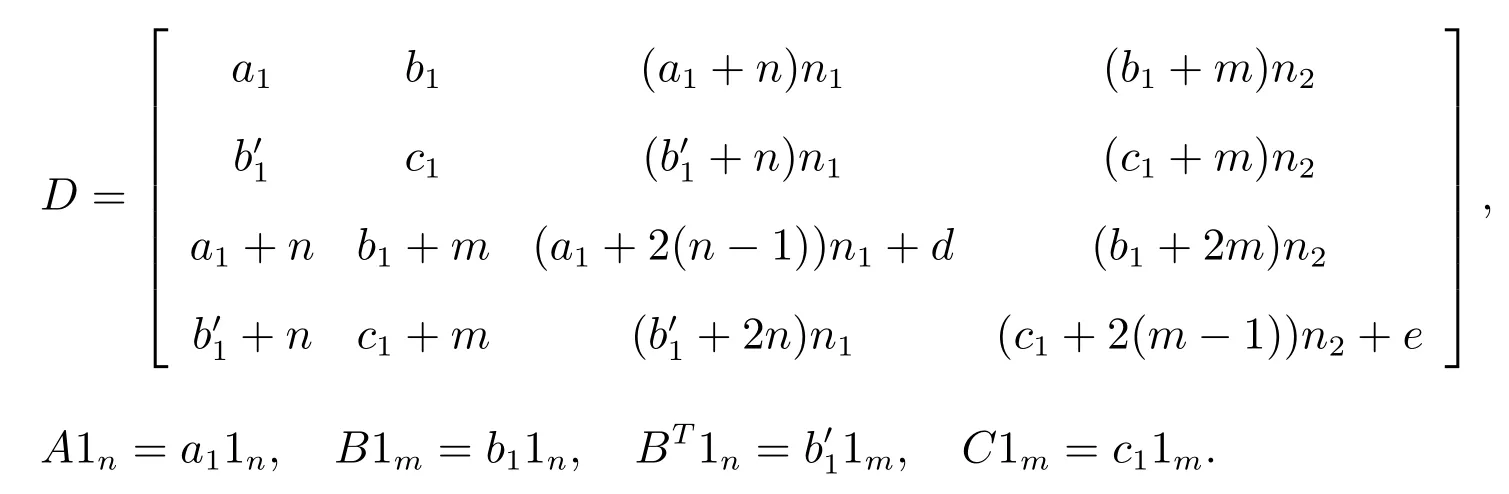
Proof(a) To prove (i), we suppose that the vector

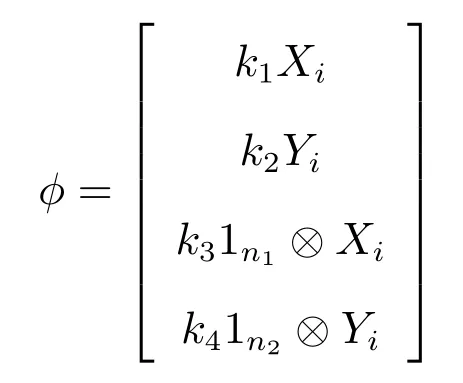
is an eigenvector ofDCcorresponding to the eigenvalueλ.

Consider the matrix equation

wherek1,k2,k3,k4andλare the unknown constants to be determined.

BecauseBYi=biXi,BTXi=biYi,AXi=aiXi,CYi=ciYi,D1n1=d1n1,E1n2=e1n2,i=1,2,···,nandXi ⊥1n,Yi ⊥1m,i=2,3,···,n.

The first row element on the left hand of the (1) is

The second row element on the left hand of the (1) is

The third row element on the left hand of the (1) is

The fourth row element on the left hand of the (1) is

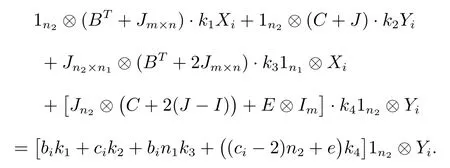
Comparing both sides of (1), we get

Note thatλ=d-2n1orλ=e-2n2is not satisfied with the above equation.

Supposingk1=1 and solving (2)-(5), we get

With (2)×ci-(3)×bi, we get

whereλ0.

We substitute the value ofki(i= 1,2,3,4) into (2).Then we get characteristic polynomial of the super corona distance matrixDC,

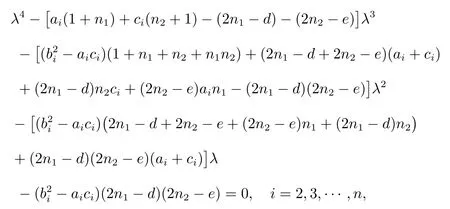
whenλ= 0, from equations, we getin other words

Hence the proof of (i) follows.

(b) Asn ≤m, there existsm-northogonal vectorsforj= 1,2,···,m-nsuch thatB=0nfor which we haveforj=1,2,···,m-n.

To prove (ii), we suppose that the vector

is an eigenvector ofDCcorresponding to the eigenvalueλ.

Consider the matrix equation

wherek1,k2andλare the unknown constants to be determined.Comparing both sides, we get

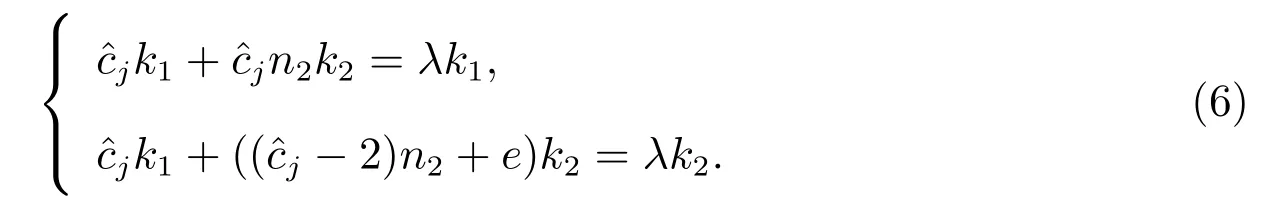
Eliminatingk1andk2from these equations, we get

Hence the proof of (ii) follows.

(c) To prove (iii), observe that

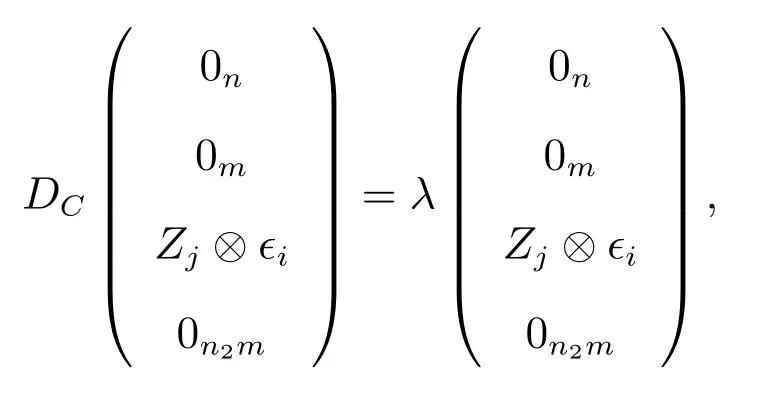
forj= 2,3,···,n1andi= 1,2,···,n, whereϵiis a vector of lengthnwhose all components are zero except thei-th component which is 1.we getλ=dj.

(d) Similarly it can be observed that

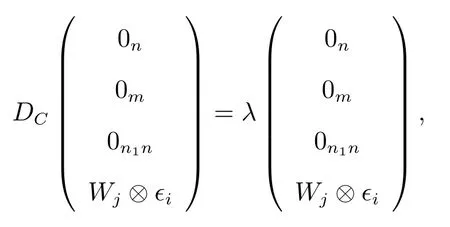
forj= 2,3,···,n2andi= 1,2,···,n, whereϵiis a vector of lengthnwhose all components are zero except thei-th component which is 1.we getλ=ej.

(e) To prove (iv), we suppose that the vector

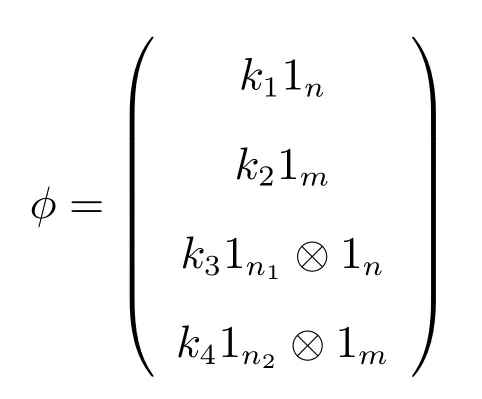
is an eigenvector ofDCcorresponding to the eigenvalueλ.

Suppose thatA1n=a11n,B1m=b11n,

Consider the matrix equation

wherek1,k2,k3,k4andλare the unknown constants to be determined.(6) does the same to (1) in solving process.Comparing both sides, we get

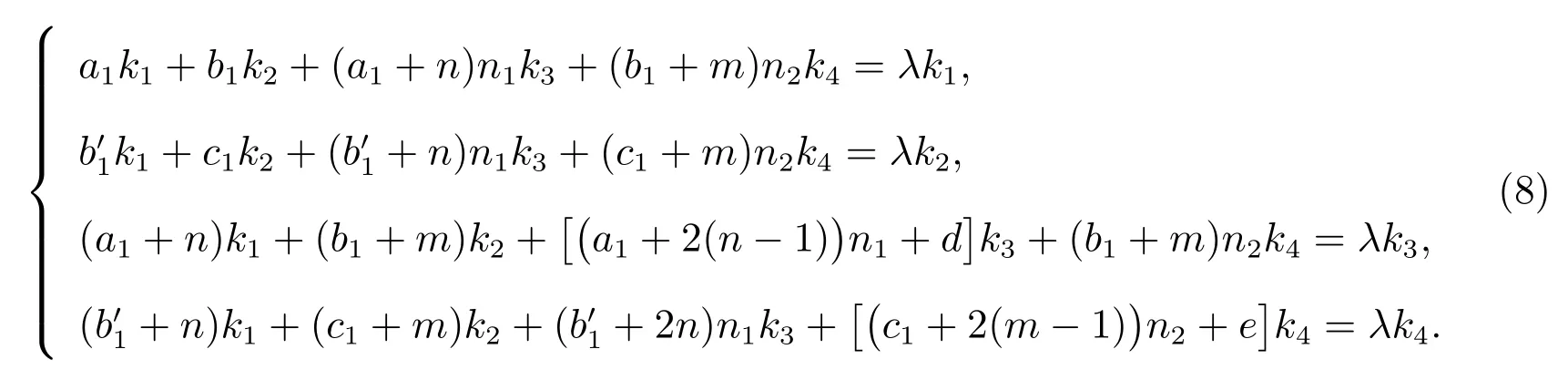
Ask1,k2,k3,k4are not all 0 by Kramer’s Theory, the determinant of coefficient of the homogeneous linear equations satisfy det(λI-D)=0.Where

This prove (v).

Thus we have listed all then(n1+1)+m(n2+1)eigenvalues ofDCwhich completes the proof.

Example 2Consider the subdivision double corona graphThen the distance matrix of

Solution 1Through a Matlab program,the distance spectrum ofis

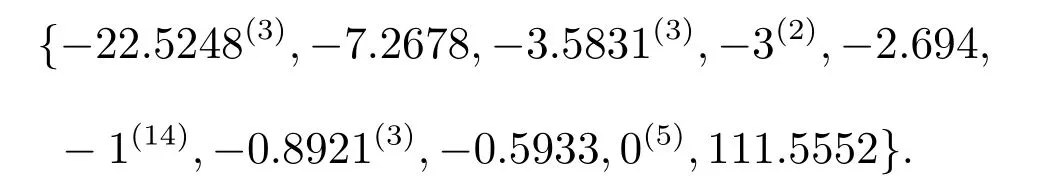
The program of Matlab see attachment.

Solution 2By using Theorem 1, we have

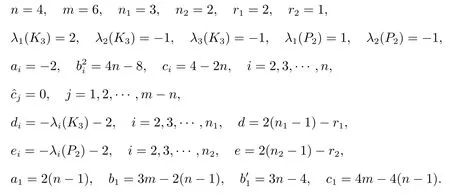
Now substituting these values in Theorem 1.

(i) All the roots of equationλ4+27λ3+104λ2+72λ= 0, fori= 2,3,4.With Matlab, the roots of the equation are 0,-22.5248,-3.5831,-0.8921(i=2,3,4);

(ii) 0 and 3,j=1,2;

(iii)-1 repeated 4 times,i=2,3;

(iv)-1 repeated 6 times,i=2;

(v) The roots of the following equation det(λI-D) = 0 are 111.5552,-7.2678,-0.5933,-2.6940, where

We solved the distance spectrum ofby two different methods and the result is the same.Then Theorem 1 is accurate.

3 The application of supper corona distance matrix spectrum

In this section, we depict the distance spectra of the four double corona graphs which defined earlier by using Theorem 1.The following results depicts all the distance eigenvalues of subdivision double corona graphs.

Proposition 1LetGbe a complete graph onnvertices andmedges.LetG1be ar1-regular graph onn1vertices with an adjacency matrixA(G1) and specA(G1)={r1=λ1(G1),λ2(G1),···,λn1(G1)}.LetG2be ar2-regular graph onn2vertices with an adjacency matrixA(G2) and specA(G2) ={r2=λ1(G2),λ2(G2),···,λn2(G2)}.Then the distance spectrum ofG(S)◦{G1,G2} consists of:

(i) All the roots of the equation

(ii) 0 and-r2-2, forj=1,2,···,m-n;

(iii)-λi(G1)-2 repeatedntimes, fori=2,3,···,n1;

(iv)-λi(G2)-2 repeatedmtimes, fori=2,3,···,n2;

(v) All the roots of the following equation det(λI-D)=0, where

ProofBy a harmonious labeling of vertex set, the distance matrix ofG(S)◦{G1,G2} can be expressed in the form

where

whereMis incidence matrix ofG.

Now, comparing with the super corona distance matrixDC, we have

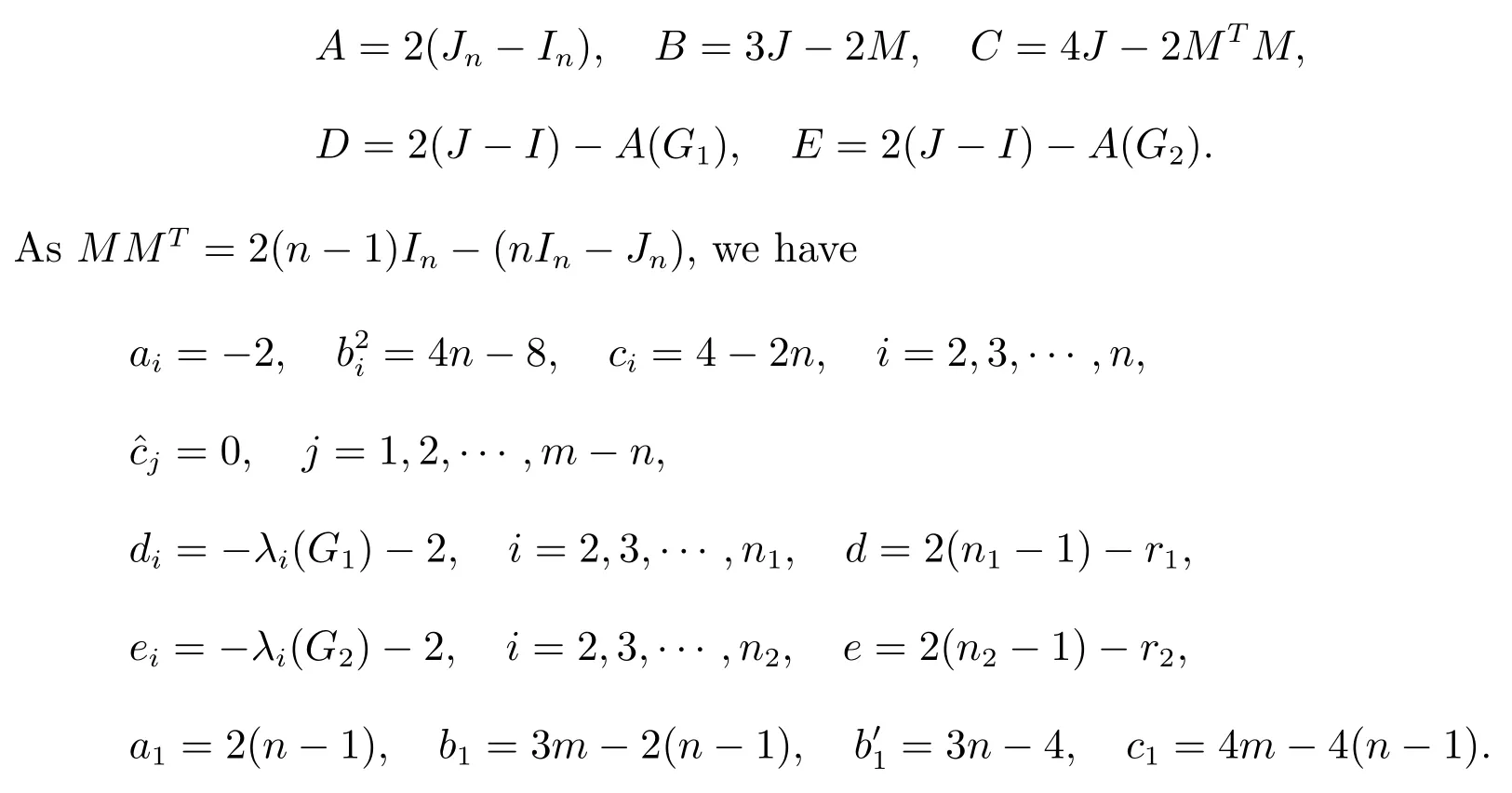
Now substituting these values in Theorem 1, the result is following.

Because the proof is similar, we just give the following result of theQ(R,T)-graph double corona.

Proposition 2LetGbe a complete graph onnvertices andmedges.LetG1be ar1-regular graph onn1vertices with an adjacency matrixA(G1) and specA(G1)={r1=λ1(G1),λ2(G1),···,λn1(G1)}.LetG2be ar2-regular graph onn2vertices with an adjacency matrixA(G2) and specA(G2) ={r2=λ1(G2),λ2(G2),···,λn2(G2)}.Then the distance spectrum ofG(Q)◦{G1,G2} consists of:

(i) All the roots of the equation

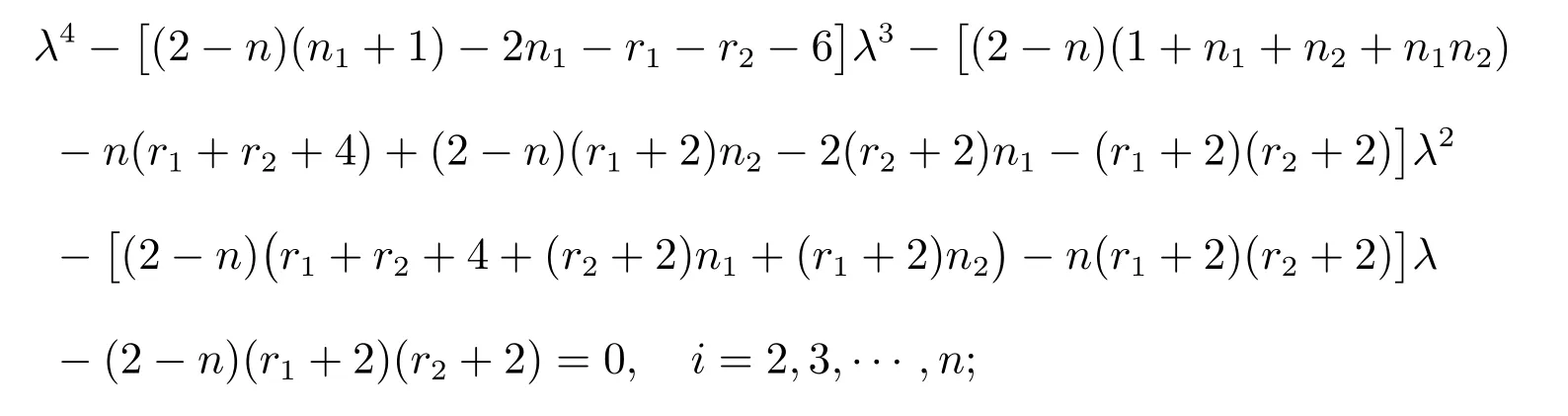
(ii) 0 and-r2-2, forj=1,2,···,m-n;

(iii)-λi(G1)-2 repeatedntimes, fori=2,3,···,n1;

(iv)-λi(G2)-2 repeatedmtimes, fori=2,3,···,n2;

(v) All the roots of the following equation det(λI-D)=0, where

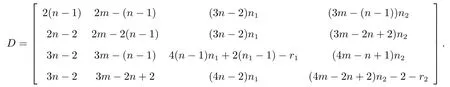
Proposition 3LetGbe a complete graph onnvertices andmedges.LetG1be ar1-regular graph onn1vertices with an adjacency matrixA(G1) and specA(G1)={r1=λ1(G1),λ2(G1),···,λn1(G1)}.LetG2be ar2-regular graph onn2vertices with an adjacency matrixA(G2) and specA(G2) ={r2=λ1(G2),λ2(G2),···,λn2(G2)}.Then the distance spectrum ofG(R)◦{G1,G2} consists of:

(i) All the roots of the equation

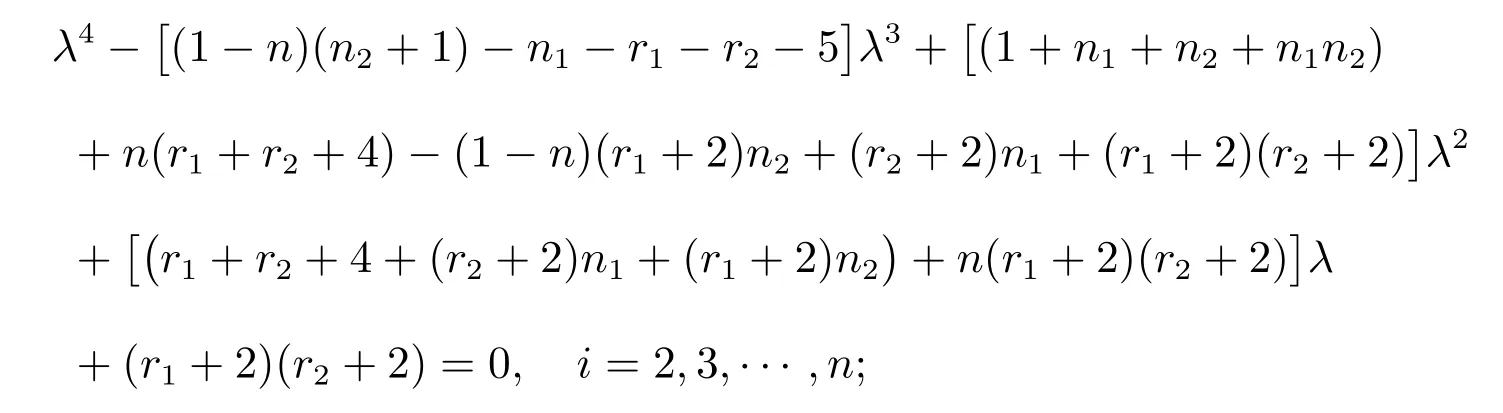
(ii)

(iii)-λi(G1)-2 repeatedntimes, fori=2,3,···,n1;

(iv)-λi(G2)-2 repeatedmtimes, fori=2,3,···,n2;

(v) All the roots of the following equation det(λI-D)=0, where

Proposition 4LetGbe a complete graph onnvertices andmedges.LetG1be ar1-regular graph onn1vertices with an adjacency matrixA(G1) and specA(G1)={r1=λ1(G1),λ2(G1),···,λn1(G1)}.LetG2be ar2-regular graph onn2vertices with an adjacency matrixA(G2) and specA(G2) ={r2=λ1(G2),λ2(G2),···,λn2(G2)}.Then the distance spectrum ofG(T)◦{G1,G2} consists of:

(i) All the roots of the equation

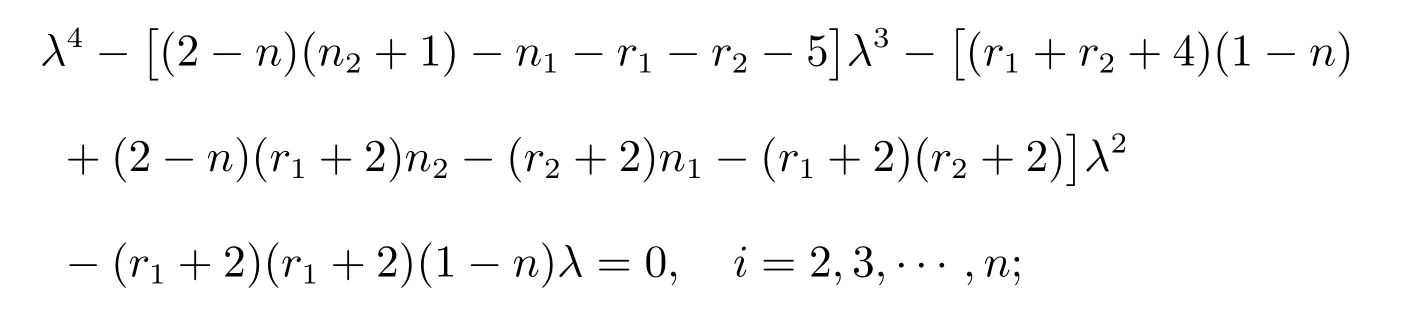
(ii) 0 and-r2-2, forj=1,2,···,m-n;

(iii)-λi(G1)-2 repeatedntimes, fori=2,3,···,n1;

(iv)-λi(G2)-2 repeatedmtimes, fori=2,3,···,n2;

(v) All the roots of the following equation det(λI-D)=0, where