Logistic组稀疏回归模型的Bayes建模及变分推断

沈圆圆, 曹文飞, 韩国栋

(陕西师范大学数学与信息科学学院，西安 710119)

1 引言

Logistic 回归是统计分析中基本且十分重要的预测模型，在风险预测、流行病学及生物分析等领域具有广泛应用[1-3].在Logistic 回归中，模型的变量选择与参数估计是解决统计问题的关键.考虑一般的Logistic 回归模型

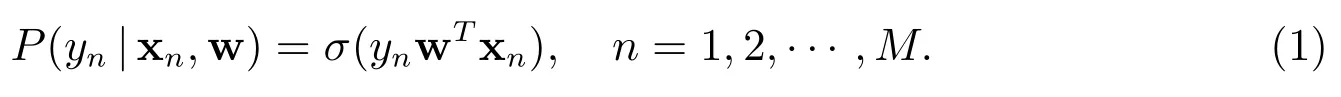
这里

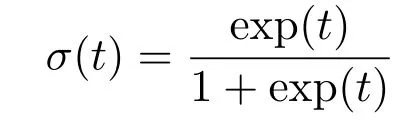
表示 sigmoid 函数，w∈RN表示回归系数向量，xn= (xn1,xn2,···,xnN)T是第n个输入向量，yn={-1,1}是对应的二元响应变量，M表示观测样本的数目.所有的输入向量放到一起构成M×N设计矩阵所有的响应变量放到一起构成响应向量 y=(y1,y2,···,yM)T.

Logistic 回归的一般目标是基于一组观测样本(xn,yn),n=1,2,···,M，设计某种准则估计回归系数w.最大似然准则是参数估计中经典准则之一.Logistic 回归模型(1)经过最大似然准则得到如下估计

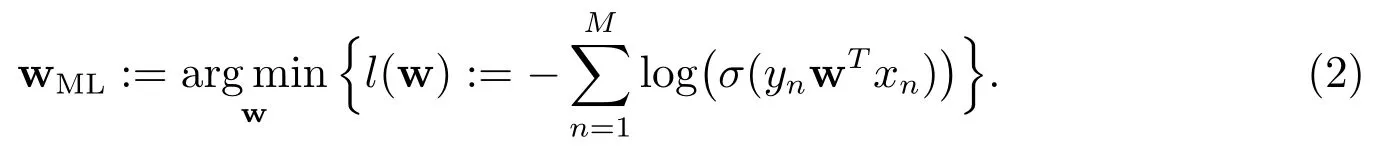
在实际问题中，该似然估计一般是可行的，但对于高维问题，该估计往往会失效，而且该估计不具有变量选择的功能.在应对高维问题并嵌入变量选择功能方面，Lasso[4]是一个十分成功的准则.Logistic 回归模型(1)经过Lasso 准则得到如下估计

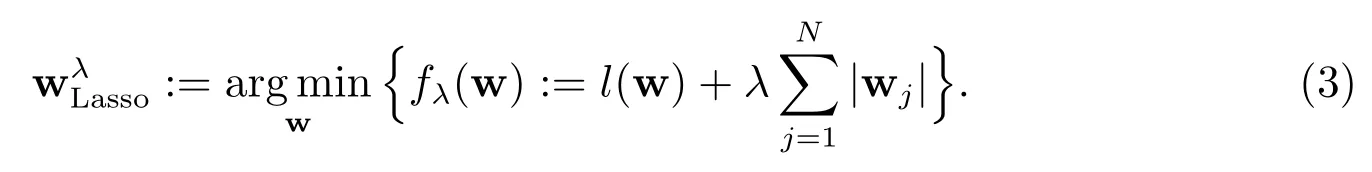
上述Logistic Lasso 估计通过施加ℓ1惩罚诱导出稀疏性，从而实现了变量选择.与最佳子集选择、逐步回归等方法相比，Lasso 估计有巨大的计算优势.但是，Lasso 做变量选择时仅依赖于单个输入变量而没有注意到各个变量之间的关系，因此常常会选择出一些不太重要的变量.此外，Lasso 解依赖于因子间的正交方式，即对一个分类预测子选择不同的正交方式将产生不同的解，这是不合理的，因为因子选择和估计问题的解不应取决于因子是怎样编码的.

Group Lasso[5,6]适当扩展了Lasso 惩罚，在一定程度上克服了上述问题.Kim 等人[7]首次将Group Lasso 应用于Logistic 回归模型(1)，并设计出了一个有效的推断算法.在此基础上，Meier 等人[8]提出来一个改进的方法，得到了Logistic Group Lasso 估计

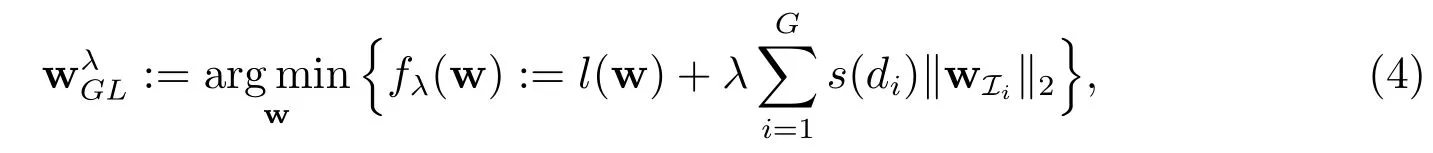
其中Ii是属于第i个变量组的指标集，i=1,2,···,G，G是组的数目，为第i组的数目.显然，(4)中的惩罚项可视为介于ℓ1和ℓ2之间的惩罚，并且包含ℓ1范数作为特殊情形.注意到在(4)中，由于稀疏性被施加在组上而不是单个变量上，因而该估计考虑到了信号元素之间的相互关系，并且该估计在群组正交重新参数化下不变，从而一定程度上克服了Lasso 的缺点.Logistic Group Lasso 估计(4)在高维统计、压缩感知[9,10]、机器学习[6,11]以及图像与网络分析[12-14]等领域均显示出良好性能.

但是，计算Logistic Group Lasso 估计(4)时需要通过交叉验证方法确定模型参数λ的最优值，该过程无论在数据量还是计算上都需要很大的代价.而且基于该准则的点估计导致对新样本x0的预测是一个硬的二元决策，而在理想情况下，我们期望在该新样本上的预测是一个条件分布，并通过此条件分布来捕获预测中的不确定性.

为了克服上述优化方法的弊病，本文提出一个新的Bayes 概率方法来解决Logistic 组稀疏建模与推断问题.具体来说，首先使用高斯-方差混合公式建模组稀疏参数向量先验的分层结构；其次，基于变分Bayes 方法导出所有参数的后验推断公式；最后，基于参数的后验公式导出新样本的概率预测公式.值得指出的是，用高斯-方差混合公式可以带来诸多优点，如参数向量的高斯分布建模使得积分计算容易实现、共轭先验机制可以给出参数的闭式估计、以及参数的自动化估计将省略掉调制超参数的复杂过程等.

本文内容组织如下：第2 节，建立Logistic 组稀疏回归的概率模型；在第3 节，基于变分Bayes 方法，推导模型中相关参数的后验推断公式，并给出有效算法框架；基于回归参数的后验概率公式，在第4 节中导出新样本的预测密度；第5 节中的多组模拟数值实验将验证所提出方法具有良好的分类性能；最后一节总结本文工作并展望后续的研究问题.

2 Logistic组稀疏回归的Bayes建模

本节我们将提出Logistic 组稀疏回归模型的Bayes 概率版本.首先，给出数据似然的分布形式；其次，利用高斯-方差混合分布给出回归参数w 组稀疏的概率刻画；最后，构建出所有分布参数的超先验分布，从而为整个生成过程建立一个全Bayes 概率模型.

下文中diag(v)为对角阵，v 为对角线元素组成的向量，〈·〉是关于相应分布的期望.

2.1 数据似然

数据yn=1 或yn=-1 依赖于N维输入xn.假设对数似然比

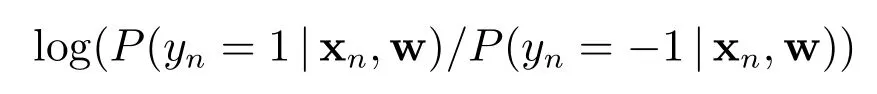
关于xn是线性的，yn=1 的条件似然由sigmoid 函数给出，即

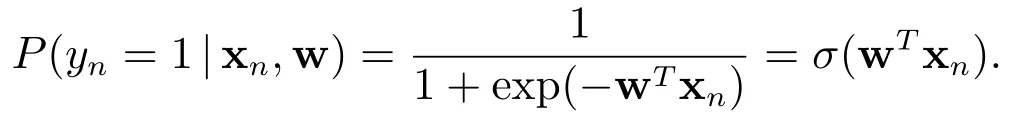
易见

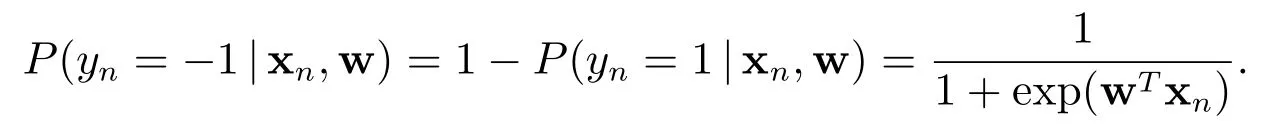
此时，条件分布密度函数可建模为

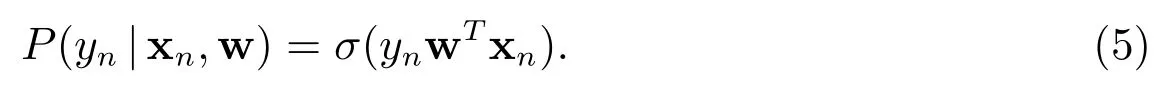
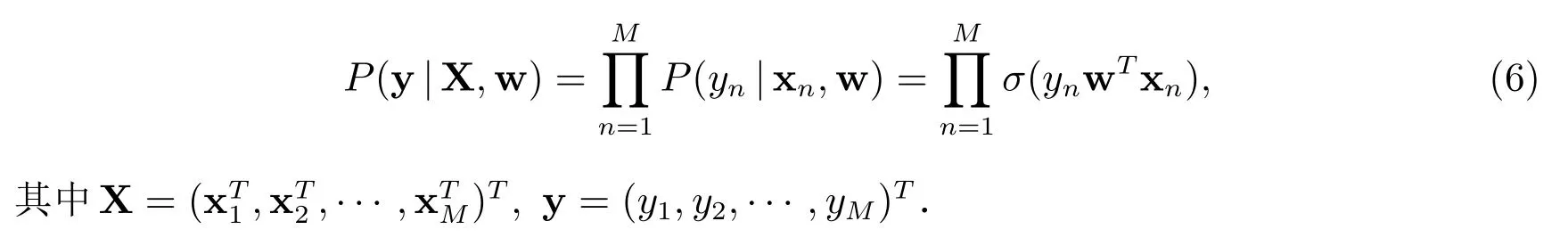
2.2 参数w建模

假定参数 w 可划分为G组，wi表示第i组 (i=1,2,···,G)，该组有di个参数.特别地，当G=N时，每组都只有1 个参数，即退化为不分组情形.

各组之间的先验一般假设是独立的，这种假设在很多实际问题中经常被采用，例如多频带信号重建[15]、微阵列分析[16]等.在此假设下，回归参数w 条件分布的乘积形式为

于是，回归参数w 的整体概率建模问题转化为各分组回归参数wi的概率建模问题.我们将采用高斯-方差混合公式[17]的分层概率建模机制来实现回归参数w 的组稀疏性质.

对zi积分，可得wi的边缘分布

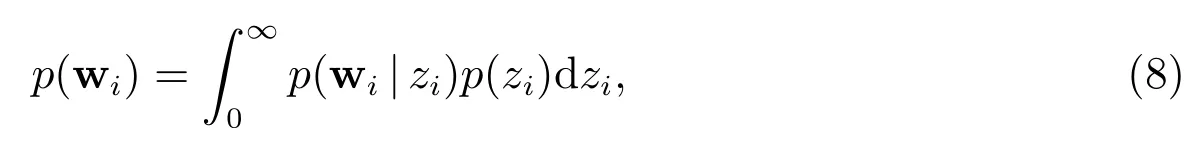
其中p(zi)称为混合分布.选择一个恰当的混合分布可以保证(8)式中积分能给出显式解，从而有利于后续参数推断.因此，混合分布的选择对参数推断是至关重要的.

本文中，我们选取伽马分布

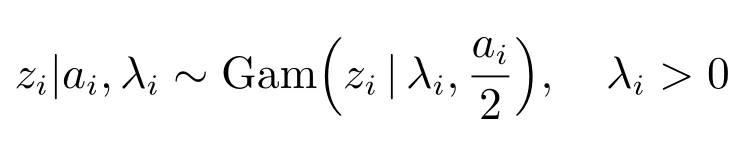
作为混合分布p(zi)的具体形式，其密度函数为

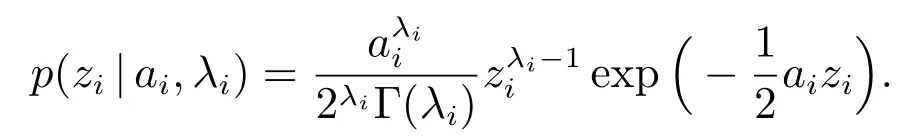
将此混合分布代入等式(8)，可以得到关于回归参数wi的边缘分布

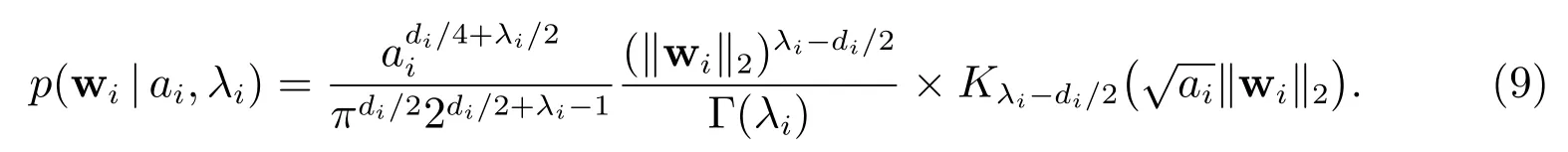
该边缘分布被称作Mckay’s Bessel 函数分布[18]，其中Kλi是二阶修正Bessel 函数.

至此，我们得到了wi的边缘分布(9).该分布具有尖峰厚尾形式，因而可以诱导出稀疏解.从(9)式中可以看到，该分布具有超参数ai与λ.为避免繁琐的超参数调制，接下来将在第3 节给出ai的先验建模，本文中对参数λ我们不对它有封闭形式的更新，只需要它有数值解，把它看作一个自由参数，具体值将在第3 节说明.

3 变分推断

在本节中，我们将利用变分Bayes 方法[19,20]，给出后验概率p(w,z,a|y)的近似推断.为方便叙述，记为ϵ:={w,z,a}，近似后验概率分布记为q(ϵ).q(ϵ)与p(ϵ|y)之间的Kullback-Leibler 散度(以下简称KL 散度)为

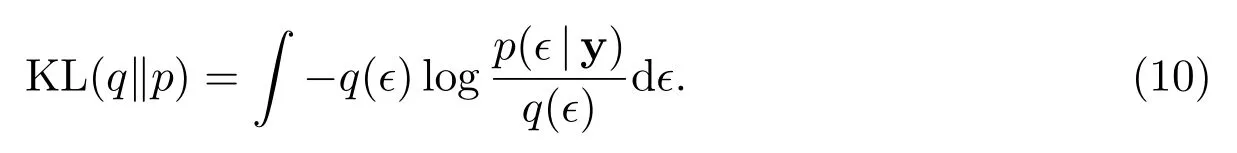
以下，我们将通过最小化KL 散度来求得q(ϵ).

将p(ϵ,y)=p(ϵ|y)P(y)及联合分布

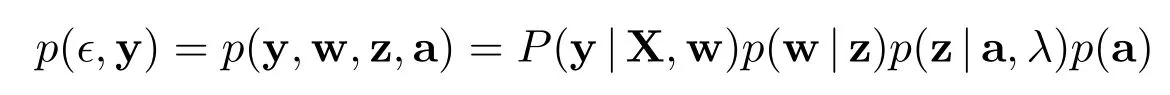
代入上式，可以得到

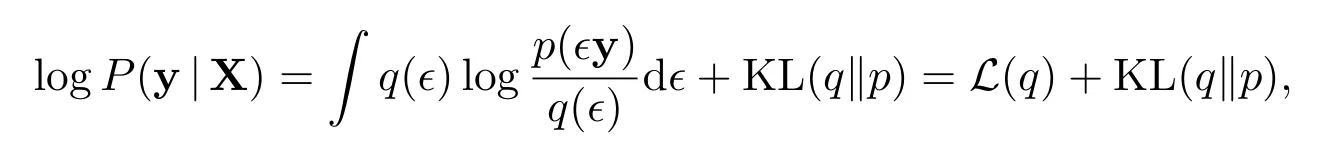
其中L(q)称为变分下界.对于固定的观测y，易知上式左边为常数.因此，KL 散度最小等价于变分下界L(q)最大.进一步，假设后验参数变量相互独立，可得q(w,z,a) =q(w)q(z)q(a).此时，变分下界为

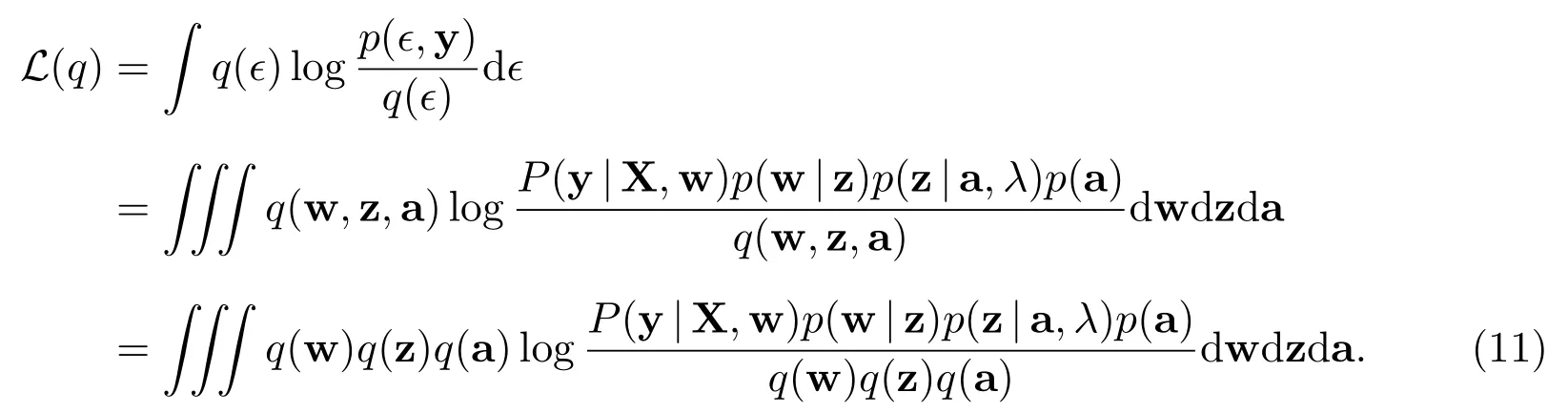
由于数据似然(6)在指数族上不存在共轭先验，导致上式中变分下界L(q)关于后验概率分布q(w)、q(z)及q(a)的极大值点没有显式解.因此，需要对数据似然做进一步的处理.

考虑sigmoid 函数的一个下界函数

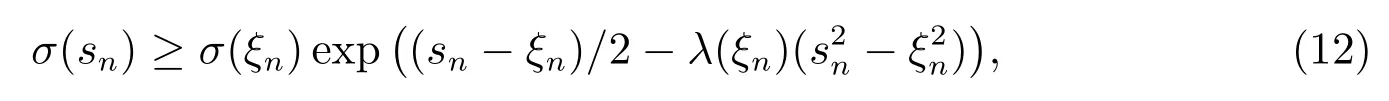
值得注意的是，每个数据均有一个局部的变化参数ξn.用h(w,ξ)代替数据似然P(y|X,w)，代入(11)，可得新的变分下界

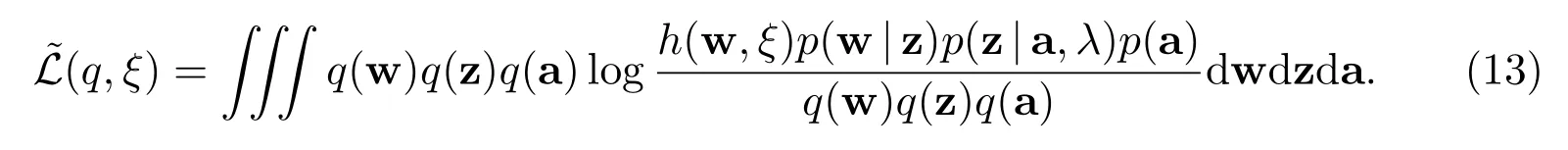
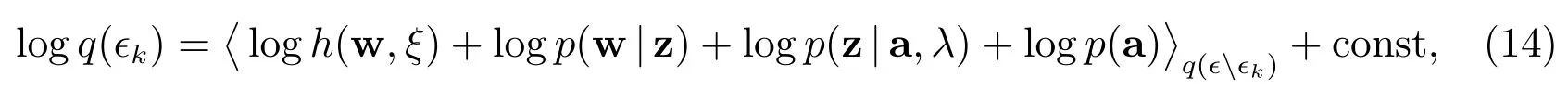
其中ϵϵk表示在ϵ中移除掉ϵk.注意到，上式左边参数的后验分布是通过右边参数的分布表达出来，而右边参数的分布又是未知的，因此需要通过一个迭代过程才能给出最终解.以下，我们将根据(14)式，计算出当ϵk分别等于w、z 及a 时的具体分布；最后，通过迭代给出详细的算法框架.

3.1 估计参数w

根据(14)式，当ϵk等于w 时，可得

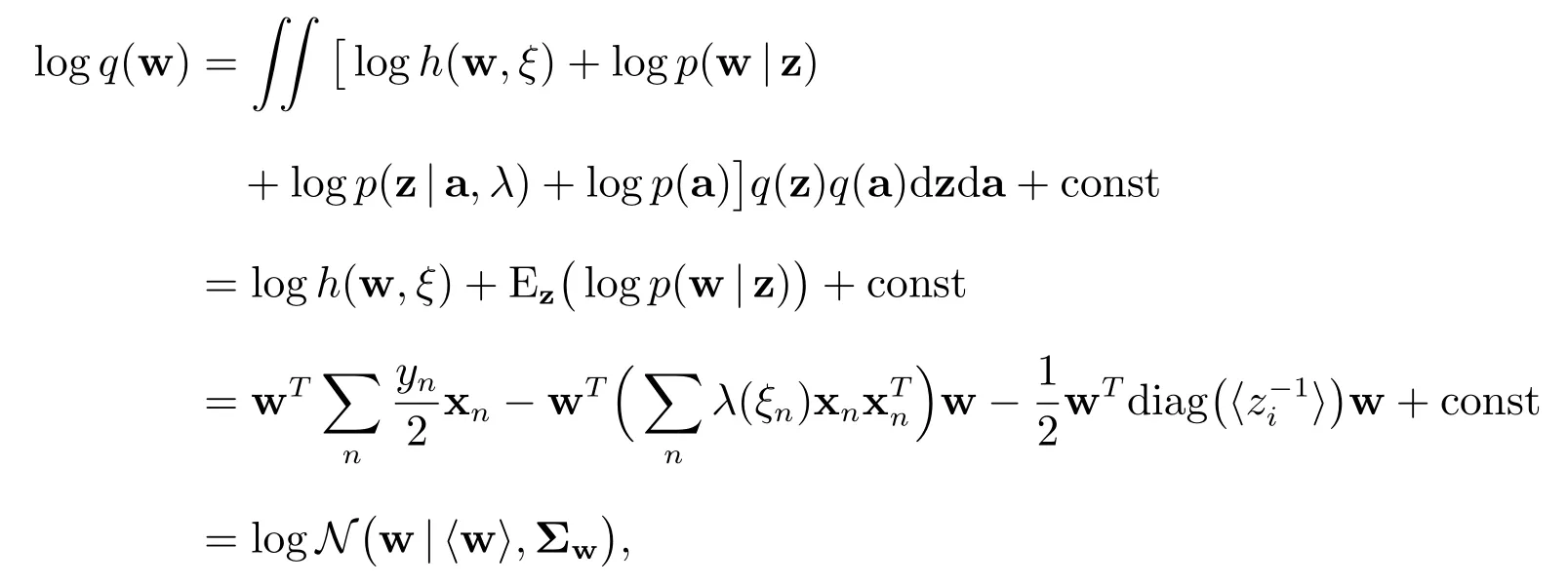
于是

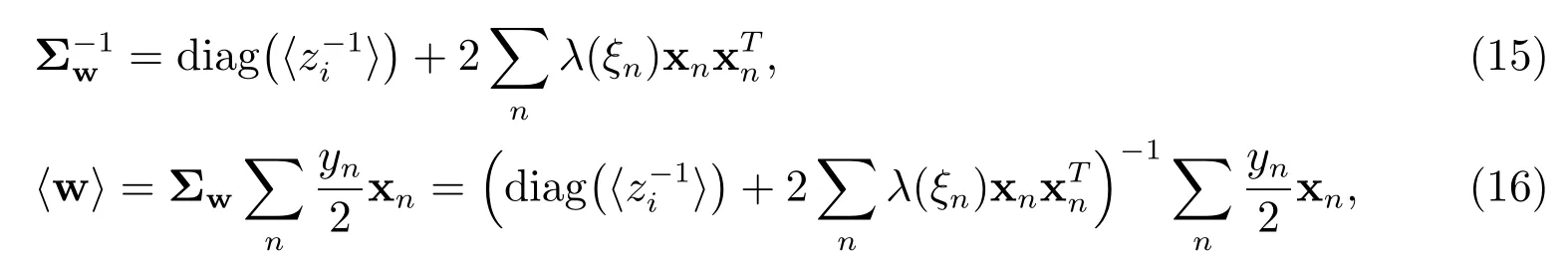
3.2 估计参数z

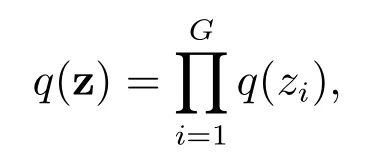
此时仅需对每个q(zi)进行估计.根据(14)式，可得zi的变分后验估计为

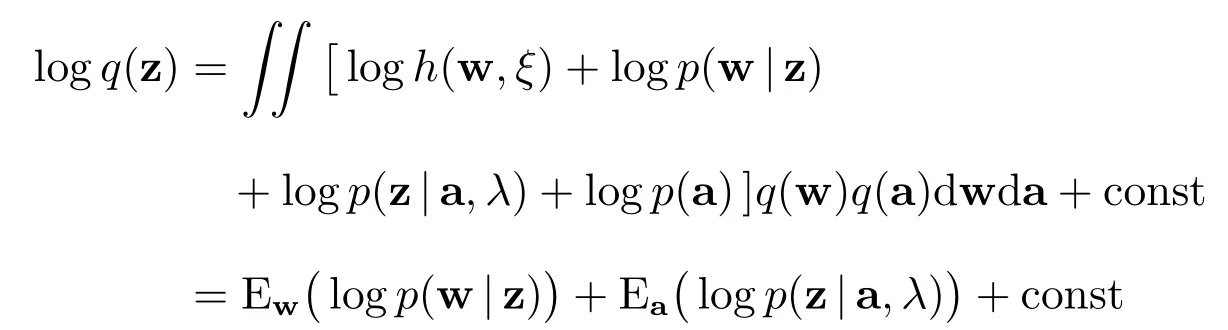
其中

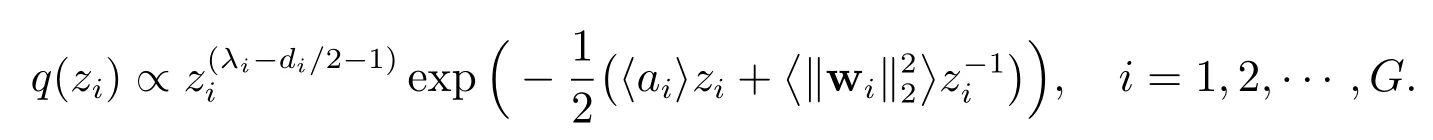
由此分布形式可知q(zi)服从广义逆高斯(GIG)分布，其期望为

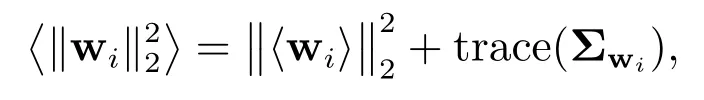
其中Σwi表示Σw中对应于第i组的子矩阵.的后验估计可通过该分布的矩[21]给出

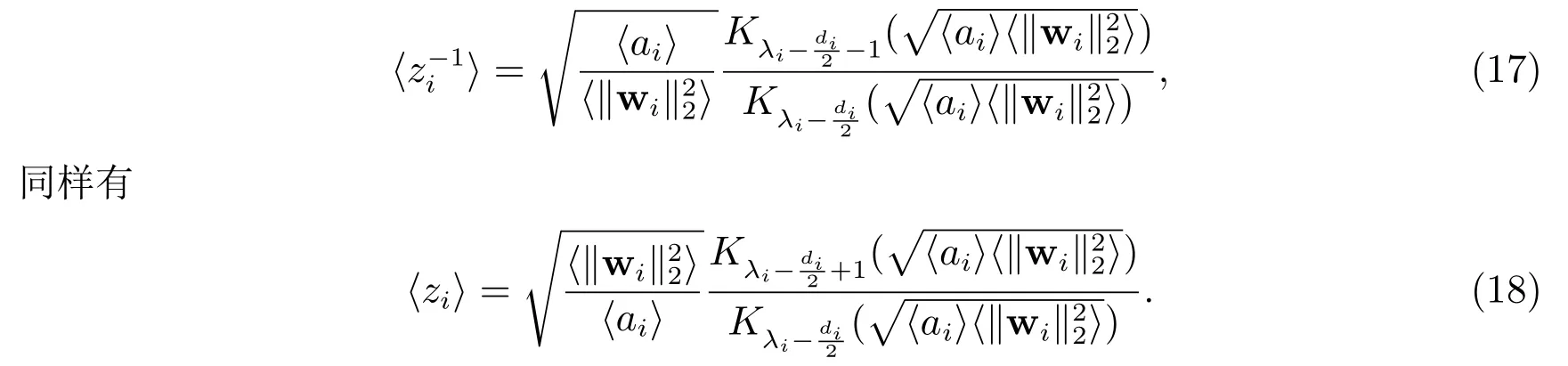
3.3 估计超参数ai与变分参数ξn

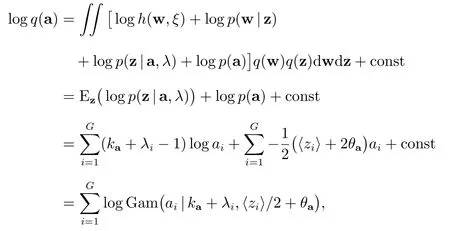
于是，ai的期望为

其中〈zi〉用(18)式计算.

对于局部参数{ξn}，由Bishop[19]可知，可以通过最大化边缘似然下界来确定，具体的更新表达式为

3.4 VBLGL算法

综上，可得

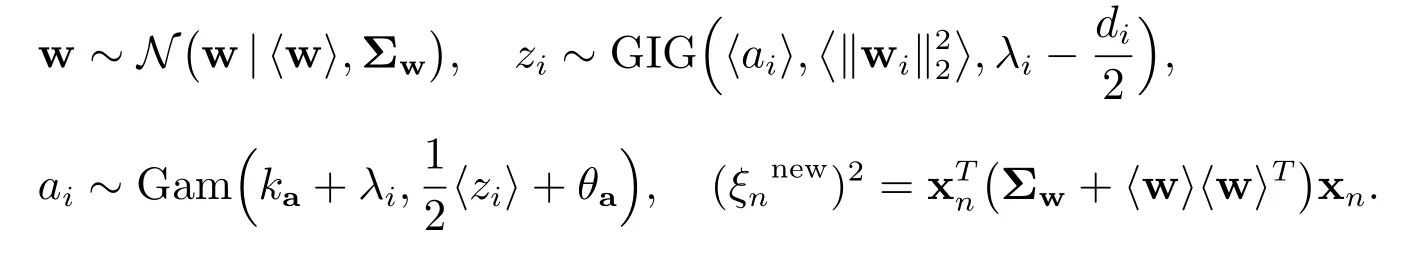
根据上述概率分布形式，通过迭代更新相关参数的矩直到满足收敛条件，可以得到有关参数的估计.在迭代过程中，全局参数ka设置为10-6，θa设置为10-6，每个λi= 1，最大迭代步数为10000 步，收敛阈值tol 为10-7.为叙述方便，简称我们算法为VBLGL(Variational Bayesian Logistic Group Lasso)，整个算法迭代过程见算法1.

算法1VBLGL 算法

步骤1初始化：ξ ∈RM,ka=10-6,θa=10-6, tol=10-7；

步骤2更新〈w〉：将Z-1和ξ值代入(16)更新〈w〉；

步骤3更新zi：用(17)更新每个重复di次，依次更新i=1,2,···,G，直到得到一个

步骤4更新ai：用(18)更新〈zi〉，并代入(19)更新〈ai〉.同上，依次更新G次得到一个a；

步骤5更新ξ：用(20)更新ξn，依次对n= 1,2,···,M进行更新，直到得到一个ξ；

步骤6重复步骤2 到步骤5，直到前后两次〈w〉差的ℓ2范数小于tol 时，迭代终止；

步骤7输出参数〈w〉以及其他参数的结果.

4 预测密度

对于新样本xn，用sigmoid 函数的下界代替数据似然P(y|X,w)，同时用回归参数w 的近似后验分布q(w)代替p(w|X,y)，可得预测密度为

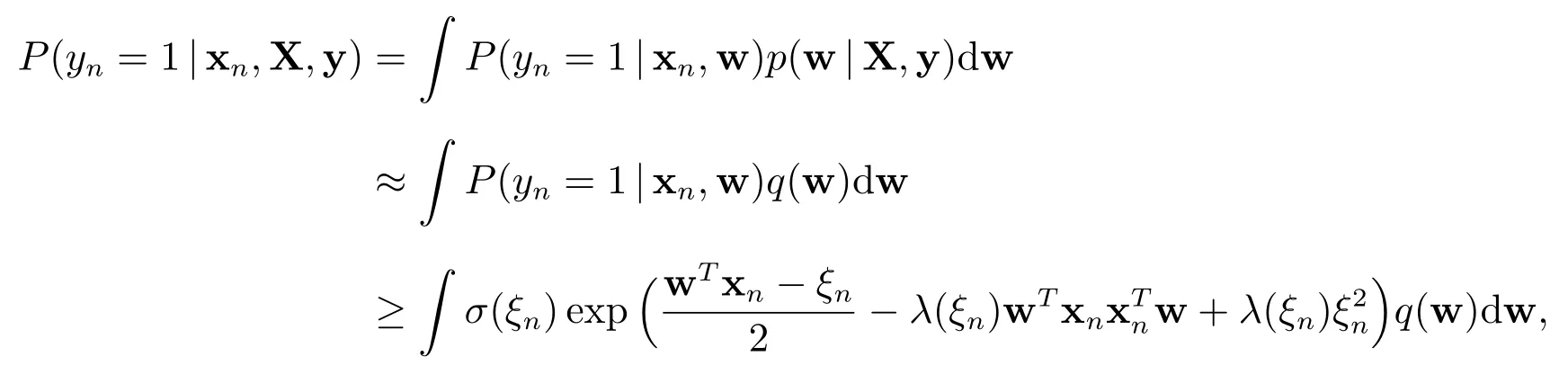
将q(w)代入上式并注意到高斯密度函数可以完全积分，可得

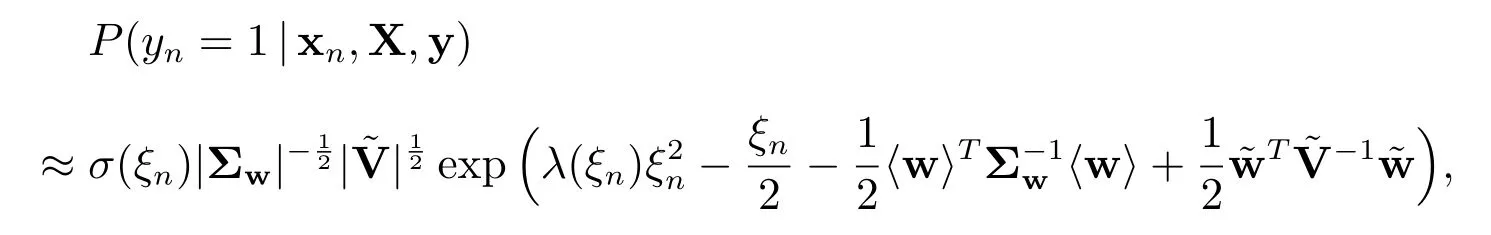
两边取对数，得

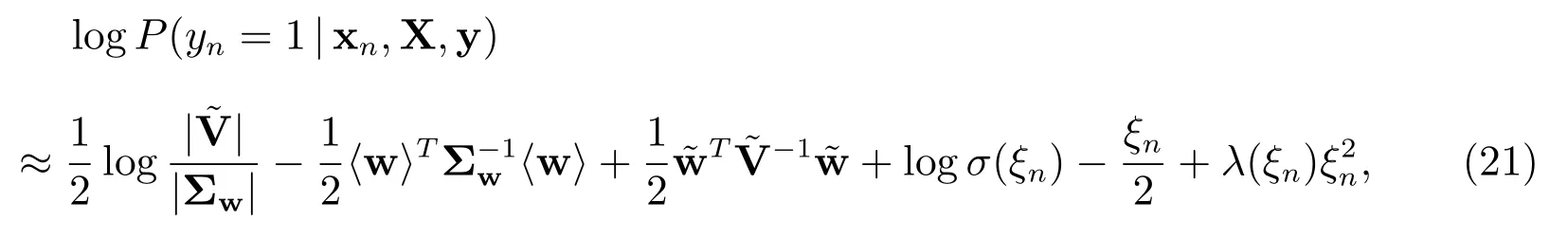
其中

在(21)中，最大化参数ξ，即可得该参数的更新公式

5 模拟实验

本节中，将通过模拟实验验证本文所提出的方法是可行的，并具有良好的预测效果.模拟实验分成两组：第一组对应协变量不分组情形，此时所有的方法都退化为解决Logistic 稀疏回归问题；第二组对应协变量分组情形，该组实验考虑Logistic 组稀疏回归问题.在第一组实验里，我们比较了Meier 等人[8]针对协变量分组的Logistic 组稀疏回归问题提出的Logistic group Lasso 方法(简记为LGL 方法)，以及Drugowitsch[22]针对协变量不分组的Logistic 稀疏回归问题提出的自动关联决策的变分Bayes 方法(简记为VBARD 方法).在第二组实验里，我们比较了LGL 方法.在这两组实验里，我们的方法都简记为VBLGL 方法.

5.1 协变量不分组情形

该部分的实验在两组不同大小的数据集上进行.第一组数据集中训练集的产生过程如下：首先，通过Matlab 中的命令rand(300,500)产生300×500 的训练集设计矩阵Xtr，该矩阵中的元素服从(0,1)区间上的均匀分布；其次，产生大小为500×1 的回归参数向量wtr，其非零元素有50 个，每个元素均服从标准正态分布；最后，通过训练集设计矩阵Xtr与回归参数向量wtr生成反应向量

不难看出，反应向量由取值为-1 或者1 的300 个输出样本构成.通过类似的方式，我们可生成样本大小为1000 的测试集，具体数据记为Xte，wte以及yte.第二组数据集的产生过程类似第一组，但训练集和测试集中样本的大小都为1000，维数仍为500.

表1 展示出三种方法在这两组数据集上10 次模拟的平均分类结果，其中mean(tr)表示在训练集上预测误差均值，mean(te)表示在测试集上预测误差均值，而std(tr)与std(te)分别表示在训练集和测试集上预测误差的标准差.如表1 所示，通过对比指标mean(tr)可以看到，所提出的方法VBLGL 取得了最小的平均训练误差.这表明，与VBARD 及LGL方法相比，VBLGL 方法具有更好的拟合性能.指标mean(te)的对比结果进一步表明，在Logistic 非分组稀疏回归问题上，VBLGL 方法相比于其他两种方法具有竞争性的表现.另外，从标准差std(tr)与std(te)指标可以看出，三种方法取得的分类结果都是比较稳定的.

表1: 协变量不分组情形下分类效果对比

5.2 协变量分组情形

在这部分实验中，考虑协变量分组情形下的分类效果.为论述方便，仅考虑等分组情形.对于组大小不相等的情形，本文所提出的方法仍然适用.协变量的维数固定为500，每10 个相邻元素为一组，总共分为50 组.非零元素组的数目记为p(亦称为“组稀疏度”).在接下来的实验中，固定组稀疏度参数p= 3.首先，产生回归系数w∈R500×1，其中在w 中有p= 3 组值非零，其他组元素值全部为零；其次，固定回归系数w 的值，按照上述5.1 节类似的方式分别产生多组不同样本大小的训练集设计矩阵Xtr与反应向量ytr，其样本大小分别为200, 300, 400, 500, 750 和1000；最后，基于回归系数w，我们生成测试样本大小为1000 的测试集设计矩阵Xte∈R1000×500和反应向量yte∈R1000×1.通过上述过程，我们得到6 组训练集和测试集.

表2 展示出两种方法，在这6 组数据集上10 次模拟的平均分类结果，其中mean(tr)，mean(te)，std(tr)，std(te)的含义如5.1 部分一致.如表2 所示，从指标mean(tr)与mean(te)上看，在数据集(1)-(6)上，VBLGL 方法在训练集、测试集上的预测误差均值均小于LGL 方法.这一现象表明，VBLGL 方法不仅具有更好的拟合精度，而且有更好的分类预测效果.另外，从标准差指标std(tr)、std(te)上来看，这两种方法所取得的分类结果都比较稳定.总体上来看，VBLGL 方法比LGL 方法更加稳定.这一现象是合理的，因为VBLGL 方法的概率化建模和参数的自动学习可以提高算法的稳定性.

6 总结与展望

针对Logistic 组稀疏回归问题，本文在Bayes 概率框架下建立了参数估计的新模型，并基于变分Bayes 方法导出参数的后验推断公式和新样本的概率预测公式.与建模Logistic 组稀疏回归问题的优化方法进行比较，本文提出的方法具有模型可解释性、参数的自动估计以及估计量拥有概率解等良好性质，而且模拟实验结果进一步表明所提出的方法具有更好的分类预测效果.在未来的工作中，我们拟将本文所提出的方法推广到多分类的Logistic 组稀疏回归问题上.

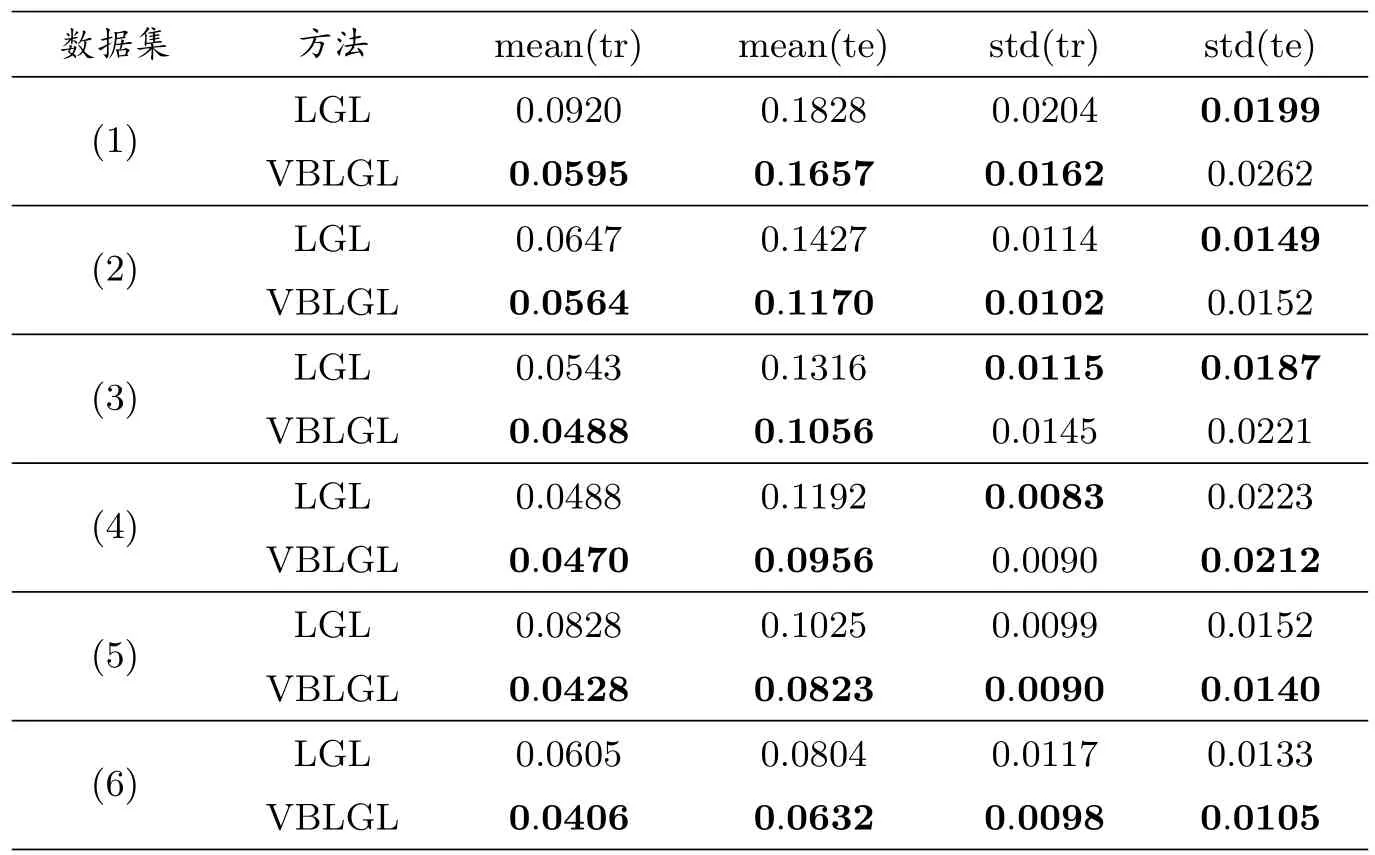
表2: 协变量分组情形下分类效果对比