带有交易成本的均值-方差-下半方差投资组合模型

王晓琴, 高岳林,2,

(1- 北方民族大学数学与信息科学学院，银川 750021;2- 宁夏智能信息与大数据处理重点实验室，银川 750021)

1 引言

为了迎接金融市场的新挑战，许多学者和投资者在Markowitz 的理论基础上发展了现代投资组合理论.在现代金融学理论中，投资组合优化问题就是研究理性的投资者怎样将自己的资金分配到几种不同的资产上以期获得最大可能收益的同时能承受尽可能小的风险.然而，经典的Markowitz 投资组合管理模型往往忽略了金融市场上一些实际存在的摩擦因素，如交易成本的考虑等.在现实中，无论是买入还是卖出证券都需要支付交易费用，忽略交易成本往往会导致无效的资产组合.因此，王春峰等[1]在投资组合管理模型的基础上引入了典型的交易成本并进行了实证分析，结果表明考虑交易成本的投资组合所获得的收益要小于不考虑交易成本的投资组合所获得的收益.康志林[2]考虑到交易费用对投资者的投资绩效具有直接影响，因此，在文中考虑了交易费用、投资比例的上界以及不允许卖空等约束的情形.任大源等[3]运用凸规划相关理论与Kuhn-Tucker 条件求解了同时含有交易成本和机会成本的投资组合选择模型.房成德等[4]以条件风险价值(CVaR)作为对风险度量的同时考虑了交易费用.Fu 等[5]考虑了在均值方差投资组合模型同时含有风险资产和无风险资产，且把整个投资过程划分为两个阶段.Mansini 等[6]在本文中考虑了带有线性交易成本的投资组合模型，文中所考虑的模型是一个混合整数规划模型.Najafi 和Mushakhian[7]在文中考虑了交易成本，并且用方差和条件风险价值的线性加权来度量投资组合的风险.Yue 等[8]用进化算法求解了考虑交易成本和流动性的双目标投资组合优化模型.王婧等[9]运用蚁群算法解决了股票投资组合优化问题.李继和高岳林[10]用均值衡量投资组合的收益，用风险价值(VaR)度量投资组合的风险并用改进后的差分进化算法求解了投资组合选择问题.毕晓君和王佳荟[11]把教与学算法和差分进化算法进行了融合，以解决算法容易陷入局部最优的问题.目前，投资组合中风险的度量方法已有好几种，如：方差、下半方差、绝对偏差，风险价值(VaR)和条件风险价值(CVaR)以及他们之间的一个加权组合等等都用来度量投资组合的风险.本文用方差和下半方差的加权组合来度量投资所带来的风险.因此，建立了带有交易成本的均值-方差-下半方差投资组合模型，并运用教与学算法对提出的模型进行了求解.本文内容安排如下：第1 节给出了考虑交易成本的均值-方差-下半方差投资组合模型；第2 节给出了求解模型的教与学算法设计；第3 节给出了实证分析；第4 节给出了本文的结论.

2 考虑交易成本的均值-方差-下半方差投资组合模型

2.1 目标函数

本文只考虑证券市场上存在的n种风险资产.

x= (x1,x2,···,xn): 其中xi表示第i种资产的投资比例；ui: 表示第i种资产投资比例的上界；Ci: 表示组合中第i个风险资产在[0,T]时间内的交易费率；Ri: 表示组合中第i个风险资产在[0,T]时间内的收益率；Rit: 表示第i个风险资产在第t个时期的收益率，其中表示在[0,T]时间内的组合收益率，假设随机变量的期望值可以用历史收益的均值来近似表示，即

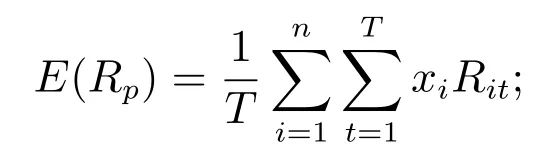
根据投资组合的理论，目标函数有两个：最大化投资组合的收益，最小化投资组合的风险

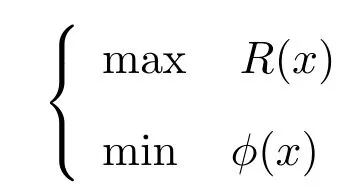
2.2 模型的建立

1) 均值-方差-下半方差投资组合选择模型

根据投资组合理论，投资者偏好收益而厌恶风险.因此，一般情况下，投资者总是在一定的预期收益率下，希望投资组合的风险最小，基于均值-方差-下半方差投资组合选择模型建立如下

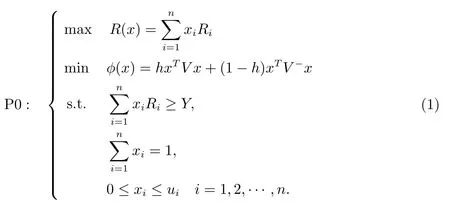
在P0 中，约束条件一表示投资者有某个能够接受的最低期望收益率Y；约束条件二表示投资到每一种资产的比例之和为1；第三个约束条件表示资产不允许卖空且第i种资产投资比例不超过ui，则P0 的经济含义就是在满足以上三个约束条件的前提下，怎样分配资产的投资比例，在风险达到最小的情况下，使得投资组合获得最大的收益.

2) 考虑交易成本的均值-方差-下半方差投资组合选择模型

投资过程中，交易成本是不能忽略的.在实际的证券交易中，总存在着交易成本的问题，且交易成本对投资的收益有较大的影响，从而决定投资组合的最终收益.因此，在模型中考虑交易费用是非常必要的.这里考虑的交易成本函数表现为资产交易量具有两个拐点的非凸非凹函数，如图1 所示，称之为“典型交易成本函数”.

BIM技术具有三维可视化的特点，是对建筑及构件的直观表达。所见即所得的方式提高了理解和沟通的效率，降低了二维图纸阅读的专业性要求，对于复杂的空间关系，如复杂管线、体型复杂建筑等来说优势明显，如图2所示。

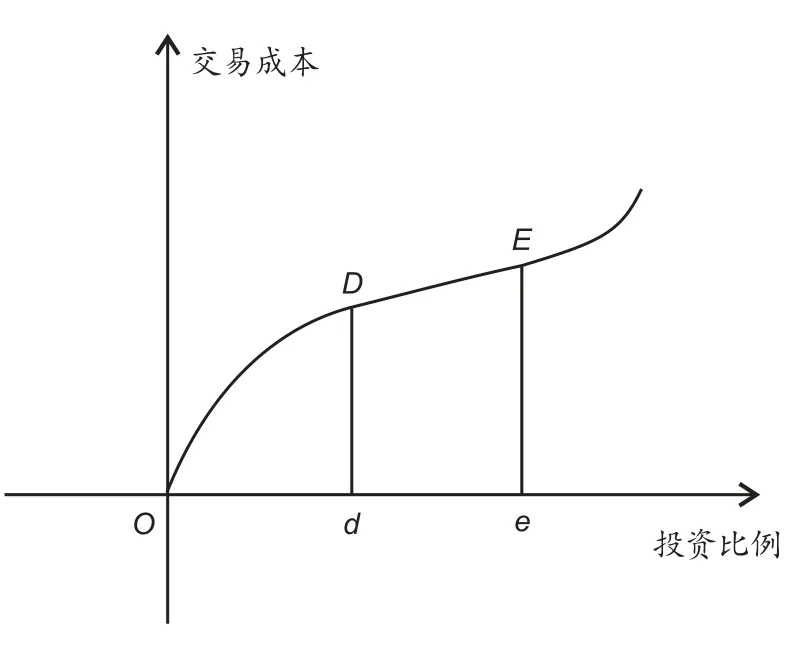
图1: 交易成本函数图

当购买资产量比较小时，交易效率较低，所以单位交易成本很大，随着购买资产量的上升，单位交易成本将逐渐减少，故在达到D点之前，交易成本函数C(X)是上凸的.然而，当越过D点后单位交易成本已经达到最优，所以单位交易成本函数C(X)基本保持不变，直到到达E点，也就是说DE段交易函数是线性的.如果购买资产量继续增加，越过E点后，由于证券市场上资产供给不足等因素使得对应资产的单位交易成本逐渐变大，所以交易成本函数C(X)在越过E点后将变成下凸的.记每次交易时的成本函数为C(X)，则成本函数的表达式如下[4]

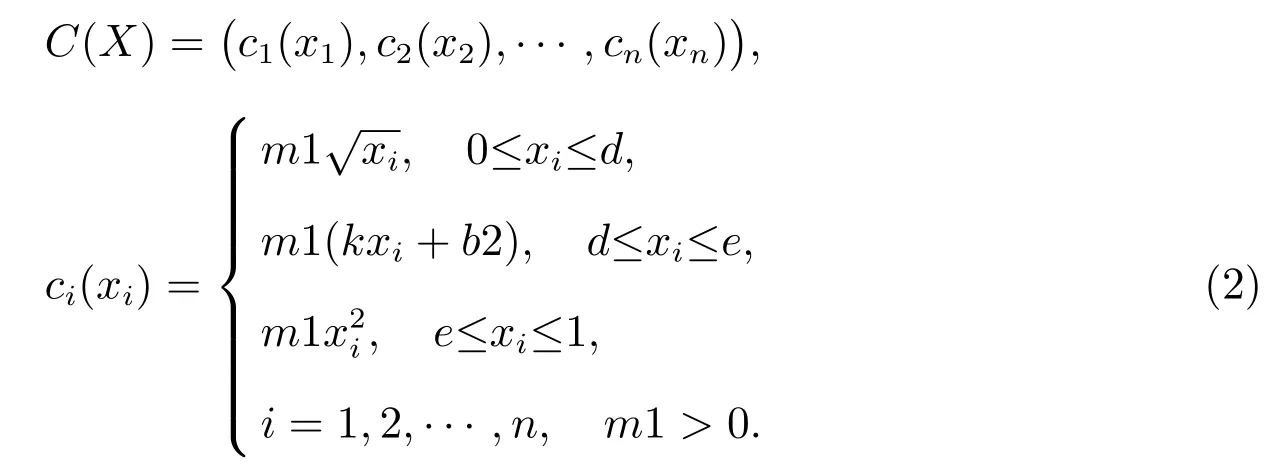
因此，考虑交易成本的均值-方差-下半方差投资组合选择模型为

为了更好的实现风险和收益之间的均衡，考虑同时优化两个目标，我们引入风险厌恶系数A(0＜A ＜1)[12]，其中A反映投资者的风险偏好，A值越大，投资者越注重收益.反之，投资者更注重对风险的控制，转化后的模型如下

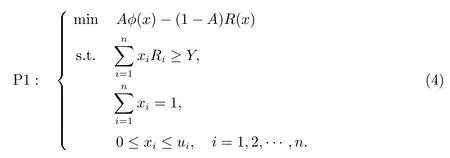
3 求解模型的教与学算法设计

教与学优化算法就是一种以班级为单位的教学过程进行仿真模拟的优化算法，搜索空间中的每个种群代表每个班级，种群的规模也就是每个班级里的人数，决策空间的维度就是学生所要学习的科目，每个学生的学习水平就代表目标函数中的适应度值，种群中适应度值最好的个体确定为老师.教与学优化算法主要包括”教师对学生的教学”和”学生之间的相互学习”两个阶段，通过这两个阶段的共同努力来提升全班同学的平均水平.

3.1 需要求解的问题

本文所建立的是一个带有约束的双目标优化问题，即最大化收益和最小化风险这两个目标.为了简化计算，把双目标的问题转化为一个最小化单目标的问题，把有约束的优化问题转化为一个无约束的优化问题.如果计算所得目标函数值越小，说明构建的投资组合相对越好.

3.2 教与学优化算法[13]

a) 教师阶段

教师(适应度值最优的个体)根据全班学生(种群)的平均水平运用以下三个公式对全班学生(种群个体)进行教学过程：

令i=1:N为种群的规模

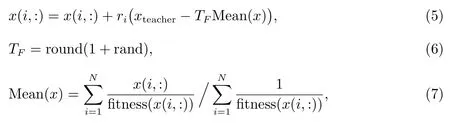
其中ri为[0,1]之间的随机数，xteacher为教师个体，即当前种群的最优粒子位置，TF为教学因子，一般取1 或2.round 表示对计算结果四舍五入取整，rand 取0-1 之间的随机数.Mean(x)是班里所有学生知识水平的平均值，由公式(7)确定.fitness 表示求适应度函数.

b) 学生阶段

学生在老师进行教学阶段之后，为了进一步提升自身的水平，与班里的其他学生按照以下公式进行继续学习.

令i=1:N;j=1:N，其中N为种群的规模，且

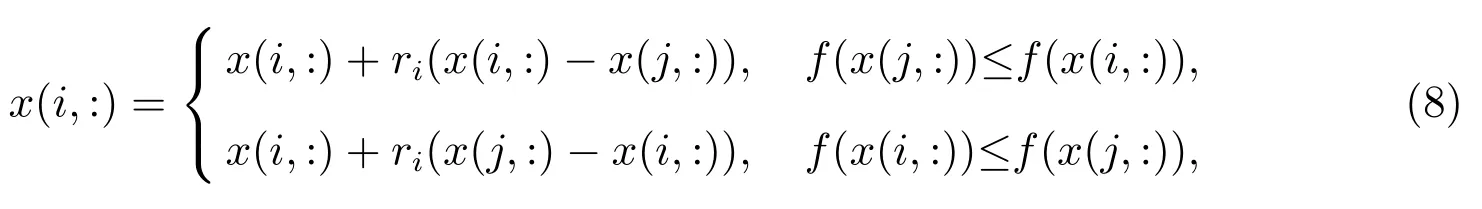
其中x(j,:)为当前种群中第j个粒子的位置，其中f(x(i,:))和f(x(j,:))分别为第i个粒子和第j个粒子的适应度值.

3.3 教与学优化算法流程

步骤1种群初始化及参数设置.包括初始种群的规模N，最大迭代次数M，搜索空间维数D，决策变量范围(lbi,ubi)以及其他相关的参数；

步骤2在搜索空间中初始化每个学员，并计算每个学员所学学科的综合成绩(适应度值)，把综合成绩最好(适应度值最优)的学员确定为xteacher，因为文中所求的目标函数为最小化的问题，所以计算的适应度值越小越好；

步骤3利用公式(7)求班里所有学员所学课程成绩的均值Mean(x)，也就是求搜索空间中所有粒子的均值Mean(x)；

步骤4利用公式(5)和(6)执行教学阶段，从而对粒子x(i,:)的位置进行更新，并计算相应的适应度值；

步骤5利用公式(8)执行学生之间的相互学习阶段，从而更新粒子位置x(i,:)，并计算适应度值，执行选择操作；

步骤6利用公式(2)计算每种风险资产的交易成本；

步骤7如果达到所设定最大迭代次数，输出最优解，否则返回步骤2.

4 实证分析

4.1 模型的转化

运用罚函数法将有约束的单目标问题转化为无约束的单目标问题来求解，转化以后的等价模型为

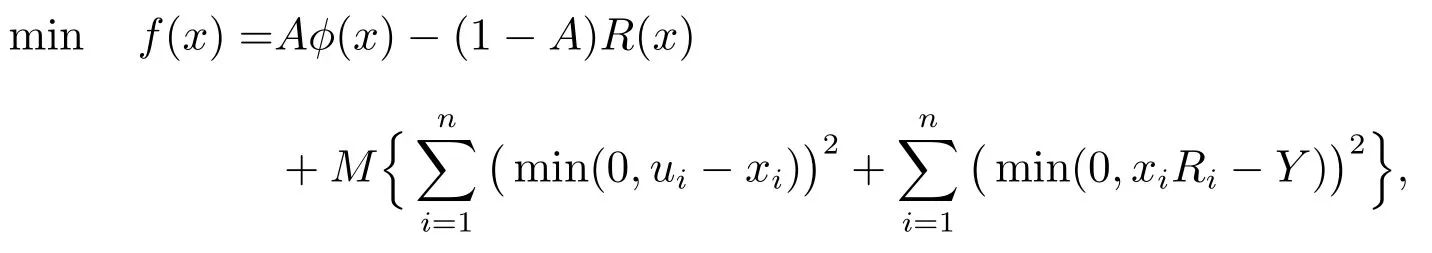
其中M是一个充分大的正数.

4.2 数值算例

本节针对本文的理论结果及算法给出了数值算例.假设对表1 中的8 支股票进行投资组合，种群规模N为60，每只股票的投资比例小于等于0.6，交易成本函数中的m1 = 0.1,a= 0.3,b= 0.4，独立运行120 次，利用教与学的Matlab 程序进行编码实现，得到给定期望收益下的目标函数值、最小风险以及最优投资比例，如表2 所示.

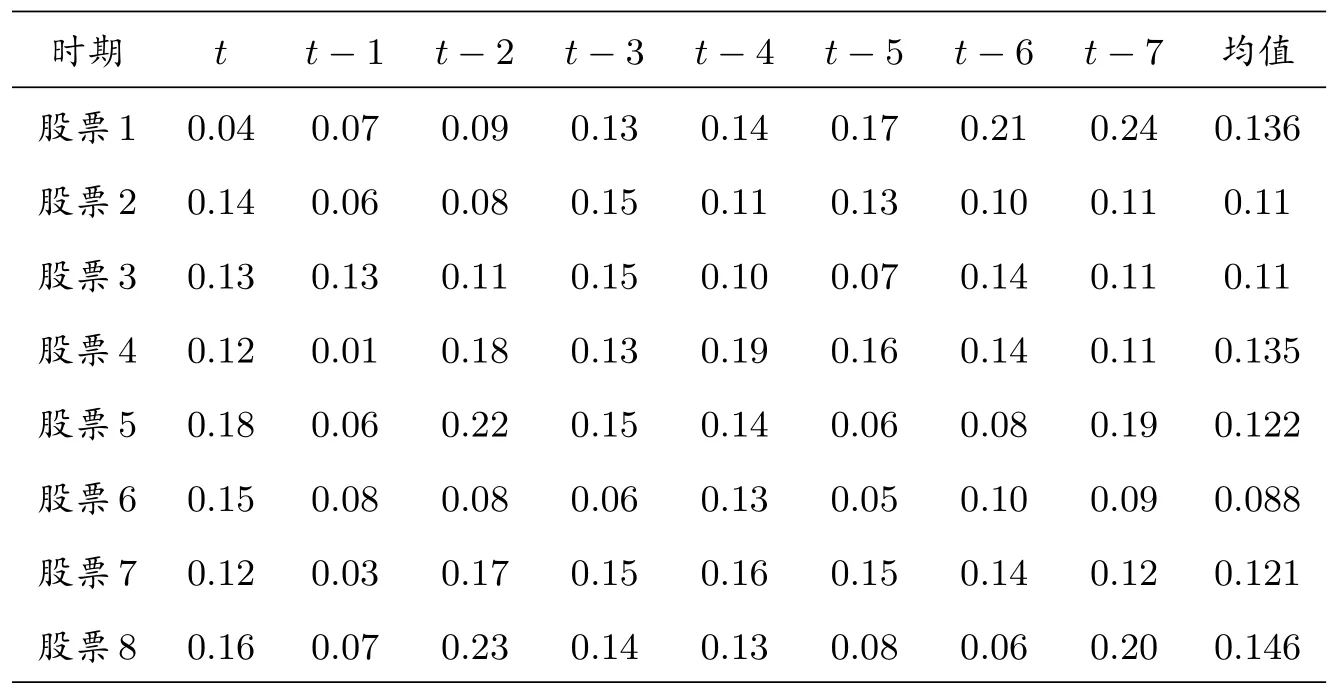
表1: 股票的收益和均值

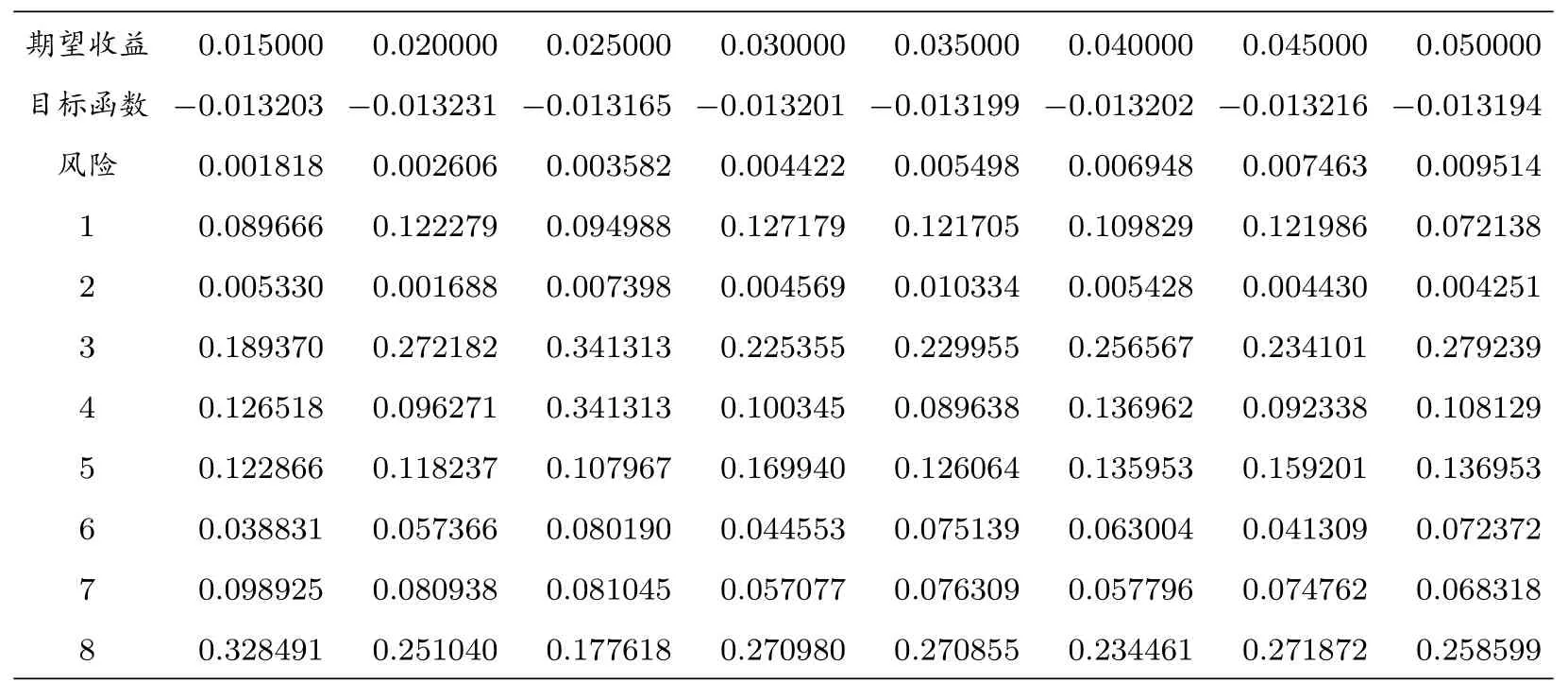
表2: 不同期望收益下的最优投资组合

从表2 可以看出，投资组合的目标风险随着给定期望收益率的增加也在不断地增加，符合证券市场上的实际情况.投资者若想得到较高的收益，则对第3 种和第8 种股票的投资比例相对增加，此时资产组合的风险也会相应的增加.所以，投资者应该结合自身的实际情况，设定符合自己实际的预期收益率.

图2 为投资组合的有效前沿[14]，可以看出给定相同的期望收益率，考虑交易成本时的风险总比忽略交易成本时的风险大，此时的投资比例也有所不同.此外，当期望收益率较低时，二者的风险差别不显著，随着收益率的增加，考虑交易成本的风险值增加较快，超过一定范围后则相对稳定，充分体现了交易成本在投资组合中的价值[10].

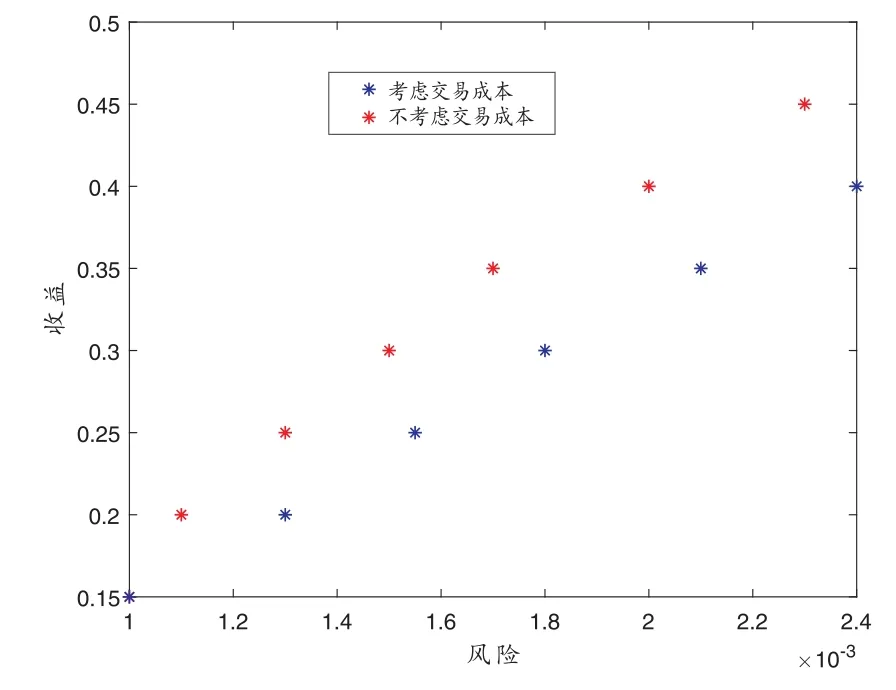
图2: 有效前沿图

4.3 算法优越性比较

为了说明教与学优化算法的优越性，在风险厌恶系数分别为A= 0.1,A= 0.3,A=0.5,A= 0.7 的情况下，把教与学优化算法与粒子群算法在同等条件下迭代了120 次进行了对比，如图3 所示.

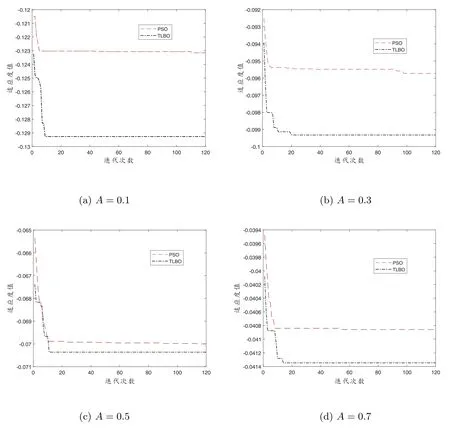
图3: 不同风险厌恶系数下两种算法的比较

从图3 中的四个图片中可以看出，在不同的风险厌恶系数下，教与学优化算法的收敛性都优于同等条件下的粒子群优化算法.

5 结论

本文是在典型交易成本函数的基础上，建立了含有典型交易成本函数的均值-方差-下半方差的投资组合模型，并采用教与学优化算法对提出的模型进行了求解.最后，进行了实证研究.通过研究发现新建的模型可以说明投资组合风险和收益之间的关系，为投资者决策提供了重要依据，并在不同的风险厌恶系数下，把教与学优化算法和粒子群算法进行了比较.