基于Min(N,D,V)-策略和单重休假的M/G/1排队系统队长分布的瞬态和稳态解

王 敏, 唐应辉

(四川师范大学数学科学学院，成都 610068)

1 引言

根据实际背景和应用的需要，在平衡顾客等待时间的同时也为了降低系统成本，从而增加系统的收入，学者们在研究经典排队系统的同时，提出并研究了许多休假排队模型和有控制策略的排队模型，取得了较丰硕的成果[1-23]，大大拓宽了早期排队论的研究和应用领域.经典的休假策略有服务员的单重休假、服务员的多重休假和多级适应性休假等，而经典的控制策略有T-策略、D-策略和N-策略等.随着研究的深入，一些把服务员休假与控制策略相结合的排队模型也得到了学者们的关注，例如把N-控制策略与服务员单重(多重)休假相结合，就产生了N-策略单重休假排队模型、N-策略多重休假排队模型，以及具有休假中断机制的Min(N,V)-策略休假排队模型.从管理和成本的角度，当生产和制造的环境发生较大改变时，系统想要转换成另一种控制策略，但大多数情况下，由于成本的原因要抛弃现有的硬件系统设施是不可能的，于是学者们把N-策略和D-策略等结合起来就提出了二维混合控制策略的排队模型，如Min(N,D)-控制策略的排队系统模型[15]，并且在这些方面的推广研究也取得了较好成果[10-21].

文献[15]研究的具有Min(N,D)-控制策略的排队系统模型，其主要模型特征是把N-策略与D-策略有机结合起来，不仅分析了系统的排队性能指标，而且在建立费用结构的基础上，用数值计算例子讨论了系统的二维最优控制策略，并与单一的N-策略和D-策略进行了比较分析，说明了混合控制策略优于单一的控制策略.本文在此基础上，把服务员的休假机制引入其中，提出一种服务员可休假且在休假时间中根据Min(N,D,V)-控制策略可立即中断休假的M/G/1 排队模型，即具有Min(N,D,V)-控制策略和服务员单重休假的M/G/1 排队模型：每当系统变空时，服务员就去休假(或去做辅助性工作，以增加系统的收入).如果在假期中到达的顾客数达到N个或者到达的顾客数所需服务时间总量超过D(D ≥0)，服务员马上结束休假并开始为顾客服务.这种假期中断机制对于控制系统队长是有益的，而且可以克服系统频繁转换所带来的费用问题，对系统的优化具有重要意义.本文应用更新过程理论和全概率分解知识，借用拉普拉斯变换工具，分析了在任意初始状态条件下系统队长的瞬态分布和稳态分布特征，得到了队长瞬态分布解的拉普拉斯变换表达式和方便计算稳态队长分布数值解的递推表达式，从而进一步给出了稳态队长的随机分解结果和附加队长分布解的显示表达式，使我们更清楚地了解到该排队模型的结构.

本文研究服务员具有单重休假，而且在休假中根据Min(N,D,V)-策略可中断休假的M/G/1 排队系统，其模型刻画如下：

1)M/G/1 型排队模型[23]：相邻两个顾客之间的到达是相互独立的，其每个间隔时间τ有分布F(t)=1-e-λt，每个顾客的服务是相互独立的，其每个顾客的服务时间χ有任意分布G(t)，且设平均服务时间为1/µ(0＜µ＜∞)；

2) 服务员采取单重休假机制和系统采取Min(N,D,V)-控制策略：每当系统变空时，服务员马上开始一次随机时间长度V的休假，且休假时间V服从任意分布V(t).但是，服务员在休假时间中根据Min(N,D,V)-控制策略可立即中断休假，即在服务员的休假期间，如果系统中到达的顾客数达到了N个(N ≥1，事先设定的正整数阈值)，或者到达系统等待服务的顾客所需服务时间总量不小于D(D ≥0，事先设定的实数阈值)，无论哪一个先发生，处于休假期的服务员立即结束休假回到系统中为顾客服务(在这种情况下，服务员的实际休假时间长度达不到约定的休假时间长度V)；如果在服务员的休假期间系统中有顾客到达，但到达数没有达到N个，且到达系统等待服务的顾客所需服务时间总量也小于D，则等到此次休假结束后服务员再回到系统中，且立即为在现场的顾客服务；如果服务员此次休假结束时系统中仍没有顾客，则服务员留在系统中直到有顾客到达并立即服务；

3) 随机变量τ、χ和V是相互独立的，而且假设在t= 0 时刻，如果系统是空的，则不采取该休假机制和控制策略，服务员留在系统中等待顾客到达后立即对其进行服务(这样的假设更符合实际情况，但稳态结果与此假设无关).

2 一些符号的说明和准备

一些符号说明：N(t)表示系统在任意时刻t的队长，即时刻t在系统中的顾客数；

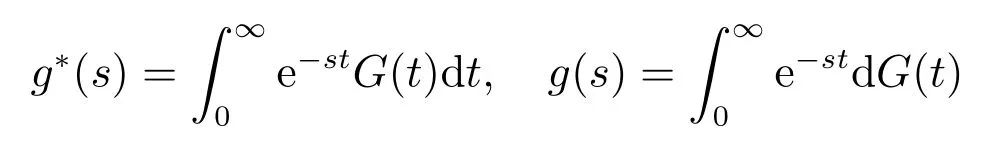
分别表示相应的G(t)关于t的拉普拉斯(L)变换和拉普拉斯-斯蒂尔切斯(LS)变换；G(k)(t)表示G(t)的k(≥1)重卷积，即

且

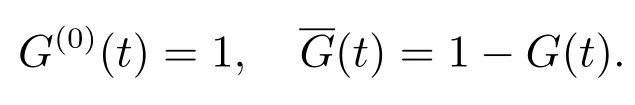
引入如下概念：

1) 系统闲期：系统连续保持空闲(无顾客)的一段时间.如果我们用表示系统第j个系统闲期的长度，则由到达过程为参数λ(λ ＞0)的泊松过程知其分布为P{≤t}=F(t)=1-e-λt,t ≥0,j ≥1；

2) 系统忙期：从第一个顾客到达空闲的系统起，直到系统再次变空为止的这段时间；

3) 服务员非忙期：从系统刚变空的时刻起，直到服务员休假结束回到系统而且开始为顾客服务的时刻为止的这段时间；

4) 服务员忙期：从服务员开始为顾客服务的时刻起，直到系统再次变空为止的这一段时间.

令b表示标准的M/G/1 排队系统中从一个顾客开始的服务员忙期(从服务员开始为顾客服务的时刻起，直到系统再次变空为止的这一段时间)，对t ≥0,ℜ(s)＞0，令

则有如下引理.

引理1[23]对ℜ(s)＞0,b(s)是方程z=g(s+λ-λz)在|z|＜1 内的唯一根，且

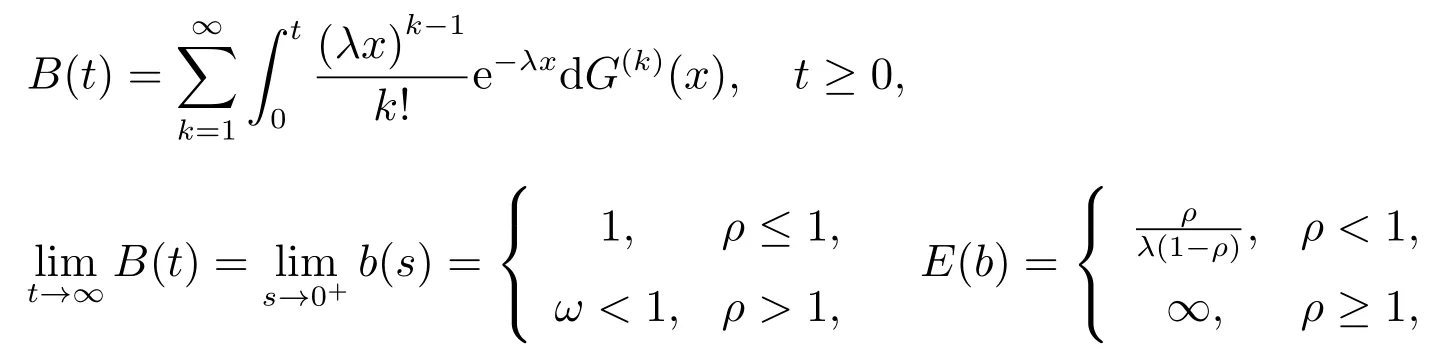
其中ω(0＜ω ＜1)是方程z=g(λ-λz)在(0,1)内的根，表示系统的交通强度，ℜ(s)表示复变量s的实部.

又令Qj(t) =P{b ＞t ≥0;N(t) =j}表示在服务员忙期b中队长为j(j ≥1)的瞬态概率，并且t= 0 时，只有一个顾客，服务员忙期b刚开始，即Q1(0) = 1,Qj(0) =0,j ＞1.

引理2[23]令

为Qj(t)的拉普拉斯变换，对ℜ(s)＞0，有

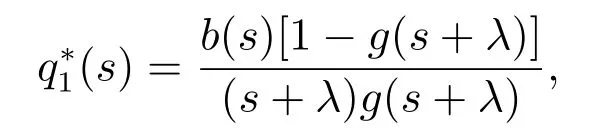
其中当j ＜0 时，有且求和

3 系统队长分布的瞬态解

令pij(t) =P{N(t) =j|N(0) =i}表示初始时刻有i个顾客的条件下，时刻t队长为j的瞬态概率，

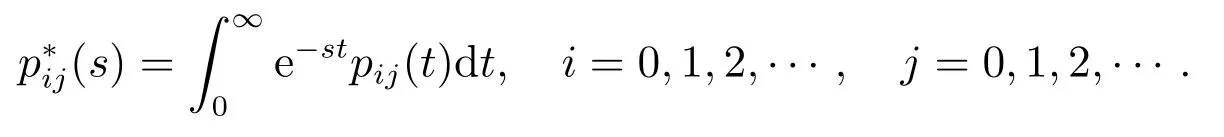
定理1对ℜ(s)＞0，有

其中

当求和的上标小于下标，即k ＜i时，求和下同.

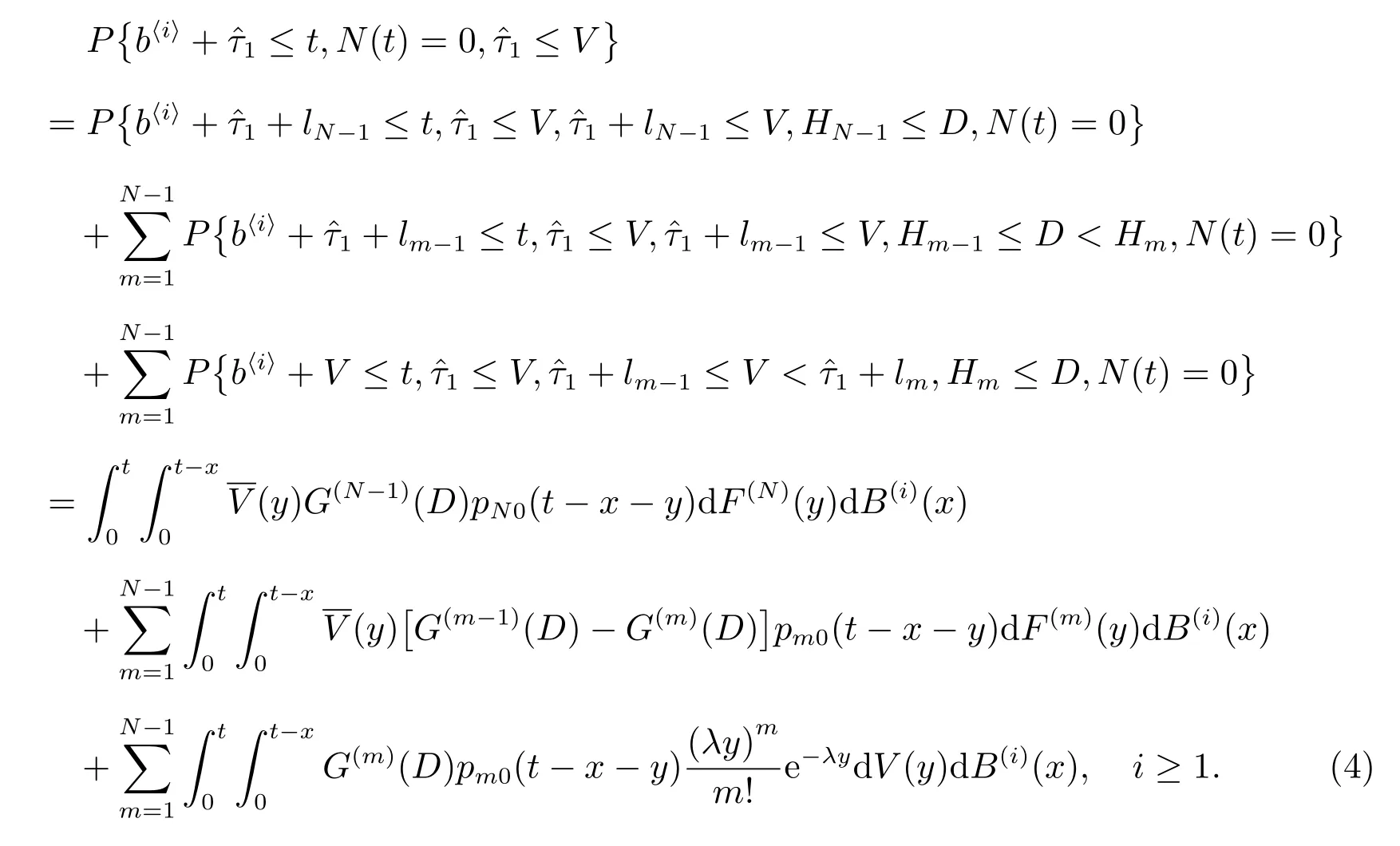
上第(3)式的第三项为

对(3)-(5)式作L 变换，有

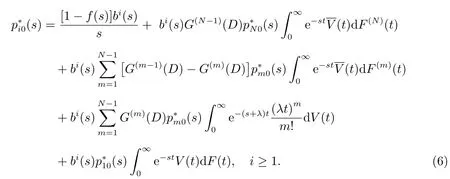
在N(0) = 0 初始条件下，根据模型假设中第3)条：在初始时刻系统中无顾客时服务员不休假，系统也不采取Min(N,D)-控制策略，所以

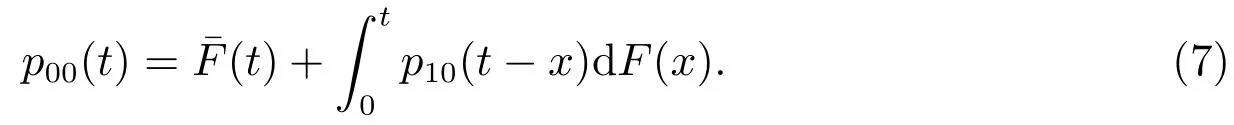
对(7)式作L 变换得到

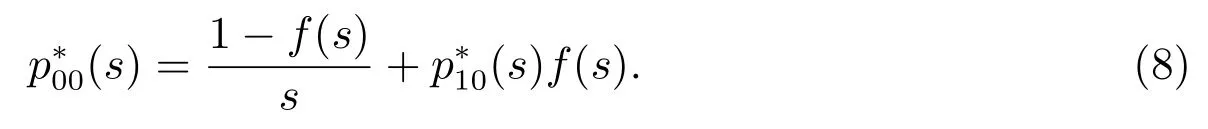
在(6)式中，取i=1，结合(8)式可得

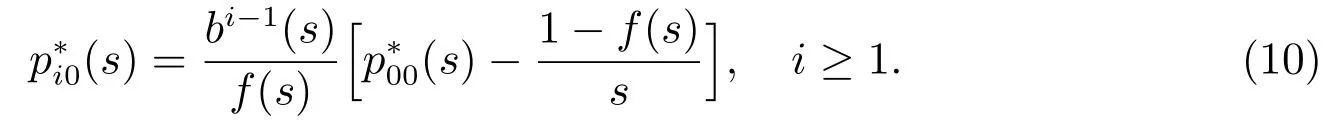
注1当N=1 或D=0 时，本文研究的排队系统等价于文献[23]讨论的服务员无休假的经典M/G/1 排队系统，所以下面对N=1 或D=0 的情况不再讨论.

定理2当N ≥2 且D ＞0 时，对ℜ(s)＞0，有：

1) 当j=1,2,···,N-1 时

2) 当j ≥N时

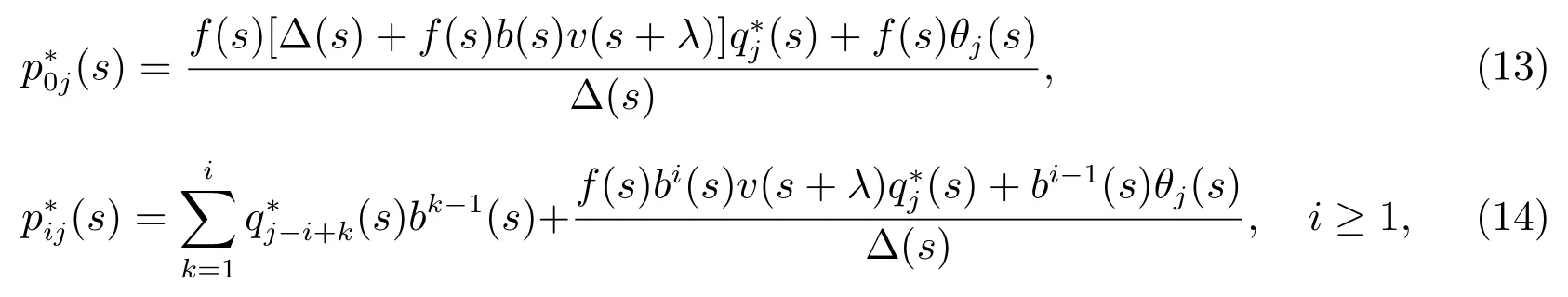
其中

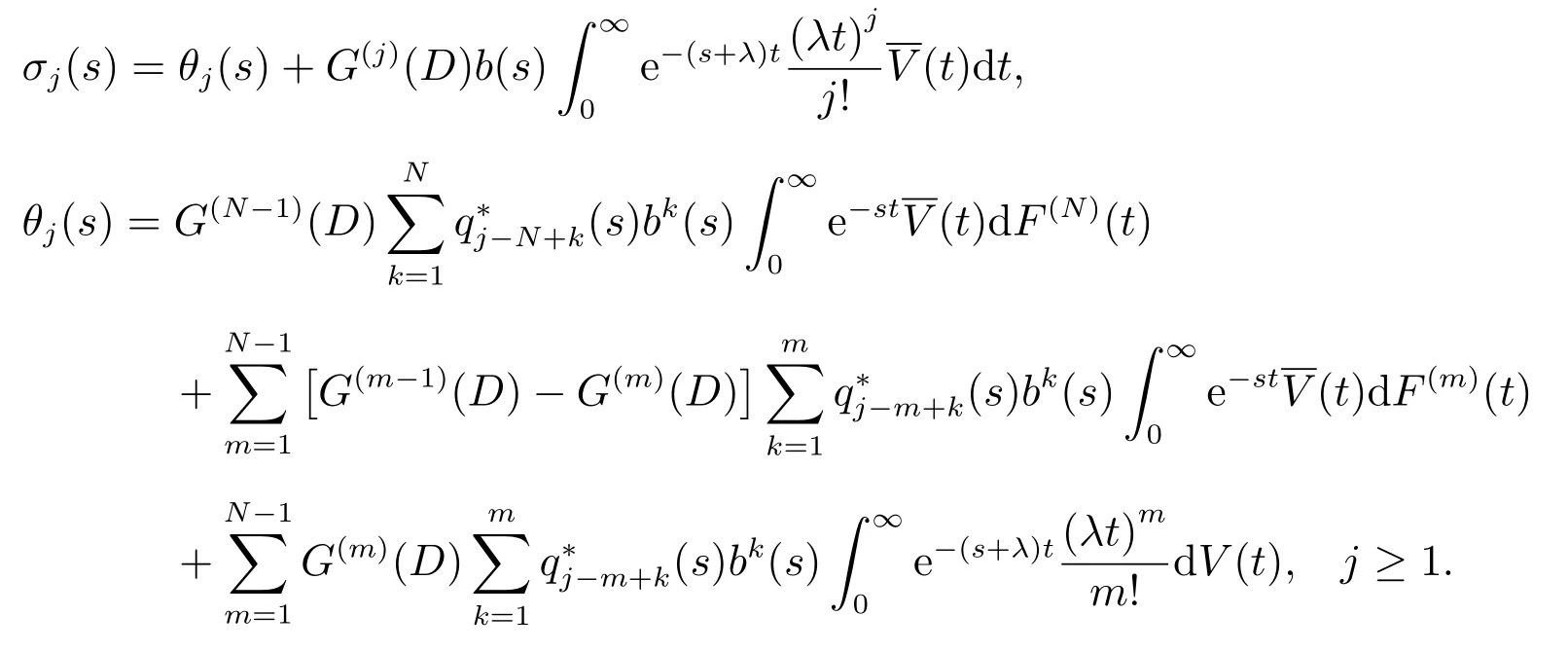
证明 当j=1,2,···,N-1 时，因为“在时刻t队长为j”可分为如下两种情形.

情形1“时刻t落在服务员假期中且队长为j”.

情形2“时刻t落在服务员忙期中且队长为j”.

所以，当i ≥1，类似定理1 的分解，得

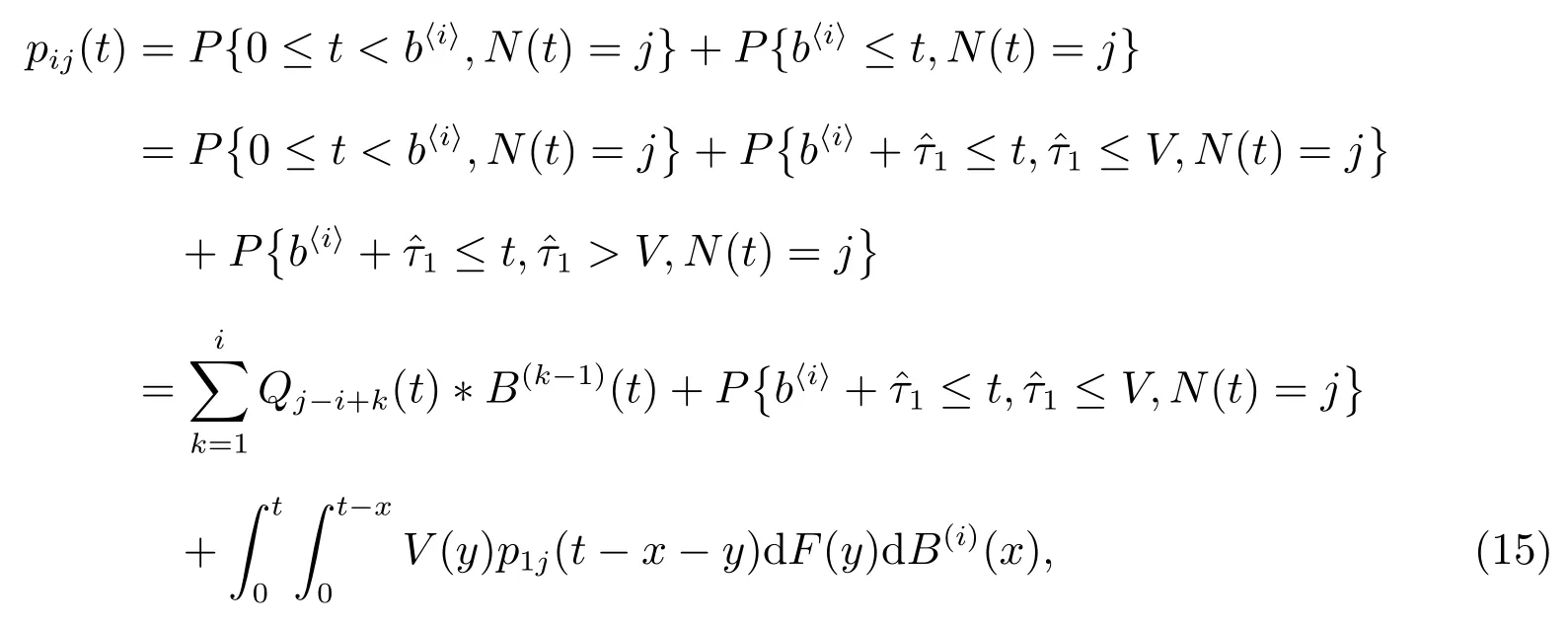
其中

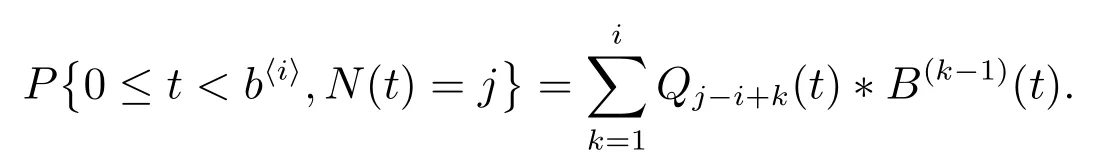
(15)式的第二项为

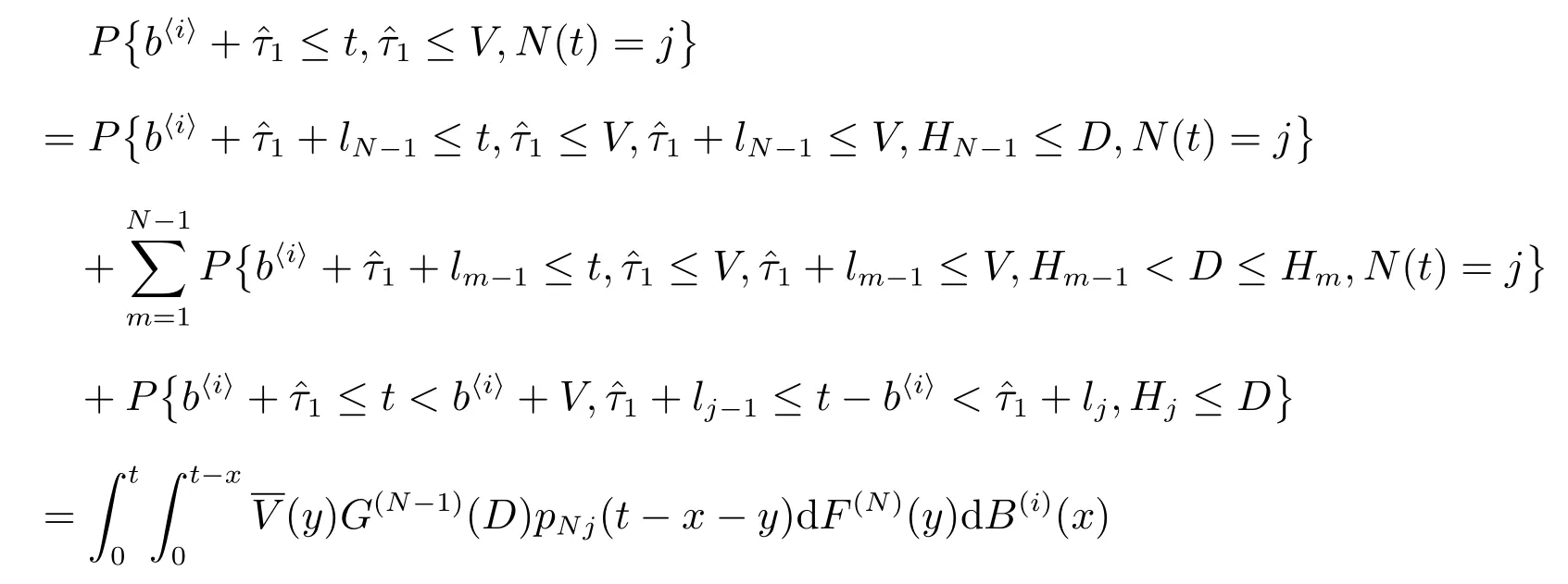
把(16)式代入(15)式作L 变换，可得

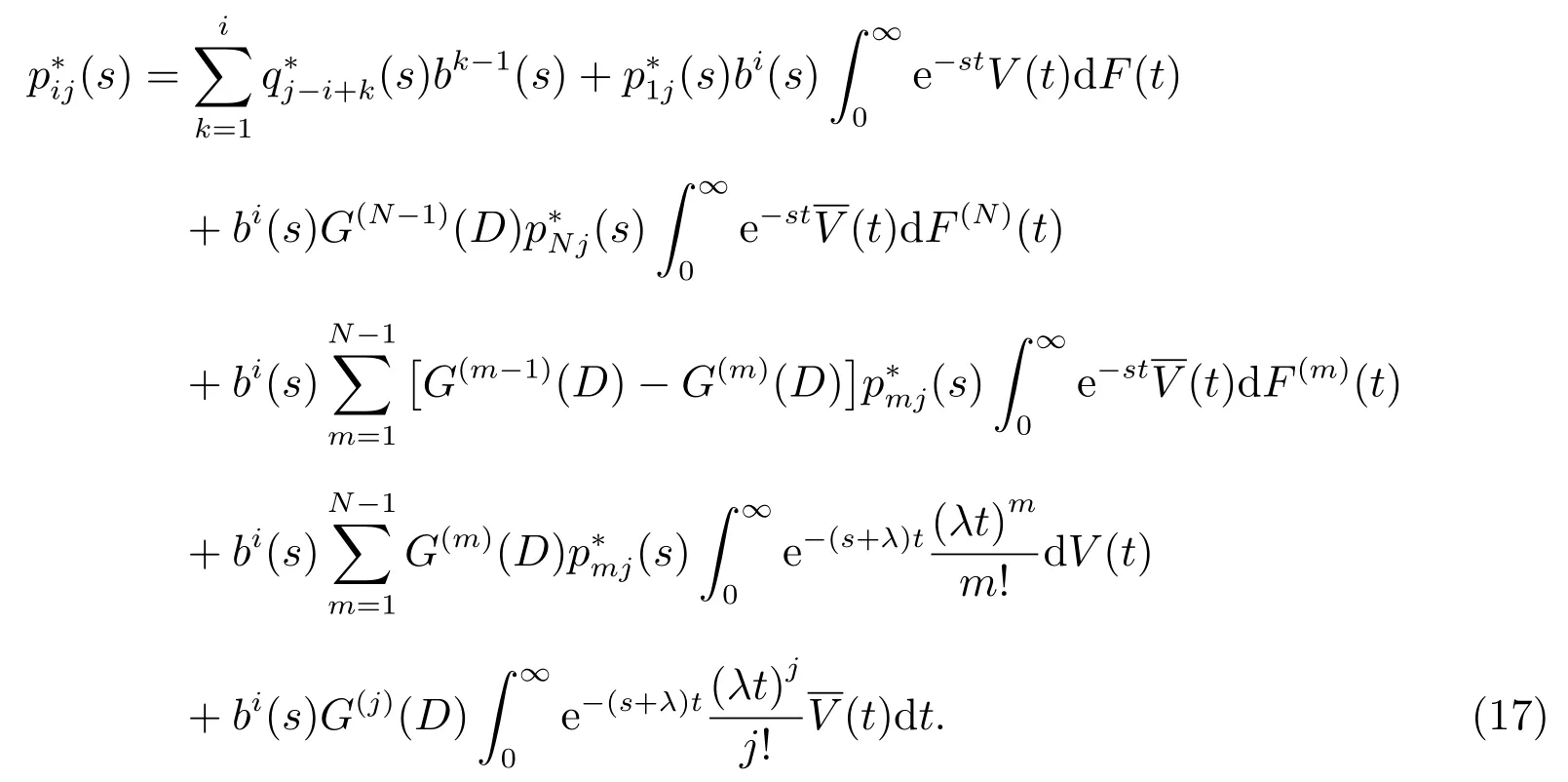
同理可得

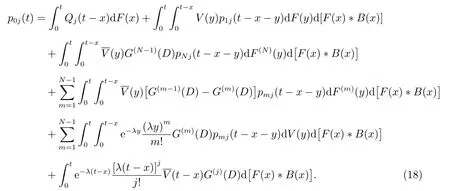
对(18)式作L 变换得到

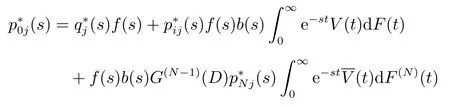
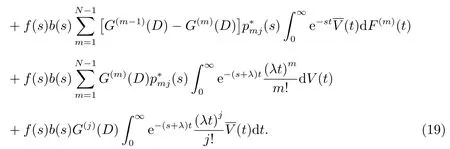
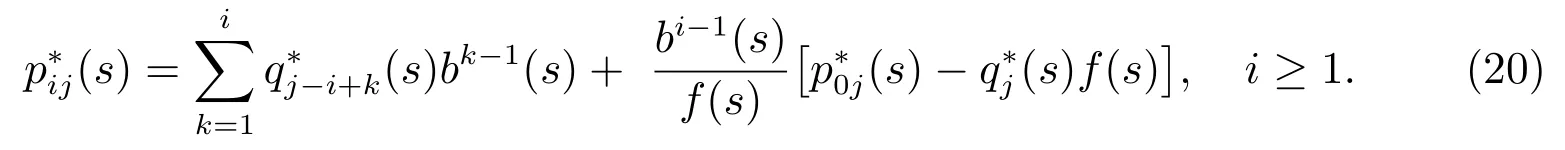
当j ≥N时，在时刻t队长为j当且仅当时刻t落在服务员忙期中且队长为j，于是当i ≥1 时，使用全概率分解技术，同理可得

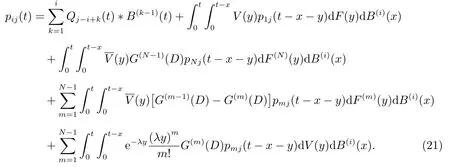
余下的推证过程完全仿照j=1,2,···,N-1 时的推导过程.

4 系统队长分布的稳态解及稳态队长的随机分解结构

定理3令j=0,1,2,···，则：

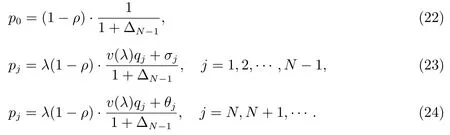
此时{pj,j=0,1,2,···}构成概率分布，其中

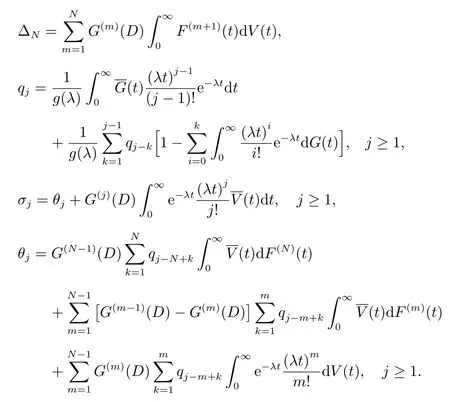
证明 由

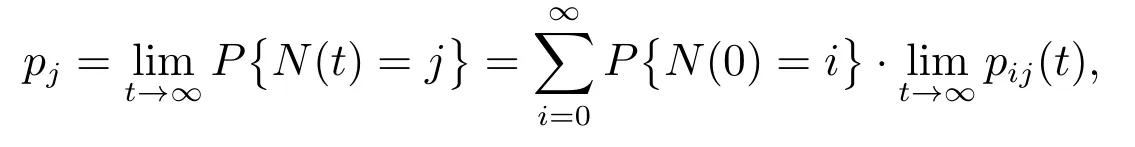
而

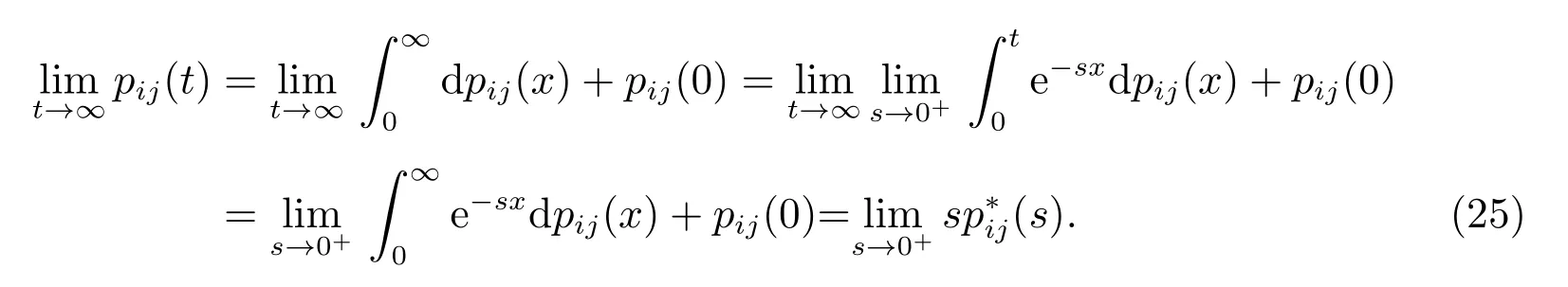
当j=0 时，有

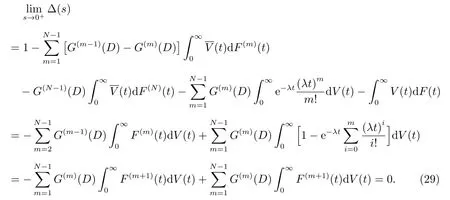
1) 当ρ ＞1 或ρ=1 时，有

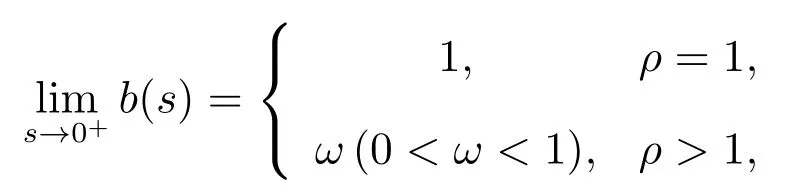
且E(b)=∞，而

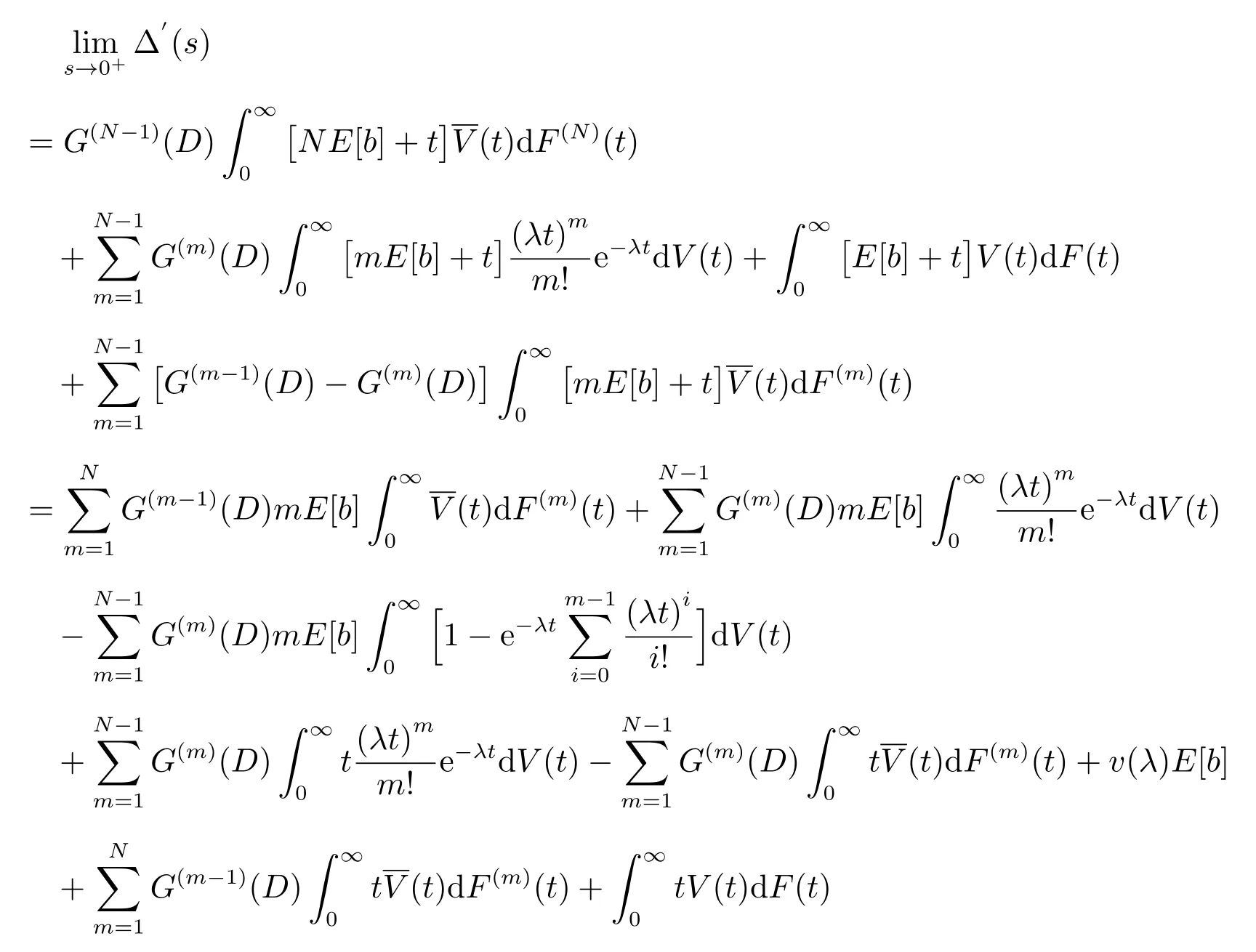
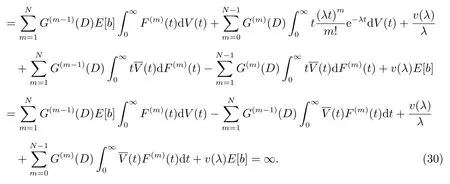
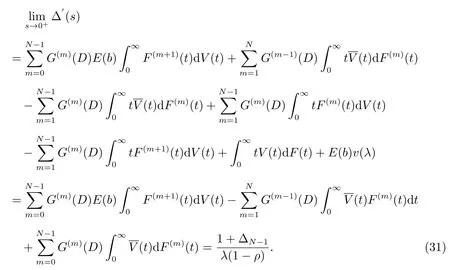
于是使用洛必达法则，可得

对于j ≥1，结合(11)-(14)式，使用洛必达法则，完全仿照p0的推导过程可得.

由于

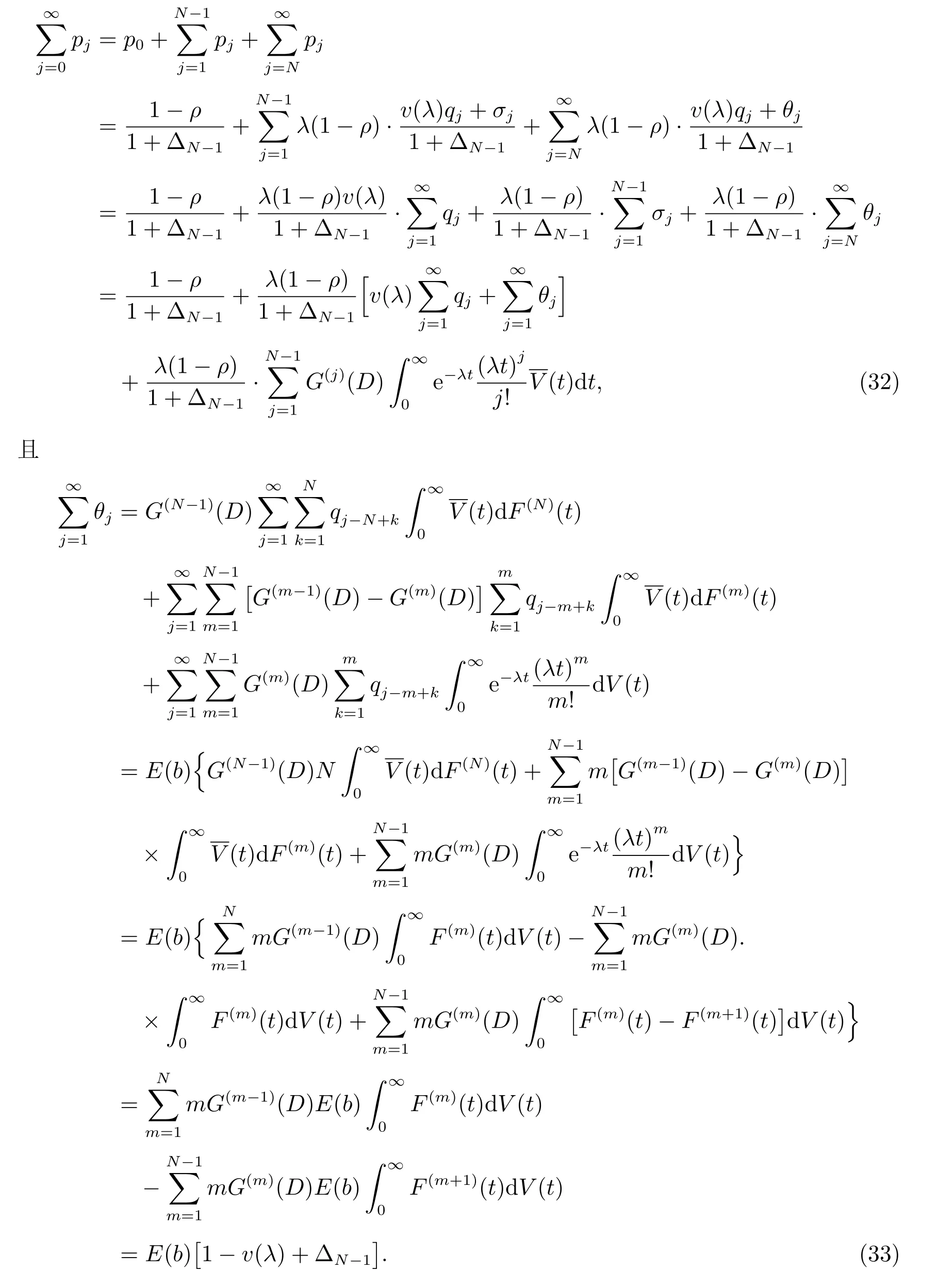
经计算可得

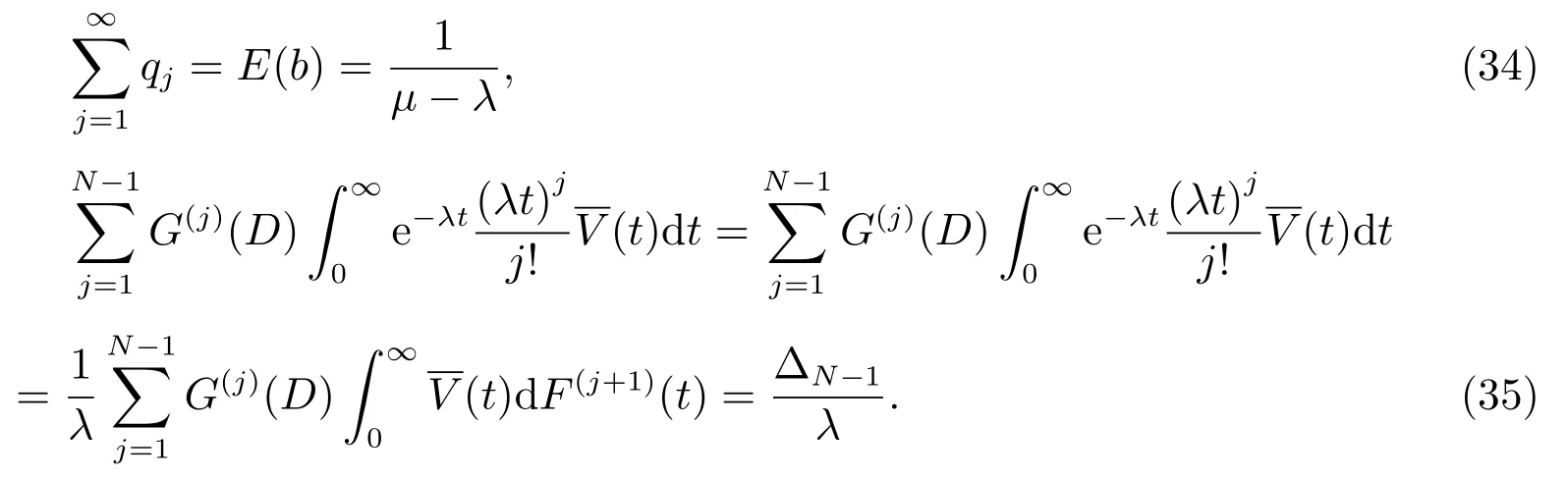
将(33)-(35)式代入(32)式，整理即可证明.

定理4(稳态队长的随机分解结构) 令P(z)表示该系统稳态队长分布的概率母函数，当ρ ＜1 时，有

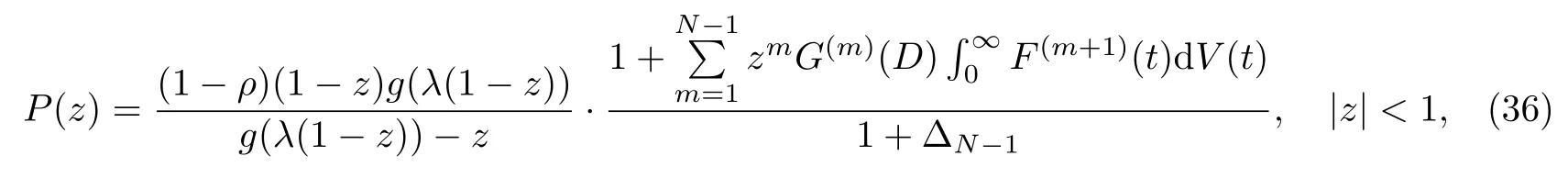
且平均队长为

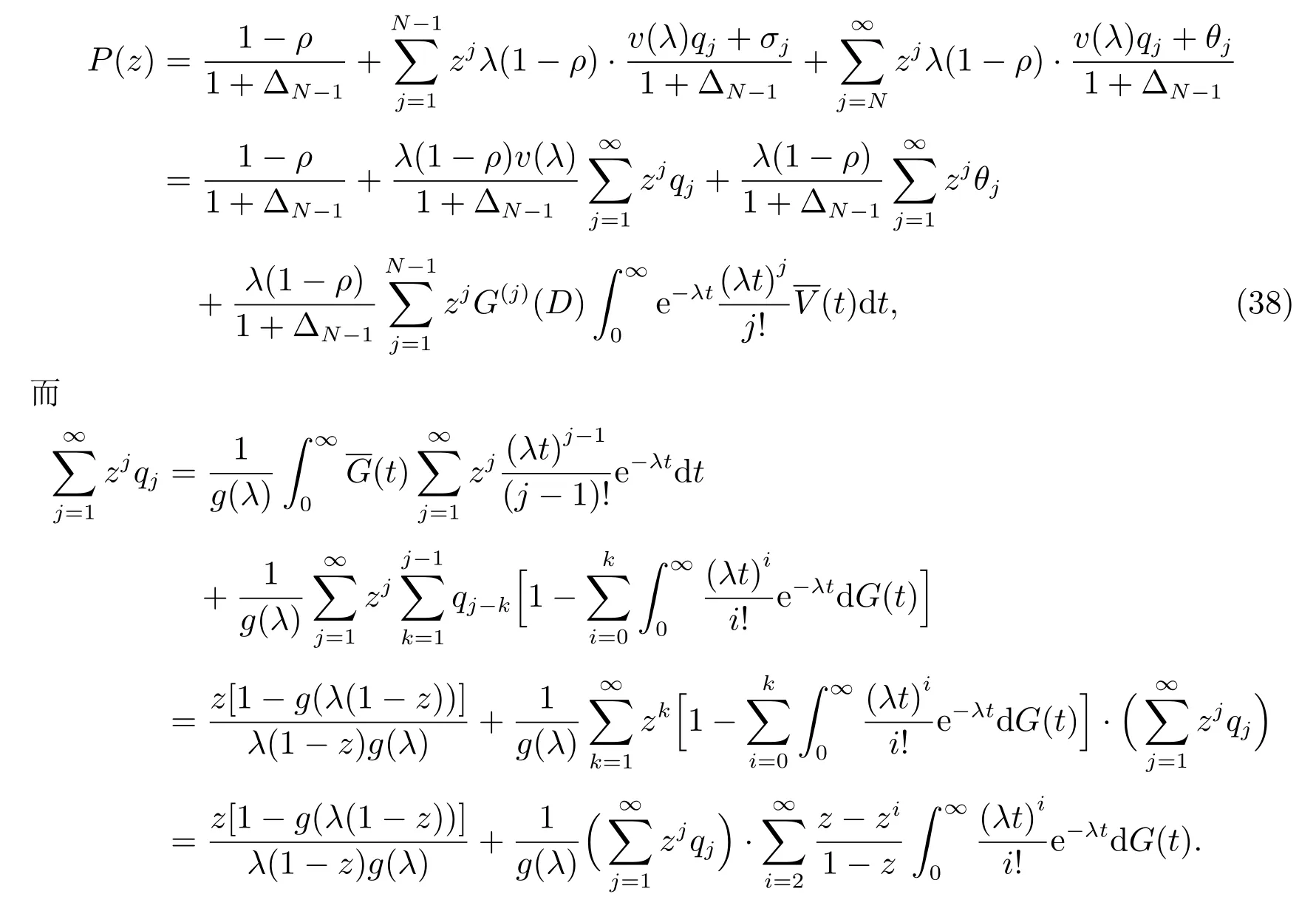
于是

定理5本文研究的基于Min(N,D,V)-策略和单重休假的M/G/1 排队系统的稳态队长可分解成独立的两部分之和：一部分是文献[23]中的经典M/G/1 排队系统的稳态队长，另一部分是由服务员单重休假机制和Min(N,D)-策略引起的附加队长Ld，且附加队长有如下离散分布

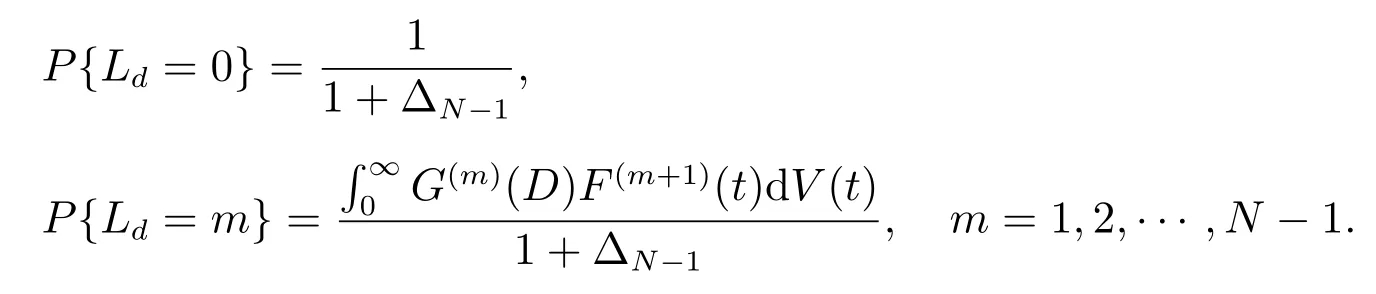
证明 由上面(37)式可知本文研究的排队系统的稳态队长可分解为独立的两部分之和.下面求附加队长Ld的离散分布.令

其中

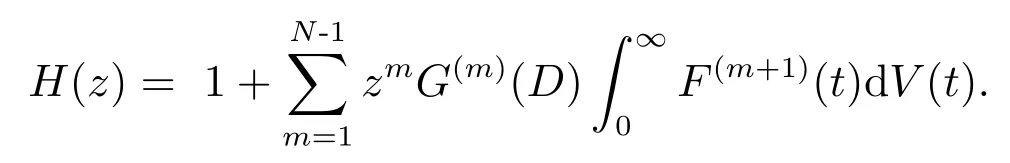
然后利用

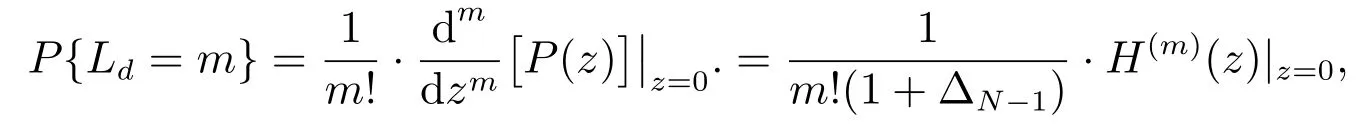
经过计算整理可得，这里H(m)(z)表示H(z)关于z求m(m= 1,2,···,N- 1)阶导数，H(0)(z)=H(z).

5 一些特殊情形

推论1当P{V=T} = 1 时，即服务员事先约定的休假时间是一个固定时间长度T(T ＞0).对ρ ＜1，有

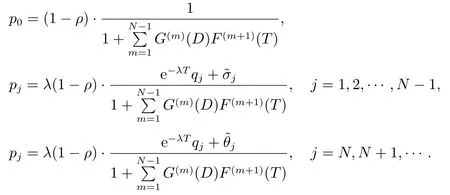
系统稳态队长分布的概率母函数为

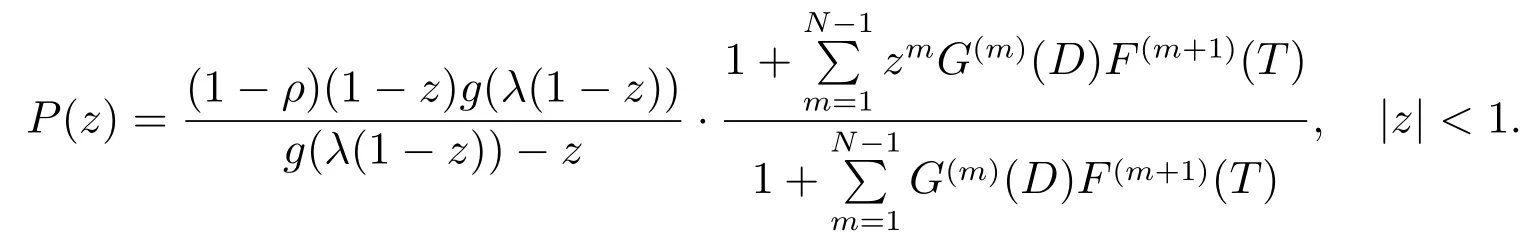
平均队长为

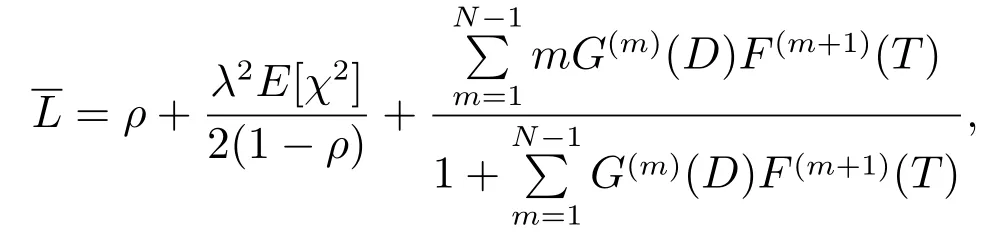
其中

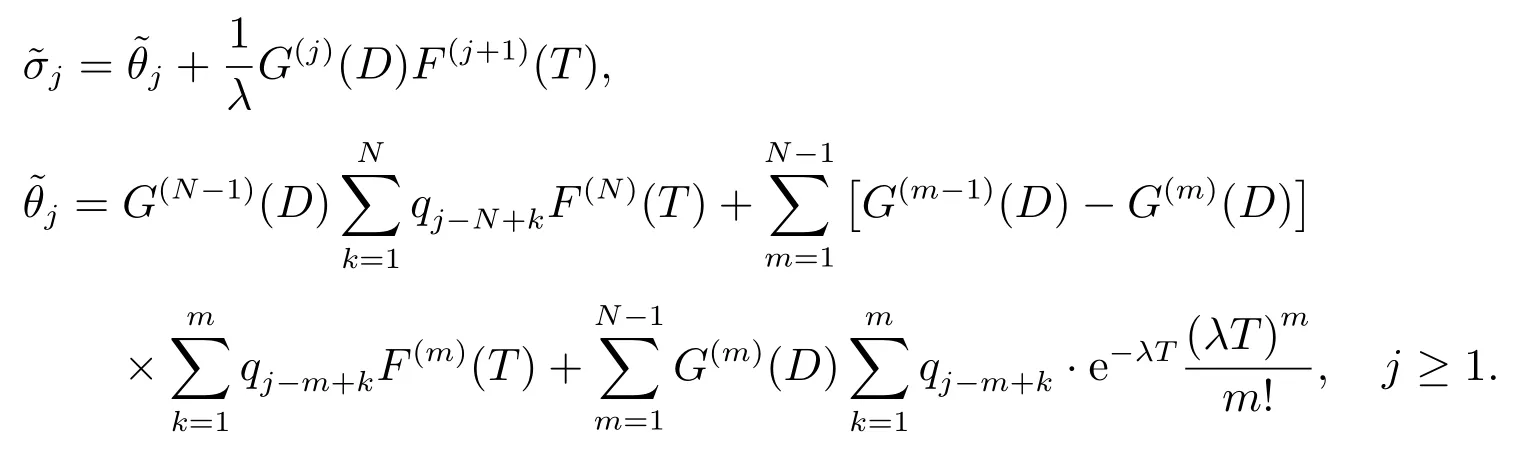
推论2当N →∞时，本文研究的排队系统是在D-策略控制下服务员单重休假且休假可中断的M/G/1 排队系统.对ρ ＜1 时，有

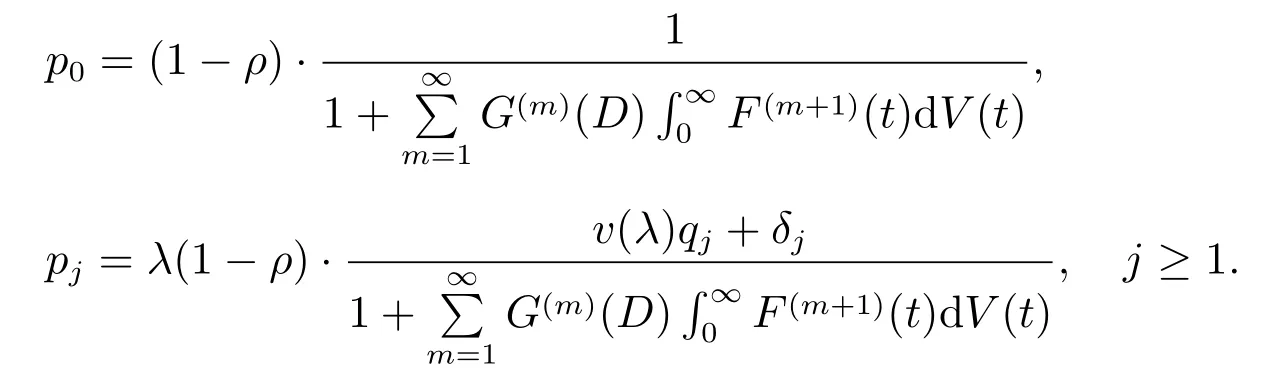
母函数为

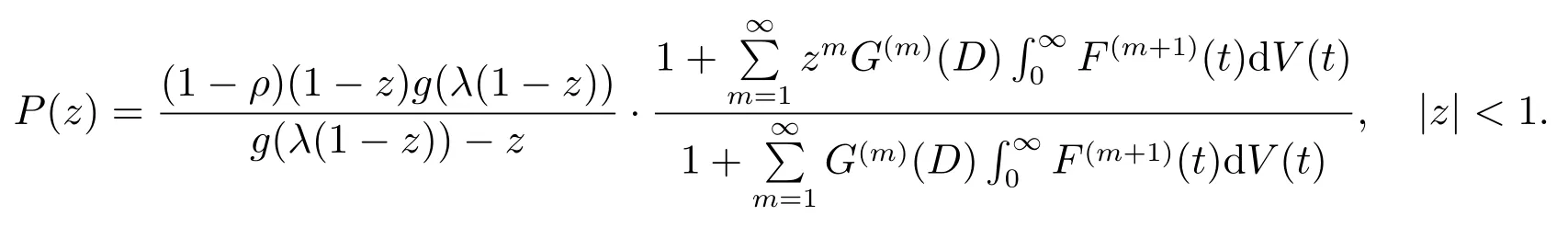
平均队长为

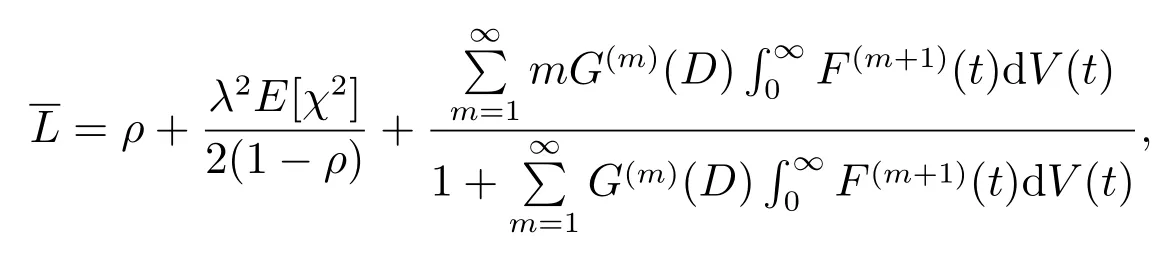
其中

推论3当N →∞,P{V=T}=1 时，本文研究的排队系统是在D-策略控制下服务员具有固定单重休假时间T且休假可中断的M/G/1 排队系统.对ρ ＜1 时，有

母函数为

平均队长为

其中

推论4当D →∞时，本文研究的排队系统是在N-策略控制下服务员单重休假且休假可中断的M/G/1 排队系统，即等价于文献[14]研究的基于单重休假的Min(N,V)-策略控制的M/G/1 排队系统.在上面所得的结果中，令D →∞即可得与文献[14]完全一致的相应结果.

推论5当D →∞,P{V=T}=1 时，即系统是基于固定单重休假时间T的Min(N,T)-策略控制的M/G/1 排队系统，对ρ ＜1 时，有

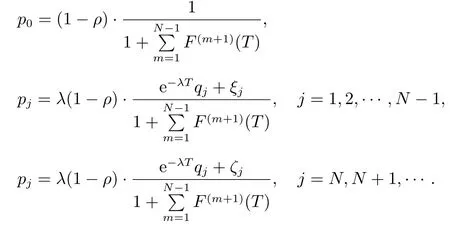
母函数为

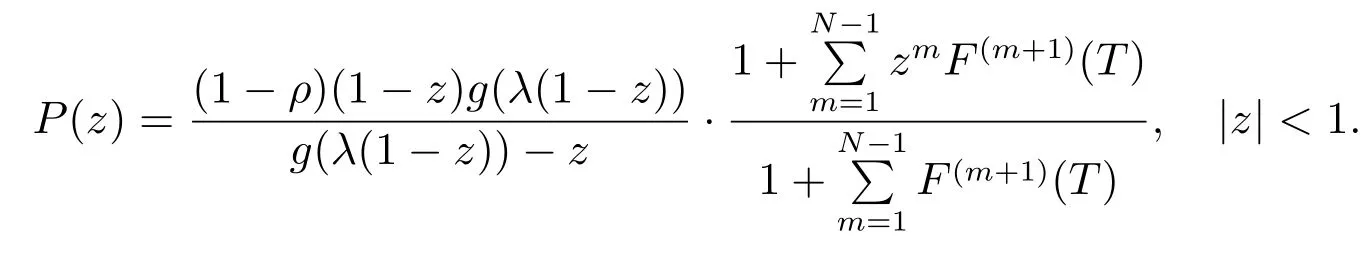
平均队长为

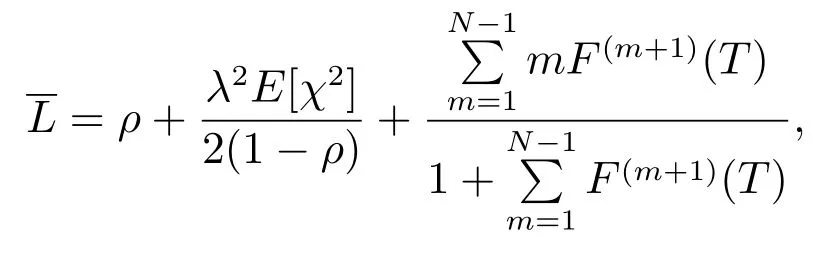
其中

推论6当P{V= 0} = 1 或D= 0 时，本文研究的排队系统等价于文献[23]研究的经典M/G/1 排队系统.在上面所得的结果中，令P{V= 0} = 1 或D= 0 即可得到与文献[23]完全一致的相应结果.

推论7当P{V=∞} = 1 时，本文研究的排队系统等价于文献[15]研究的Min(N,D)-控制策略的M/G/1 排队系统.在上面所得的结果中，令P{V=∞}=1 即可得到与文献[15]完全一致的相应结果.

6 附加平均队长对系统参数的敏感性分析

在本节中，我们通过数值计算实例来分析系统的附加平均队长E[Ld]随着一些参数的变化而变化的情况.由定理5 可知附加平均队长E[Ld]为

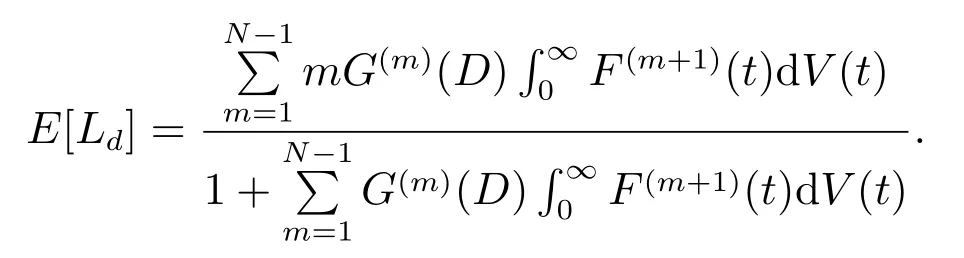
例1当服务时间服从参数µ(＞0)的负指数分布G(t) = 1-e-µt与休假时间服从参数θ(＞0)的负指数分布V(t)=1-e-θt时，代入上述表达式得到附加平均队长E[Ld]为

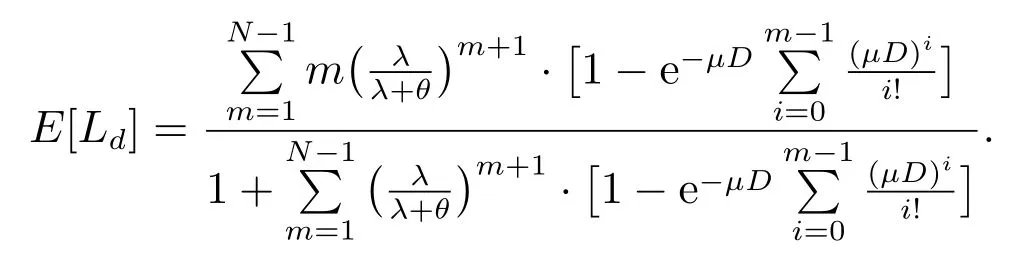
取λ=0.5,ρ=0.75,D=10，然后运用Matlab 软件编程进行计算得到E[Ld]随N与θ的变化情况，见表1 与图1，小数点后保留四位.

取λ=0.5,ρ=0.75,θ=0.25，然后运用Matlab 软件编程进行计算得到E[Ld]随N与D的变化情况，见表2 与图2，小数点后保留四位.

表1: λ =0.5, ρ =0.75, D =10，E[Ld]随N 与θ 的变化情况

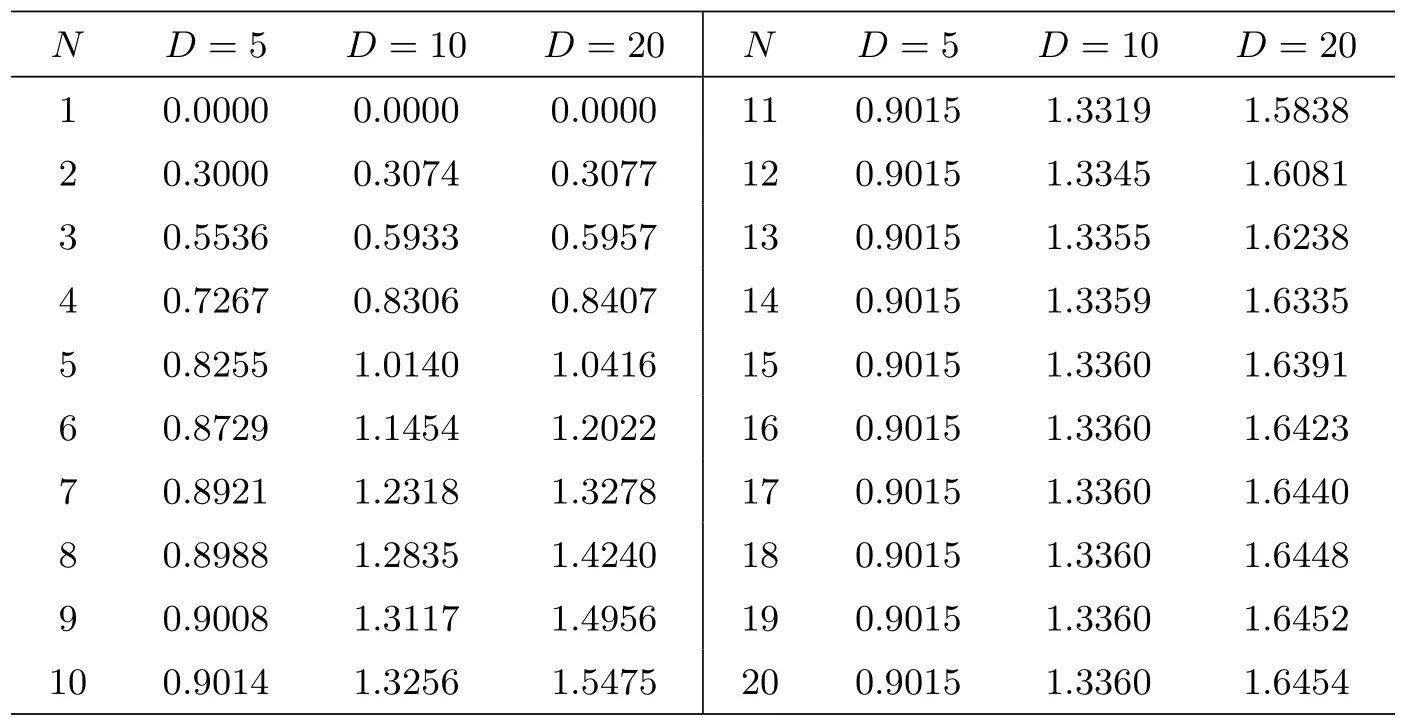
表2: λ =0.5, ρ =0.75, θ =0.25，E[Ld]随N 与D 的变化情况

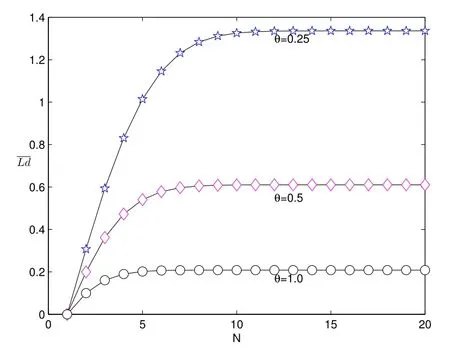
图1: E[Ld]随N 与θ 的变化情况

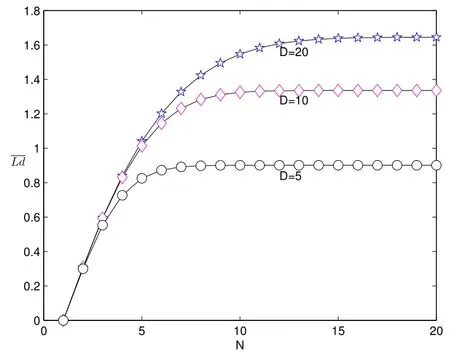
图2: E[Ld]随N 与D 的变化情况

取λ=0.5,ρ=0.75,N=4，然后运用Matlab 软件编程进行计算得到E[Ld]随D与θ的变化情况，见表3 与图3，小数点后保留四位.

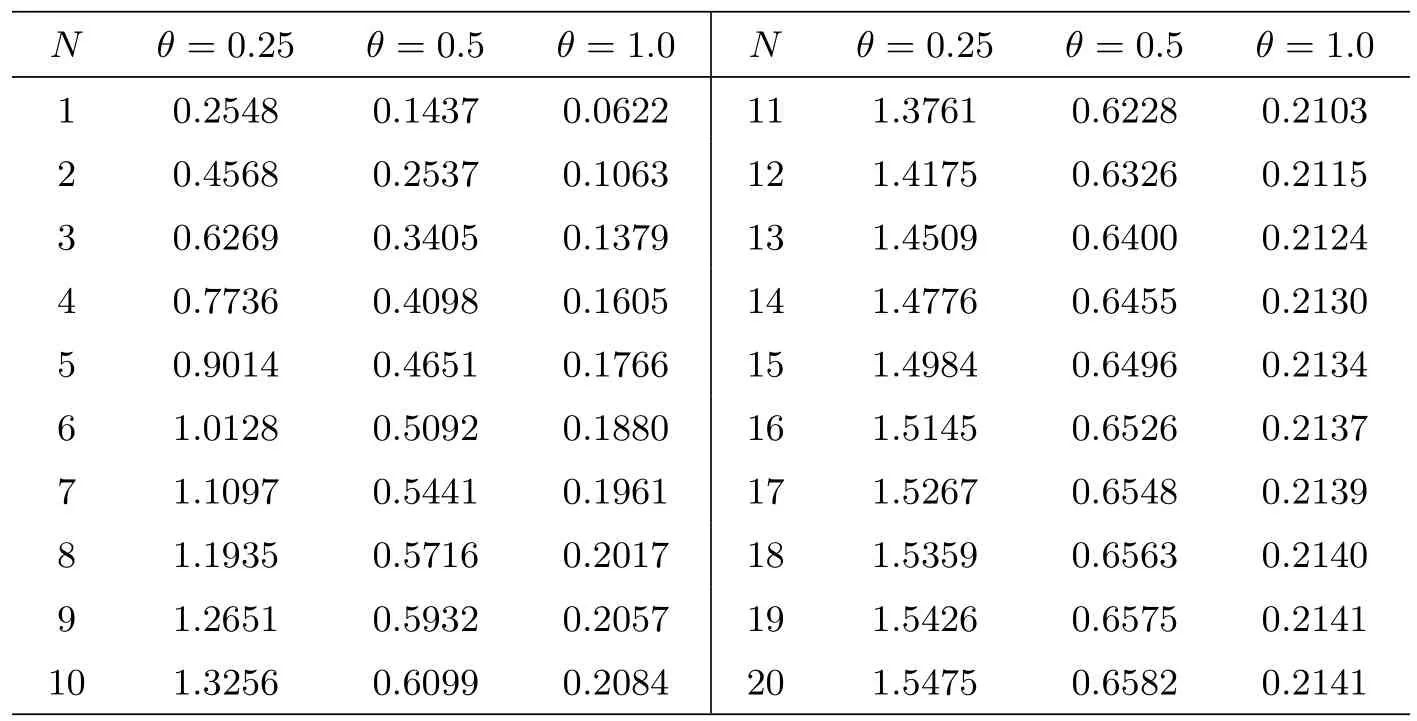
表3: λ =0.5, ρ =0.75, N =4，E[Ld]随D 与θ 的变化情况

图3: E[Ld]随 D 与 θ 的变化情况

例2当服务时间服从参数µ(＞0)的负指数分布G(t) = 1-e-µt与P{V=T} = 1时，即服务员事先约定的休假时间是一个固定时间长度T(＞0)，代入上述表达式得到附加平均队长E[Ld]为

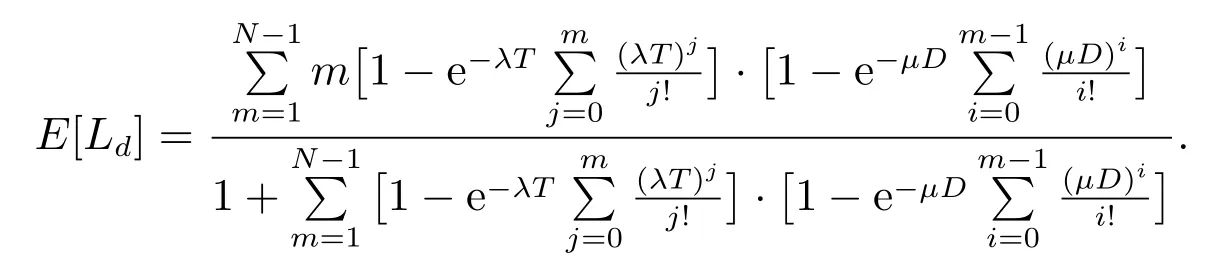
取λ=0.5,ρ=0.75,D=10，然后运用Matlab 软件编程进行计算得到E[Ld]随N与T的变化情况，见表4 与图4，小数点后保留四位.

表4: λ=0.5, ρ=0.75, D =10，E[Ld]随N 与T 的变化情况

图4: E[Ld]随N 与T 的变化情况

从图1 和图4 可以看出，取定参数λ= 0.5,ρ= 0.75,D= 10，当休假时间的参数确定或者休假时间是一个固定时间长度T(＞0)，随着N取值的不断增大，系统的附加平均队长E[Ld]都是先增大而后趋于平稳保持不变，这是因为在N取值增大时，受Min(N,V)-控制策略的影响，N所起的作用越来越小，当N超过某一值时，系统的附加平均队长几乎由服务员的休假决定.且当服务员的休假时间越来越短时，这使得到达系统的顾客有较大机会被服务，因此系统的附加平均队长E[Ld]呈现减小的趋势.

取λ=0.5,ρ=0.75,T=10，然后运用Matlab 软件编程进行计算，得到E[Ld]随N与D的变化情况，见表5 与图5，小数点后保留四位.

从图2 和图5 可以看出，取定参数λ= 0.5,ρ= 0.75，当D(＞0)确定时，随着N取值的不断增大，系统的附加平均队长E[Ld]都是先增大而后趋于平稳保持不变，这是因为在N取值不断增大时，受Min(N,D)-控制策略的影响，N所起的作用越来越小，当N超过某一值时，系统的附加平均队长E[Ld]几乎由参数D决定.同理，随着D取值增大，受Min(N,D)-控制策略的影响，D所起的作用越来越小，系统几乎由参数N决定.

图5: T =10，E[Ld]随N 与D 的变化情况

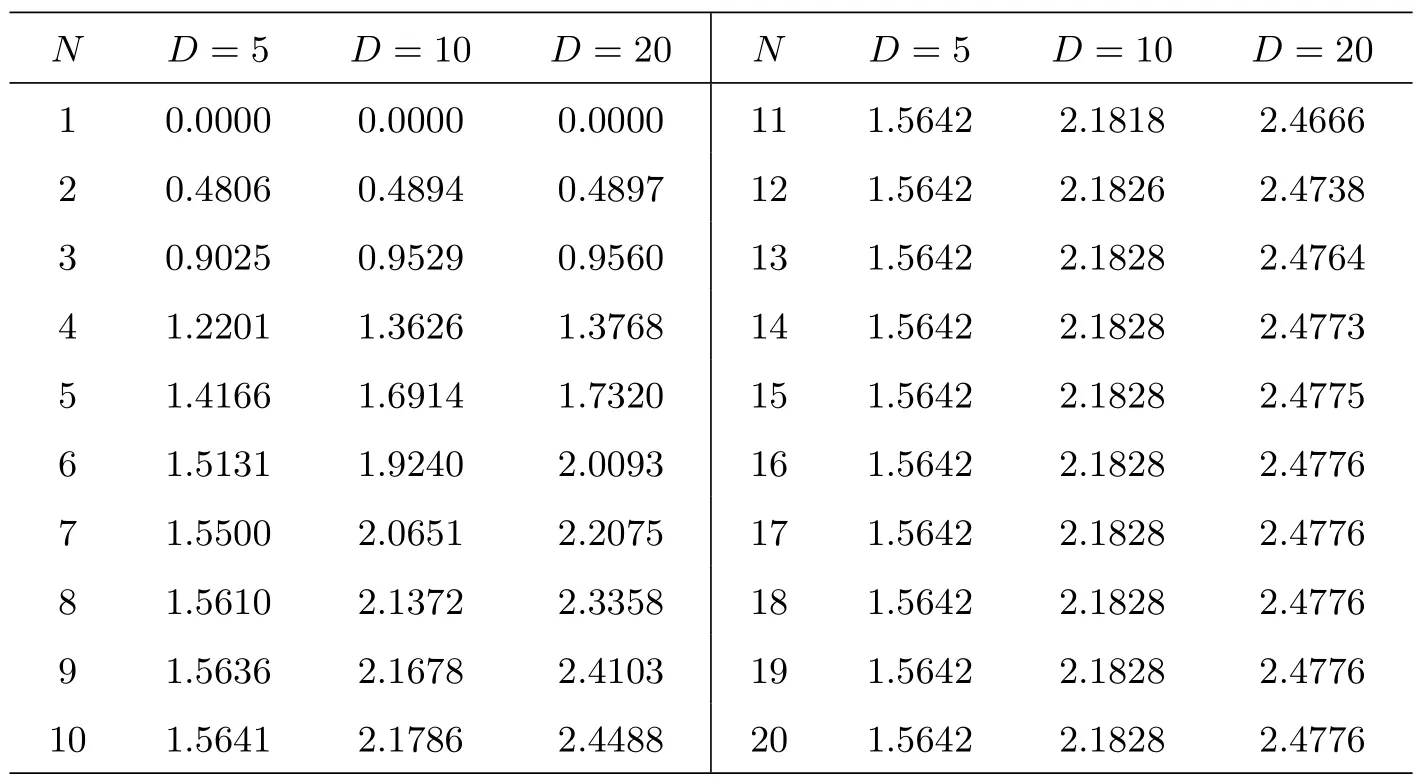
表5: λ =0.5, ρ=0.75, T =10，E[Ld]随N 与D 的变化情况

取λ= 0.5,ρ= 0.75,N= 4，然后运用Matlab 软件编程进行计算得到E[Ld]随D与T的变化情况，见表6 与图6，小数点后保留四位.

从图3 和图6 可以看出，取定参数λ= 0.5,ρ= 0.75,N= 4，当休假时间的参数确定或者取定休假时间是一个固定时间长度T(＞0)，随着D取值的不断增大，系统的附加平均队长E[Ld]都是先增大而后趋于平稳保持不变，这是因为在D取值增大且超过某一值时，D所起的作用越来越小，系统的附加平均队长几乎由休假时间决定.

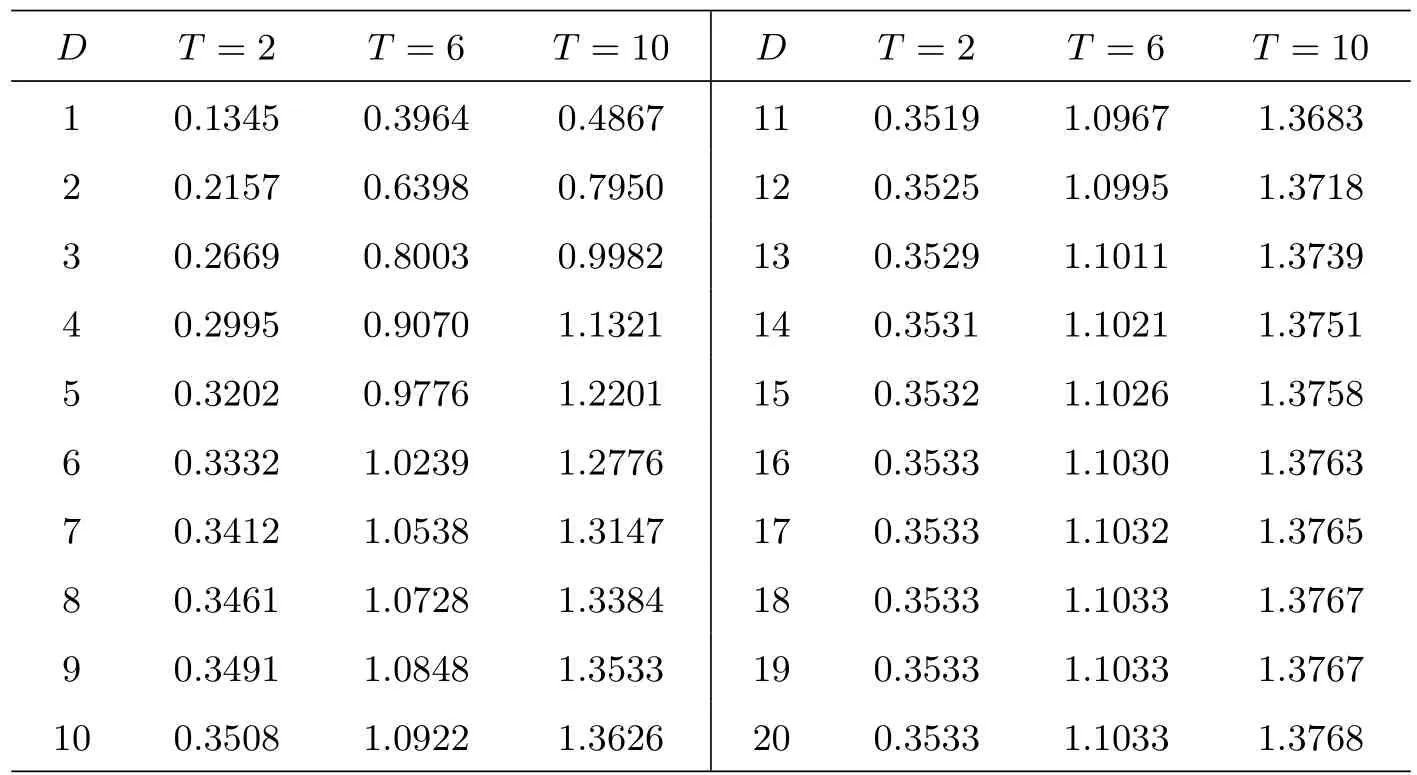
表6: λ =0.5, ρ=0.75, N =4，E[Ld]随D 与T 的变化情况

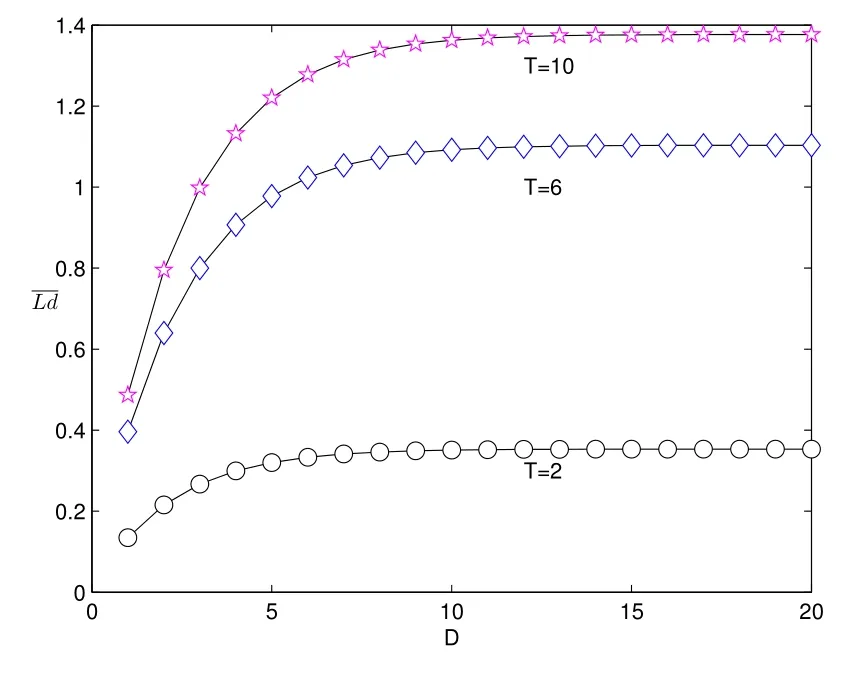
图6: E[Ld]随D 与T 的变化情况

7 结束语

本文讨论了服务员采取单重休假机制和系统采取Min(N,D,V)-控制策略的M/G/1 排队系统，分析了系统队长的瞬态分布和稳态分布，得到了稳态队长的随机分解结构和附加队长分布的显示表达式，进一步给出了一些特殊情形下的相关结果.另外，通过数值计算实例讨论了系统基于单重休假和Min(N,D,V)-策略机制而引起的附加平均队长E[Ld]随着N,D和休假时间V的变化情况，使得本文的研究有更好的应用价值.