Link Prediction in Complex Networks Incorporating the Degree and Community Information

DENG Ya-jing, ZHANG Hai,2,, GUO Xiao, GOU Ming, WANG Yao

(1- School of Mathematics, Northwest University, Xi’an 710127;2- Faculty of Information Technology, Macau University of Science and Technology, Macau 999078;3- School of Mathematics and Statistics, Xi’an Jiaotong University, Xi’an 710049)

Abstract: Recently the structural features of networks are widely used to the link prediction problem.Based on the information-theoretic model, we propose a more general information-theoretic model by encoding various network structural information.Specifically, for the scale-free networks, a set of Neighbor Set Information (NSI)based indices by suppressing the contribution of high-degree neighbors are proposed.Secondly, to incorporate the community information, this paper further presents a set of NSI based indices in which the prior probability of a node pair being connected is encodes the community information of networks.The experimental results on a series of real networks show that our methods outperform other classical link prediction indices.

Keywords: link prediction; scale-free; network community; information entropy

1 Introduction

Link prediction attempts to estimate the likelihood of the existence of a link and predict the generation or trend of the network based on the observed network structure and other available information[1-3].Typically,it consists of the predictions of two kinds of links, namely, missing links and future links.In the past decades, link prediction has attracted a large amount of interest and it has found applications in diverse fields,for example, it can carry out online social recommendation[4], guide protein-protein interaction experiment[5], and identify important links in transportation network[6],among many others.

Over the past decades,various link prediction methods have been proposed[1,2,6-15],they can be coarsely sorted to the following four types: node-based methods,structurebased methods, social-theory-based methods and learning-based methods.According to the characteristics of these methods, structure-based methods can be divided into neighbor-based methods, path-based methods, and random-walk-based methods,social-theory-based methods are also divided into community-based methods and structural hole-based methods,and learning-based methods are further divided into featurebased classification and probabilistic model.

Among these link prediction methods,the most common method is structure-based method.Network structural features describe the basic properties of the networks,which includes common neighbors, links across two neighbor sets, community structure, etc.The simplest framework of link prediction is similarity based, including neighbor-based methods, say common neighbors (CN)[7], Adamic-Adar (AA)[9], and resource allocation (RA)[6], and path-based methods, say, local path (LP)[10], Katz[11],resource allocation along local path (RALP)[12].On the other hand, there exists a certain proportion of methods proposed in the framework of maximum likelihood estimation.Clausetet al[16]developed a hierarchical structure model that estimates the connection likelihood of nodes.Guimer`a and Salespardo[17]presented a stochastic block model to estimate the probability that two nodes are connected.Liuet al[18]proposed a fast blocking probability model based on a greedy algorithm, which not only reduces the computation complexity but also improves the prediction accuracy.Based on information theory[19,20],Tanet al[21]designed a mutual information method,where they employed the information value of the common neighbors to measure the connection likelihood of a node pair, which can greatly improve the prediction accuracy.Most of the aforementioned methods focus on just one kind of network structural features which may lose other available information.Therefore it is an important problem to integrate the strengths and benefits of different methods in an attempt to improve the prediction accuracy.Zhu and Xia[22]proposed an information-theoretic model,where the information values brought by various network structural features are modeled as additive.In more details, two types of local structural features,namely,the common neighbors and the links across two neighbor sets, were employed to generate the presented neighbor set information (NSI) index.

On the other hand, many real networks are scale-free, i.e., the degree distribution follows a power law[23].The most notable characteristic in a scale-free network is the existence of vertices known as ‘hubs’, whose degree exceed the average greatly.The contributions of hub nodes and ordinary nodes to their neighbors are different, previous studies have shown that suppressing the contribution of the high-degree common neighbors can improve the performance of link prediction.Additionally, real networks have communities[24], that is, the network consists of a number of communities, and links between the nodes within the same community are relatively dense whereas links between the nodes from distinct communities are relatively sparse.Therefore the community of nodes should be considered when calculating the probability of a node pair being connected.However, the NSI index does not incorporate the scale-free property and the community structure of real networks.

In this paper, we study the link prediction problem by integrating the strengths and benefits of different methods while incorporating the degree and community information.We treat the NSI index as the baseline method which combines the strength of two network structural features, namely, common neighbors and links across two neighbor sets.To incorporate the degree information, we adjust the weights of the two network structural features in the NSI index by applying AA, RA, and RALP indices,which aims to suppress the contribution of high-degree neighbors.Moreover,to encode the community information, the prior probability of two nodes being connected is calculated according to the communities they belonging to.Finally, we conduct a series of real networks experiments to show the superiority of our methods.

2 An information-theoretic model for link prediction

In this section,we first briefly review the general information-theoretic framework[22]which uses the information of a variety of network structural features.Then a typical information-theoretic method based on common neighbors and the links across two neighbor sets[22]is presented.

Given an undirected networkG(V,E), whereVandEare the sets of nodes and links, respectively.LetUdenote the universal set of all possible links.ThenU-Eis the set of nonexistent/missing links.The goal of link prediction is to find out the missing links from the setU-E.We first consider the case where just one feature is available, and give some notions and notations.Given a feature associated with the candidate node pair (x,y), and the set of feature variables is denoted by Ω, whose element is denoted byω,the event of the disconnected node pair(x,y)being connected is denoted as.Then the link prediction problem can be regarded as estimating the uncertainty of eventwith the information contained in Ω.On the basis of the information theory[19,20], the likelihood of a link between a node pair can be estimated by conditional self-information denoted asI(|Ω).Giving the above definitions,Zhu and Xia[22]defined the likelihood score of a disconnected node pair as

To combine the information brought by various features, Zhu and Xia[22]extended the above formulation to incorporate various features as follows

whereλireckons the contribution of featureito the finial connection likelihood.

The preceding paragraphs introduced the general information-theoretic framework,and we now give a special case presented in Zhu and Xia[22],which used the information of neighbor set.Consider a networkG(V,E), whereVandEare the node set and link set, respectively.Let Γ(x) denote the neighbor set of nodex, and letkxdenote the degree of nodex.Specifically, the common neighbors of a node pair (x,y), defined asOxy={z:z ∈Γ(x)∩Γ(y)}, and the links across neighbor sets Γ(x) and Γ(y), defined asPxy={lst:lst ∈E,s ∈Γ(x),t ∈Γ(y)}, are employed.Formally, the link likelihood of a node pair is defined as

Based on (1), the likelihood score can be rewritten as

where

is the prior probability of the connection of a node pair (x,y) and it indicates the link density in the training set.is the clustering coefficient of nodez, denoted as

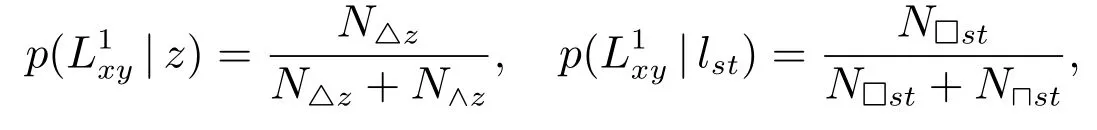
whereN△zandN∧zstands for the number of connected and disconnected node pairs whose common neighbors isz, respectively,N□ststands for the number of connected node pairs whose neighbors aresandt, respectively andN⊓stdenotes the number of disconnected node pairs whose neighbors aresandt, respectively.

The index is called the neighbor set information (NSI) index.Note that, in (3),eachzinOxyand eachlstinPxyis equally important as (3) simply takes the unweighted summation over the set.It is obvious that thewhich measures the sparsity of the network, are identical for different node pairs.However, as mentioned in the preceding paragraphs, nodes with distinct degrees play different roles in the link prediction procedure, and the prior link probability of a node pair is associated with the communities they belong to.Therefore, it is natural to incorporate the degree and community information into the NSI index in an attempt to improve the link prediction accuracy.

3 NSI indices based on scale-free property

In this section, we propose some new indices which incorporate the scale-free information into NSI.Then we conduct a series of real network experiments to evaluate the performance of our proposed indices.

3.1 NSI indices based on scale-free property

Many real networks are scale-free, so the degree is not uniformly distributed.Literatures have shown that the link prediction accuracy can be improved by suppressing the contributions of the high-degree common neighbors of disconnected node pairs[2,6].Therefore, we here take the degree information of nodes into account to improve link prediction performance.To this end, we modify the NSI index by introducing weights into the summations according to the degree.We give two weight functions,f(kz)andf(ks,kt), which characterize the contributions of nodes and links according to the degree information, respectively.Then the general form of NSI indices based on the degree of nodes (DNSI) is formulated as follows

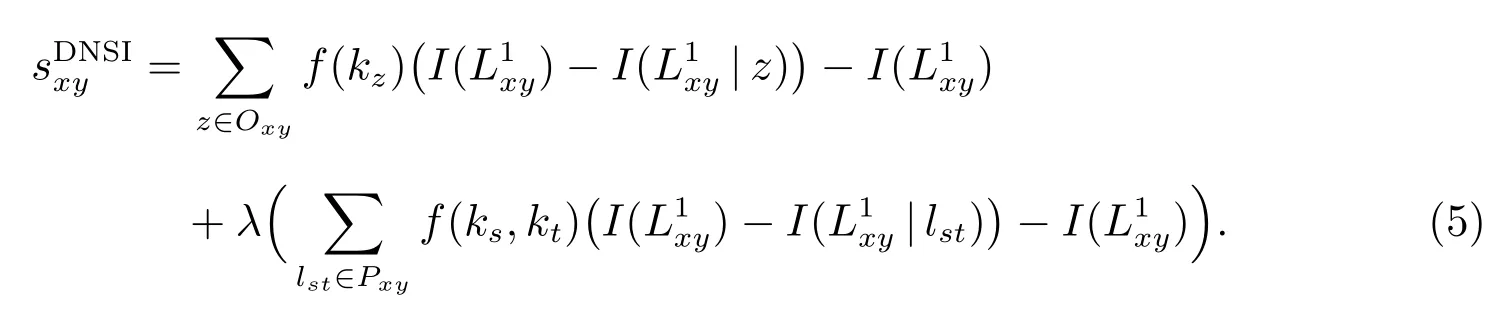
Next we provide several typical examples of the general form (5).Among the similarity based link prediction indices,AA,RA and RALP indices penalize high-degree neighbors in different ways based on CN and LP indices.We employ the spirit of these indices and propose the following three indices, NSI-AA, NSI-RA, and NSI-RALP

whereλis a tuning parameter controlling the weights of the two features.

3.2 Experimental analysis

In this subsection, we conduct a series of real network experiments to test the performance of the proposed methods.First, we introduce some datasets we used and then the experimental results are provided.

3.2.1 Data sets

We consider 12 typical real networks from various fields in our experiments,including the adjective adjacencies network(Adjnoun), the foodweb network 1 (Baydry), the foodweb network 2 (Baywet), the foodweb network 3 (Foodweb), the co-occurances of characters network (Lesmis), the network of US air transportation (USAir), the neural network of the nematode worm C.elegans (C.elegans), the friendship network of a karate club (Karate), the American college footall network (Football), the network of interpersonal contacts between windsurfers (Beach), the network of the US political blogs (PB) and the protein-protein interaction network (Yeast), where we use the abbreviations in the parenthesis to represent them in this section.These datasets can be downloaded from Koblenz Network Collection (KONECT[25]).

The 12 networks are all regarded as undirected and unweighted networks in the following paragraphs.We summarize the basic structural features of the 12 networks in Table 1.The detailed topological features of the networks are presented as follows,nandmdenote the number of nodes and links in the network, respectively.ddenotes the link density, which is defined as the ratio of the number of existing links to that of all possible links.The average degree and the average shortest distance are denoted bykandl, respectively.Candrrepresent the clustering coefficient and assortative coefficient, respectively.The clustering coefficient is the number of closed triplets over the total number of triplets (both open and closed), and it measures the degree to which nodes in a network tend to cluster together.The assortative coefficient can be measured by the Pearson correlation between the degree of the connected nodes.Hdenotes the relative edge distribution entropy, which measures the equality of the degree distribution.

Table 1: The basic structural features of twelve real-world networks

3.2.2 Experimental results

We compared several typical indices, including the proposed indices, namely, NSIAA,NSI-RA,NSI-RALP and the benchmark index NSI,among others.Area under the receiver operating characteristic curve(AUC)[26]was employed to evaluate the accuracy of each link prediction procedure, where a larger AUC indicates better performance.We randomly divided the existing links to two parts, that is, 90 percent as the training set and 10 percent as the test set.We repeated the divisions 10 times and calculated the average AUC on the test set over 10 replications.Note that the NSI based methods depend on a tuning parameterλ, hence the AUC is actually a function ofλ, and it varies withλ.

Figure 1 shows the AUC of 12 different networks with respect to several indices asλvaries from 10-4to 104.For the ease of presentation, we only showed the results with respect to four NSI based indices.As expected, the performance of each method varies with the tuning parameterλ.However, we find that NSI-AA, NSI-RA, and NSI-RALP perform better than NSI in the sense that the highest AUC among all are never produced by NSI.Indeed, NSI-RALP always achieves the highest possible AUC.Moreover, whenλ= 0.1, the NSI, NSI-AA and NSI-RA always produce satisfactory performance with respect to the 12 real world networks, whereas for the NSI-RALP,λ=10 is a reasonable choice.

Figure 1: AUC results of the NSI and DNSI indices in twelve networks

Table 2 presents the optimal AUC of typical methods, that is, theλis selected from 10-4to 104to be the maximum point of the AUC (the best performance is emphasized by bold font).The results show that NSI based methods outperform other typical methods for almost all 12 networks,which demonstrates the merits of combining different features in the information-theoretic model.In particular, our DNSI indices achieve good prediction accuracy as they take the degree information into consideration.Among the three DNSI indices, NSI-RALP performs best, which is because the NSIRALP index suppresses not only the contribution of the high-degree common neighbors,but also that of the all high-degree neighbors.

Table 2: Comparison of the AUC metric of the NSI and DNSI indices with a optimal parameter in twelve networks

It is generally time demanding to search for the optimalλ.Therefore, it is pivotal to give a referenceλfor each method.As we have mentioned, the NSI, NSI-AA, and NSI-RA with, and the NSI-RALP withλ= 0.1 always yield good performance.We list their performance in Table 3.It can be seen that the prediction performance of each index with a fixedλis consistent with that with the optimalλ.Hence, in the subsequent applications, one can directly setλto a fixed value, rather than searching for its optimal value, which improves the efficiency of the algorithm to a large extent.

4 NSI indices based on community structure

In this section, we propose some new indices which further encode the community information besides the degree information into the information-theoretic model.Then we use real network experiments to illustrate the superiority of the proposed methods.

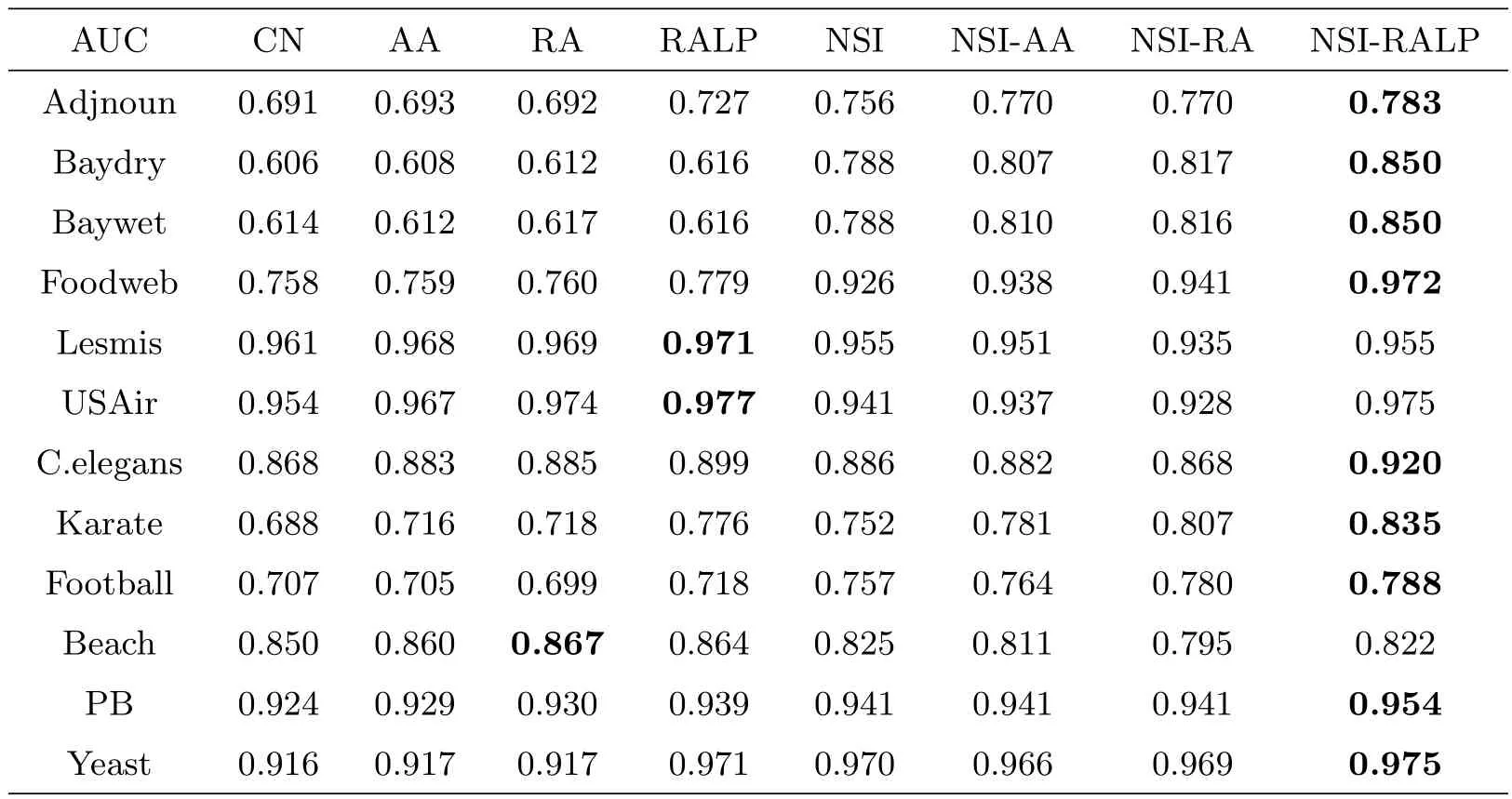
Table 3: Comparison of the AUC metric of the NSI and DNSI indices with a fixed parameter in twelve networks

4.1 NSI indices based on community structure

Note that in (4), the prior probability of every two disconnected node pair is the number of the existing links over the number of all possible links.However, many real networks have community structure, and the links within the same community are expected to be denser than that across different communities.Therefore,it is natural to think that the prediction accuracy can be improved by incorporating the community information into the NSI index.In what follows, we propose the NSI based indices encoding the community information (CNSI).

We use the inner link density and connecting link density as the prior probabilityof the connection of a disconnected node pair (x,y).For a communityµwith|Vµ|number of nodes and|Eµ|number of links，the inner link density of the community is the ratio of the number of inner links to the maximum possible number of links in the communityµ, denoted by

Now we turn to give the definitions for the connecting link density between every two distinct communitiesµandν.Suppose|Eµν| is the number of links between two communities, and|Vµ| and|Vν| are the number of nodes in the two communities,respectively.Hence the product of|Vµ| and|Vν|denotes the maximum number of links that can exist between the two communities, and the connecting link density is defined as

Next, we propose a new model which incorporate the community structure feature of the network.We modify the prior probability of two disconnected node pair in the NSI index with the community information.Precisely, if the nodesxandybelong to a common communityµ, thenOtherwise, if nodexandybelong to two distinct communityµandν, respectively, thenThe CNSI and CDNSI indices are formulated as follows

4.2 Experimental analysis

Similar to the treatment in section 3, we compared the performance of all the NSI based methods, including the DNSI indices, the CNSI indices and the benchmark NSI index.Specifically, for the CNSI methods, we firstly use Newman’s fast community detection algorithm[27]to detect the community, then we applied the CNSI procedure to predict links.The fast community detection algorithm is effective and the different community detection algorithms have little effect on the results of the link prediction.We plotted the AUC of CNSI and CNSI indices based on degree (CDNSI) as functions of the ratioλin Figure 2.According to Figure 2, for the NSI-RALP and CNSI-RALP,we chose the tuning parameter to beλ= 10, and for the remaining indices,λwere fixed as 0.1.The average AUC with respect to each index are summarized in Table 4.As expected, the indices which further incorporate the community information show better prediction accuracy than those which only incorporate the degree information.Thus showing the merits of our proposed method.In particular,the CNSI-RALP index performs the best for almost all networks but the Football and Beach networks, hence we recommend using the CNSI-RALP index in subsequent applications.

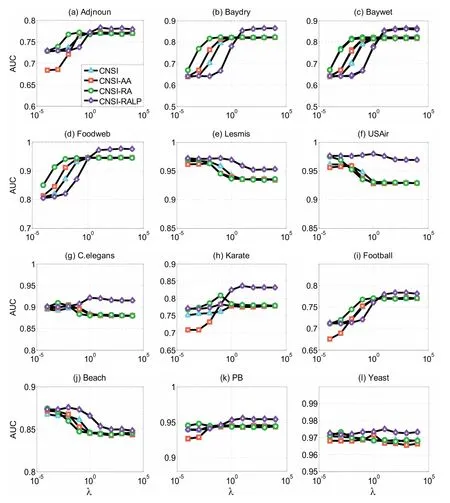
Figure 2: AUC results of the CNSI and CDNSI indices in the twelve networks

5 Conclusions

In this paper,we have proposed a class of link prediction indices by integrating the benefits and strengths of different methods while encoding the degree and community information of the networks, where degree and community structure are encoded to further enhance the distinguishable extent of candidate links.Based on the NSI index which combines the strength of two network structural features,namely,common neighbors and links across two neighbor sets,we have proposed a class of indices by adjusting the weights of the two network structural features in the NSI index to incorporate the degree information.Furthermore,we have developed the second class indices to encode the community information by formulating the prior probability of two nodes being connected according to the communities they belong to.In summary, our methods can take advantage of various available features to make a better prediction, and it can differentiate the contributions of different structural features.

Table 4: Comparison of the AUC metric of the NSI based and CNSI based indices with fixed parameter in the twelve networks

Through experiments on a series of real networks,we find that NSI index encoding the degree information has higher prediction ability measured by AUC than NSI and other typical similarity indices.The results also indicate that incorporating both the degree and community information into the NSI index can yield highest prediction accuracy among all the typical link prediction indices.In particular, our proposed CNSI-RALP index performs the best compared to the state of the art methods.

Our methods can be used for solving various link prediction problems and improving prediction performance,especially for scale-free networks and community structured networks.We have mainly focused on undirected and unweighted networks in this paper, whereas weighted or directed networks also arise in the real world.So it would be interesting to generalize the presented work to those cases.