分数阶具有不确定项和外扰的超混沌金融系统的滑模同步

毛北行

(郑州航空工业管理学院数学学院，郑州 450015)

1 引言

混沌同步是基于主从系统或者驱动系统与响应系统实现同步化，而系统误差逐渐趋近于坐标原点时就认为系统取得了同步.分数阶非线性混沌系统的同步已经成为研究的主要课题[1,2]，例如：文献[1]研究具有外扰不确定分数阶Victor-Carmen 系统的滑模同步问题，文献[2]研究了一类分数阶系统的有限时间同步控制.Mohammad 等[3]研究了一类分数阶系统的同步，同步时间在有限时间间隔内完成.徐瑞萍和高明美[4]、李鹏和郑志强[5]、侯瑞茵等[6]利用积分滑模技巧研究一类分数阶系统的同步.滑模控制近年来越来越受到控制界的重视.滑模同步已经取得了很多成果，例如：毛北行等[7]研究了分数阶Victor-Carmen 系统的自适应滑模同步；毛北行[8]研究了纠缠混沌系统的比例积分滑模同步)；毛北行[9]基于新型滑模趋近律方法研究了分数阶Duffling 系统的同步控制；毛北行和程春蕊[10]研究了分数阶Sprott 系统的同步问题，设计了适应律和控制器；毛北行和周长芹[11]研究了分数阶Duffling 系统的终端滑模同步.

另一方面，金融系统的混沌同步问题引起了学者的密切关注，朱涛等[12]研究了时滞金融系统的同步问题，毛北行和张玉霞[13]研究了分数阶金融系统的滑模同步问题，但以上两篇文献研究的都是三维金融模型的混沌，然而分数阶不确定四维金融超混沌系统结构比三维系统更为复杂，而分数阶四维超混沌金融系统的滑模同步方面的研究还不很多见[14]，在以上研究的基础上，本文研究了分数阶具有外扰和不确定项的超混沌金融系统的滑模同步.

2 滑模同步

考虑金融超混沌系统[14]

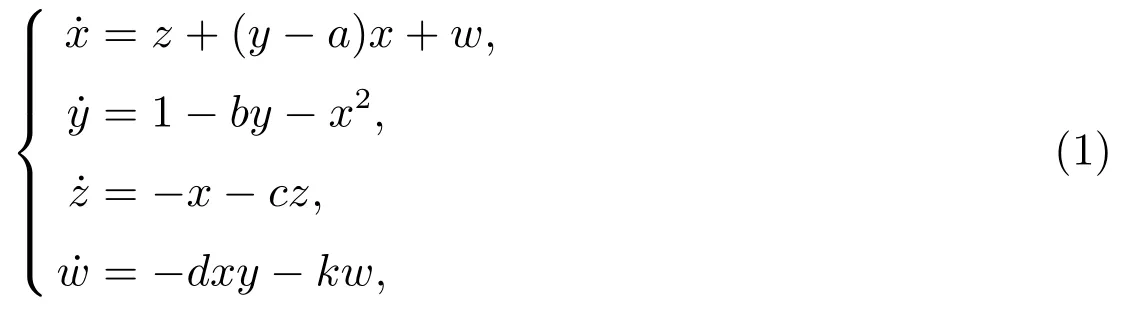
a=0.9,b=0.1,c=1.5,d=0.2,k=0.17 时，系统出现奇怪吸引子，如图1 所示.

图1: 系统吸引子相图

定义1[15]分数阶Caputo 微分定义

将系统(2)设计为主系统

其中 0＜q ≤1 为常数.

设计从系统为

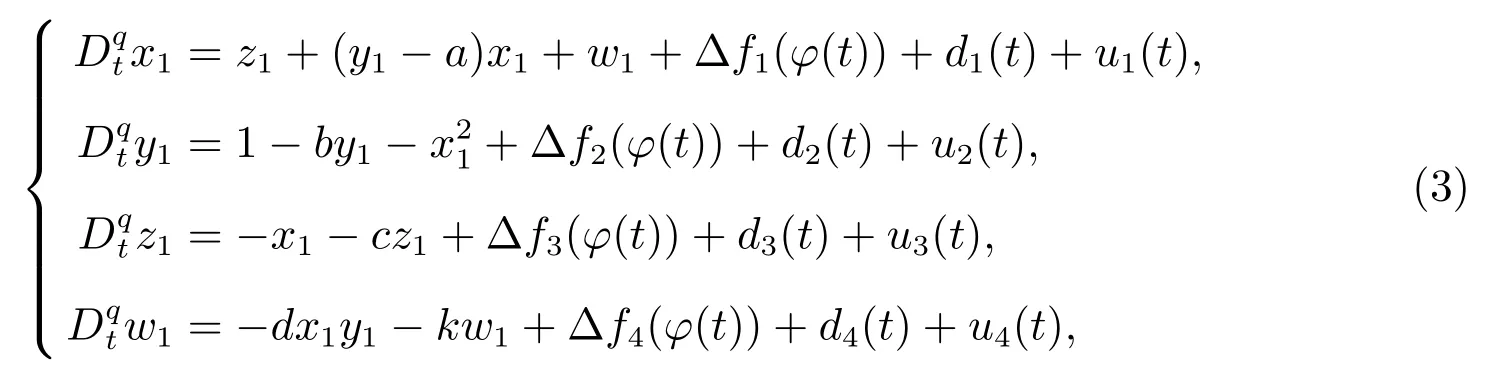
其中φ(t) = [x1,y1,z1,w1]T, ∆fi(φ(t))为不确定项，di(t)为外部扰动.定义误差e1=x1-x,e2=y1-y,e3=z1-z,e4=w1-w，得到

假设1存在未知正常数mi,ni ＞0(i=1,2,3,4)，满足

由于混沌系统轨迹有界，所以假定不确定项和外部扰动为有界变量是合理的.

假设2i=1,2,3,4.

引理1[15]若x(t)为连续可微的函数，则有

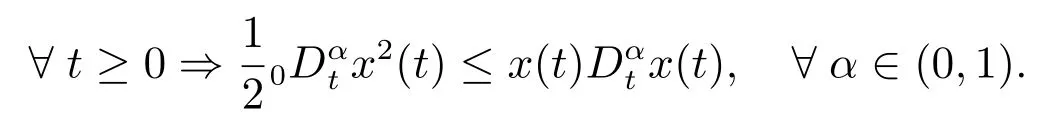
引理2[16]若函数f(t)在[0,+∞)上一致连续，并且广义积分存在，则有

滑模运动分两个阶段：第一阶段即到达段，第二阶段即滑模段.本文设计的滑模运动到达段设计为等速趋近律，滑模函数设计为容易得到如下结论.

定理1在假设1 和假设2 下，构造滑模面控制器

和自适应规则

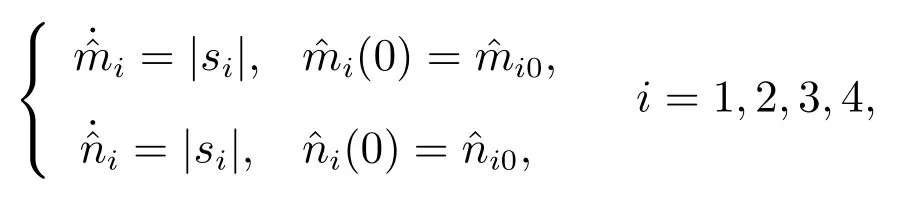
不发生滑模运动时，因为si(t)=Dq-1ei(t)，构造

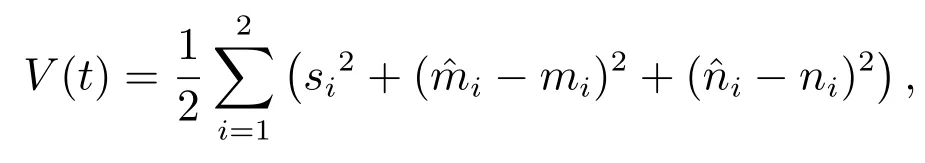
利用假设2，从而

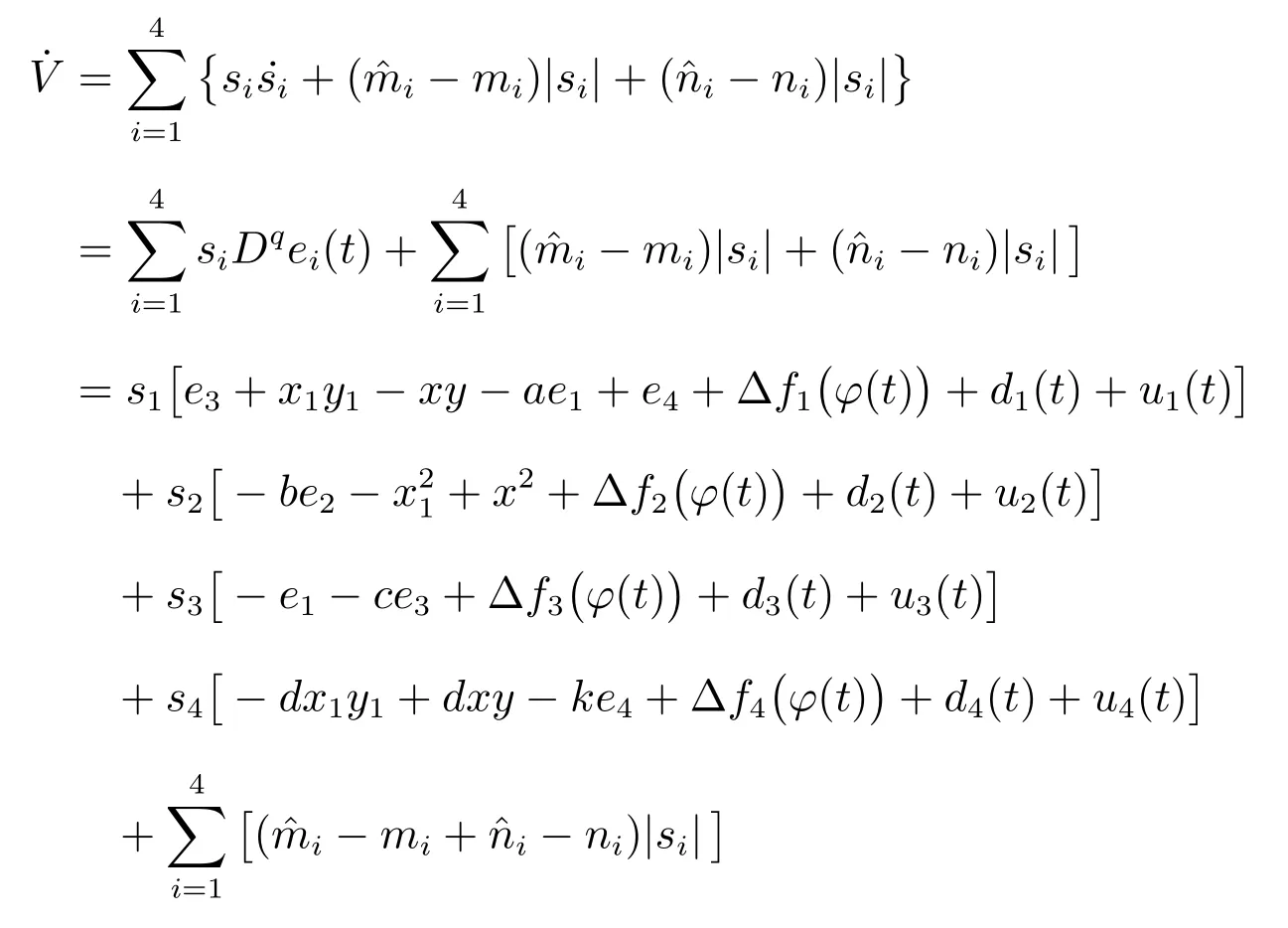
上式两边积分

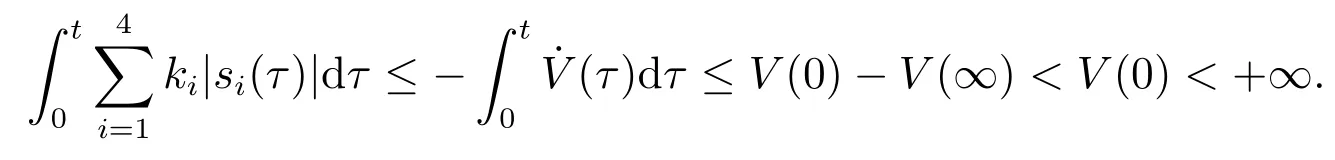
利用引理2，si(t)→0⇒ei(t)→0.

3 积分滑模同步

将系统(2)设计为主系统，设计从系统为

其中φ(t) = [x1,y1,z1,w1]T，∆f(φ(t))为不确定项，d(t)为外部扰动.定义误差e1=x1-x,e2=y1-y,e3=z1-z,e4=w1-w，得到

假设3存在未知参数m,n ＞0，满足|∆f(φ(t))|＜m,|d(t)|＜n.由于轨迹有界，所以可以做上述假设.

假设4|∆f(φ(t))+d(t)-e1|＜λ|e3|.

假设5其中x1+x非零有界，由于混沌系统轨迹有界，可以作此假设.

定理2在假设3 至假设5 条件下，构造滑模面

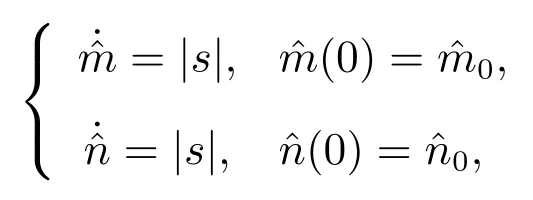
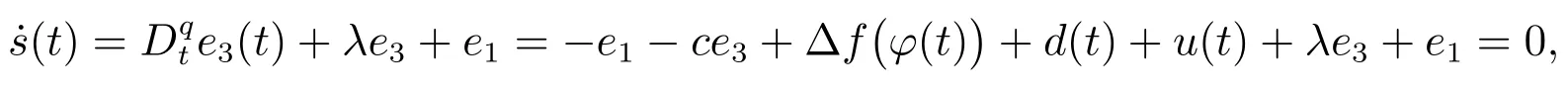
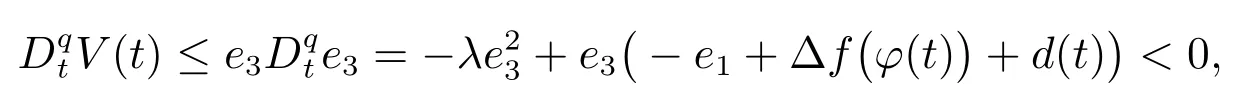
从而e3→0.

因而e2→0.又由于混沌系统轨迹有界，所以-(x1+x)非零有界，

由e2→0，从而根据假设5 得到e1→0.

根据第四方程

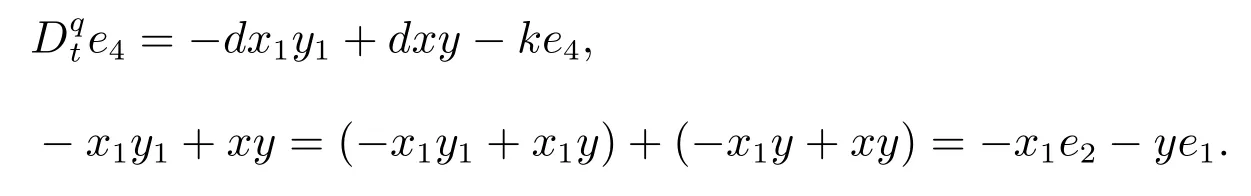
因x1,y有界，e1,e2→0，从而-x1y1+xy →0，所以

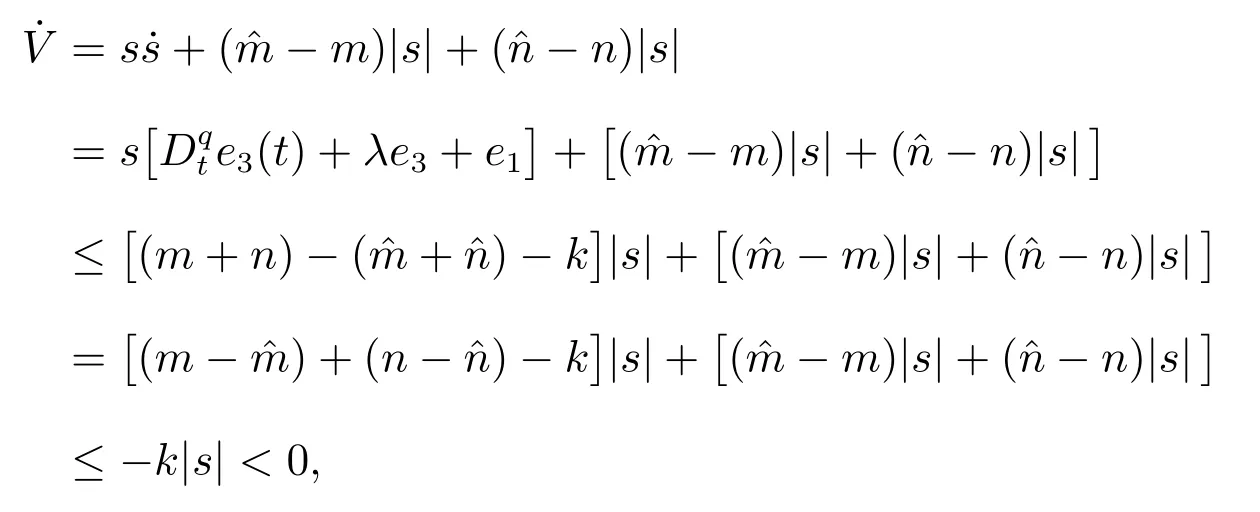
由引理2 得到s →0.

4 数值仿真

系统参数为a= 0.9,b= 0.1,c= 1.5,d= 0.2,k= 0.17,q= 0.92，设置初始值为(x(0),y(0),z(0),w(0)) = (2.2,6.5,2.5,1.5), (x1(0),y1(0),z1(0),w1(0)) =(3,4,3,4.5)，不确定项和外扰取

定理1 和定理2 中系统的误差曲线，如图2 和图3 所示，图中可以看到，初始时刻系统的误差相差较大，随时间的推移误差逐渐趋向一致.定理2 中达到同步需要更少时间，并且金融超混沌系统能够在有限时间趋于同步，定理1 中有四个控制器而定理2 只有一个控制器就能完成，且控制器相对较简单.

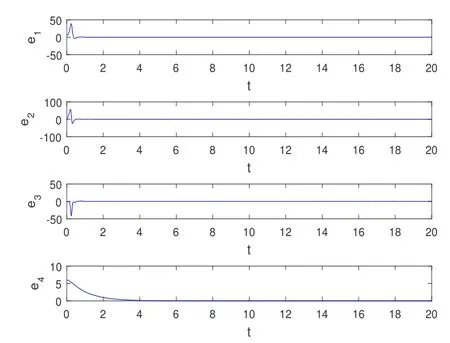
图2: 定理1 中的系统误差

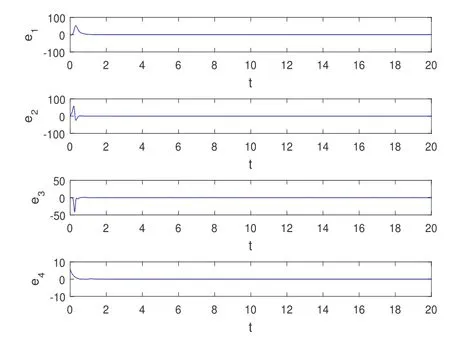
图3: 定理2 中的系统误差

5 结论

研究了分数阶不确定四维金融混沌系统滑模同步的两种方法，设计了分数阶滑模函数和适应规则，得到了分数阶金融超混沌系统的驱动-响应系统取得滑模同步的两个充分性条件，用Matlab 仿真技术验证了所得结论.