考虑通胀风险的个人最优行为投资决策

郭文旌, 蒋海雯

(南京财经大学金融学院，南京 210023)

1 引言

Merton[1]开创性地在连续时间模型下研究了个人最优投资组合选择的问题.之后，许多学者对Merton 经典连续时间模型进行了拓展和研究.但是，传统的投资组合选择理论一般是以期望效用最大化模型(EUM)为基础，即假设投资者是理性的，当他们面对不确定性时是风险厌恶的.然而，在现实生活中，投资者并非是完全理性的.Kahneman 和Tversky[2-4]发现，在许多情况下，投资主体的行为会与经典的投资组合选择理论(Merton, 1969)中的标准路径相偏离.在收益时，投资主体是风险厌恶的，但在遭受损失时，却表现出了风险偏好，并不是传统模型中简单的风险厌恶.同时，相对于收益，投资主体对损失更为敏感，这就是所谓的损失厌恶.为了弥补期望效用最大化模型的这个缺点，Tversky 和Kahneman[4]提出了累积前景理论(CPT).作为累积前景理论的核心，损失厌恶能够解释许多现象，比如：禀赋效应、现状偏见和股权溢价之谜，而这些现象与传统投资组合选择理论却相互矛盾.因此，越来越多的学者把损失厌恶行为特质与最优资产配置问题相结合.Berkelaar 等[5]在考虑损失厌恶的前提下，研究了资产配置问题，在考虑两段式的效用函数时得出了最优策略.Jin 和Zhou[6]建立了损失厌恶特质下的连续时间投资组合选择模型.Zhang 等[7]进一步研究了这个模型，并假设其中的损失是先验的，受限于给定水平，通过解决凹函数Choquet 最小值问题，得到了最优投资策略及最终财富水平.Mi 和Zhang[8]在不完全市场设定下考虑了相同的问题.Guo[9]则将该问题拓展到了保险市场，运用鞅方法求解了损失厌恶的保险公司的最优投资组合选择问题.然而，上述行为投资组合方面的研究都未将通胀风险纳入考量.

通胀风险是投资者面临的基本风险之一，是会引起资产价值和投资收益缩水的风险.Campell 和Viceira[10]发现通货膨胀的存在使得股票投资面临更高的风险.冯蕾和梁治安[11]认为对于中长期投资而言，考虑通胀风险是十分有必要的.因此，国内外许多学者研究了在通胀风险背景下的最优投资组合问题.Fischer[12]研究了家庭资产最优化决策中通胀指数债券的需求，并强调了引入通胀指数债券的必要性.Brennan 和Xia[13]研究了考虑通胀的动态投资组合最优化问题，运用鞅方法求解了幂效用函数下的显式解.丁传明和邹捷中[14]在考虑通货膨胀影响前提下，运用动态规划方法求解了最优消费投资策略问题，并得到了HARA 型效用函数下的显式解.Gong 和Li[15]在通胀风险的情况下研究了投资的最优决策问题.吕会影等[16]在通胀环境下考虑随机微分效用的最优消费投资问题，运用动态规划方法推导出了最优策略.然而，上述文献均假设投资者是风险厌恶的，目前还没有文献考虑到通胀风险对于损失厌恶型投资者在投资组合策略方面的影响.

因此，本文将考虑投资者的损失厌恶行为特质，并引入通胀指数债券来对冲通胀风险，求解考虑通胀风险的个人最优行为投资决策问题.本文的结构如下：第2 节介绍了本文的模型；第3 节详细推导了最优投资策略以及最优的最终财富解析解；第4 节运用数学分析手段，对最优投资策略的解析解进行了性质分析；第5 节运用数值模拟来分析相关指标对最优投资策略的影响；第6 节是本文的总结.

2 模型介绍

由于通胀率的波动通常都是受金融市场以外的风险因素所影响，因此它与金融风险有所不同.通常，以消费者价格指数(CPI)来表示通胀率.本文假设通胀指数债券可以自由交易，以满足投资者对冲通胀风险的需求，所以本文假设金融市场为完全市场.

在金融市场中共有三类资产可用于投资，分别为：一个无风险资产，一个股票和一个通胀指数债券.{(B1(t),B2(t),B3(t))}0≤t≤T为完全概率空间(Ω,F,P)上的标准三维布朗运动过程，{Ft}0≤t≤T为该布朗运动生成的σ域流.

无风险资产的价格过程满足

其中R(t)为名义利率，是{Ft}-可测过程，S0(0)=1.

股票的价格变动过程为

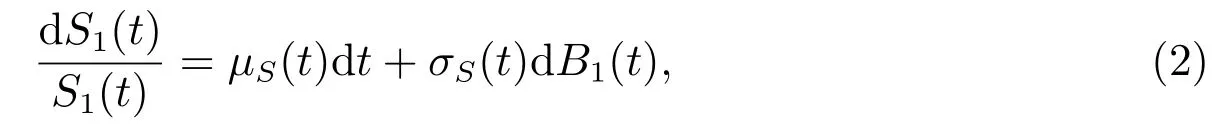
其中µS(t),σS(t)分别为股票的预期收益率和波动率，均为{Ft}-可测过程，且S1(0)＞0.

价格指数满足过程

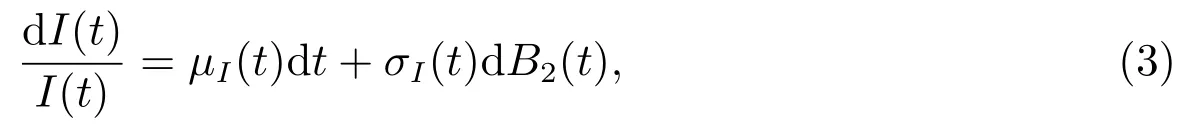
其中µI(t)和σI(t)分别表示预期通胀率和通胀波动率，均为{Ft}-可测过程.

这样，通胀指数债券的价格指数即为

其中r(t)为考虑了通胀影响后的实际利率，为{Ft}-可测过程，(r(t)+µI(t))为该债券的预期收益率.

为了经济均衡，一般假设R(t)＜µS(t).同时，假定B1(t)和B2(t)的相关系数为ρ(t)∈(-1,1)，满足

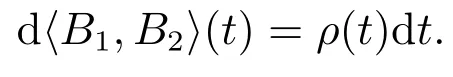
为了方便后文计算，假设存在一个独立于B1(t)的一维标准布朗运动B3(t)，满足

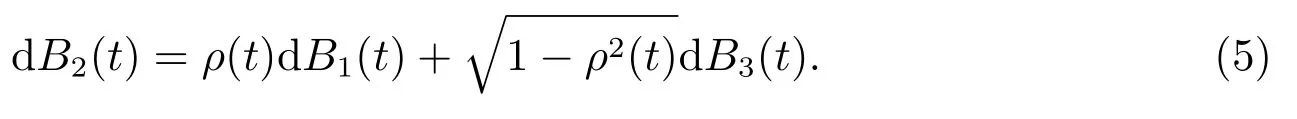
令π0(t),π1(t),π2(t)分别为投资于无风险资产，通胀指数债券和股票的财富比例，若πi(t),i=1,2 为{Ft}-可测过程，则投资组合过程可行，即对于任意T ＜∞，满足

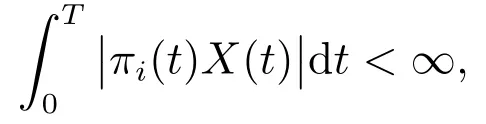
定义可行策略集为Π.

因此，得到名义财富过程如下

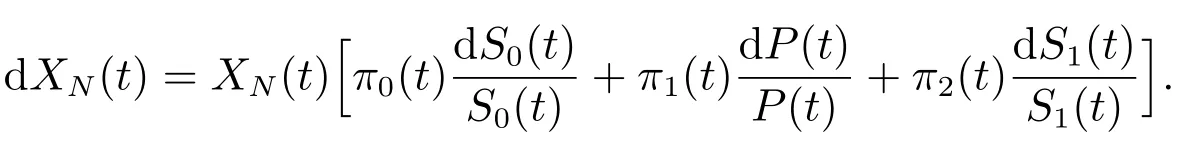
由于投资者的效用函数以实际价值定义，所以需要将名义财富过程转换为实际财富过程X(t),X(t)与XN(t)有如下关系：X(t) =XN(t)/I(t)，对该式运用伊藤公式，可以得到真实财富过程满足以下运动方程

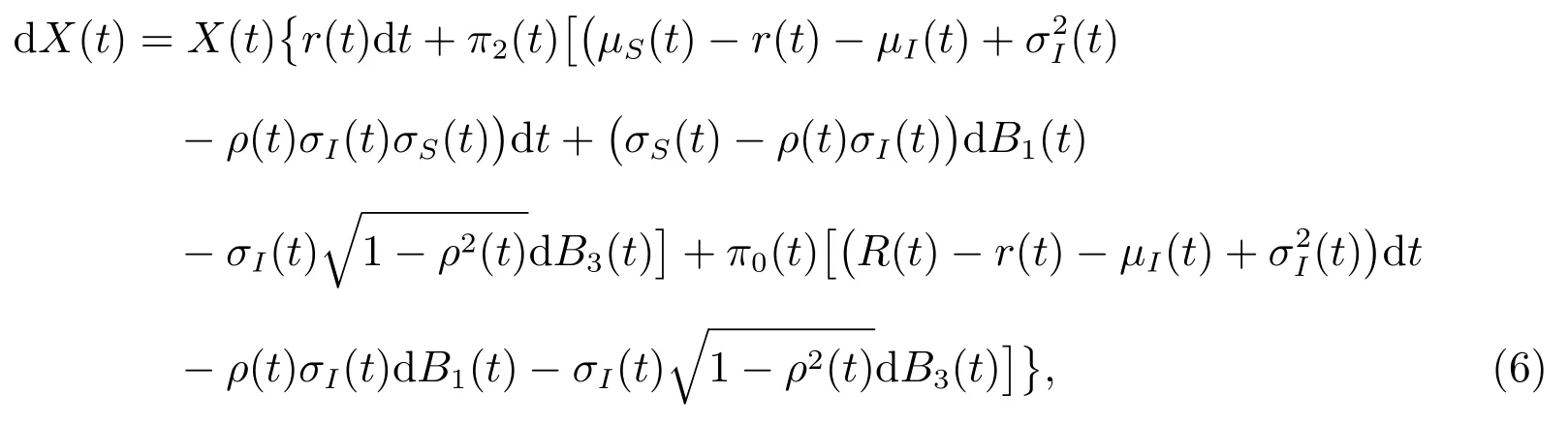
其中X(0)=x为初始财富.

在实际财富过程中，第二项表示投资于股票所带来的实际财富变化，第三项表示投资于无风险资产带来的实际财富变化.

大部分文献中的个人最优投资组合选择决策主要运用的是期望效用最大化模型，并假定效用函数在(0,∞)上是平滑的、凹的、非递减的.而本文使用的则是基于累积前景理论(CPT)下的S 型效用函数，即假设投资者是损失厌恶的.

定义如下

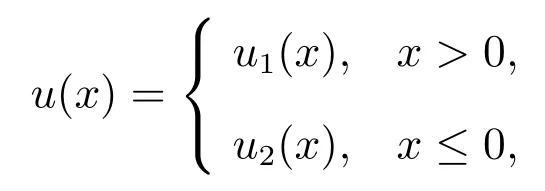
本文中所运用的S 型效用函数为如下的一种特殊形式

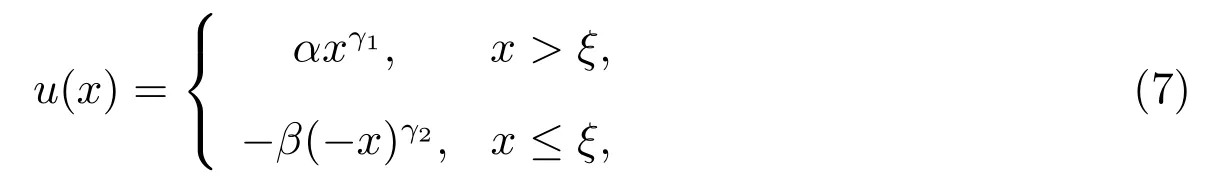
其中0＜γ1≤γ2≤1,β ＞α ＞0，β为投资者的损失厌恶系数.本文将运用Tversky 和Kahneman[4]给出的特例：γ1=γ2=0.88,α=1,β=2.25.

这样，投资者的效用函数U(·)就可以定义为

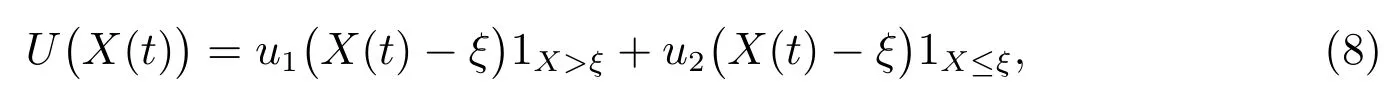
其中ξ ＞0 为一个常数，代表参考点，该参考点决定了最终财富对于投资者而言，究竟是收益还是损失.1 为指示性函数.

设投资者的投资期为T，时间一般为半年以上，是一个中长期的投资.根据效用最大化原理，投资者的最优行为投资决策问题架构如下

其中X(t)≥0,∀t ∈[0,T]表示投资者在投资期[0,T]内不会破产.

3 最优行为投资决策

这一小节，将使用鞅方法来求解(9)中的最优行为投资决策问题，并把(9)中带有预算约束的动态最大化的问题转化为一个静态问题.这样，就可以通过拉格朗日乘子法来求解这个有约束条件的动态最优化问题了.

在完全市场的假设下，会存在唯一的价格核(即折价因子)，定义为

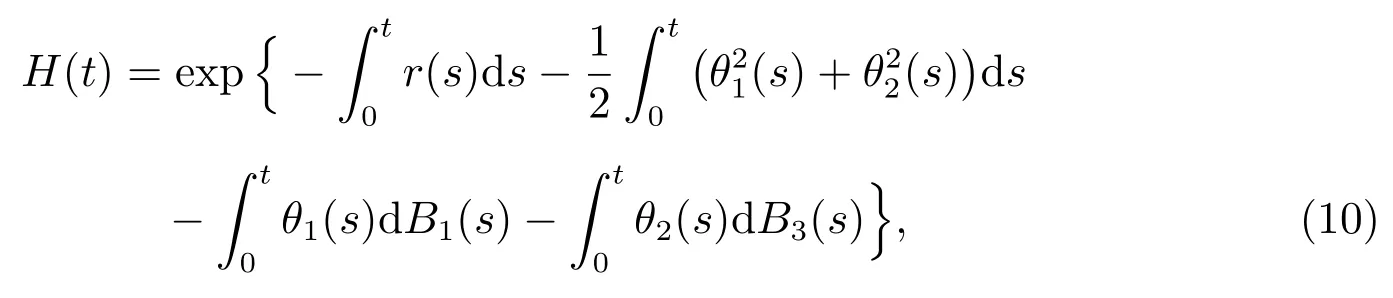
其中θ1(t)和θ2(t)为{Ft}-可测过程，分别定义为

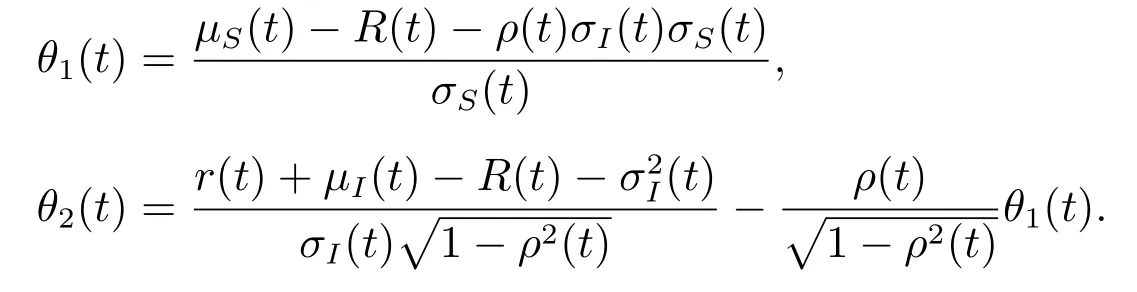
故H(t)有如下微分形式

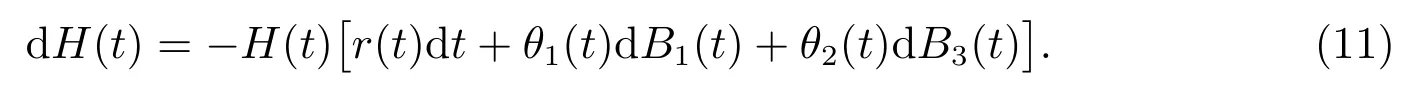
运用伊藤公式，可以得到

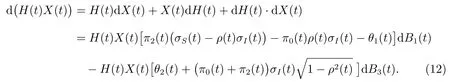
对(12)两边积分可以得到

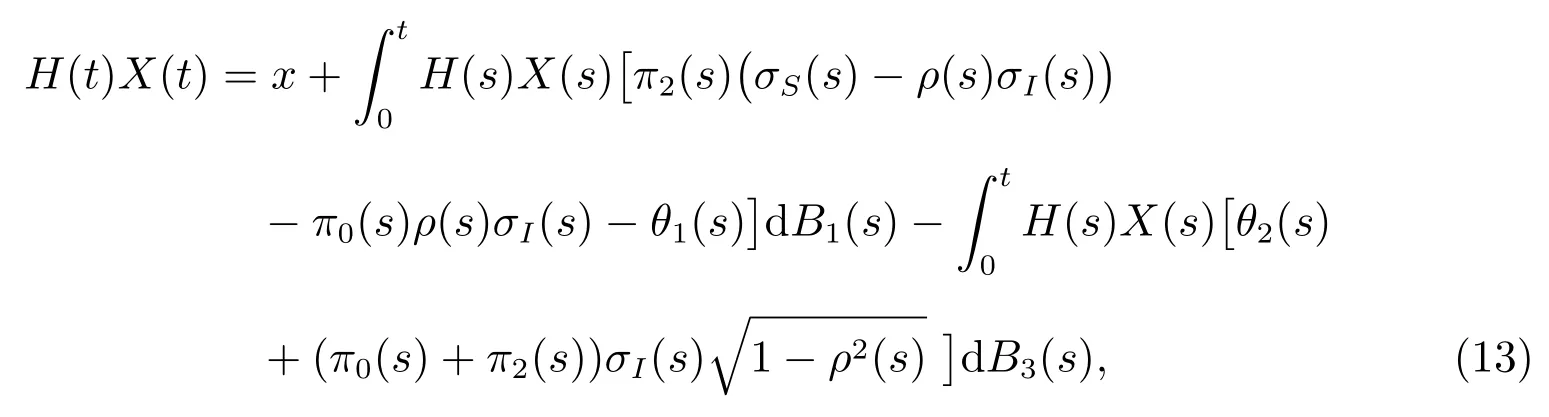
这表明，H(t)X(t)的伊藤积分为两个标准布朗运动的形式，从而是一个P-鞅，同时也是一个上鞅.

根据上鞅的性质，可以得到如下的预算约束条件

该预算约束条件表明，预期最终财富的“折现”值不能超过投资者的初始财富.

定理1给定η ≥0 为{FT}-可测的随机变量，满足：E[H(T)η]=x，则存在投资组合策略(π1(t),π2(t))，使得(π1(t),π2(t))∈Π,t ∈[0,T]，且X(π1(t),π2(t))(T)=η.

证明 定义M(t)=E[H(T)η|Ft]为鞅，根据鞅表示定理，存在{Ft}-可测过程φi,i=1,2 满足

使得

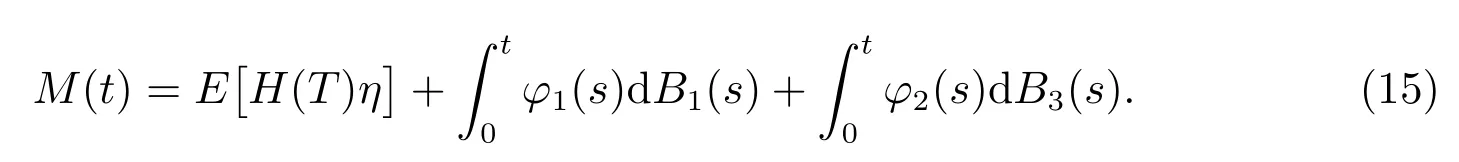
同时

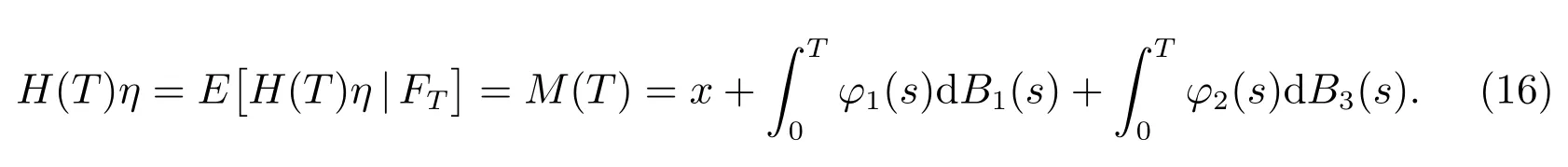
在(13)式中，取t=T，分别与(16)中的dB1(t)和dB3(t)项进行对比，得到

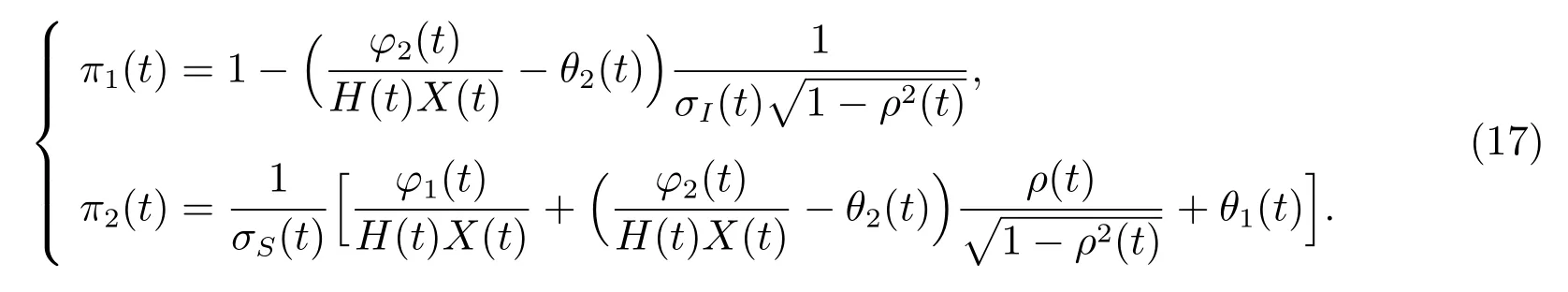
为了检验(π1(t),π2(t))∈Π,t ∈[0,T]，需要证明

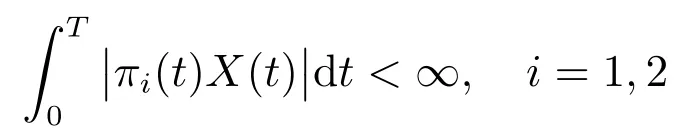
成立.

定义

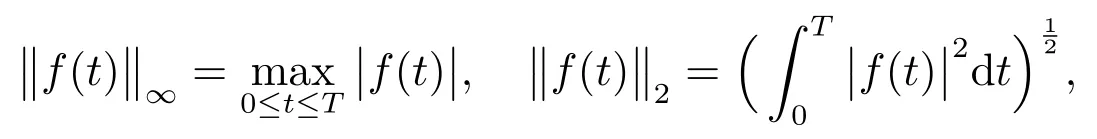
可得

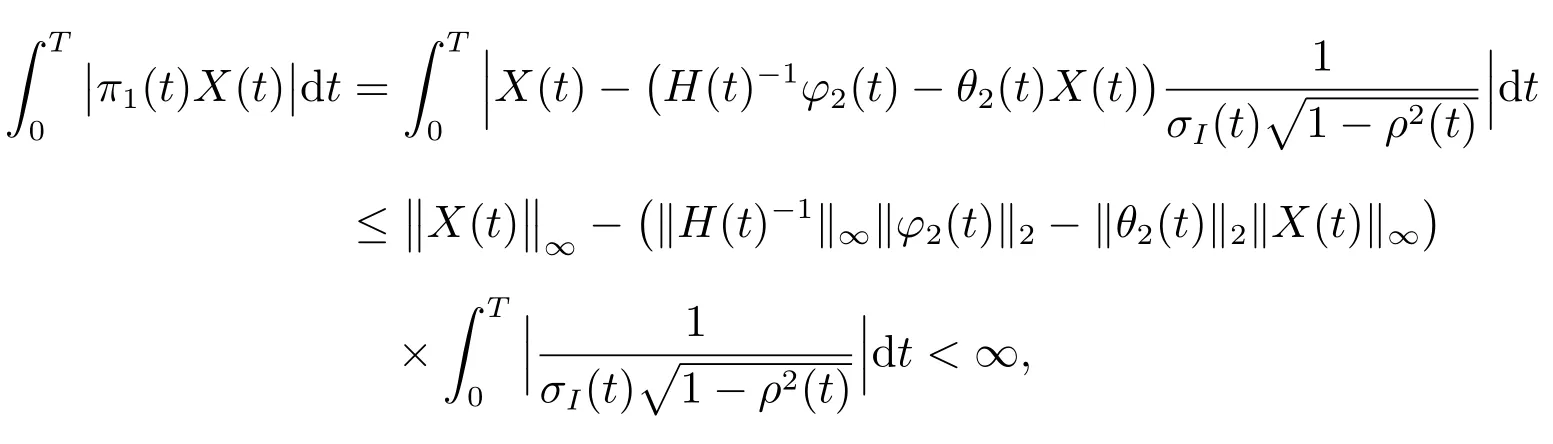
其中

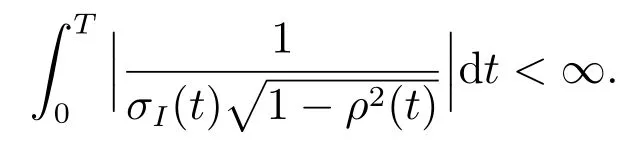
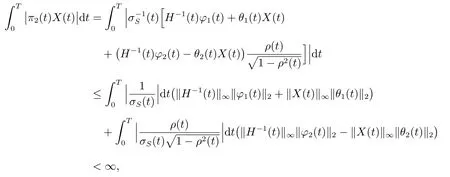
其中

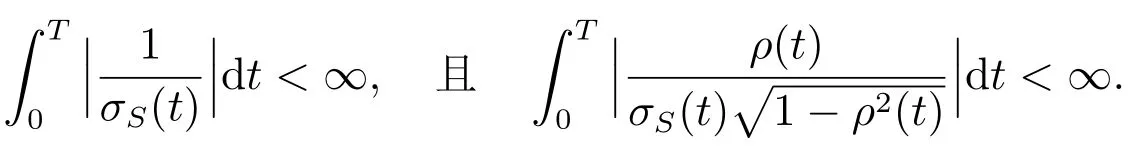
满足

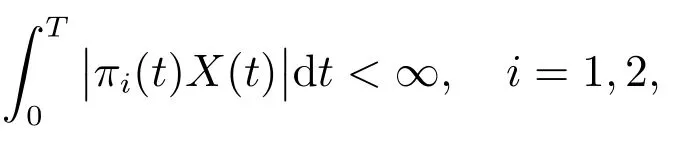
定理1 得证.

根据定理1，之前的动态最优化问题就等同于下面的静态最优化问题

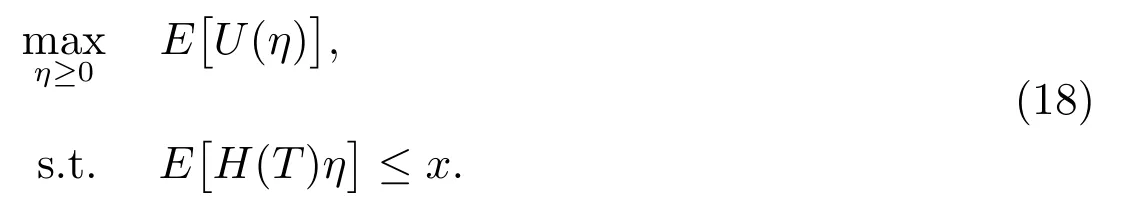
根据文献[9]讨论得出的结果，可以得到(18)的结果如下

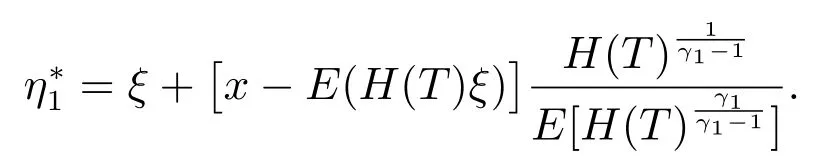
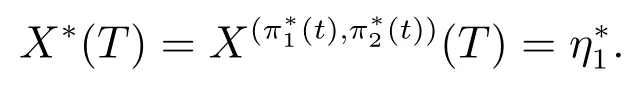
与H(T)相乘，并对两边取条件期望，可以得到

根据H(t)X(t)为上鞅，可以将(20)改写为

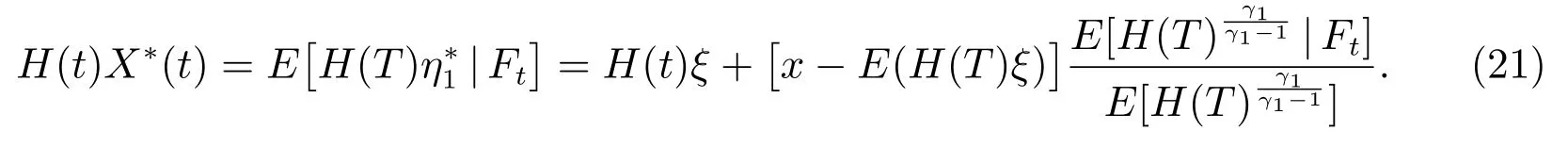
引入指数鞅如下

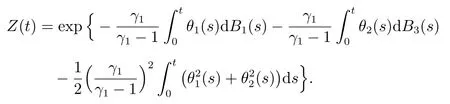
根据Z(t)，可以将改写为

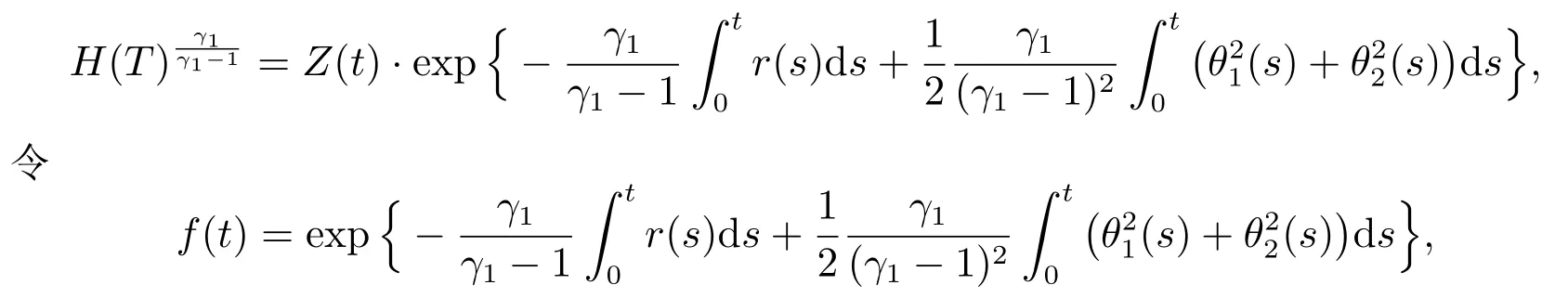
则(21)的右半部分可以改写为

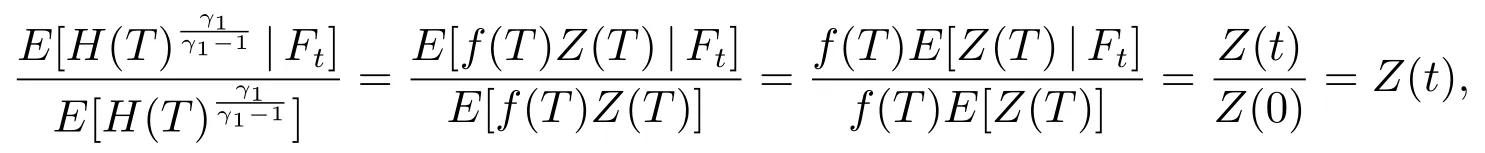
其中Z(0)=1.将其代回到(21)，又因为可以得到

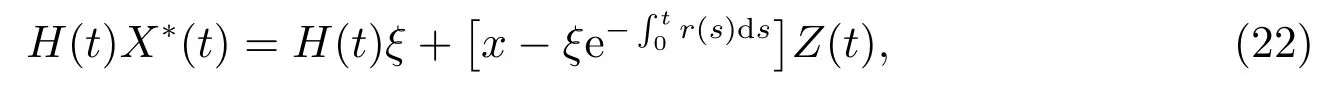
对(22)两边求微分，得到

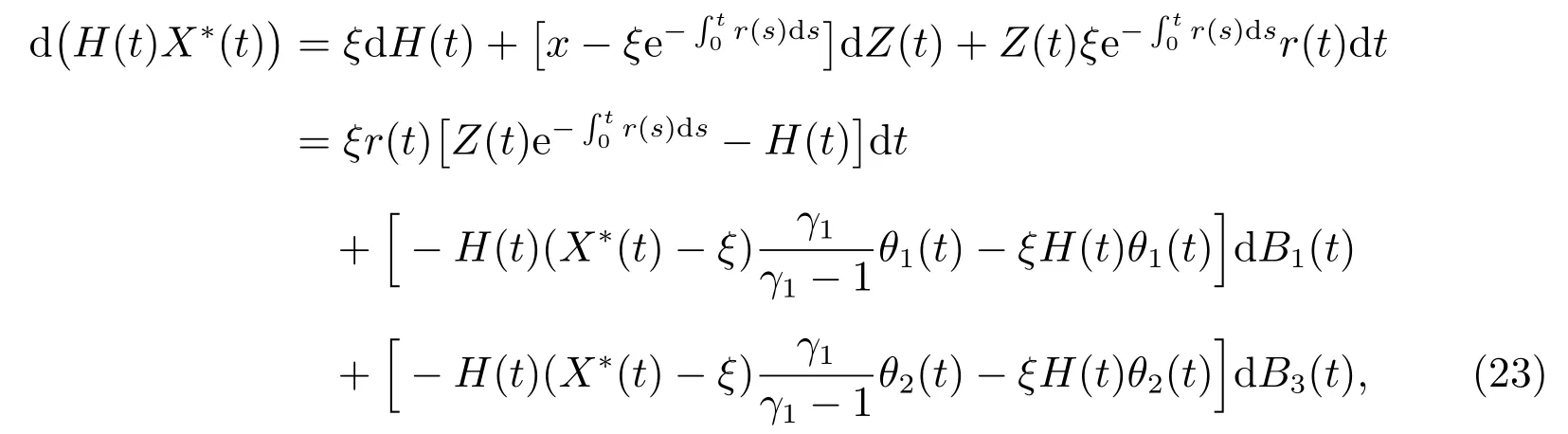
因为H(t)X∗(t)也满足(12)，给出如下

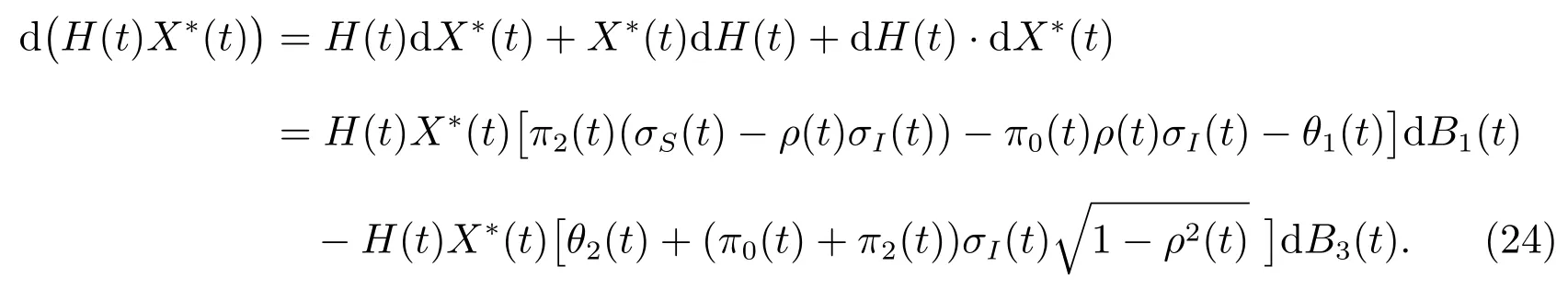
对比(23)和(24)的扩散项，可以得到

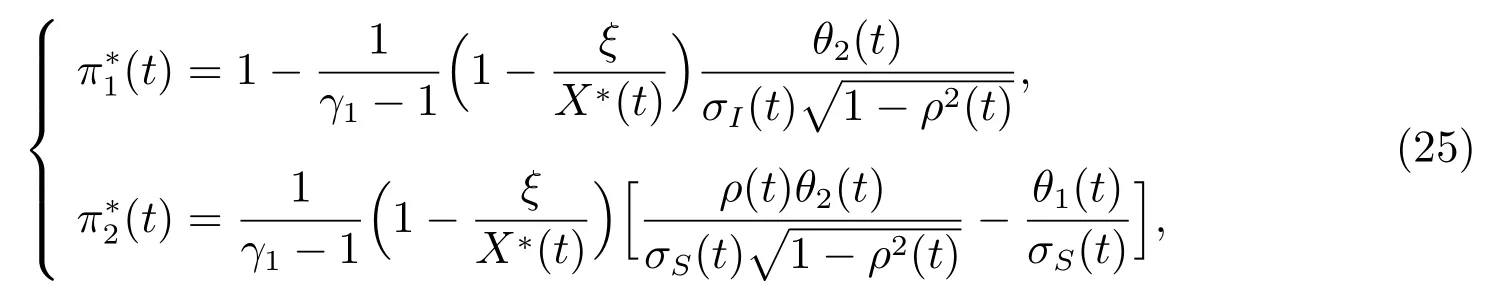
其中θ1(t),θ2(t)如前定义.

根据(22)，可以得到最优财富过程如下

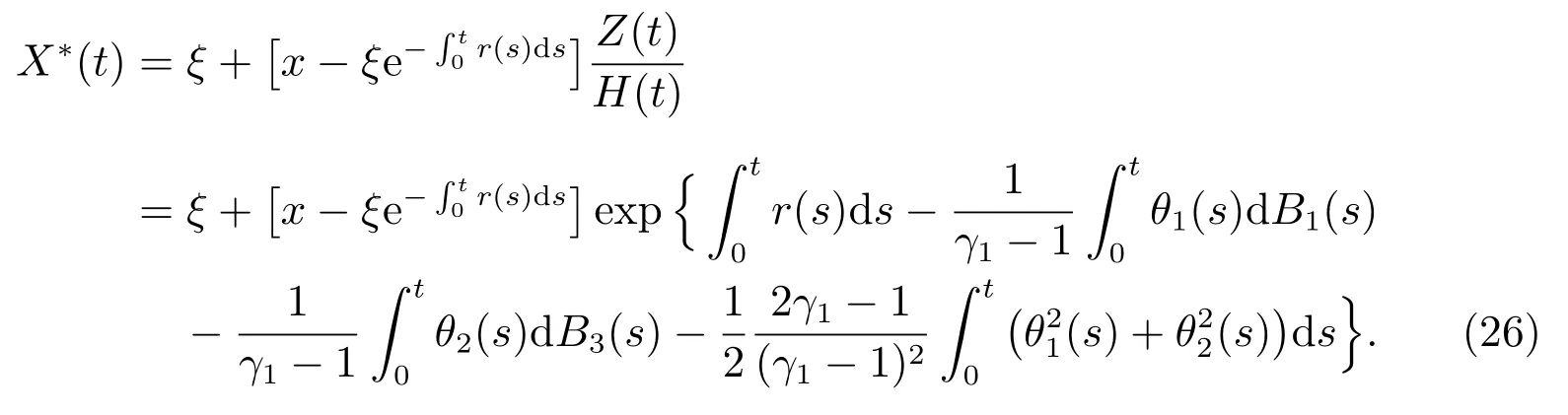
同时，可以得到最优期望效用如下

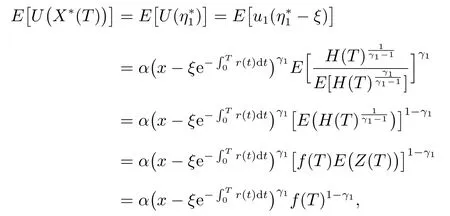
其中E(Z(T))=1，将f(t)代入，投资者最终财富的最优期望效用为

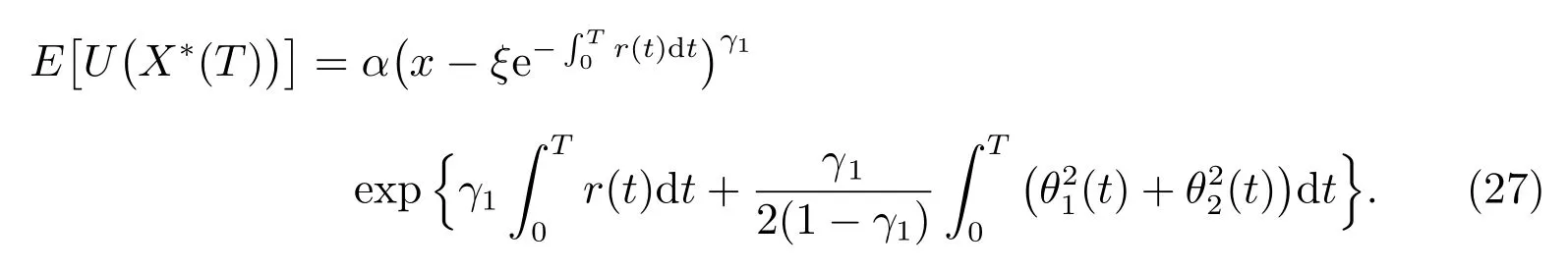
定理2在有通胀风险的市场条件下，研究个人的最优投资决策问题，并假设投资者具有损失厌恶的行为特质，那么，最优投资策略t ∈[0,T]给出如下

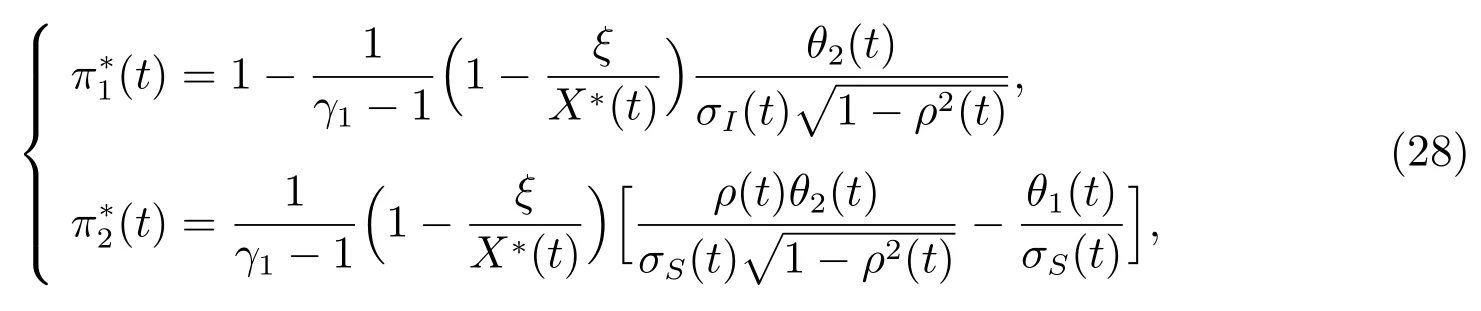
其中θ1(t),θ2(t)如前定义.

对应的最优财富过程X∗(t),t ∈[0,T]满足

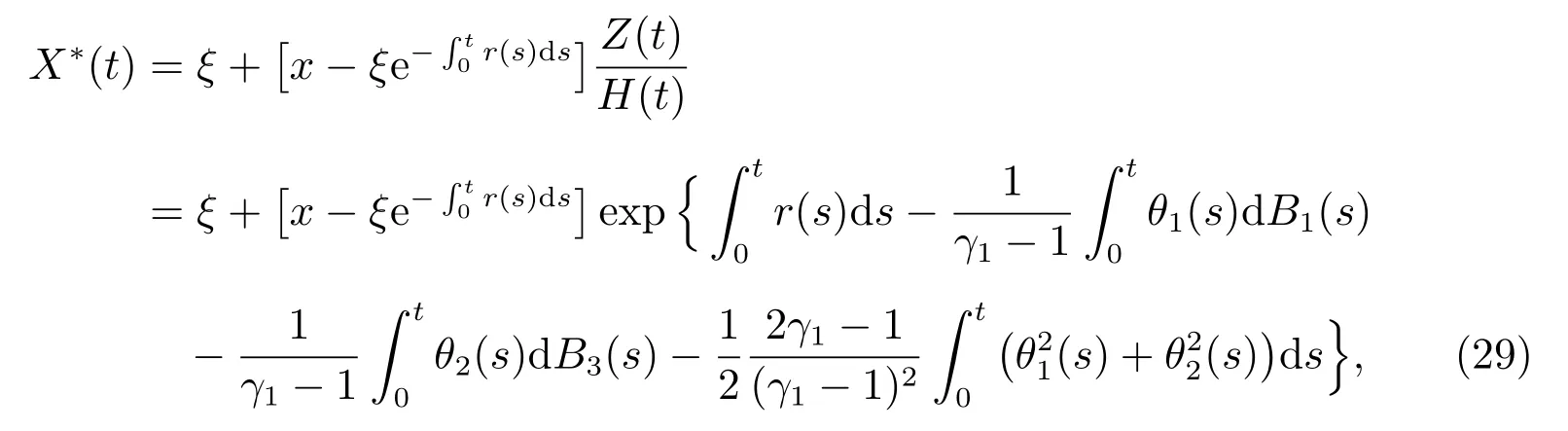
且最终财富的最大期望效用由(27)给出.

4 最优投资策略性质分析

根据(25)所得到的最优投资策略的解析解，可以进行进一步的性质分析，尤其是预期通胀率µI(t)、通胀波动率σI(t)、相关系数ρ(t)和参考点ξ的变化，对最优投资策略所带来的影响.定义(名义)通胀风险溢价为PI(t) =R(t)-µI(t)-r(t)，(名义)股票溢价为PS(t) =µS(t)-R(t)，并假设股票溢价为正.分别对µI(t),σI(t),ρ(t) 和ξ求偏导，可以得到

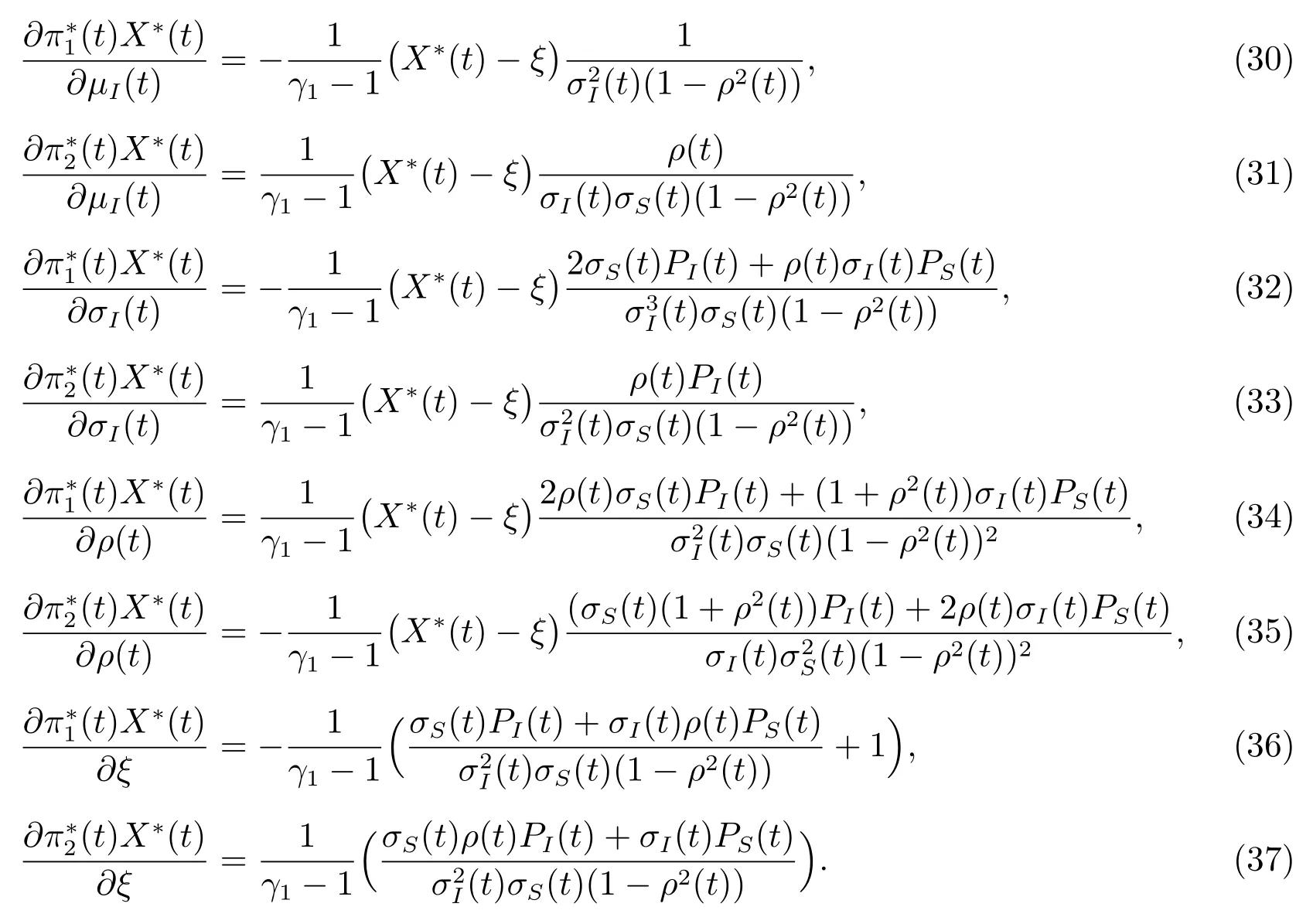
由(30)可知，当市场出现较高的预期通胀率的时候，投资者会增加在通胀指数债券上的投资.

由(31)可知，预期通胀率对股票需求的影响仅仅取决于相关系数ρ(t)，如果ρ(t)＜0(即通胀指数债券和股票负相关)，当预期通胀率升高时，投资者将在增加通胀指数债券投资的同时，更多地投资于股票来进行多样化投资；如果ρ(t)＞0(即通胀指数债券和股票正相关)，投资者在增加通胀债券投资的同时，将减少股票投资，来分散风险；如果ρ(t)=0，预期通胀率对股票需求没有影响.

由(32)可知，通胀波动率σI(t)对通胀指数债券的需求影响取决于相关系数ρ(t)和通胀风险溢价PI(t).若两者符号相反，那么就无法确定通胀波动率对通胀指数债券需求的影响；若两者符号同为非正，那么通胀波动率越大，就应该越少投资于通胀指数债券；若两者符号同为非负，那么情况相反.

由(33)可知，通胀波动率σI(t)对股票的需求影响也取决于相关系数ρ(t)和通胀风险溢价PI(t).若两者符号相反，那么通胀波动率越大，投资于股票的份额就越高；若两者符号相同，那么情况相反.

由(34)可知，相关系数ρ(t)对通胀指数债券的影响取决于相关系数ρ(t)和通胀风险溢价PI(t).若两者同号，或两者异号，且

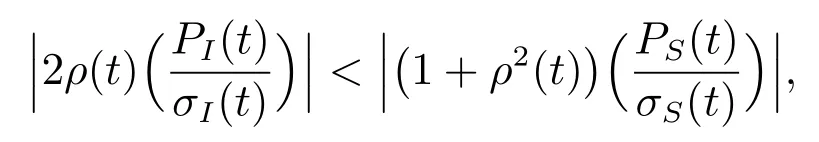
由于大部分情况下股票溢价高于通胀风险溢价，故该式在大多数现实市场环境中成立，那么也就是说，相关系数越高，分散投资效果不佳，所以会带来较少的通胀指数债券投资.

由(35)可知，相关系数ρ(t)对股票的需求影响取决于相关系数ρ(t)和通胀风险溢价PI(t).若两者符号相反，那么就无法确定相关系数对股票需求的影响；若两者符号同为非正，那么相关系数越大，股票投资越少；若两者符号同为非负，那么情况相反.

由(36)可知，参考点ξ对通胀指数债券的需求影响取决于相关系数ρ(t)和通胀风险溢价PI(t).若两者符号相反或同为非正，那么难以确定参考点对通胀指数债券的影响；若两者符号同为非负，那么参考点越大，通胀指数债券投资越多.

由(37)可知，参考点ξ对股票的需求影响取决于相关系数ρ(t)和通胀风险溢价PI(t).若两者同号，或者，两者异号，且

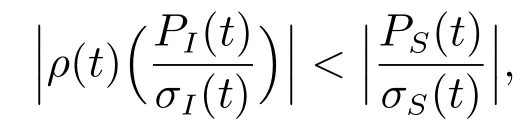
同样，由于大部分情况下股票溢价高于通胀风险溢价，故该式在大多数现实市场环境中成立，则

随着参考点的提升，股票需求减少.

5 数值模拟

在这一节，考虑到相关变量变化对最优投资策略影响的复杂性，无法通过理论分析直接得到，拟通过数值分析方法，研究预期通胀率µI、通胀波动率σI、相关系数ρ和参考点ξ对最优投资策略的影响.为此，假设初始真实财富为X(0) =x= 10 万元，名义利率R= 0.04，实际利率r= 0.02，股票的预期收益率和波动率分别是µS= 0.08 和σS=0.3，预期通胀率µI= 0.023，通胀波动率σI= 0.15,γ1= 0.88，两类资产的相关系数ρ=-0.07，参考点ξ=9.

从图1 可以看出，随着预期通胀率µI的增加，损失厌恶的投资者将选择通过购买通胀指数债券的方式来进行风险规避，通胀指数债券的需求不断增加.在ρ=-0.07＜0 的情况下，由于通胀指数债券和股票呈负相关，投资者也稍增加了对股票的投资来进行多样化投资，但增长较不明显.同时，无风险投资的减少主要被转移到了通胀指数债券的投资上.因此，预期通胀率的变化对股票影响较少，投资者主要根据预期通胀率的多少，在无风险投资和通胀指数债券之间进行选择.

从图2 可以看出，当预期通胀率µI= 0.023 时，股票需求相对于相关系数的变化是U 型的：当ρ ＜0 时，随着相关系数的减少，投资者将增加对于股票的投资来进行多样化投资，分散风险；相反，当ρ ＞0 时，随着相关系数的增加，投资者将减少股票投资；而当ρ= 0 时，预期通胀率对股票需求则没有影响.在ρ=-0.07＜0 的情况下，随着预期通胀率µI的增长，投资者也适当地增加了对股票的投资来进行多样化投资.

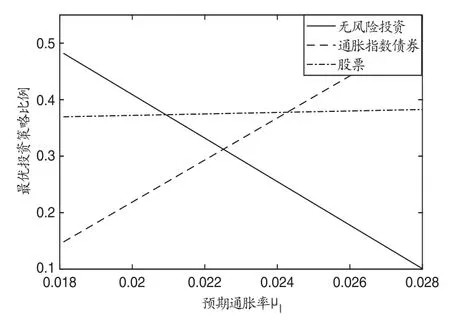
图1: 预期通胀率µI 对最优投资策略的影响

图2: 预期通胀率µI 对股票需求的影响

从图3 可以看出，随着通胀波动率σI增大，通胀指数债券收益不确定性增大，作为损失厌恶的投资者，在这种情况下，将减少对通胀指数债券的投资.同时，股票需求基本不变，所以，减少的那部分投资则主要转移到了无风险资产的投资上去.因此，当投资者面对通胀波动率的变化时，将不会影响其对股票的投资，而是在无风险投资和通胀指数债券之间进行权衡.这与预期通胀率变动的结论相仿，故得出：在考虑通胀风险的情况下，投资者将不会对股票的投资进行大的变动，而是在无风险投资和通胀指数债券之间进行选择来规避通胀风险.同时，股票的轻微变动主要是由通胀指数债券及股票的相关性所带来的，目的是为了更好地分散风险，进行多样化投资.

由于股票投资不随通胀风险相关指标的变动而变化，在此，通胀指数债券的功能主要体现为股票投资的补充投资手段，即起到多样化投资的作用.从图4 可以看出，相关系数越高，投资者会减少通胀指数债券投资来分散风险，而相关系数越低，投资者会增加通胀指数债券投资来进行多样化投资.

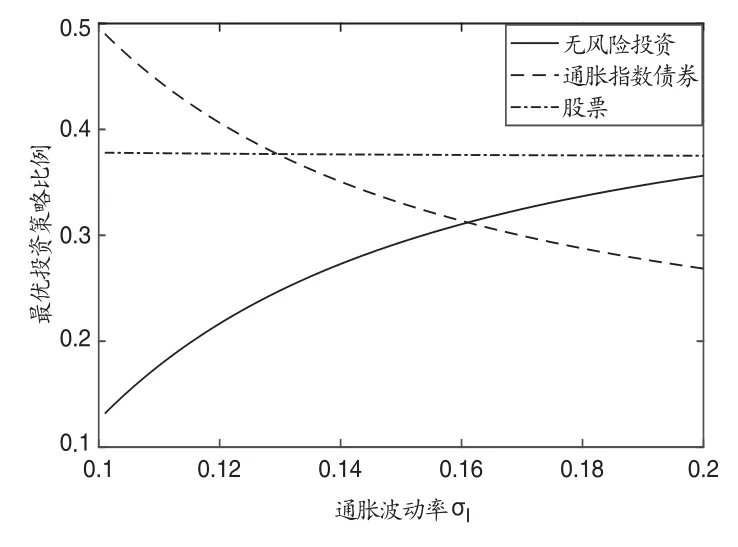
图3: 通胀波动率σI 对最优投资策略的影响

从图5 可以看出，随着参考点的增加，通胀指数债券投资增加，而无风险投资与股票投资减少.参考点越高，即说明投资者判断收益损失的盈亏点就越高.而股票作为风险较大的投资，面对较高的收益要求，并不是损失厌恶的投资者的最佳选择.而通胀指数债券的风险较小，且能起到对冲通胀风险的作用，可以减少投资者的损失，因此，作为损失厌恶的投资者会选择增加对通胀指数债券的投资.之前结论提到，在考虑通胀风险的情况下，投资者将会在无风险投资和通胀指数债券之间进行选择，因此，在增加通胀指数债券投资的同时，无风险投资也在减少.

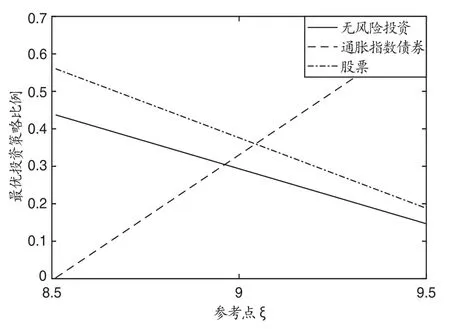
图5: 参考点ξ 对最优投资策略的影响

6 结论

考虑通货膨胀的影响，本文研究了个人最优行为投资决策问题.假设投资者是损失厌恶的，并用累积前景理论中提出的S 型效用函数来刻画投资者的这一行为特质.在此基础上，引入通胀指数债券来对冲通胀风险，建立了个人最优行为投资模型.通过鞅方法求解出了最优投资策略以及最终财富的解析解，并根据合理的市场参数进行了数值模拟，得到了以下结论：

1) 在考虑通胀风险的情况下，投资者将不会对股票的投资进行大的变动，而是在无风险投资和通胀指数债券之间进行权衡选择来对冲通胀风险.随着预期通胀率的增加，投资者将增加通胀指数债券的购买来进行风险对冲.随着通胀波动率增大，收益不确定性增大，损失厌恶的投资者将减少对通胀指数债券的投资；

2) 当通胀指数债券作为一种新的投资手段时，起到了多样化投资的作用.当通胀指数债券和股票相关系数越高时，投资者会减少通胀指数债券投资来分散风险，而相关系数越低时，投资者则会增加通胀指数债券投资来进行多样化投资；

3) 随着参考点的增加，投资者会增加通胀指数债券的投资来对冲风险，减少损失，同时，减少对无风险投资与股票的投资.

虽然本文对带有通货膨胀风险的个人最优行为投资决策问题进行了较为详尽的分析，但仍然存在一些研究的局限，比如没有考虑到个人的消费、收入等过程，为了方便计算，假设也相对简单.因此，当研究假设更贴近现实生活时，相关结果如何，仍是需要解决的研究课题，也是研究人员在未来拟开展的研究方向.