带五次项的非线性Schrödinger方程的守恒差分格式
李 华,李德生
(沈阳师范大学 数学与系统科学学院,辽宁 沈阳 110034)
0 引言
非线性Schrödinger方程(NLS)是非线性光学、等离子物理等领域的重要数学物理模型.对该方程的数值研究已经取得了丰富的成果[1-5],如有限差分法、有限体积法、有限元法、离散变分导数法等.其中离散变分导数法具有保结构等优点而日益受到人们的关注.文献[6]用离散变分导数的方法对NLS方程提出了一个守恒差分格式,基于此,笔者应用[6]的思想,对带五次项的非线性Schrödinger方程[7]
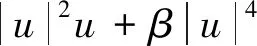
(1)
u(x,0)=u0(x),x∈(0,L),
(2)
u(x,t)=u(x+L,t),t∈(0,T),
(3)
构建其保结构的差分格式.其中α<0,β<0,i2=-1,u(x,t)为复值函数,u0(x)为已知的复值函数.该问题的电荷和能量满足下列关系:
(4)
(5)
其中Q(t),E(t)分别称为某时刻的电荷和能量,Q(0),E(0)分别称为初始时刻的电荷和能量,(4)称为电荷守恒,(5)称为能量守恒.
1 相关符号的定义
本文中使用的记号如下:
xk=kΔx,tm=mΔt,k=0,1,…,N,m=0,1,…,M.
空间位移算子为
s+k=fk+1,s-k=fk-1,
空间平均算子为
时间方向相关算子可以类似定义.本文应用的内积与范数定义为
为简单起见,当p=2时,我们省略下标,并定义umk和Umk分别为u(x,t)在(kΔx,mΔt)处的精确解和数值解.定义C为正常数,在不同的地方可以表示不同的值.
求和公式应用梯形法则:
2 差分格式的建立
将方程(1)改写为
(6)
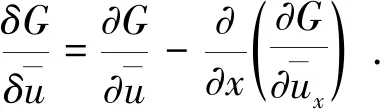
由此,可以定义局部能量函数G,整体能量函数J:
(7)
(8)
故定义离散局部能量
(9)
其中下标d表示离散,k表示空间方向.
下面求离散变分导数,运用直接因式分解法,有
其中(c.c)表示前一项的复共轭,Bc(Um+1k,Umk)表示边界条件,且有
(10)
因此,可得离散变分导数
(11)
综上,可得最终格式为
(12)
3 差分格式所继承的守恒性质
正如在引言中提到的,该方程具有电荷守恒和能量守恒的性质,即
电荷守恒证明如下:
(13)
其中边界项由于周期边界条件消去了.
能量守恒证明如下:
(14)
其中边界项亦由于周期边界条件消去了.
离散情况下,给定的差分格式也具有守恒性质.
定理1 在离散的周期边界条件下,差分格式的解Umk满足
(15)
证明
最后一个等号是把离散变分导数的具体形式代入并用逐段求和公式
即可得出结论.
类似地,可以证明
(16)
4 解的存在唯一性以及解的估计

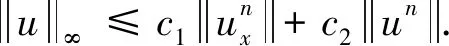
定理2 该差分格式存在唯一解.

显然,g是连续的.还可以得到
其中最后两项为纯虚数,第3项根据逐段求和公式,我们有
因此这一项也是纯虚数.因此,我们可得
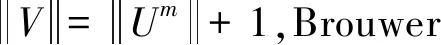
下面证明唯一性.
假设该格式存在2个解V和W,为了证明唯一性,则只需证V=W.
由Vk的表达式,易求得
应用逐段求和公式,有
根据实部和虚部,有

综上,解的存在唯一性得证.

(17)
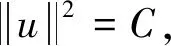
5 解的收敛性
这里定义截断误差为Fmk,
(18)


(19)

(20)

接下来证明格式的收敛性,定义数值解的误差为
emk=umk-Umk.
(21)
定理4 当u∈C2([0,T],C3]时,存在常数c,只要1-cΔt>0,就有
(22)
当u∈C2([0,T],C5]时,存在常数c′,只要1-c′Δt>0,就有
(23)
证明用(18)式减去(12)式,可以得到
(24)
左端变成了
(25)
右端第1项为0.
(24)式右端第2项可以改写为

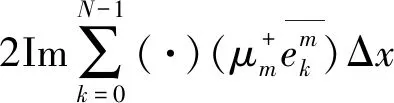
(26)
右端第4项
综上,有
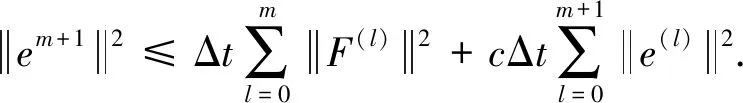
当Δt满足1-cΔt>0时,
再由引理3和引理4,该格式的收敛性得证.
6 结论
笔者应用离散变分导数法,构建了带五次项的非线性薛定谔方程的一个保结构的差分格式,证明了该格式解的存在唯一性,稳定性,以及该格式在一定条件下的收敛性.

