基于ARIMA和马氏链模型的中国财政收入预测
侯甜甜,杨 丛,詹炳欢
(平顶山学院 数学与统计学院,河南 平顶山 467036)
0 引言
关于中国近期及中期财政收入预测分析等相关论文,大多数采用中国财政收入年度数据,并利用多元线性回归模型预测.作为发展中国家的中国,其财政收入情况一直备受瞩目,近几年来中国财政收入的增长速度迅猛,很多国内外经济学、统计学专家都对中国财政收入进行了深入研究,大量期刊类文章对中国财政收入进行多角度、多层面的理论分析,涉及较深的经济学理论.目前缺少利用纯数学的方法对中国财政收入进行高准确度预测,基于时间序列对中国财政收入进行预测,在数学预测中已经广泛应用,但是基于马氏链模型对中国财政收入的预测,国内并没有深入研究.笔者通过ARIMA模型和马氏链模型对中国财政收入进行预测.
时间序列分析的应用方法已经相当成熟,应用领域也很广泛,时间序列分析中的ARIMA模型在经济、商业预测中具有重要地位.例如:2016年卓鹏宇的基于时间序列分析的股票趋势预测模型研究、2018年任慧的 ARIMA模型在中国人均GDP预测中的应用和2017年刘伟霞的ARIMA模型在福建省第三产业产值预测中的应用,都是近几年ARIMA模型在经济和商业预测中的经典应用.时间序列在以前的巨大贡献更是不胜枚举,其应用领域也是扩展到除经济和商业领域外的医学、气象、水安全、人文等领域.
马尔科夫过程在随机过程理论中具有重要地位,它的应用范围也极其广泛,包括物理、生物学、水资源科学、气象科学、地质科学等各个领域.20世纪初,马氏链的创造者马尔科夫提出并研究一种用数学分析方法研究自然过程的模型,也叫马氏链模型.他推动了概率论的发展,同时他研究的随机过程也被称为马尔科夫过程.马氏链模型被广泛应用于短期的金融预测,对于当下炙手可热的股票和期货等交易中起到了重要的决策作用.2013年夏莉、黄正洪的马尔科夫链在股票价格预测中的应用、王璇的基于马氏链的市场占有率预测分析和罗海玲、郑根的基于R语言股票市场收益的预测分析等,在现代经济、商业中运用最为广泛.笔者对具有周期性和季节性的中国财政收入月度数据进行预测,同时也是一次对中国财政收入预测很有价值的尝试.
1 预测方法
1.1 ARIMA模型介绍
1970年Box和Jenkins提出ARIMA模型,又称差分整合移动平均自回归模型.ARIMA模型对扰动项进行建模分析后,综合考虑预测变量的过去值、当前值和误差值,以此提高模型的预测精度.
具有如下结构的模型称为求和自回归移动平均模型,简记为ARIMA(p,d,q)模型[1]:

当序列具有季节效应,季节效应本身具有短期相关性时,季节相关性可以使用以周期步长为单位的ARMA(P,Q)模型提取.由于短期相关性和季节效应有乘积关系,所以模型为ARMA(p,q)和ARMA(P,Q)的乘积.则拟合的乘积季节模型简记为ARMA(p,d,q)×(P,D,Q)S,结构如下[1]:
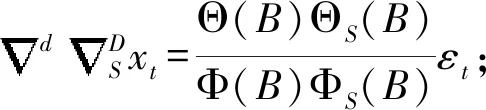
差分观察值序列平稳后,需要判断序列是否有分析价值,因此在建模之前需要进行纯随机性检验,即白噪声检验.检验结果显示是白噪声序列,则该序列没有分析价值;如果是非白噪声序列,则可以进行模型拟合.
对于平稳非白噪声序列Xt,AR模型,MA模型和ARMA模型的自相关系数(ACF)、偏相关系数(PACF)表现出不同的统计特征.根据其截尾性和拖尾性可初步判断出序列所能拟合的模型:AR(p)模型、MA(q)模型、ARMA(p,q)模型的自相关系数和偏自相关系数特征(表1).

表1 不同模型的ACF和PACF特征
由表1自相关系数和偏自相关系数的特征可以初步判定模型所属的类别.然后确定模型的阶数.确定ARMA模型阶数常用的方法有自相关系数和偏自相关系数定阶法以及AIC准则法.
如果ACF在q步截尾,PACF在p阶之后为零并具有拖尾性,则利用MA(q)模型拟合;如果PACF在p步截尾,ACF在p阶之后为零并具有拖尾性,则利用AR(p)模型拟合,如果PACF和ACF都拖尾,则利用ARMA模型拟合.对于ARMA模型,不能确定其阶数.建立ARMA模型时,p和q一般比较低,所以可以尝试确定p和q的值来定出模型,并检验模型是否通过残差白噪声检验,如果没有通过检验,则需调整p和q值,重新建立模型并检验,直至模型通过残差白噪声检验为止.
模型的检验主要从以下几个方面判断:
1)所有的系数是否都显著不为零.
2)残差序列是否为白噪声.
检验残差序列是否为白噪声序列,分别对各模型进行残差白噪声检验,结果显示p值均大于显著性水平,则接受原假设,认为残差序列是白噪声序列.结果显示p值均小于显著性水平,则接受原假设,分析结束.
3)预测是否准确.
4)是否有更大的拟合优度和更小的AIC值和BIC值.
当存在一个p和q使AIC信息量最小时,这时的p和q便是模型理想的阶.主观上认为模型拟合得越准确越好,如果准确度高的同时模型复杂度高,则导致模型拟合困难,从而会影响拟合结果,所以对拟合精度和参数个数进行权重分配.当表示模型拟合好坏的部分发挥主要作用时,AIC的值会显著下降,当模型阶数增加到一定程度时,模型拟合残差减小的效果逐渐变弱,AIC值上升.当模型取到最佳阶数时,AIC的值也应该是最小的.
1.2 马氏链模型
马尔科夫链[2]是由有限个马尔科夫过程构成的,该过程要求具备“无后效性”,“无后效性”是指状态转移过程中从一个状态转移到另一个状态,下一状态只与当前状态有关,与之前的状态无关.满足这个特征的随机过程才被称为马尔科夫过程.
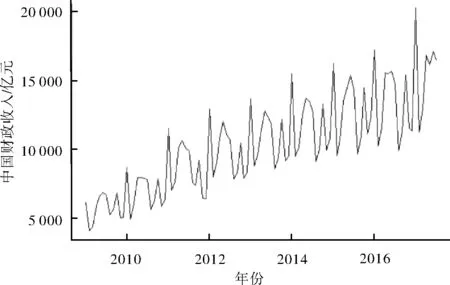
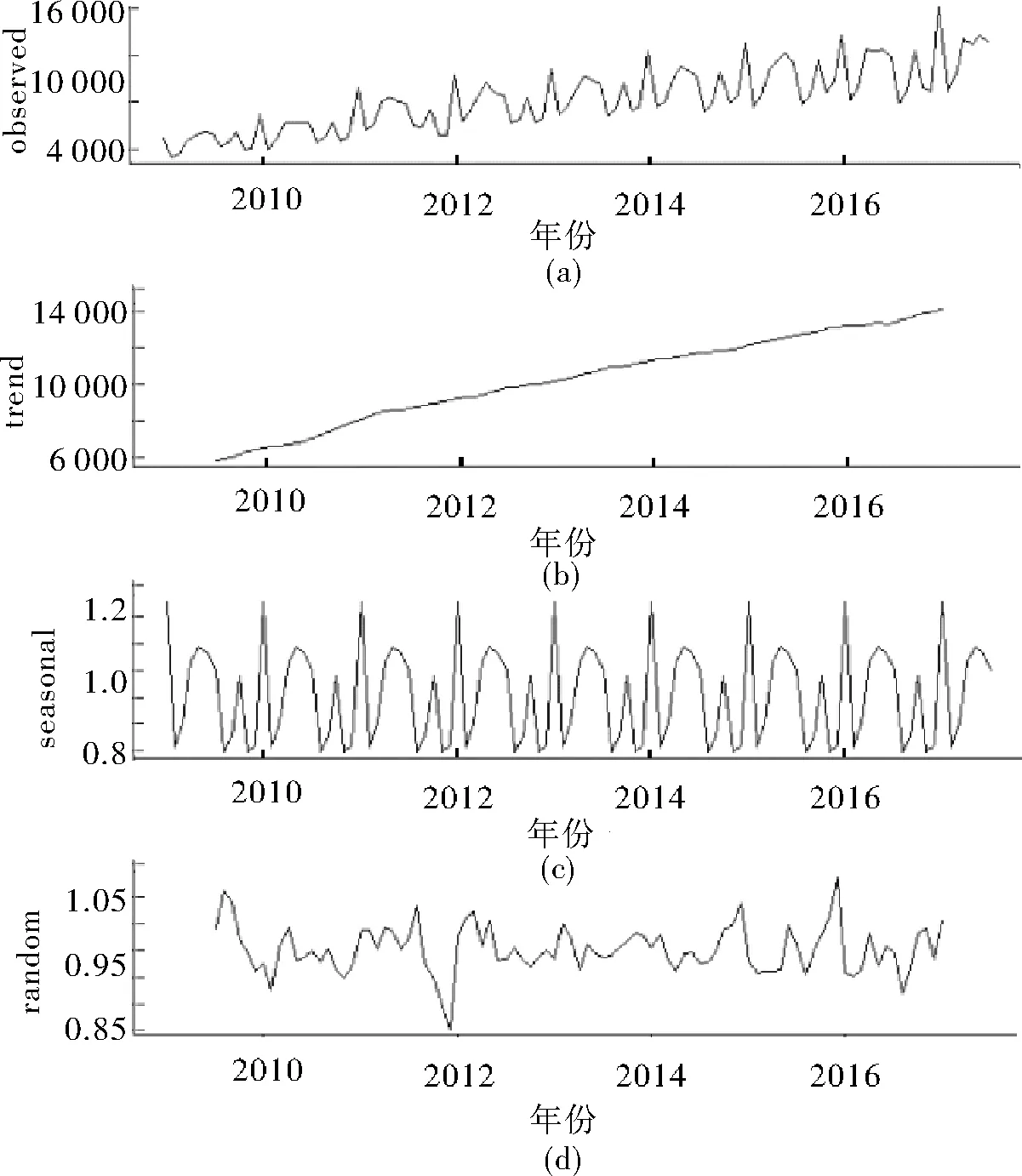
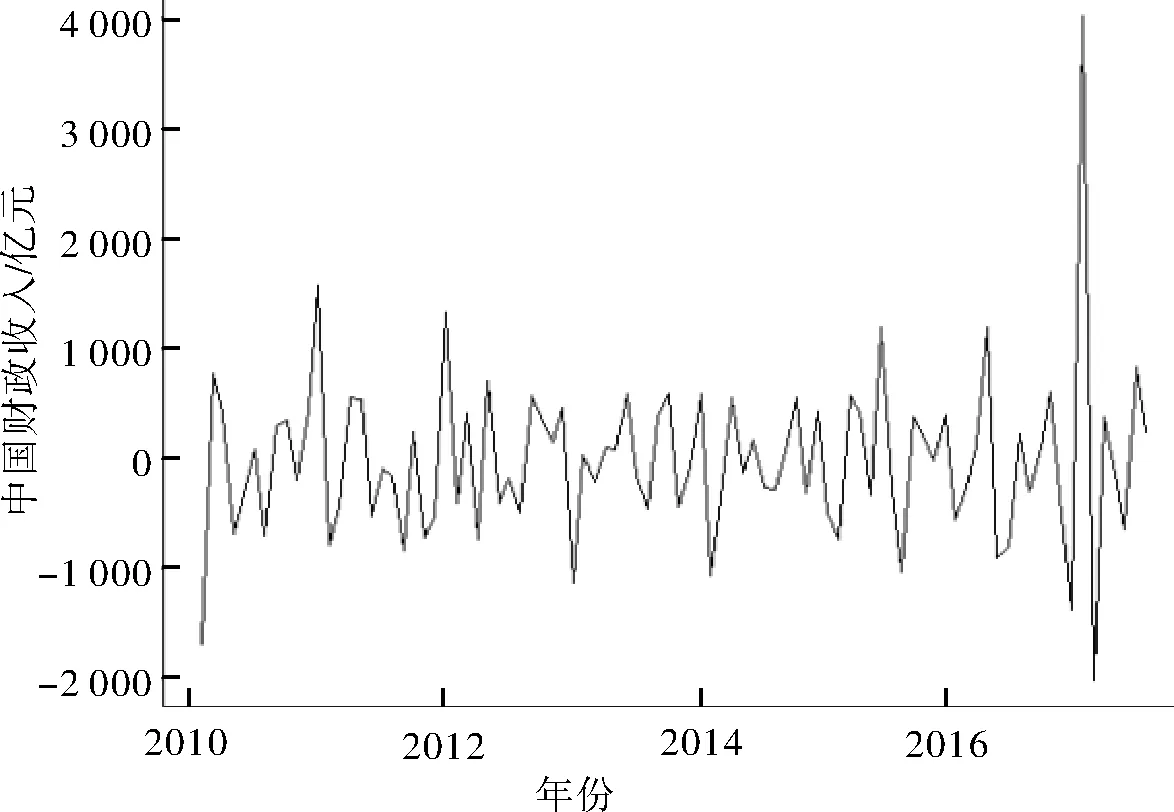
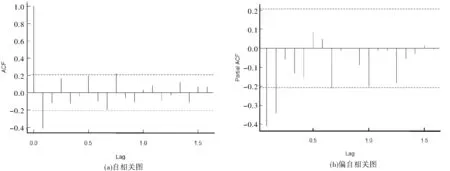
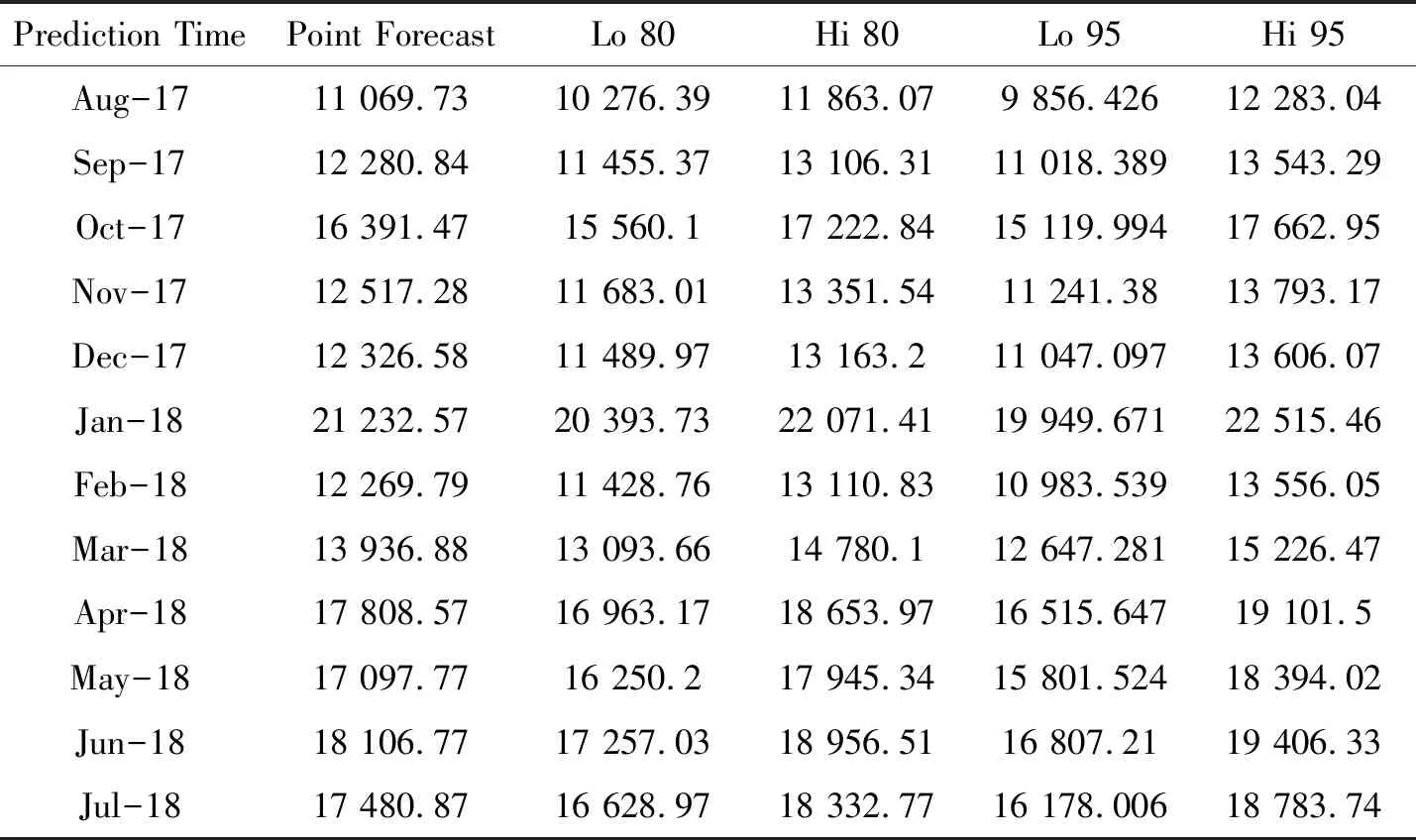
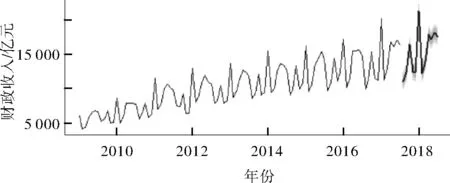
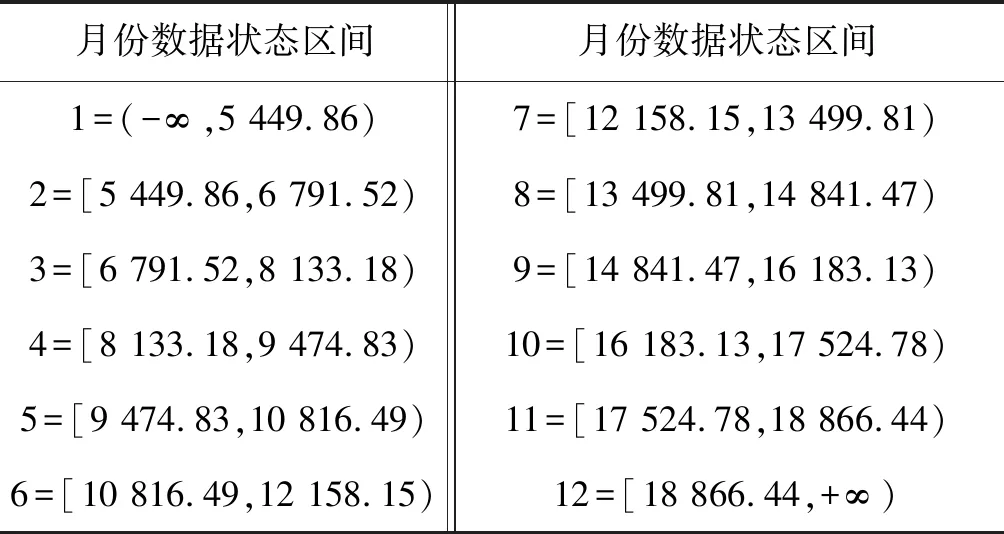
设{X(t),t∈T}为一随机过程,ti∈T,i=1,2,…,n且t1 P{X(tn) 则称{X(t),t∈T}具有马氏性或无后效性,并称{X(t),t∈T}为马尔科夫过程. 若上述马尔科夫过程的状态空间S为R中的可列集,时间参数集T为可列离散集,则称{X(t),t∈T}为离散参数马氏链. P{Xm+1=j|Xm=i,}≡P{X1=j|X0=i}≡Pij(m,1)≡Pij. 则称马氏链具有“平稳性”或“齐次性”,Pij表示由状态i经过一步转移到状态j的概率,它具有下列性质: 以pij为元素的矩阵P=(pij)称为状态转移概率矩阵,其形式为: 设事物有n个互不相容的状态,其初始分布为I(0)=[i(0)1i(0)2…i(0)n],式中i(0)t(t=1,2,…,n)表示在时刻0处于状态t的概率,若经过k步转移后处于状态t的概率为i(k)t,由C-K方程可得 i(k+1)t=∑i(k)t·pij(t=1,2,…,n), 简记为 I(1)=I(0)·P,I(2)=I(1)·P=I(0)·P2, …I(k+1)=I(k)·P=…=I(0)·P(k+1). 这就是马氏链预测模型.可见对于马氏链,它处于任意时刻的概率分布由上一步状态转移概率所决定. 笔者在中国知网数据库获取2009年1月—2018年7月的中国财政收入月度数据,通过R语言对2009年1月—2017年7月数据进行分析[3-8],保留2017年8月—2018年7月的数据,与将要预测的数据进行对比.图1为中国财政收入月度数据的时序图. 图1 2009年1月—2017年7月全国财政收入时序图 利用Eviews对中国财政收入月度数据进行ADF平稳性检验,3个模型的t-Statistic大于3个测试临界值且P>α=0.05,则说明拒绝原假设,中国财政收入月度数据是非平稳的,需要进行差分运算. 图2为确定性因素分解图,其中图(a)为原始数据时序图、图(b)为趋势图、图(c)为周期性趋势图、图(d)为残差序列图,从图(b)可以看出中国财政收入序列蕴含一个近似线性的递增趋势,所以对该序列进行一阶差分运算.进行差分运算后可以更好地提取周期信息.对于蕴含固定周期的序列进行步长等于周期长度的差分运算,可以更好地提取所分析的中国财政收入月度数据,可得周期12,所以进行1阶12步差分后可得时序图3. 图2 因素分解拟合综合输出图 图3 差分后中国财政收入序列时序图 图3显示序列在均值附近比较稳定地波动,还需要借助ADF检验进一步验证差分后序列的平稳性.利用Eviews对中国财政收入月度数据进行ADF平稳性检验,3个模型的t-Statistic小于3个测试临界值且P<α=0.05,说明接受原假设,中国财政收入月度数据是平稳的,可以进行白噪声检验.白噪声检验结果显示,LB统计量p-value=0.00,(P<0.05),所以我们可以认定全国财政收入序列属于非白噪声序列,可以进行模型拟合. 图4为1阶12步差分的自相关图和偏自相关图,从图(a)可以看出,1阶12步差分的自相关图是拖尾的.从图(b)可以看出,1阶12步差分的偏自相关图是拖尾的.则得出结论建立ARMA模型,又因为观察值序列是非平稳的,所以建立ARIMA模型. 通过R语言对差分后的中国财政收入月度数据进行系统定阶,可得系统定阶模型ARIMA(1,1,1)(0,1,0)12,见表2. 图4 1阶12步差分后的自相关图和偏自相关图 表2 系统定阶模型系数 根据模型拟合输出结果,可以得到系统定阶模型ARIMA(1,1,1)(0,1,0)12的拟合模型为: 从残差白噪声检验结果中可以看出,在延迟6阶和延迟12阶的检验p值分别为0.61、0.08,在显著性水平α为0.05的条件下,p值大于显著性水平,所以接受原假设,可以认定系统定阶模型ARIMA(1,1,1)(0,1,0)12提取的数据信息较为充分,该模型的拟合效果较为理想. 由表3系统定阶模型预测结果可知,利用系统定阶模型ARIMA(1,1,1)(0,1,0)12对2009年1月—2017年7月的中国财政收入进行预测,得出预测结果Point Forecast列. 利用R语言建立模型,对未来2017年8月—2018年7月的中国财政收入数据进行预测后,通过R语言拟合出系统定阶模型ARIMA(1,1,1)(0,1,0)12的预测图(图5),并根据保留的真实值建立预测结果对比表(表4). 表3 系统定阶模型预测结果 图5 系统定阶模型ARIMA(1,1,1)(0,1,0)12预测图 表4 系统定阶模型预测结果对比 表4是对2017年8月—2018年7月的预测值与真实值做差值得到相对误差,对相对误差取绝对值并与真实值做除,计算可得1年的预测结果的平均误差为4.75%,相对误差在5%以内,所以认为模型的预测效果较好. 2009年1月—2018年7月中国财政收入月份之间起伏明显[9-13],且一直呈现增长趋势.各月份之间差异明显,可以划分状态区间,把月份间的起伏变化转化成状态区间的转化.可以将中国财政收入月份数据划分为12个状态区间(表5). 表5 财政收入12个状态区间 由于数据呈现上升趋势,而基于马氏链的预测方法是基于已知状态的概率预测,对于预测数据将会呈现更高的状态,会导致预测结果不准确.因此对各个状态做差,对差值进行基于马氏链的预测.由此可以得到状态区间及相邻状态区间的差值. 对状态区间差值进行基于马氏链的预测,状态区间之间的变换转化为相邻状态区间差值之间的变换.再将状态区间差值分成新的状态区间[abcdef],可得表6. 表6 6个差值状态区间 利用MATLAB对数据状态区间划分状态,可以将状态区间的差值划分为6个状态区间[abcdef],根据各个状态的转移概率可得转移矩阵: 根据所建立的马氏链模型pk+1=p0·Pk+1,对未来时刻的状态分布进行运算[5-6]:将2018年1月的数据设为p0,p0=[0 0 0 0 0 1]为0时刻的状态向量,预测2018年2月—2018年7月的数据,分别求出(p1,p2,p3,p4,p5,p6). p1=p0·P⟹p1=[0.666 7 0.333 3 0 0 0 0],p2=p0·P2⟹p2=[0 0 0 0.833 3 0.166 7 0],p3=p0·P3⟹p3=[0.048 5 0.063 6 0.193 9 0.245 5 0.345 2 0.133 3],p4=p0·P4⟹p4=[0.127 4 0.154 7 0.175 4 0.374 2 0.129 1 0.039 3],p5=p0·P5⟹p5=[0.052 9 0.090 5 0.126 3 0.492 1 0.178 3 0.059 9],p6=p0·P6⟹p6=[0.075 8 0.100 1 0.157 6 0.381 1 0.206 6 0.078 7]. 由MATLAB求得预测结果(p1,p2,p3,p4,p5,p6)后,分别找出状态向量中概率最大所对应的状态区间,并与真实值状态区间进行对比. p1=[0.666 7 0.333 3 0 0 0 0]可得最大概率66.67%在a区间且与真实值在同一区间;p2=[0 0 0 0.833 3 0.166 7 0]可得最大概率83.33%在c区间且与真实值在同一区间;p3=[0.048 5 0.063 6 0.193 9 0.245 5 0.345 2 0.133 3]可得最大概率34.52%在e区间且与真实值在同一区间;p4=[0.127 4 0.154 7 0.175 4 0.374 2 0.129 1 0.039 3]可得最大概率37.42%在d区间且与真实值在同一区间;p5=[0.052 9 0.090 5 0.126 3 0.492 1 0.178 3 0.059 9]可得最大概率49.24%在d区间且与真实值在同一区间;p6=[0.075 8 0.100 1 0.157 6 0.381 1 0.206 6 0.078 7]可得最大概率38.11%在d区间,真实值在c区间. 由上述可得p1,p2,p3,p4,p5预测的结果与真实值相符合,从第6个数据开始预测出现较大偏差.马氏链模型预测的结果与转移概率矩阵有较大的关系,转移时根据相邻的观测数据状态区间转移的概率得到结果.通过马氏链模型可以得到中国财政收入的大致走向与所在范围. 根据10年中国财政收入月度数据的分析可知,我国财政收入总体呈现出递增趋势,但是一年内月度之间财政收入波动越来越大,导致中国财政收入预测难度越来越大.笔者利用系统定阶模型ARIMA对2017年8月—2018年7月的中国财政收入数据进行预测并进行相应分析,利用马氏链模型对2018年2月—2018年7月的中国财政收入数据进行预测并进行相应分析. 图6为系统定阶的拟合效果图,从图中可以看出,模型与原始数据拟合的效果较好,都在两倍标准差范围内;预测的1年的中国财政的趋势与往年的趋势是一样的,直观上可以认为预测结果较好. 图6 系统定阶模型拟合效果 对ARIMA模型和马氏链模型预测的结果进行分析:ARIMA模型的优点是比较容易建立,相比较马氏链模型可以作长期预测;缺点是时间序列数据必须是平稳的,或者通过差分后是平稳的. 马氏链模型的优点:模型简单,无后效性;缺点:由于马氏链具有平稳性,在长期预测中预测值会趋于一致,所以只适用于短期预测,具有局限性. 系统定阶模型ARIMA(1,1,1)(0,1,0)12的平均相对误差为4.75%.马氏链模型预测的结果是状态区间,前5个预测结果都在真实值所在的区间,第6个预测结果出现较大偏差状态区间.马氏链模型适用于短期预测,预测的越多越不准确,马氏链模型预测的结果是一个范围区间,预测结果没有ARIMA模型预测的准确度高.
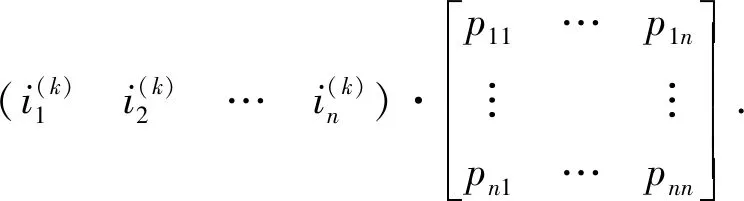
2 实证分析
2.1 ARIMA模型的建立与分析



2.2 马氏链模型的建立与分析


3 结论


