基于负载观测器的PMSM分数阶滑模位置控制

白雪宁，杨向宇，赵世伟

(华南理工大学 电力学院，广东 广州 510641)

0 引言

近两年，永磁同步电机(permanent magnet synchronous motor，PMSM)被广泛应用于各类位置控制系统。传统的系统广泛采用PID控制器，但在日益复杂的工况下难以保证系统的性能。文献[1]在传统PID三闭环串级控制结构基础上，引入负载观测器，实现系统位置无差跟踪。文献[2]将反步控制与非奇异终端滑模控制相结合，并使用终端滑模负载观测器，有效实现系统位置的渐近跟踪。文献[3]研究了变切换增益的滑模控制器与降阶负载观测器，使系统具有良好的动态性能以及鲁棒性。文献[4]采用无源性控制算法，提高系统稳定性的同时使系统具有良好的跟踪性及抗扰性。文献[5]研究了基于细菌觅食优化算法的模糊控制，有效提高了系统的快速性和准确性。

针对PMSM位置控制系统，本文采用分数阶微积分，设计了分数阶滑模控制算法(fractional order SMC，FOSMC)。针对电机运行时的负载扰动，设计了降阶Luenberger负载观测器。最后使用Matlab/Simulink对本文设计的控制器与传统PID控制器以及整数阶滑模控制器(SMC)进行了仿真，并对仿真结果进行了分析和比较。

1 PMSM数学模型

本文研究PMSM转子永磁体为表贴结构，定子绕组为Y型联接。因此d、q轴绕组电感相等，即Ld=Lq；忽略定子电枢反应、磁路饱和及铁耗，通过恒幅值dq0变换，得到PMSM在dq坐标系中的数学模型。

定子电压方程如下所示：

(1)

本文采用id=0的控制策略，电磁转矩方程如下：

Te=1.5ktiq

(2)

机械运动方程如下所示：

(3)

式中：id、ud，iq、uq分别为定子绕组d轴与q轴的电流和电压；Rs为定子绕组电阻；ψf为转子永磁体磁链；np为电机极对数；ωe为电机电角速度；kt为电机转矩系数；J为电机转子转动惯量；TL为负载转矩；B为电机黏滞系数；θe为转子电角度。

2 分数阶滑模控制器设计

2.1 分数阶微积分

根据分数阶系统随时间平缓衰减的特性[6-8]，在SMC的基础上引入分数阶微积分，构造分数阶滑模面。

首先对分数阶微积分数学基础作简要阐述。由于Caputo定义下的分数阶微分方程与整数阶微分方程有相同的初始条件，具有明确的物理意义，在工程领域中应用最为广泛，故采用Caputo定义。设函数g(t)为定义在区间[a,b]上的m阶导数可积的函数，则Caputo分数阶微积分统一定义如式(4)所示。

(4)

将上式做拉氏变换如式(5)所示。

(5)

式中g(k)(0)为系统初始状态k阶导数。

为便于本节的分数与整数阶微分运算，定义微分算子如下 ：

(6)

式中：C表示被微(积)分函数定义域，λ∈Q。

实现分数阶微积分有多种算法，本文采用Oustaloup有理逼近算法[6]，通过窄带宽滤波器级联而成。假定选择拟合频率段为[ωl,ωh]，则可以构造出连续窄带宽滤波器传递函数如下式：

(7)

分数阶微积分比整数阶微积分具有更多的自由度[6-11]，通过合理选择分数阶次α，可获得更好的控制效果。

2.2 滑模控制器设计

(8)

令s=0，所得方程表示分数阶线性定常系统。根据分数阶线性定常系统渐进稳定的充要条件[10-12]：当c1>0时，若式(9)成立，则系统渐近稳定。

(9)

式中arg(·)为辐角主值。

为了削弱系统抖振，常用的方法是采用边界层引入饱和函数，一定程度会上降低系统的鲁棒性。因此为兼顾系统的鲁棒性，确保系统相轨迹接近平衡点时不会产生较大抖动，远离平衡点时增大等速趋近的权重，使系统能够更快地到达平衡点，本文改进趋近律如下：

(10)

式中：M>0；sgn(·)为符号函数。

对式(8)求一阶导，得

(11)

对式(11)求(1-α)阶导，并将式(2)、式(3)代入，得

(12)

式中Kt=1.5kt。

联立式(10)、式(12)，求得滑模控制率如下：

(13)

选取李亚普诺夫函数如下：

(14)

(15)

分析可知：

(16)

故本文设计的FOSMC是稳定的。

3 负载观测器设计

针对电机运行时负载扰动不确定，为使系统能够无差跟踪位置指令，本文设计了降阶Luenberger负载观测器，将观测值补偿给控制器。由于控制器采样周期较短，将负载扰动视为常量。选取状态变量x=[ωeTL]T，输入变量u=iq，输出变量为y=ωe。状态方程与输出方程如下：

(17)

(18)

式中G=[g1g2]T，为观测器状态反馈矩阵。

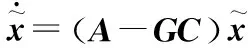
(19)

对式(19)作拉氏变换，可得观测误差方程的特征方程如下：

(20)

通过合理设计g1、g2，使特征方程具有负实部的根，则可保证观测器稳定收敛。

4 系统仿真与分析

为验证设计算法的有效性，利用Matlab/Simulink搭建系统仿真模型。图1为系统结构图。

图1 系统结构图

系统采用id=0的矢量控制，采用电流、位置双闭环控制方法。电流内环使用比例控制器，位置外环采用FOSMC。采用Luenberger负载观测器来观测外界负载扰动，将观测值作为补偿输入FOSMC。仿真使用的电机参数如表1所示。

表1 PMSM部分参数

为对比各控制器性能，仅改变位置环控制器(SMC的趋近律与FOSMC保持一致)，系统其余结构保持不变。

仿真时位置指令采用方波指令，周期1.5s，幅值90°，仿真时长6s。电机首先空载运行，在1.2s时突加0.5N·m负载作为外界负载扰动。为了更接近实际系统，电流控制器输出限幅。

图2 位置响应波形

图3 控制器电流指令与实际电流波形

如图2(b)，当电机空载运行时，FOSMC系统与SMC与PID系统相比，调节时间最短，且几乎无超调；系统在指令位置稳定时，无稳态误差。

图4 负载观测器观测波形

如图2(c)，当给电机突加负载时，位置均会受到扰动，FOSMC系统受扰动影响最小且最快恢复无差跟踪，动态性能略优于SMC系统以及PID系统。

对比图3(a)、图3(b)、图3(c)的局部放大部分，可以看出，FOSMC系统的控制指令较SMC系统与PID系统的动态过程更加平缓，有利于转矩输出更加平缓。

从仿真结果中可看出，在负载转矩产生扰动后，FOSMC系统相比较于SMC系统与PID系统表现出更好的鲁棒性，同时其动态性能也优于SMC系统与PID系统。

5 结语

综上所述，本文针对PMSM位置控制系统构造了分数阶滑模控制器并针对外部负载扰动的不确定性，设计了降阶Luenberger负载观测器。最后使用Matlab/Simulink搭建系统仿真模型，进行了算法验证。将仿真结果分别与采用整数阶滑模控制器与传统PID控制器的系统进行对比可知，本文设计的基于负载观测器的PMSM分数阶滑模位置控制系统具有调节时间短、无超调、无稳态误差，对外部负载扰动具有较强鲁棒性等优点，在位置伺服控制领域有较好的应用前景。