基于质量流模型的关联多工序制造过程加工质量研究

王菲，陈明

(1. 西安工程大学 计算机科学学院，陕西 西安 710600; 2. 湖南云箭集团有限公司，湖南 长沙 410000)

0 引言

在多工序制造系统中，制造过程质量控制的研究是当前质量管理研究的一个热点。制造过程中最基本的单元是工序，对各工序的质量实施管理是提高产品设计质量的有力保证。

对于多工序制造过程的研究主要分为两类：一是考虑过程相关性而建立的多工序误差传递状态空间模型，可用于统计过程控制或全面质量管理[1-2]；另一类是建立加工过程模型，以研究制造系统设计对产品质量的影响[3-4]。KIM等[5]采用产品的合格率来预测系统的加工质量； WANG等[6]研究了质量的非单调性，也就是说，质量性能不会随制造系统某一参数的变化而单调变化。张伟[7]等根据多指标分析生产工序，应用Witness仿真软件，并结实例进行研究，结果表明该方法可以更加准确地找出影响生产过程质量的因素。但是，基于这些模型的研究前提是假设工序间是独立存在的，是不相互影响、不相互关联的，即没有考虑工序间质量误差的传递，使得模型的适用范围受到限制。JU等[8-9]以转移概率为基础建立了三状态质量流模型，其三状态涉及到 “合格”、“修复过合格”和“不合格”3种状态，但是实际生产中要在每一道工序后对产品加工状态质量进行检查再进行缺陷修理，极大地增加了成本并降低了生产效率，使模型受到限制。

通过上述分析，本文在权衡目前工序状态和上道工序产品质量的基础上，从工序之间关联性的角度研究了机械产品工件制造过程特性在工序间的相关性和变化关系，并推论出最终工件加工过程的质量模型，从制造过程参数的角度提出制造系统加工质量的改进建议。

1 关联多工序制造过程的质量流模型建模

1.1 模型假设

本文采取质量流模型对产品加工过程建立模型，构建模型的前提假设如下：

1)当设备处于无故障运行状态时，生产的产品质量状态合格与不合格的情况是随机分布的。制造过程的相邻工序间存在质量传递，经过第i道工序的产品质量不仅受到自身工序的影响，而且还受到上道工序产品质量的影响。

2) 以产品质量衡量工序的加工状态，在t时刻，若工序Mi生产的产品质量合格，则认为t时刻Mi处于gi(第i道工序产品质量为合格)状态；同理，若工序Mi生产的产品质量不合格，则认为t时刻Mi处于di(第i道工序产品质量为合格)状态。

3) 工序M1的加工状态不受下一道工序的生产状态的影响，即若t时刻M1处于gi状态，则在t+1时刻，它有η1(工序维持gi的概率)概率维持gi状态，有1-η1的概率转移到di状态；同理，如果t时刻M1处于di状态，则在t+1时刻，它有ν1的(工序维持di的概率)概率维持di状态由1-ν1率转移到gi状态。

4) 工序Mi(i≥2)在t时刻的上游产品质量取决于Mi-1在t-1时刻的状态，若Mi-1在t-1时刻处于状态gi-1，则Mi在t时刻的上游产品质量是合格的;同理，若Mi-1在t-1时刻处于状态di-1，则Mi在t时刻的上游产品质量是不合格的。

当上道工序产品质量合格时，若Mi在t时刻处于gi状态,则在t+1时刻由βi(第i道工序产品质量由合格转化为不合格的概率)的概率转移到di状态，有αi(第i道工序产品质量维持合格率)的概率维持gi状态；当上游产品质量不合格时，若Mi在t时刻处于di状态,则在t+1时刻由λi(第i道工序产品质量由不合格转化为合格的概率)的概率转移到gi状态，有δi(第i道工序产品质量维持不合格率)的概率维持di状态。

1.2 关联多工序的质量流加工模型

多工序加工系统中的产品加工过程质量传递具有很大的复杂性，除了在单个工序上的各种影响因素之外，相连工序之间存在复杂的相互联系，工序之间可能引入各种误差，导致产品的加工质量下降并随工序不断积累，因此，在加工过程中，相邻工序间质量的传递尤为重要。

在产品加工过程中，来料在经过某道工序后的质量可能会出现由合格变为不合格(质量损失)或由不合格变为合格(质量补偿)的现象。因此，每道工序加工后的产品质量与目前工序状态和上道工序产品质量都紧密相关。在文献[8-9]提出的模型基础上并综合当前设备状态和上道工序产品质量因素的影响，提出关联多工序制造系统的加工过程转移概率图如图1所示。

图1 关联多工序转移概率图

由图1可推导出关联多工序产品制造过程的质量流模型如下：

两道工序产品质量模型：

p(g1)=p(g0)α1+p(d0)λ1

(1)

p(d1)=p(g0)β1+p(d0)δ1

(2)

多道工序产品质量模型：

p(gk)=p(gk-1)αk+p(dk-1)λk

(3)

p(dk)=p(gk-1)βk+p(dk-1)δk

(4)

2 案例分析

2.1 案例描述

以某公司高压开关操动机构智能车间生产零部件工作缸的生产过程来验证多工序质量流模型的有效性。工作缸的生产过程主要包括粗车、热处理、精车、去毛刺、阳极氧化和研磨清洗等，加工内容如表1所示，工作缸的剖面图如图2所示(左为小端，右为大端)。

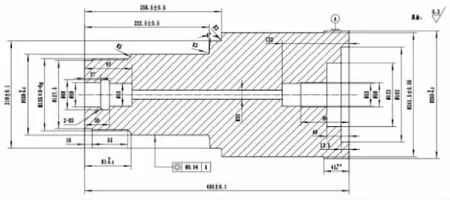
图2 工作缸剖面图(示意图)

表1 工作缸加工过程

工序工序名称工序内容1粗车按具体尺寸以探伤面作为零件螺纹端进行加工,切除大部分余量2热处理对零件进行调质和表面渗氮处理3半精车对零件进行半精加工,使尺寸大小接近零件规定尺寸4精车把零件加工到图样规定要求5去毛刺去各相贯孔毛刺,对螺丝孔深度不够进行修理6阳极氧化硬质阳极氧化50 μm,除ϕ35.03±0.01、ϕ55.075±0.01孔外其余孔7研磨清洗超声波旋转清洗:ϕ45+0.03-0.01(小端)、ϕ45+0.03-0.01(大端)

本文提出了基于各工序设备状态和上道工序工件质量的关联多工序加工过程质量模型，实验中采用如下方法获取参数：1)在无故障运作阶段，收集经过各道工序加工后的工件质量状况，并以零部件质量“合格”和“不合格”进行记录和区分。2)对某道工序的加工工序Mi分别在上游零部件质量合格、不合格的情况下，统计以下情况的占比：①上道工序加工的工件i-1质量合格且此工件质量也合格；②上道工序加工的工件i-1质量合格而此工件质量不合格；③上道工序加工的工件i-1质量不合格而此工件质量合格；④上道工序加工的工件i-1质量不合格且此工件质量也不合格。

对于工序Mi(i≥2)，在上道工序工件质量合格时，情况①、②所占比例对应转移概率αi、λi，在上道工序工件质量不合格时，情况③、④所占比例对应转移概率βi、δi；而对于工序M1，其上道工序工件质量经过检验都合格，因此情况①、②所占比例对应转移概率ηi、νi。

2.2 生产瓶颈识别

通过收集工作缸加工过程的各个工序加工后工件质量参数的测试数据，对每道工序进行了5组测试，每组包括1000个工作缸零部件，统计计算所得实际各设备对应工序的参数如表2所示。将表2的数据带入工序加工过程的质量流模型式(3)中，进行计算得出经过各工序后的工作缸合格率如图3所示。

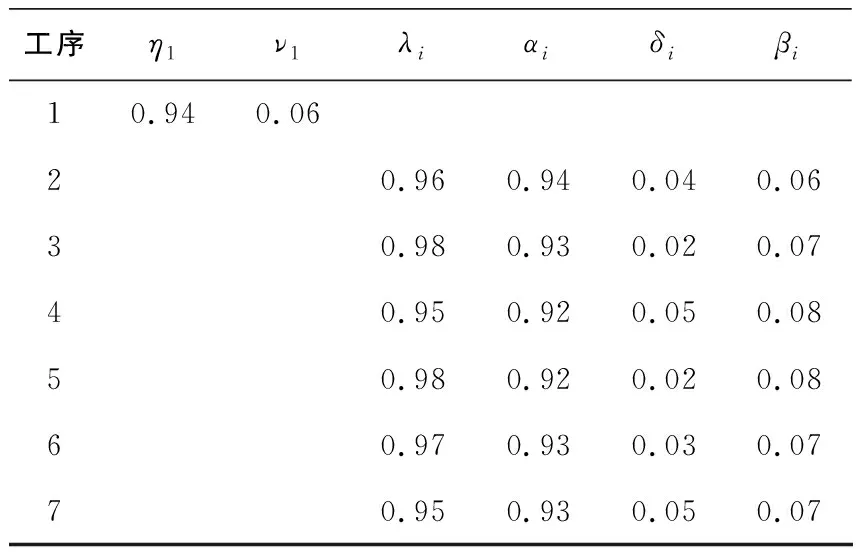
表2 制造系统的设备对应的工序参数

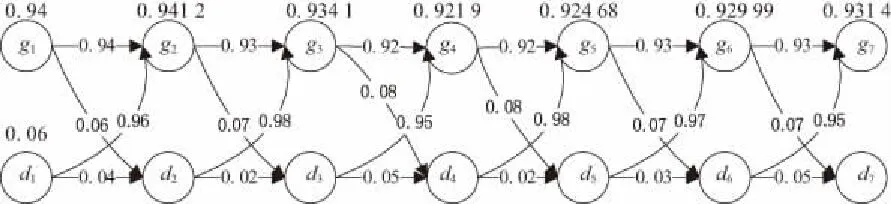
图3 工作缸加工过程转移概率图

根据建立的质量流模型所得工作缸经过该制造过程的各道工序后工件加工质量合格率变化趋势如图4所示。

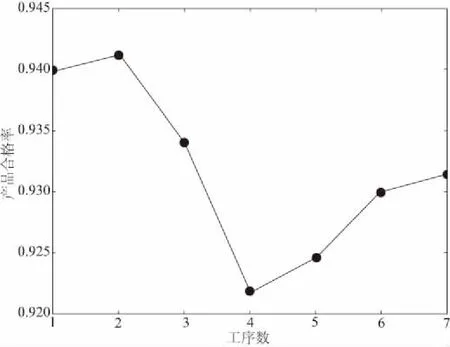
图4 产品加工过程合格率变化图

经过第i道工序后，工作缸加工合格变化量Δp(gi+1)(此道加工工序的零件合格率与前一道工序加工合格率的差值)为：

ΔP(gi+1)=P(gi+1)-P(gi)

由此可计算出：

ΔP(g2)=0.00120,ΔP(g3)=-0.00710,

ΔP(g4)=-0.01220,ΔP(g5)=0.00278,

ΔP(g6)=0.00531,ΔP(g7)=0.00141。

由图4和Δp(gi+1)得出，从第4道工序后，工作缸加工合格率出现了较大幅度下降，因此，系统中最需得到质量提升的工序为工序4。将表2中的参数带入建立的质量流模型中，通过模型计算得到该加工制造过程的合格率为0.9314，历史数据中实际加工工件合格率为0.9349，相对误差为0.35%，证明此模型可以应用于该实际加工过程。

第4道工序的相关参数有λ4、α4、δ4和β4，在当前真实值的基础上，分别对这些变量进行单因素变化，观察在第4道工序时零部件加工合格率的变化，由图5可见α4的变化对该制造过程合格率影响最大，在变化相同值的情况下，提高α4的值能够最大程度地提高该制造过程的合格率。

图5 M4的参数与产品加工合格率的变化关系

通过该模型找到了工作缸加工制造过程的质量瓶颈工序和质量瓶颈加工参数，并得出了加工参数对零部件合格率的影响规律。在该加工过程中，需要整改的是第4道工序，其瓶颈参数为α4。因此，在加工前5M1E(操作人员、加工设备、工件材料、工艺方法、现场环境和测量方式)是符合加工标准要求的前提下，对第4道工序相关的工艺系统(机床、刀具、夹具、工件和切削液)在加工过程中的受力变形、受热变形等原因进行主要排查，使第4道工序不再是加工质量的瓶颈工序，从而提高产品的合格率。

3 结语

生产过程管理问题是工业生产的重点，在生产过程中，各工序间加工质量的传递会影响最终产品的质量，从而影响企业的经济效益，制约企业的生产发展，所以在生产过程中，及时找出生产瓶颈十分重要。本文对制造系统的加工过程进行分析，综合权衡上道工序产品质量和目前工序状态两个影响因素，构建了生产线传递的关联多工序制造过程的质量流模型，强调加工质量传递对产品质量的影响，结合智能车间的工件工作缸加工过程案例，找出了瓶颈工序及瓶颈参数，验证了模型的实用性，并给出了加工质量改进建议。