基于时空聚类的在制品流转状态分析
王益聪,郭宇,黄少华,张蓉,冯上海
(1. 南京航空航天大学 机电学院,江苏 南京 210016;2. 中航工业江西洪都航空工业集团有限公司,江西 南昌 330024)
0 引言
离散制造车间中,制造过程根据产品加工工艺分为多道工序,在制品需要在多个工位间流转[1]。通过车间实时定位系统,能够有效获取在制品实时位置信息。对在制品位置数据的挖掘能够提取在制品在车间流转的频繁时空路径,通过计算在制品流转过程中实时数据和挖掘的频繁路径的偏差,判断在制品流转状态是否发生异常。
随着无线通信技术的发展,室内定位技术在车间的应用越来越成熟。文献[2]提出了一种新的基于射频识别(radio frequency identification,RFID)和WiFi技术的实时定位系统,实现仓库的自动化、数字化和智能化管理,大大提高了仓库运行效率,降低了仓库管理成本;文献[3]研究了实时定位技术对生产调度的影响,工艺员可以通过定位系统提供的位置数据流实时跟踪在制品的生产状态,进而掌握并合理安排每个工位的加工时间,实现生产资源的动态调度和规划;文献[4]将基于RFID技术的实时定位系统应用到半导体制造车间中,研究了在车间生产流程中通过实时定位技术获取的不同生产过程对象位置信息的价值,表明实时定位的应用提供了更好的可视化水平以及更加高效的生产效率。现代观测技术、计算机网络和地理信息系统的快速发展,生成大量时空数据,对时空数据分析方法的研究日益增多。文献[5]提出了基于时空对象的聚类方法,有助于全面分析时空对象空间位置、属性特征及其变化特点,为多粒度时空对象分析提供思路;文献[6]利用个体出行的GPS轨迹数据,在DBSCAN的基础上提出一种新的时空聚类算法,以时空邻近条件定义簇间距离,识别GPS轨迹中的停驻点;文献[7]对船载AIS数据展开时空聚类分析,在DBSCAN算法基础上提出船载AIS数据时空聚类算法,发现隐含的时空模式,为船舶交通管理提供了一种新途径。
通过分析发现,实时定位在车间主要应用于制造要素的可视化跟踪和监控,而缺少对位置数据和制造过程之间潜在关系的挖掘。本文以室内定位技术为基础,有效获取离散制造车间在制品实时位置数据,实时计算车间现场在制品流转状态偏差,及时发现异常,为制造过程动态优化提供依据。
1 在制品流转状态分析
在制品的时空数据是定位系统产生的一连串包含时空信息的位置点组成的集合P={p1,p2,…,pn},每个点包含时空坐标pi=(xi,yi,ti)。通过对在制品时空数据的聚类分析,可以发现一些隐含的流转模式和规律,获取在制品流转过程时空模型,然后通过计算在制品实时位置数据与聚类结果的相似度,来分析在制品流转状态,其中在制品流转状态集合为{正常,预警,异常}。技术路线如图1所示。
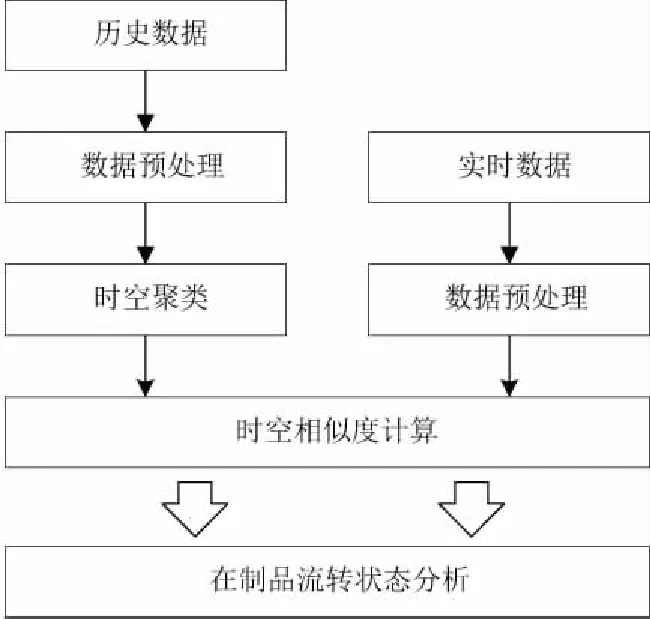
图1 在制品流转状态分析技术路线
2 在制品流转数据时空聚类方法
2.1 在制品时空轨迹定义
在制品时空轨迹是在空间维度和时间维度上的运动轨迹,表达了在制品空间位置随时间的变化。时空轨迹由一系列时空记录组成,每条记录包括在制品的位置信息和记录时间。
实时定位系统产生的位置数据记录主要包括移动目标o、位置数据(x,y)和时间t。对于在制品oi,将其时空轨迹定义为Ti={(x1,y1,t1),(x2,y2,t2),…,(xn,yn,tn)},如图2所示。

图2 在制品时空轨迹
在制品时空轨迹包含了丰富的生产过程信息。仅考虑空间轨迹,可以获取在制品在车间哪些区域、工位间流转,即在制品工艺路线;结合时间信息,能够反映在制品在何时到达哪个工位,加工了多长时间等。
2.2 基于网格的在制品时空轨迹聚类算法
网格聚类算法的原理是将数据空间划分为网格单元,将数据集映射到网格单元中。这种方法的优点是处理速度很快,其处理时间独立于数据对象数目,只与划分的单元数目有关,是空间数据处理中常用的将数据离散化的方法[8]。针对离散制造车间位置数据的特点,采用网格聚类算法对在制品时空数据进行处理。
传统意义上的轨迹通过位置点序列来表达,这给存储和处理带来了困难,而网格聚类将轨迹的位置点映射到划分的网格单元中,极大减小了存储空间和处理的复杂度。如图3(a)所示,轨迹由一系列带有x,y坐标的特征点表达,即{(x1,y1),(x2,y2),…,(xn,yn)}。而在网格表达形式中,同一条轨迹表达如图3(b)所示,将轨迹按经过的网格单元表达,用网格单元的行列索引号来表示,即{(3,1),(3,2),(3,3),…,(6,8),(6,9)}。网格表达形式具有数据结构简单、定位存取性能好的特点。时空轨迹则由三维空间网格单元序列来表示。

图3 轨迹的两种表达形式
网格聚类算法核心思想如下:将数据集的每一个维度划分成网格单元,扫描所有网格,如果一个网格单元中包含的数据点数超过了给定的密度阈值,则称该单元是密集的[9]。这些连通的密集单元的最大集合就是簇的定义。算法的相关定义如下:

定义2(网格单元密度) 当1条数据pi∈Gj,即(xi,yi,ti)∈Gj,则称该条数据属于网格单元Gj。网格单元Gj中包含的数据总数称为Gj的网格单元密度density(j)。
定义3(密集网格单元、稀疏网格单元) 设置密度阈值τ,对于1个网格单元Gj,当density(j)>τ时,称该网格单元为密集网格单元,否则为稀疏网格单元。
(1)
定义6(簇) 数据空间中最大密度相连的网格单元的集合称为1个簇Ci。
2.3 算法流程
网格聚类算法主要是对车间采集的在制品历史数据进行分析处理,得到的结果作为在制品流转状态实时分析的依据。具体流程如图4所示。

图4 算法流程图
算法流程详细步骤如下:
步骤1:根据车间布局和生产过程的特点,确定数据空间每一维的网格划分参数λx,λy,λt,初始化网格单元状态。
步骤2:读取数据,更新网格单元状态。
步骤3:根据网格单元密度判断是否为密集网格单元,若是密集网格单元,则跳至步骤4,否则跳至步骤7。
步骤4:将密集网格单元加入相应的簇中。
步骤5:判断密集网格单元的邻接网格是否密集,若是,则跳至步骤4,若否,跳至步骤6。
步骤6:判断邻接单元是否遍历完成,若否,跳至步骤5,若遍历完成则生成1个簇。
步骤7:判断网格单元是否遍历完成,遍历完成则输出簇队列,否则跳至步骤3。
算法输出的结果是一系列簇C1,C2,…,Cn,每个簇为1个网格序列,对应在制品的时空轨迹。
3 基于改进Hausdorff距离的时空相似度计算
3.1 改进Hausdorff距离
在制品流转状态异常检测是对制造过程中实时采集的数据进行处理,通过计算实时流转轨迹和聚类结果的相似度来分析在制品的流转状态。时空轨迹相似度计算主要依赖于轨迹之间距离的定义以及轨迹之间的匹配程度。Hausdorff距离是描述两点集之间相似程度的一种度量方法。给定两点集A={a1,a2,…},B={b1,b2,…},两个点集之间的Hausdorff距离为:
H(A,B)=max[h(A,B),h(B,A)]
(2)
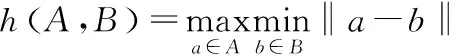
(3)
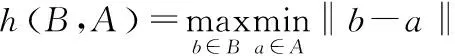
(4)
其中:‖a-b‖是点a和b之间的距离度量;H(A,B)称为双向Hausdorff距离;h(A,B)称为点集A到点集B的单向Hausdorff距离;h(B,A)称为点集B到点集A的单向Hausdorff距离。双向Hausdorff距离是2个单向Hausdorff距离中的较大者,它度量了2个点集之间的最大不匹配程度[10]。
又经过半个多小时的努力,虽然确诊是牙了,但却由于时间过长,息肉几乎已经把牙包住了,怎么也拿不出来,最终,段主任决定放弃手术。就在那一刹,我和老婆顿觉坠入了冰窖里。
传统的Hausdorff距离中‖a-b‖多采用欧式距离,而对于时空轨迹点之间的距离需要同时考虑时间和空间,因此给出时空距离的定义。
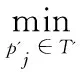
(5)
(6)
结合时间距离和空间距离,定义时空距离为:
DST(pi,T')=DS(pi,T')×DT(pi,T')
(7)
在制品时空轨迹相似度的计算主要是计算实时轨迹和聚类结果之间的Hausdorff距离,因此只计算实时数据到聚类结果的单向Hausdorff距离,最后改进的Hausdorff距离为:
(8)
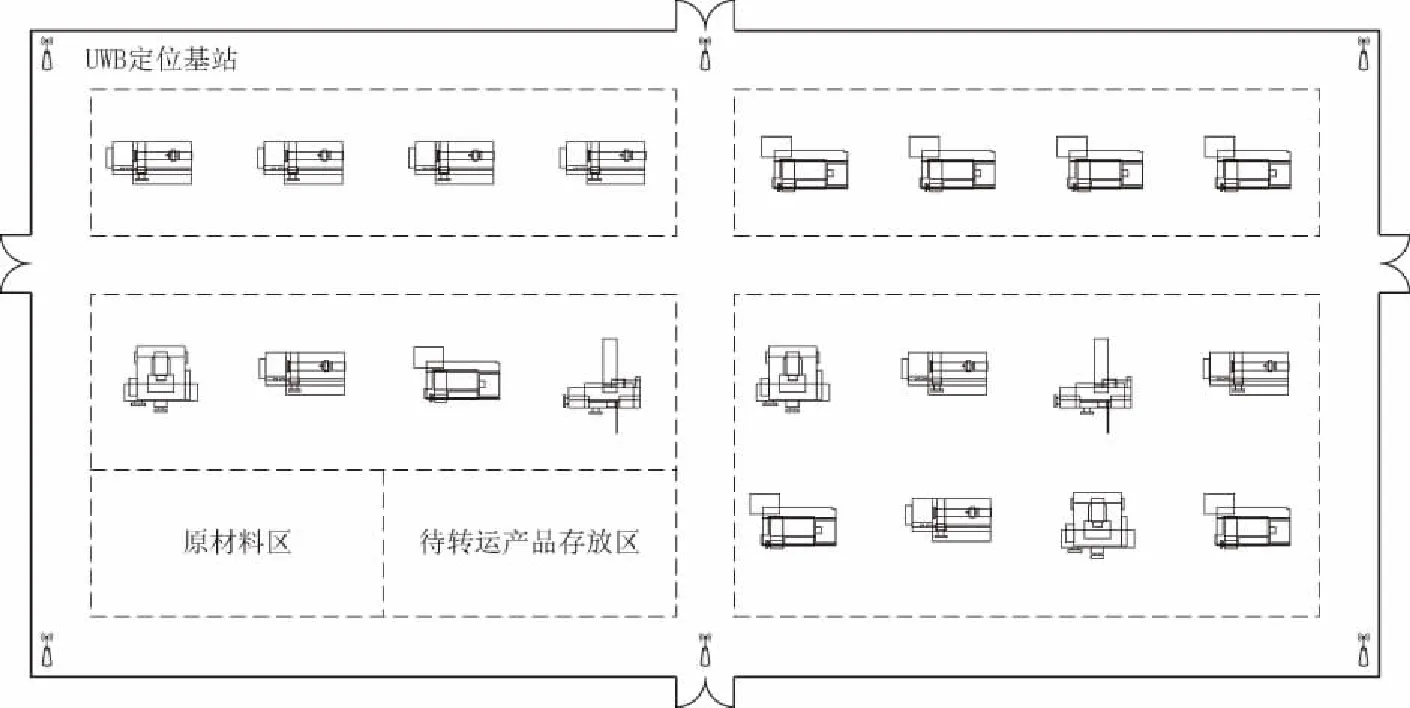
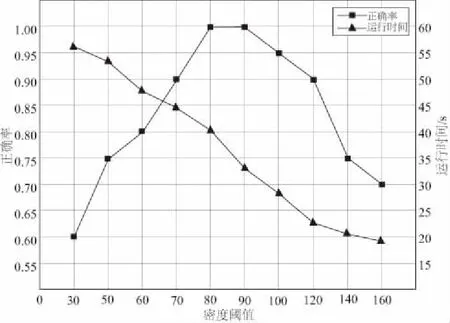
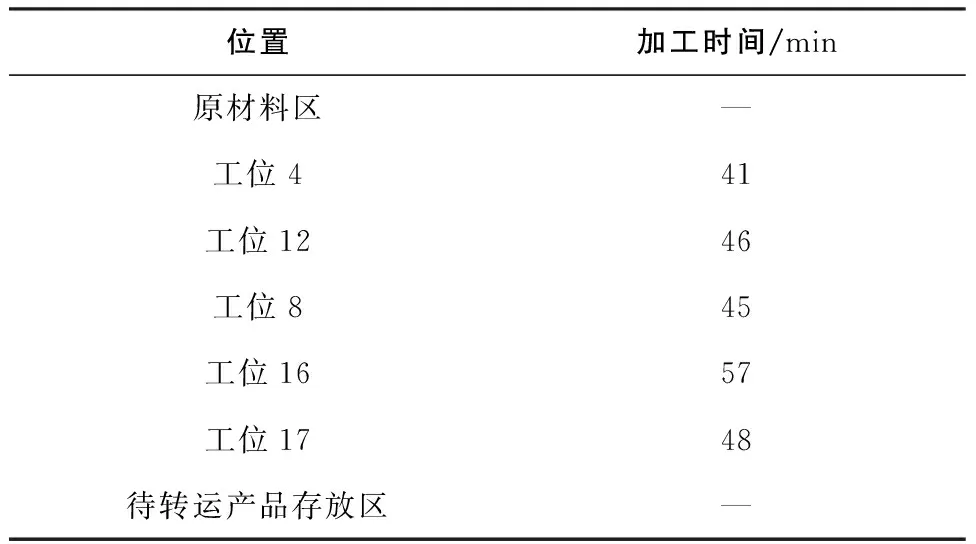
由上面的距离定义可知,改进的Hausdorff距离取值范围在0~1之间,且Hm(T,T')越小,轨迹T和T'的时空相似度越高。Hm(T,T')≤H1时,在制品流转为正常状态;H1 已有的Hausdorff距离计算相似度考察的是两个无序的集合,而时空轨迹数据是有序的。因此采用基于时间约束的时空相似度计算方法。 图5 滑动时间窗模式 以某机加车间为例,车间部署了UWB室内定位系统,通过定位标签实时获取在制品等制造要素的位置信息,在Intellij IDEA平台进行了实验。车间尺寸为92m×44m,共有1个原材料区、1个待转运产品存放区和20个加工工位。原材料区和待转运产品存放区尺寸约为20m×10m,各工位尺寸约为10m×10m,其中每个工位包含缓冲区(约10m×2m)和加工区(约10m×8m)。物料从原材料区粘贴定位标签,并配送到各加工工位,加工完成的产品运送到待转运产品存放区。车间布局如图6所示。 图6 车间布局 车间正常生产过程中采集到的每条位置数据包括:ID、采集时间和坐标信息,数据采集频率为4Hz。由于原始采集的数据中时间记录为绝对时间,无法直接对时间进行划分。在对原始数据进行聚类之前,先进行预处理:将在制品离开原材料区的时刻记为t0,则处理后的数据为(ID,x,y,t-t0)。 车间采用的UWB定位系统动态定位误差90%的情况下<30cm,约99%的情况下定位误差<60cm。同时考虑加工区、缓冲区和通道等区域的尺寸,避免同一网格跨越不同功能区域,设置车间空间网格划分粒度为0.5m×0.5m。为保证一定的实时性以及尽可能降低算法复杂度,设置时间维度网格步长λ=1min。网格聚类的关键参数密度阈值τ对聚类结果影响较大,实验结果表明,τ值偏大会导致本属于同一个簇的网格被分到两个簇,容易丢失在制品流转过程信息;τ值偏小会将不同簇的网格聚到一起,同时会受到异常数据和稀疏数据的影响,导致聚类结果失真,同时增加了算法的时间复杂度。对于不同的参数τ取值,算法的正确率和运行时间如图7所示。 图7 不同参数下算法正确率和运行时间 从图中可以看出,在密度阈值设置为80和90时,算法正确率为100%,而算法运行时间随着密度阈值的增大而减小。综合考虑算法正确率和运行时间,设置密度阈值τ=90,对在制品历史轨迹数据进行聚类。部分聚类结果如表1所示。 表1 算法结果 表中列出了在制品停留时间较长的网格,结合车间几何空间和语义空间,聚类结果可以解释为在制品的加工路线详细信息,如表2所示。 表2 在制品加工路线 在制品流转轨迹时空相似度计算过程中,设置时间间隔tgap=5min,即每5min更新一次相似度计算结果。根据车间布局以及在制品加工用时,取在制品流转状态变化临界值H1=0.19,H2=0.42。采用某在制品加工过程中采集的数据作为模拟实时数据输入,改进Hausdorff距离计算结果如图8所示。 图8 计算结果 从图中的计算结果可以发现,在制品流转状态在160min之前处于正常状态,165min时改进Hausdorff距离增大,进入预警状态,185min时进入异常状态,改进Hausdorff距离在200min开始趋于稳定。结合车间实际情况,工位16的机床在165min左右时发生故障,导致在制品在工位16的缓存区停留时间过长,同时,机床在195min左右恢复正常。由此证明了本文提出方法的有效性。 离散制造车间在制造过程中难免发生异常情况,如设备故障、物料配送异常、人员离岗等,一旦无法及时发现并处理车间生产异常,将直接影响车间制造活动的正常运行。而通过结合在制品的实时位置数据对在制品流转状态偏差进行实时分析,能够对在制品流转过程中发生的异常进行有效预警,有助于制造过程的正常运行。 实时定位技术在离散制造车间应用越来越广泛,因此产生了大量的位置数据。本文在离散制造车间实时位置数据的基础上对在制品流转状态分析展开研究。通过位置大数据处理方法建立在制品流转的时空轨迹模型,以此为依据,结合制造过程中实时位置数据计算流转状态偏差。最后,以某机加车间为例进行了验证,结果表明本文提出的方法可以有效分析在制品流转状态。3.2 基于时间约束的时空相似度计算

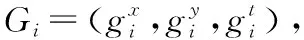
4 案例分析


5 结语

