试题情境创新的“三为本”
孙景波
(山东省淄博第十一中学,255086)
高考命题可粗略分为沿袭与创新两大类,从功能上看,这两类试题各有其作用.沿袭是一种对知识的继承,是强化基础的必由之路;创新是知识撞击的火花,是一个由量变到质变的过程.每年的高考都会推出一批新颖而又别致的创新试题,令高考精彩纷呈.从历年高考试题来看,创新题主要是指试题情境的创新,而且情境的创新也是“依纲据本”.
一、以教材为本
在选材立意上,以教材中核心概念、性质法则、定理公式和例题习题为载体,以考查基础知识和通性通法为主,以知识的交汇和应用为命题重点,检测学生对教材知识的理解与掌握程度.
例1(2018年浙江高考题)已知a1,a2,a3,a4成等比数列,且a1+a2+a3+a4=ln(a1+a2+a3).若a1>1,则( )
(A)a1 (B)a1>a3,a2 (C)a1 (D)a1>a3,a2>a4 解由结论lnx≤x-1,可知x≥lnx+1. 若公比q>0,则a1+a2+a3+a4>a1+a2+a3>ln(a1+a2+a3),不合题意;若公比q≤-1,则a1+a2+a3+a4=a1(1+q)(1+q2)≤0,但ln(a1+a2+a3)=ln[a1(1+q+q2)]>lna1>0,即a1+a2+a3+a4≤0 综上,a1>a1q2=a3,a2 评注通过函数不等式x≥lnx+1对题设不等式进行放缩,进而限制参数取值范围,是一个有效方法. 例2(2019年全国高考题)为了治疗某种疾病,研制了甲、乙两种新药,希望知道哪种新药更有效,为此进行动物试验.试验方案如下:每一轮选取两只白鼠对药效进行对比试验.对于两只白鼠,随机选一只施以甲药,另一只施以乙药.一轮的治疗结果得出后,再安排下一轮试验.当其中一种药治愈的白鼠比另一种药治愈的白鼠多4只时,就停止试验,并认为治愈只数多的药更有效.为了方便描述问题,约定:对于每轮试验,若施以甲药的白鼠治愈且施以乙药的白鼠未治愈则甲药得1分,乙药得-1分;若施以乙药的白鼠治愈且施以甲药的白鼠未治愈则乙药得1分,甲药得-1分;若都治愈或都未治愈则两种药均得0分.甲、乙两种药的治愈率分别记为α和β,一轮试验中甲药的得分记为X. (1)求X的分布列; (2)若甲药、乙药在试验开始时都赋予4分,pi(i=0,1,…,8)表示“甲药的累计得分为i时,最终认为甲药比乙药更有效”的概率,则p0=0,p8=1,pi=api-1+bpi+cpi+1(i=1,2,…,7),其中a=P(X=-1),b=P(X=0),c=P(X=1).假设α=0.5,β=0.8. (i)证明:{pi+1-pi}(i=0,1,2,…,7)为等比数列; (ii)求p4,并根据p4的值解释这种试验方案的合理性. 分析(1)首先确定X所有可能的取值,再来计算出每个取值对应的概率,从而可得分布列.(2)(i)求出a、b、c的取值,可得pi=0.4pi-1+0.5pi+0.1pi+1(i=1,2,…,7),再整理出符合等比数列定义的形式,问题得证;(ii)列出证得的等比数列的通项公式,采用累加的方式,结合p8和p0的值可求得p1,再次利用累加法可求出p4. 解(1)由题意,可知X所有可能的取值为-1、0、1. 于是,P(X=-1)=(1-α)β,P(X=0)=αβ+(1-α)(1-β),P(X=1)=α(1-β),得X的分布列如下: X-101 P(1-α)βαβ+(1-α)(1-β)α(1-β) (2)由(1)及α=0.5,β=0.8,得a=0.5×0.8=0.4,b=0.5×0.8+0.5×0.2=0.5,c=0.5×0.2=0.1. (i)由pi=0.4pi-1+0.5pi+0.1pi+1,整理可得5pi=4pi-1+pi+1,pi+1-pi=4(pi-pi-1),故{pi+1-pi}是以p1-p0为首项,4为公比的等比数列. (ii)由(i)知pi+1-pi=(p1-p0)·4i=p1·4i,故p8-p7=p1·47,p7-p6=p1·46,…,p1-p0=p1·40, 评注本题考查离散型随机变量分布列的求解、利用递推关系式证明等比数列、累加法求解数列通项公式和数列中的项的问题.本题综合性较强,要求学生能够熟练掌握数列通项求解、概率求解的相关知识,对学生分析和解决问题能力要求较高. 在设问方式上,以分步设问为主,采用递进式、并列式、类比式和开放式相结合的方式,表述贴近教材,让学生有似曾相似之感. 例3(2019年江苏高考题)定义首项为1且公比为正数的等比数列为“M-数列”. (1)已知等比数列{an}满足a2a4=a5,a3-4a2+4a1=0,求证:数列{an}为“M-数列”; (i) 求数列{bn}的通项公式; (ii) 设m为正整数,若存在“M-数列”{cn}(n∈N*),对任意正整数k,当k≤m时,都有ck≤bk≤ck+1成立,求m的最大值. 分析(1)由题意分别求得数列的首项和公比即可证得题中的结论.(2)第(i)问由题意利用递推关系式讨论可得数列{bn}是等差数列,据此即可确定其通项公式;第(ii)问由(i) 确定n的值,将原问题进行等价转化,构造函数,结合导函数研究函数的性质,即可求得m的最大值. 解(1)设{an}的公比为q,则a1≠0,q≠0. (ii) 由(i) 知bk=k(k∈N*).因为数列{cn}为“M-数列”,设公比为q,则c1=1,q>0.因为ck≤bk≤ck+1,所以qk-1≤k≤qk,其中k=1,2,3,…,m. 若m≥6,分别取k=3和6,得3≤q3,且q5≤6,从而q15≥243,且q15≤216,此时q不存在.因此,所求m的最大值小于6. 综上,所求m的最大值为5. 评注本题主要考查等差和等比数列的定义、通项公式、性质等基础知识,考查代数推理、转化与化归及综合运用数学知识探究与解决问题的能力. 在问题情境上,依托课本素材加工改造,将解决问题所需要的核心知识、思想方法、关键能力和数学文化内隐其中进行命题,反映数学的本质,有利于甄别学生的数学学科核心素养. 例4(2019年全国高考题)我国古代典籍《周易》用“卦”描述万物的变化.每一“重卦”由从下到上排列的6个爻组成,爻分为阳爻“——”和阴爻“——”,如图1就是一重卦.在所有重卦中随机取一重卦,则该重卦恰有3个阳爻的概率是( ) 分析本题主要考查利用两个计数原理与排列组合计算古典概型问题,渗透了传统文化、数学计算等数学素养,“重卦”中每一爻有两种情况,基本事件计算是住店问题,该重卦恰有3个阳爻是相同元素的排列问题,利用直接法即可计算. 评注对利用排列组合计算古典概型问题,首先要分析元素是否可重复,其次要分析是排列问题还是组合问题.本题是重复元素的排列问题,所以基本事件的计算是“住店”问题,满足条件事件的计算是相同元素的排列问题(即为排列组合综合问题). 例5(2015年湖北高考题)《九章算术》中,将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马,将四个面都为直角三角形的四面体称之为鳖臑.在如图2所示的阳马P-ABCD中,侧棱PD⊥底面ABCD,且PD=CD,点E是PC的中点,连结DE、BD、BE. (1)证明:DE⊥平面PBC,试判断四面体EBCD是否为鳖臑.若是, 写出其每个面的直角(只需写出结论);若不是,请说明理由. 解(1)因为PD⊥平面ABCD,所以PD⊥BC, 由于底面ABCD为长方形,有BC⊥CD,且PD∩CD=D,所以BC⊥平面PCD. 由DE⊂平面PCD,所以BC⊥DE. 又PD=CD,点E是PC的中点,所以DE⊥PC.由PC∩BC=C,得DE⊥平面PBC. 由BC⊥平面PCD,DE⊥平面PBC,可知四面体EBCD的四个面都是直角三角形,则四面体EBCD是一个鳖臑,其四个面的直角分别是∠BCD、∠BCE、∠DEC、∠DEB.


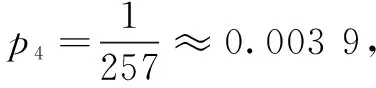
二、以学生为本







三、以素养为本







