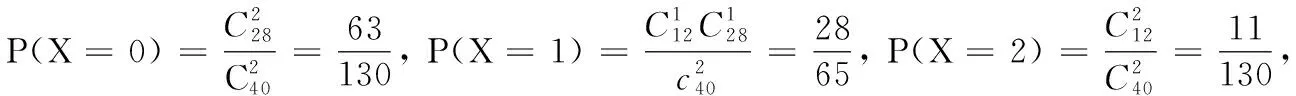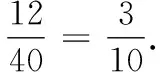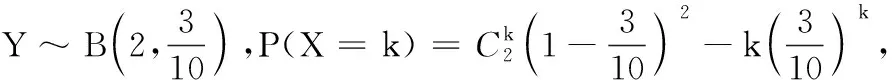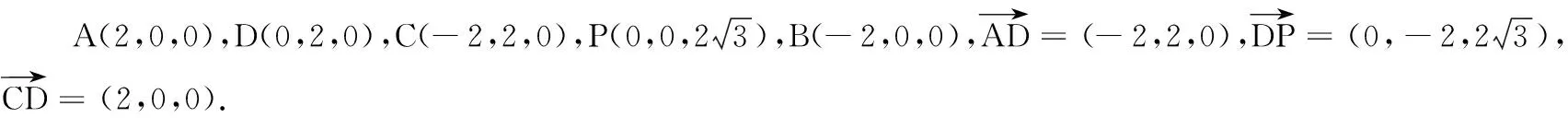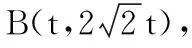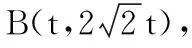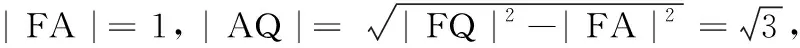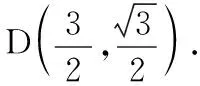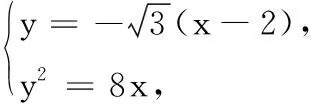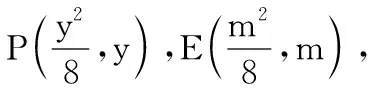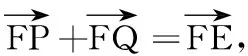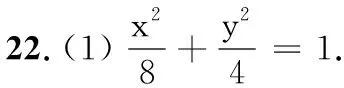高二数学测试

一、填空题(本大题共有12小题,每小题4分,共计48分)

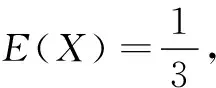
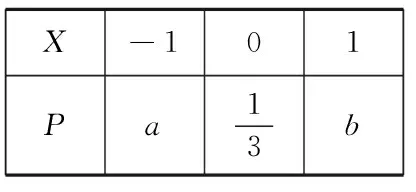
X-101 Pa13b

2.据统计,某城市的火车站春运期间日接送旅客人数X(单位:万)服从正态分布X～N(6,0.82),则日接送人数在6万到6.8万之间的概率为( ) (P(|X-μ|<σ)=0.682 6,P(|X-μ|<2σ)=0.954 4,P(|X-μ|<3σ)=0.997 4)

(A)0.682 6 (B)0.954 4

(C)0.997 4 (D)0.341 3

3.天气预报,在元旦假期甲地降雨概率是0.2,乙地降雨概率是0.3.假设在这段时间内两地是否降雨相互之间没有影响,则这两地中恰有一个地方降雨的概率为( )

(A)0.2 (B)0.3

(C)0.38 (D)0.56

4.已知盒中装有3个红球、2个白球、5个黑球,它们大小形状完全相同,现需一个红球,甲每次从中任取一个不放回,则在他第一次拿到白球的条件下,第二次拿到红球的概率为( )

5.8个人坐成一排,现要调换其中3个人中每一个人的位置,其余5个人的位置不变,则不同的调换方式有( )

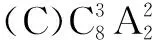
6.箱子里有5个黑球,4个白球,每次随机取出一个球,若取出黑球,则放回箱中,重新取球;若取出白球,则停止取球,那么在第4次取球之后停止的概率为( )

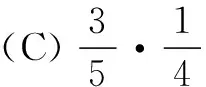
7.某车间为了规定工时定额,需要确定加工零件所花费的时间,为此进行了5次试验,根据收集到的数据(如下表)

加工时间y(min)62758189

(A)67.2 (B)68.2

(C)68 (D)67

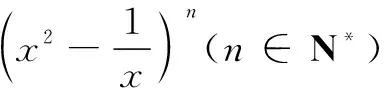
(A)12 (B)8 (C)6 (D)4

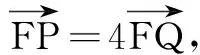
10.下列叙述中正确的是( )

(A)若a、b、c∈R,则“ax2+bx+c≥0”的充分条件是“b2-4ac≤0”;

(B)若a、b、c∈R,则“ab2>cb2”的充要条件是“a>c”;

(C)命题“对任意x∈R,有x2≥0”的否定是“存在x∈R,有x2≥0”;

(D)l是一条直线,α、β是两个不同的平面,若l⊥α,l⊥β,则α∥β.

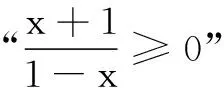
(A) [-2,-1]

(B) (-2,-1)

(C) (-∞,-2]∪[-1,+∞)

(D) (-∞,-2)∪(-1，+∞)

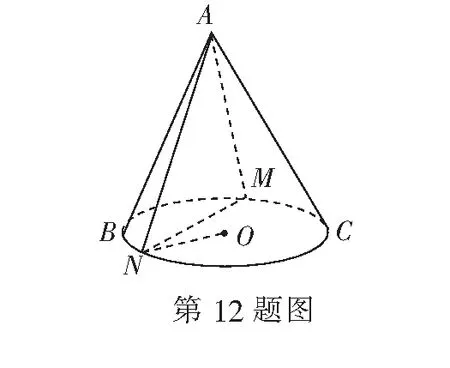
12.如图,M、N是圆锥底面圆O上不同两点,且M、N、O不共线,设AN与底面所成角为α,二面角A-MN-O的平面角为β,ON与平面AMN所成角为γ,则( )

(A)β>α>γ(B)β>γ>α

(C)α>β>γ(D)α>γ>β

二、填空题(本题有4小题,每小题5分,共20分.)

13.甲、乙两名射击运动员参加某大型运动会的预选赛,他们分别射击了5次,成绩如下表(单位:环):

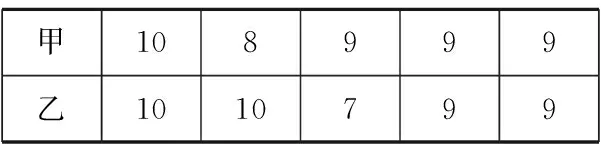
甲108999 乙1010799

如果甲、乙两人中只有1人入选,则入选的最佳人选应是______.

14.不透明的口袋中有形状和大小完全相同的四个球,球的编号分别为1,2,3,4.若从袋中随机抽取出两个球,则取出的两个球的编号之和小于5的概率为______.

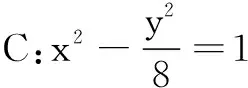
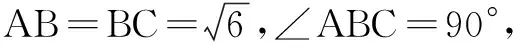
三、解答题(本题有6小题,共82分.解题时应写出必要的文字说明、证明过程或演算步骤.)

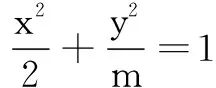
(1)若命题p为假命题,求实数m的取值范围;

(2)若命题p、q中有且只有一个是真命题,求实数m的取值范围.

18.(本小题满分14分)某食品厂为了检查一条自动包装流水线的生产情况,随机抽取该流水线上的40件产品作为样本称出它们的质量(单位:克),质量的分组区间为(490,495],(495,500],…,(510,515].由此得到样本的频率分布直方图如下图.

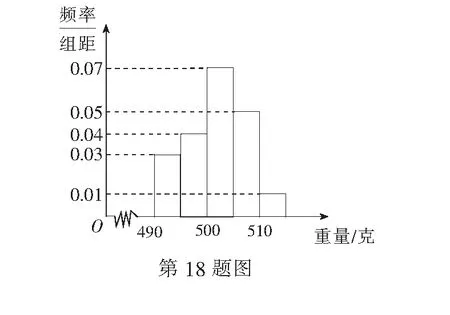
(1)根据频率分布直方图,求质量超过505克的产品数量;

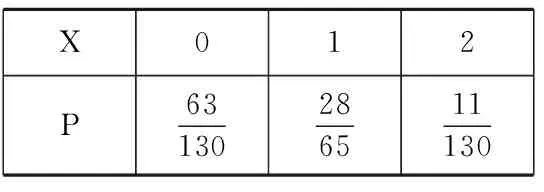
(2)在上述抽取的40件产品中任取2件,设X为质量超过505克的产品数量,求X的分布列;

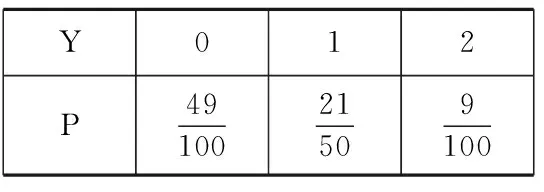
(3)从该流水线上任取2件产品,设Y为质量超过505克的产品数量,求Y的分布列.

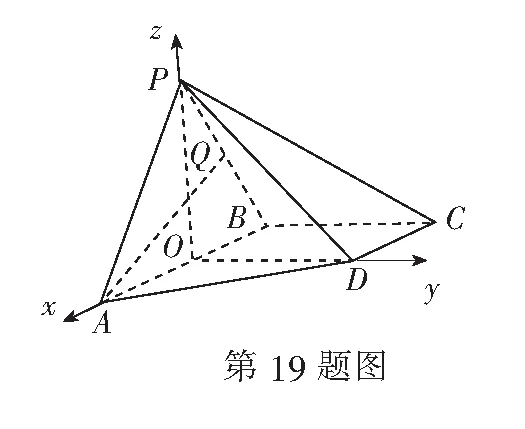
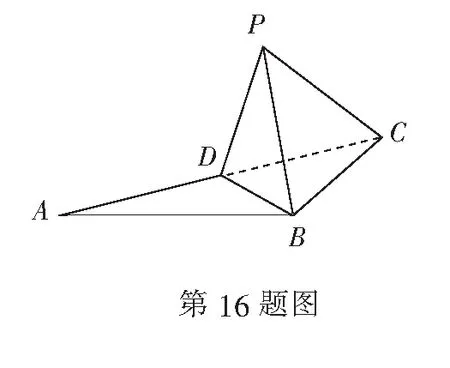
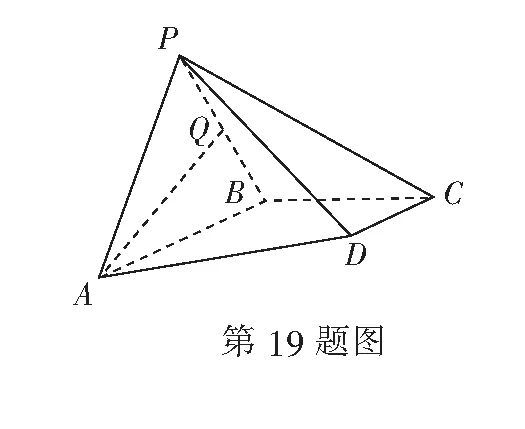
19.(本小题满分14分)如图,四棱锥P-ABCD中,AB∥CD,∠BCD=90°,AB=2BC=2CD=4，∆PAB为等边三角形,平面PAB⊥平面ABCD,Q为PB中点.

(1) 求证:AQ⊥平面PBC；

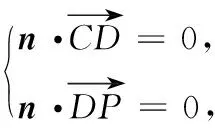
(2)求二面角B-PC-D的余弦值.

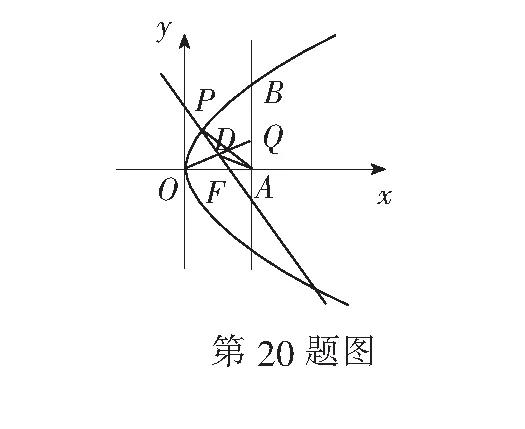
20.(本题满分14分)设常数t>2.在平面直角坐标系xOy中,已知点F(2，0)，直线l:x=t,曲线Γ:y2=8x(0≤x≤t,y≥0).l与x轴交于点A、与Γ交于点B.P、Q分别是曲线Γ与线段AB上的动点.

(1)用t表示点B到点F距离；

(2)设t=3,|FQ|=2，线段OQ的中点在直线FP，求∆AQP的面积；

(3)设t=8,是否存在以FP、FQ为邻边的矩形FPEQ，使得点E在Γ上？若存在，求点P的坐标；若不存在，说明理由.

21.(本小题满分14分)2019年春节期间,某超市准备举办一次有奖促销活动,若顾客一次消费达到400元则可参加一次抽奖活动,超市设计了两种抽奖方案：

方案1 一个不透明的盒子中装有30个质地均匀且大小相同的小球,其中10个红球,20个白球,搅拌均匀后,顾客从中随机抽取一个球,若抽到红球则顾客获得60元的返金券,若抽到白球则获得20元的返金券,且顾客有放回地抽取3次.

方案2 一个不透明的盒子中装有30个质地均匀且大小相同的小球,其中10个红球,20个白球,搅拌均匀后,顾客从中随机抽取一个球,若抽到红球则顾客获得80元的返金券,若抽到白球则未中奖,且顾客有放回地抽取3次。

(1)现有两位顾客均获得抽奖机会,且都按方案1抽奖,试求这两位顾客均获得180元返金券的概率;

(2)若某顾客获得抽奖机会.

① 试分别计算他选择两种抽奖方案最终获得返金券的数学期望;

② 为了吸引顾客消费,让顾客获得更多金额的返金券,该超市应选择哪一种抽奖方案进行促销活动?

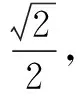
(1)求C的方程；

(2)若直线l是圆x2+y2=8上的点(2，2)处的切线，点M是直线l上任一点，过点M作椭圆C的切线MA、MB，切点分别为A、B，设切线的斜率都存在.求证：直线AB过定点，并求出该定点的坐标.

参考答案

一、选择题

1.B;2.D;3.C;4.B;5.C;6.B;

7.D;8.B;9.C;10.D;

11.A;12.A.

二、填空题

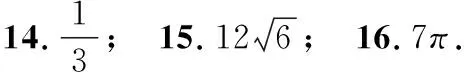
三、解答题

17.(1)p假:Δ<0，得m>1.

(2)p真:m≤1；q真:0

若p真q假,则m≤0；若p假q真,则1

综上，m≤0或1

18.(1)质量超过505克的产品的频率为5×0.05+5×0.01=0.3,所以相应产品数量为40×0.3=12(件).

(2)重量超过505的产品数量为12件,则重量未超过505克的产品数量为28件,X的取值为0,1,2,X服从超几何分布.

X012 P63130286511130

Y012 P4910021509100

19.(1)因为AB∥CD,∠BCD=90°, 所以AB⊥BC.又平面PAB⊥平面ABCD,且平面PAB∩平面ABCD=AB,所以BC⊥平面PAB；又AQ⊂平面PAB,所以BC⊥AQ.因为Q为PB中点,且∆PAB为等边三角形,所以PB⊥AQ,又PB∩BC=B,所以AQ⊥平面PBC.

(3)存在点P满足题设.

② 由①知E(X)>E(Z),所以该超市应选择第一种抽奖方案.

(2)依题设,得直线l的方程为y-2=-(x-2),即x+y-4=0.

设M(x0,y0)、A(x1,y1)、B(x2,y2),由切线MA的斜率存在，设其方程为y-y1=k(x-x1).

同理，切线MB的方程为x2x+2y2y=8,

又因为两切线都经过点M(x0,y0),所以

所以直线AB的方程为x0x+2y0y=8.

因为x0+y0=4,所以直线AB的方程可化为x0x+2(4-x0)y=8,即x0(x-2y)+8y-8=0.

所以，直线AB恒过定点(2，1).