浅谈平行结转分步法广义在产品数量确定
上海济光职业技术学院 李 娜
一、建立数学模型确定广义在产品数量
平行结转分步法,是将各生产步骤应计入相同完工产品成本的份额平行汇总,计算出完工产品成本的方法。平行结转分步法下,不计算各生产步骤的半成品成本,只计算最终完工产品成本,因此,也称作“不计算半成品成本的分步法”。运用平行结转分步法的难点是确定广义在产品的数量。
(一)建立数学模型确定广义在产品数量的必要性 广义在产品,是指从投产开始至尚未制成最终产品入库的产品。具体来看,各生产步骤的广义在产品包括两部分:一是正在各个生产步骤中生产加工的在产品,即狭义在产品;二是经过本生产步骤生产完工但尚未形成完工产品的所有半成品,包括处于后面各个生产步骤的在产品和经过本步骤及后面各步骤加工后转入半成品库的半成品(即经过本步骤生产但未形成完工产品的所有狭义在产品和入库的半成品)。根据广义在产品的概念,通常可以运用下述公式确定广义在产品数量(下面简称为概念公式):某步骤广义在产品数量=本步骤狭义在产品数量×折算比例+后面各步骤狭义在产品消耗本步骤半成品数量+本步骤库存半成品数量+后面各步骤库存半成品消耗本步骤半成品数量。但在具体核算中,广义在产品概念比较抽象,即使运用上述计算式,也经常会出现重复或遗漏某个项目的现象。为了能够用数学公式准确、快速地计算各步骤广义在产品数量。有必要建立确定广义在产品数量的数学模型。
(二)数学模型的构建 对于月末存在在产品的制造企业,其所归集的生产费用应由本期完工产品与月末在产品共同负担。完工产品成本与月末在产品成本之间存在如下勾稽关系:
月初在产品成本+本月发生的生产费用=月末在产品成本+本月完工产品成本
若把月初在产品成本和本月发生的生产费用视为本月总投入,则月末在产品成本和本月完工产品成本可视为本月总产出,满足“总投入=总产出”的关系。
从总投入方面来看,各步骤本月总投入产品数量=上月末广义在产品结转数量+本步骤本月投入产品数量=本步骤月初在产品数量(不考虑完工程度)+以后步骤月初在产品耗用本步骤半成品数量+本步骤本月投入产品数量=本月初广义在产品数量+本步骤本月投入产品数量。
从总产出方面来看,各步骤本月总产出数量=本步骤本月已完工的半成品(最后步骤为产成品)数量+本步骤月末正在加工的在产品数量(不考虑在产品的完工程度)=最终产成品耗用本步骤半成品的数量+本步骤已经完工并转到以后各生产步骤的完工半成品+本步骤正在加工的在产品数量=最终产成品耗用本步骤半成品的数量+本步骤月末广义在产品的数量。
根据“总投入=总产出”的思路,本步骤月初广义在产品数量+本步骤本月投入产品数量=最终产成品耗用本步骤半成品的数量+本步骤月末广义在产品的数量。假定连续生产企业每一步骤对前一步骤半成品的耗用比例为1:1,若不考虑月末在产品的完工程度,可以构建如下模型:
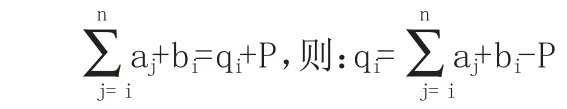
其中:

若考虑月末在产品完工程度,计算月末广义在产品数量时需将本步骤月末狭义在产品数量进行折算,则数学模型应变形为:
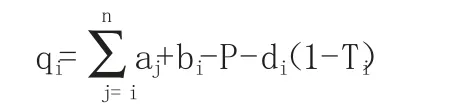
其中:

需强调的是,无论企业是否设置半成品库,即无论企业是否存在库存半成品,该模型均适用。但该模型不适用于装配生产企业,以及连续生产企业每一步骤对上一步骤半成品的耗用比例非1:1的情况。
二、数学模型的实例验证
分企业各步骤完工半成品不通过半成品库收发和通过半成品库收发两种情况,运用广义在产品数量确定的概念公式和数学模型同时计算广义在产品的数量,来验证模型的正确性。
(一)各步骤完工半成品不通过半成品库收发 第一、若不考虑在产品的完工程度。若各步骤完工半成品不通过半成品库收发且不考虑在产品的完工程度,根据广义在产品的概念,确定广义在产品数量的公式(下面简称概念公式)为:某步骤广义在产品数量=本步骤狭义在产品数量+后面各步骤狭义在产品消耗本步骤半成品数量+本步骤库存半成品数量+后面各步骤库存半成品消耗本步骤半成品数量。此时,广义在产品数量确定的数学模型为(下面简称数学模型)
[例1]长江公司20××年6月份生产甲产品328件,需经过第一、第二、第三车间连续加工完成。第一车间完工的半成品全部转移给第二车间加工(半成品成本不转移,仍保留在第一车间基本生产成本明细账内,下同);第二车间完工的半成品全部转移给第三生产车间生产出完工产品。该企业采用平行结转分步法计算产品成本。假定每一生产步骤的狭义在产品材料投料比例和完工程度均为50% ,假定每一步骤对前一步骤半成品的耗用比例为1:1。有关产量资料如表1:

表1 产量资料
(1)根据概念公式,各步骤广义在产品数量计算结果如下:
第一车间广义在产品数量=37+35+32=104件
第二车间广义在产品数量=35+32=67件
第三车间广义在产品数量=32件
第一车间广义在产品数量=(47+45+50)+290-328=104件
第二车间广义在产品数量=(45+50)+300-328=67件
第三车间广义在产品数量=50+310-328=32件
第二、若考虑在产品完工程度。若考虑在产品完工程度,需将本步骤狭义在产品数量进行折算,概念公式变形为:某步骤广义在产品数量=本步骤狭义在产品数量×折算比例+后面各步骤狭义在产品消耗本步骤半成品数量。此时,数学模型变形为-P-di(1-Ti)。
沿用[例1]中资料:
(1)根据概念公式,则各步骤广义在产品数量计算结果如下:
第一车间广义在产品数量=37×50% +35+32=85.5件
第二车间广义在产品数量=35×50% +32=49.5件
第三车间广义在产品数量=32×50% =16件
第一车间广义在产品数量= (47+45+50)+290-328-37×(1-50%)=85.5件
第二车间广义在产品数量=(45+50)+300-328-35×(1-50%)=49.5件
第三车间广义在产品数量=50+310-328-32×(1-50%)=16件
(二)各步骤完工半成品通过半成品库收发 第一、若不考虑在产品完工程度。若各步骤完工半成品通过半成品库收发核算且不考虑在产品完工程度,概念公式变形为:某步骤广义在产品数量=本步骤狭义在产品数量+后面各步骤狭义在产品消耗本步骤半成品数量+本步骤库存半成品数量+后面各步骤库存半成品消耗本步骤半成品数量。此时,广义在产品数量确定的数学模型为
[例2]长江公司20××年6月份生产甲产品1095件,需经过第一、第二、第三车间连续加工完成。第一车间完工的半成品需经过第二车间继续加工,第二车间完工的半成品需经第三车间继续加工才能生产出完工产品。该公司采用平行结转分步法计算产品成本,半成品通过半成品库进行核算。假定每一生产步骤的狭义在产品材料投料比例和完工程度均为50% ,假定每一步骤对前一步骤半成品的耗用比例为1:1。20××年6月份该公司有关产量资料如表2:
(1)根据概念公式,各步骤广义在产品数量计算结果如下:
第一车间广义在产品数量=80+66+89+(1020-1000)+(1080-1050)=285件

表2 产量资料
第二车间广义在产品数量=66+89+(1080-1050)=185件
第三车间广义在产品数量=89件
第一车间广义在产品数量=(120+146+134)+980-1050=285件
第二车间广义在产品数量=(146+134)+1000-1095=185件
第三车间广义在产品数量=134+1050-1095=89件
第二、若考虑在产品完工程度。若各步骤完工半成品通过半成品库收发核算且考虑在产品完工程度,概念公式变形为:某步骤广义在产品数量=本步骤狭义在产品数量×折算比例+后面各步骤狭义在产品消耗本步骤半成品数量+本步骤库存半成品数量+后面各步骤库存半成品消耗本步骤半成品数量。此时,广义在产品数量确定的数学模型为
沿用[例2]中资料:
(1)根据概念公式,各步骤广义在产品数量计算结果如下:
第一车间广义在产品数量=80×50% +66+89+(1020-1000)+(1080-1050)=245件
第二车间广义在产品数量=66×50%+89+(1080-1050)=152件
第三车间广义在产品数量=89×50% =44.5件
第一车间广义在产品数量=(120+146+134)+980-1050-80×(1-50%)=245件
第二车间广义在产品数量= (146+134)+1000-1095-66×(1-50%)=152件
第三车间广义在产品数量=134+1050-1095-89×(1-50%)=44.5件
综上所述,通过计算验证,应用数学模型与使用概念公式计算结果相同,而且使用数学模型计算思路清楚,可以准确、快捷地计算出广义在产品数量。
通过上述例题验证可以看出,无论考虑不考虑在产品的完工程度,也无论各生产车间设不设半成品库,通过模型aj+bi-P-di(1-Ti)”,均可准确计算月末广义在产品数量。但在使用模型时,要注意该模型只适用于连续生产车间,且每一步骤对前一步骤半成品的耗用比例为1:1的情况;同时也要注意若各生产步骤存在月初半成品,此模型需要进行适当调整。
[1]夏萍:《平行结转分步法下约当总产量确定》,《财会通讯》(综合·上)2011年第11期。

