关注数学基本活动，注重积累数学经验

梁奇

摘  要：“数学基本活动”的开展，是学生学习数学、积累数学经验的重要载体。而“数学经验”是无法教授的，只能依靠学生亲自参与活动，在实践中积累和感悟，它对提高学生数学核心素养具有重要的意义[1]。

关键词：数学基本活动;经验;积累

所谓的“数学基本活动经验”是指学生在经历数学活动以后形成的感知或基本活动经验等内容，可分为探究经验、操作经验、思考经验和应用经验。在课堂教学过程中，很多教师都比较关注怎样帮助学生积累“数学基本活动经验”。因此，笔者就如何亲历数学基本活动，在经验积累中得到提升展开分析。

一、亲历数学基本活动过程，提升操作经验

操作经验是根植于数学基本活动过程中的。在课堂教学中，通过数学活动机会的提供，学生能够感受活动过程，积累操作经验。但是，受各种因素的影响和条件的限制，不少教师将本该学生亲手实践的操作活动，简化为个别学生操作或示范，虽然学生通过教师或同学的示范也能理解活动所表达的含义，但是学生没有亲自动手操作，其操作经验的积累就受到了影响 [2]。“经验”具有明显的主观性特点，亲自操作为学生获取直接体验、感受和经验提供了基础，也是解决问题和探究问题的主要手段。因此，教师在课堂教学中要创造一定的条件，让所有学生亲身经历活动过程。

例如“圆柱与圆锥”的单元，其中包含不规则（石块、马铃薯等）物体的体积测算。在这部分内容的教学中，常规教学方法是引导学生观察多媒体演示或者通过板书画图进行思考，最后得出此类不规则物体体积计算的方法是算出上升部分圆柱体（水）的体积。在这种教学方法下，很多学生貌似掌握了不规则物体的计算方法，但在习题中，不少学生遇到放入水里的物体是圆锥体时，也将水上升的体积计算成圆锥的体积。由此可见，学生对转化的本质还没有真正理解透彻，这也是学生操作经验不足造成的弊端。因此，在学生了解测量的相关原理后，可设计如下教学活动。

活动要求：

1. 测量不规则石块的体积，四人小组合作;

2. 学生自主准备所需要的材料。

简述操作过程：大部分小组用圆柱体的透明玻璃杯当作量杯，先倒入适量的水，将直尺插入杯中测得水的高度，再投入石块，再次测量水的高度。之后测得杯底的直径，根据圆柱体积计算的方法，计算出石块的体积。

获得操作经验：

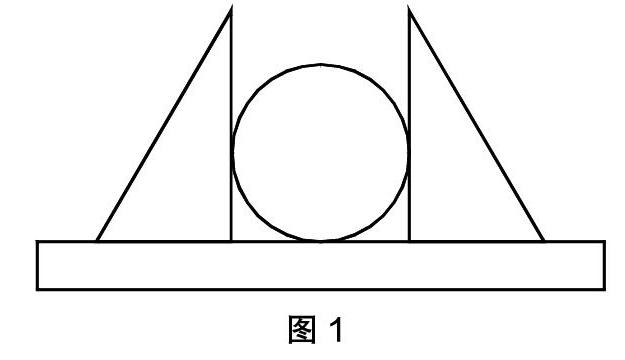
1. 亲历感受并掌握测量方法。在小组成员的通力合作下，学生基本掌握了不规则物体的体积测量过程和方法。在测量玻璃杯直径时，由于难以找到圆心，学生便开动脑筋，用两把三角尺和一把直尺（如图1）测得玻璃杯的直径，这种方法比课堂中所学习的测量直径的方法更贴合生活实际。

2. 材料的选取较灵活。测量容器的选择很重要，大部分学生选择了圆柱形的玻璃杯，也有小部分学生选择了圆柱形的饮料罐。在石块的选取时，大家都选择了小于测量容器口径的石块，便于操作。为了弥补玻璃杯没有刻度的不足，有学生将带有刻度的软尺贴到杯侧作为量杯的刻度。

3. 减少误差。有学生为了尽可能地减少石块吸水导致的误差，则将石块先泡水，再进行测量。纵然，每组测得石块的体积数据各异，精确度也有待考量，但是在石块体积的测量过程中，学生不但对不规则物体的体积测量有了更直观、深刻的理解，同时也获得了丰富的实践操作经验，为今后的实验操作夯实了基础。这些宝贵的经验，只有亲历实践、动手操作，才能真正获取。

二、提前“孕伏”，提升抽象概括经验

所有的数学活动，都是在“抽象”上进行的。学生一旦能从数学问题的现实情境过渡到“抽象”的模式，就已经掌握了这部分知识。新课标下的小学数学，为了让学生更好地体验生活与数学的关系，重点强调了与情境相结合。但在实际课堂中，教师通常忽略“去情境”的建模过程，使学生难以获取抽象概括的活动经验 [3]。例如，列方程解决实际问题时，教师较容易忽略抽象等量关系式。因为没有前期的铺垫，学生学习列方程解决实际问题时，难以叠加方程解法和概括等量关系式，在学习中出现了明显的障碍。笔者认为，想要解决这个问题，需提前孕伏等量关系式的相关知识。在低年级学习阶段，教师就可以渗透相关内容，如学习“比一个数多或少几的数是多少”时，可以让学生尝试感受关系式，例如“吴刚有6朵小红花，李明的小红花比吴刚多6朵，李明有几朵小红花？”这里出现的关系式为“李明的小红花数-吴刚的小红花数=6”，或“李明的小红花数=吴刚的小红花数+6”。当然，关系式并不需要用文字的方式表达，可以使用口述或图示的方法，让学生对等量关系式产生一定的认识。在中年级学习阶段则需要对“等量关系式”及“概括”的方法进行复习和整理。可以运用一些题目，让学生使用一些方法找到关系式：（1）以数量关系为依据寻找;（2）以计算公式为依据寻找;（3）以关键句为依据寻找……再根据这些方法，让学生理解“时间×速度=路程;数量×单价=总价;工作时间×工作效率=工作总量”等常用数量关系，同时学会概括一些不典型的数量关系，如“每份数×份数=总数”等。经过分层的孕伏，学生就积累了抽象概括的活动经验，分解了列方程解决实际问题的难点，学生将精力全部投入解方程之中，从而提高了课堂学习效率。

三、在交流中提升归纳推理的经验

归纳推理经验作为思考经验中的一类，对学生的学习活动和探究應用有着重要的影响。在小学数学教材中，需要归纳推理经验的内容有很多，如商的变化规律、积的变化规律、运算定律、比例的基本性质等。笔者根据“积的变化规律”这节课的教学片段，帮助学生积累归纳推理的经验。

展示：2×6=12;20×6=120;200×6=1200。

师：在这组算式中，同学们发现积有什么变化规律？

生1：每个积的末尾加了一个0。

师（将学生的回答进行板书）：你们觉得积的变化和谁相关？

（生：因数）在寻找积的变化规律时，除了找出不同算式积的变化关系，还要找出积的变化和因数变化之间的内在联系。

生2：算式中第一个因数有几个0，积也是几个0。

生3：积随着因数的变大而变大。

师（将学生的回答进行板书）：因数出现几个0，积就一定有几个0吗？（无学生回答，将这个问题留到课堂其他环节）积怎么随着因数的变大而变大的？

生4：当第一个因数多了十倍，积也大了十倍。

师：第二个因数呢？

生：第二个因数不变。

师：对，在寻找规律时，既要关注算式中变化的部分，也要关注算式中不发生变化的部分。（完成板书：第二个因数不发生变化，第一个因数多十倍，积也相应地增加十倍）

师：只有乘10吗？请举例。（生答略）

师：只有乘法吗？请举例。（生答略）

師：只限定第一个因数用来乘或者除吗？（生答略）

师（板书）：算式中一个因数不变，另一个因数乘或除以多少，积也相应地乘或除以多少。

师：这个规律我们是怎样概括出来的？（生答略）

师：探索积的变化规律，关键在于寻找各部分之间的联系，在已知的规律上进行思考和完善，然后使用简洁明了的语言表述。

在这个教学片段中，该教师从学生的认知水平和能力出发，充分肯定并鼓励学生每一次的合理归纳，通过逐层引导，在和谐的沟通与交流中，协助学生自主完善对积的变化规律的认知。在总结部分对所观察的顺序和对象进行概括，提升学生积累归纳推理的活动经验，也为后期的学习夯实基础。

数学活动经验对数学观念和数学思想的形成都起到了至关重要的作用，积累丰富的数学活动经验，对今后的数学学习能产生深远的影响，也是提高数学核心素养的根本。因此，作为一线的小学数学教师，在教学过程中，需要从各个环节落实并实施，协助学生积累数学基本活动经验，以提高数学综合素养。

参考文献：

[1]  张丹. 数学实践活动与儿童核心素养发展关系思考[J]. 长春师范大学学报，2017（12）.

[2]  朱国晖，郑芳. 小学数学教学中实践与综合应用能力的培养[J]. 中国科教创新导刊，2009（27）.

[3]  黄红梅. 如何引导小学生积累数学学习经验[J]. 西部素质教育，2018（7）.