思维导图:可视化教学的重要利器
胡全会
摘 要:作为学生“可视化学习”的一种有效工具,思维导图能有效地组织学生学习。在小学数学教学中,思维导图能完善数学知识结构,能协同左右大脑活动,能引导学生数学思维。借助思维导图,能让数学知识直观展现、能让思维唾手可得、能让学习有迹可循。运用思维导图进行数学学习,学生的直觉思维力、逻辑思维力等都能得到有效提升!
关键词:小学数学;思维导图;可视化教学
当下,数学教学已经从知识取向转向核心素养取向。发展学生数学核心素养,需要激发学生数学思维,优化学生的学习品质。可视化教学,不仅能将隐性的数学知识显现出来,而且能敞亮学生的数学思维。作为学生“可视化学习”的一种有效工具,“思维导图”能有效地组织学生学习。思维导图,又称之为“心智地图”“脑力激荡图”“灵感触发图”。所谓“思维导图”,是指“用文字、图形等表达知识形成过程、知识结构的记忆、思维与想象工具”。思维导图,能将抽象的数学符号转化为容易记忆、理解、操作的图形、图像、图表等。
一、思维导图:意义及其价值
思维导图发端于20世纪80年代的英国,其创始者为托尼·博赞(Tony Buzan)先生。数学教学中,常用的思维导图主要有“线段图”“指示图”“几何图”“草图”等,因而思维导图是一个简单、有效、美丽的思维工具。借助于思维导图,能有效地发掘学生数学学习潜质,让学生展开全面的、整体的、和谐的学习活动。
1. 思维导图能完善数学知识结构
数学知识是整体性、系统性的结构。但在教材中,为了适应学生的学习心理,常常以“点”的形态展现。思维导图,能将零散的、分散的数学知识点进行集结,从而能建构、完善数学知识结构。美国著名教育家布鲁纳认为,“任何知识都有结构性,知识结构可以促进学生智力的发展”。运用思维导图,可以让学生深刻理解数学知识的本质,清晰地把握数学知识结构,从而有助于完善学生的认知结构。
2. 思维导图能协同左右大脑活动
基于“全脑教育”理念,思维导图是按照人的大脑活动规律、思维规律而研发的一种思维工具。研究表明,人的大脑有着不同的分工。一般而言,人的左脑负责逻辑思维,右脑负责形象思维。借助思维导图,能极大地激活学生大脑中的图像、记忆、想象、颜色、空间、语言等各功能。思维导图,能让学生的大脑运作更稳健、更灵活。从这个意义上说,思维导图能让学生健康用脑、和谐用脑、友善用脑。
3. 思维导图能引导学生数学思维
学生的思维犹如宇宙中的黑洞,我们不能直视它。但借助思维导图,可以将学生深不可测的、神秘的黑洞敞开、洞察。德国著名物理学家、思想家爱因斯坦所说,“我不用语音思考问题,而是运用一幅幅能动的、跳动的图像来思考”。在数学学习中,学生可以将思维“写”下来、“画”下来,从而让思维有迹可循、触手可及。在思维导图引导下,学生的思维不再是静态的、深不可测的黑匣子,而是能动态地展现。正是在这个意义上,思维导图的创设人托尼·博赞先生说“思维导图是一把‘瑞士军刀,是可视化教学的‘利器”。
二、思维导图:策略及其路径
美国图论专家哈里说,“千言万语不及一张图”。在数学教学中,运用思维导图,不仅能让数学知识有序化、结构化,更能让学生的数学思维可视化、清晰化。思维导图,让抽象的数学知识更容易被直观、被认知、被想象。借助于思维导图,学生从被动学习转向主动学习。学生能对数学知识进行意义建构、意义反思、意义整合。
1. 思维导图:让知识直观展现
长期以来,我们总是批判唯知识论,导致许多教师、学生在数学学习中轻视知识。其实,知识是学生数学学习的根基,“无知必然无能”。但数学知识是抽象的、概括化的及形式化的。如何让抽象的数学知识形象化、直观化?笔者认为,教师可以借助思维导图,展示、展现、袒露数学知识的本质。借助思维导图,数学知识能变得直观、可感。
比如“乘法分配律”是小学数学“运算律”部分最为抽象的数学知识,学生在运用中经常将“乘法分配律”与“乘法结合律”混淆,张冠李戴、模糊不清。在数学教学中,笔者借助“长方形图”和“点子图”,将“乘法分配律”的内在算理直观地展现出来。在数形结合的过程中,学生逐步理解了乘法分配律的数学本质。在数学教学中,教师还可以出示一些“开放性”“半开放性”“逻辑性”“半逻辑性”的图。比如30×(7+6)=30×□+30×□,30×(7+6)=□×7○□×6,比如30×(5+6)=□○□○□○□,等等。这样的完形填空、不完形填空,犹如一个召唤结构,能召唤学生主动地对之进行补白、填空,从而不断地深化学生对乘法分配律的理解。一方面,将数学知识直观展现;另一方面,能活化学生的数学思维,让学生进行能动地认知、想象、推理,从而完成对数学知识的深度建构。
思维导图,能让数学知识直观展现。借助思维导图,学生能完成对数学知识的由此及彼、由浅入深、由表及里的建构。借助思维导图,学生对数学知识的认知、理解、建构将更加清晰、更加牢靠。思维导图,让知识直观展现。
2. 思维导图:让思维触手可及
由于年龄特征、心理特征等因素的制约,学生对数学知识的理解、建构有时往往是蜻蜓点水、浮光掠影的。作为教师,可以充分运用思维导图,让学生的思维触手可及。思维导图又被称为心智图,是基于对人脑的模拟,契合大脑的认知方式。在思维导图中,我们可以清晰地看到学生的思维状态、思维方向、思维路径、思维策略等。借助于思维导图,在触摸到学生的数学思维之后,教师可以有效地激发学生的数学思维。
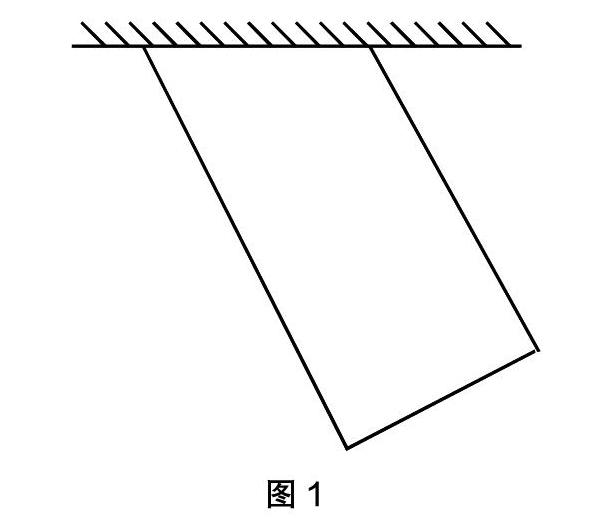
比如教学“梯形的面积”,学生遇到了靠墙围篱笆的情境(如图1),同时,这道习题打破了传统的已知梯形的上底、下底、高,要求梯形的面积的问题;而是已知篱笆的总长度以及篱笆的高,要求篱笆围成的图形的面积。在解决这个问题时,许多学生都理不清头绪,有学生看不懂题意,不知道墙在哪里;有学生虽然能看清题意,但却找不到解决问题的路径,等等。为此,笔者运用思维导图,在问题和条件之间架设桥梁,从而引导学生的数学思维。借助于思维导图,学生能主动进行思考、探究,从而能让学生认识到:要求梯形的面积,只要知道梯形的上下底的和、高就行了。这样的问题解决策略、步骤,反而要比已知梯形的上底、下底和高来得更方便、更快捷些。这样的思维导图,能打破学生的思维定式,让学生产生顿悟、灵感。同时,学生的数学思维也在导图中得到了体现。
思维导图能调动学生的已有知识经验,让学生依托已有知识经验进行思维。通过思维导图,学生的数学思维更灵动、更有生机和活力。他们能对数学问题进行主动思考、探究。思维导图改变了学生的认知方式,能让学生主动画图、操作,主动寻求未知与已知之间的关系,主动寻找解决问题的策略、路径、方法。
3. 思维导图,让学习有迹可寻
思维导图有助于学生进行主动学习。过去,学生往往在教师的牵引下进行数学学习,这样的学习是被动的、机械的、亦步亦趋的。思维导图,赋予了学生数学学习的充分时空,让学生能主动进行数学学习,让学生的数学学习有迹可循。在教学中,学生以思维导图为媒介、载体、抓手,教师只需要对学生的数学学习进行点拨、启发,就能开拓学生的创造性思维。
比如教学“角的认识”,笔者用表格建构了一个思维导图:小于90°的角、等于90°的角、大于90°而小于180°的角、等于180°的角、等于360°的角,等等。在思考、探究的过程中,学生借助于两根小棒,让其中的一根小棒围绕另一根小棒旋转,从而依次、分别得到了锐角、直角、钝角、平角、优角、周角等。在建构角的过程中,有学生认识到,有些角的度数是确定的,有些角的度数是不确定的。如此,不僅让学生掌握了应掌握的知识,而且还拓展了学生的认知,让学生认识了劣角、优角等。由于学生是动态地建构、认知,因而将知识点融为一个整体。学生不仅理解了角的定义,更理解了角的分类、角与角之间的关联,等等。在思维导图的引导下,学生的数学学习变得更主动、更积极了,学生的数学学习变得有迹可循了。
思维导图是学生数学学习的支架,犹如一根拐杖,不仅能将数学知识衔接起来,更能疏通学生的思路。学生在数学学习中,能够循着思维导图的方向、路径,调适自己的数学学习。教学中,学生还可以自主画图,将数学知识的关系勾连起来、集约起来,将自己的思维展示出来。如此,数学学习就将从零散走向集约、从粗放走向精致、从朦胧走向清晰。在运用思维导图进行学习的过程中,学生的直觉思维力、逻辑思维力等都能得到有效提升!

