基于自适应多元变分模态分解的电力系统低频振荡模态辨识

刘乃毓，蔡国伟，杨德友，王博闻

(1.东北电力大学电气工程学院，吉林 吉林 132012；2.中国电力工程顾问集团东北电力设计院有限公司，吉林 长春 130022)

电力电子设备的广泛应用以及大规模新能源并网导致电网在受到冲击后低频振荡的非平稳、非线性问题日益严重[1].为保证电力系统平稳运行，需对低频振荡模式进行准确有效地辨识.

特征分析法基于电力系统数学模型建立全系统的线性状态方程，从而对系统的静态稳定进行分析，由于实际系统维度高，导致特征分析法易产生“维数灾”问题[2].向量测量装置(Phasor Measurement Unit,PMU)的发展为低频振荡的分析和辨识提供了新的平台.通过各类辨识手段可以从PMU量测信号中辨识振荡模式，避免了“维数灾”的问题.Prony算法通过对指数项等距采样数据拟合辨识信号振荡信息，该方法广泛应用于辨识低频振荡模式[3]，但其抗噪能力较差.文献[3]和文献[4]分别将形态滤波和滑窗处理与Prony算法结合，在一定程度上降低了噪声的影响.希尔伯特-黄算法(HHT)同样广泛用于处理非线性、非稳定问题，通过经验模态分解法(EMD)将输入信号分解为多个固有模态(IMF)，并利用希尔伯特变换得到各IMF振荡频率和幅度，但该方法受限于其核心算法EMD.EMD在处理信号时易受噪声的影响，从而导致模态混合和虚假模态等问题[5-7].为解决该问题提出了其衍生算法EEMD法，该方法基于白噪声的均匀分布特性，对信号多次分解后进行平均处理以消去噪声的影响[8].文献[9]与文献[10]通过改进EEMD滤波器以及矩阵束算法与EEMD算法结合的方法，有效地降低了噪声对振荡参数辨识的影响，但其复杂的计算过程导致了运行时间过长的问题[11].变分模态分解法(VMD)具有抗噪能力强、辨识精度高等特点[12-13]，目前广泛应用于信号分解与参数识别，但VMD的精准程度受其模态设定值K的限制，K值需要人为设定，并且该方法不能对多元数据进行分解[14-15].文献[14]通过窗口傅里叶变换法(WFT)确定K值，但存在不能对多元信号同时分解的问题.为了解决多元数据分解的问题，基于EMD算法提出了MEMD算法，该算法虽然可以进行多元数据分解，但其基本原理与EMD相同，同样继承了EMD算法易受噪声影响的特点[16-17].

为解决以上问题，本文提出的一种自适应多元变分模态分解算法对多元信号进行辨识分解.自适应MVMD法继承了VMD方法的抗噪能力，有效避免了模态混叠，并可以通过模态复原近似度自适应确定模态设定值K，利用该算法对多元多模态耦合信号进行分解后，通过Hilbert变换提取各分离模态的振荡参数，并且通过构建多元解析信号集合解决了VMD算法及其衍生算法不能同时对多元信号进行辨识的问题.通过对测试信号及仿真信号的分析可以看出，自适应MVMD算法解决了K值确定困难的问题，可以准确有效地分离多元多模态耦合信号，同时可以对不同信号中相同频率模态进行辨识，并且该算法具有良好的抗噪能力.

1 自适应多元变分模态分解算法

MVMD与VMD一样作为一种非递归的分解方法，通过构造变分优化问题以分离包含在多元输入信号中的固有振荡模式，多元信号中各模式对应的带宽和中心频率在约束变分模型的限制下，经过迭代更新达到最优值.

1.1 多元约束变分模型的构建

MVMD算法将多元信号中K个固有模态函数转化为一组AM-FM信号u(t)，解析信号集合为

(1)

公式中：ai(t)和φi(t)分别为第i个信号分量相对应的幅值函数和相位函数.利用Hilbert变换获得和矢量信号u(t)对应的解析信号u+(t)为

(2)

由公式(2)可见，u+(t)由原矢量信号u(t)和经希尔伯特变换的Hu+(t)构成.取谐波混合信号的L2范数的平方获得u(t)的带宽.针对矢量信号集合u(t)带宽的约束变分优化模型为

(3)

公式中：k、c分别为分离模态数和输入信号数；∂为微分算子；ωk为分解后各模态中心频率；xc(t)为多元输入信号的集合；uk，c(t)为分离信号的集合.公式(3)中上式是一个不等式约束条件，其目的是使从c个信号中分离的uk，c(t)的带宽和最小，同时为了确保分离后各模态的精确性，通过公式(3)中的等式约束进行信号重构，保证重构信号与原信号相等.

1.2 多元约束变分模型求解

为使约束变分限制转变为无约束变分问题，利用拉格朗日乘数法对公式(3)进行构造，并引入α和λ(t)确保其满足约束条件，根据公式(3)构造的拉格朗日函数为

(4)

公式中：α为惩罚因子，其作用是提高算法的抗噪性；λ(t)为拉格朗日乘子，使变量不受约束.通过交替方向乘子法(ADMM)可将公式(4)中完整的优化问题转化为一系列子优化问题，并通过迭代对各子问题进行更新求解以得到多元信号的最优模态及最优中心频率.利用ADMM法简化后的二次子优化问题可以在频域内解决.

(5)

(6)

(7)

1.3 基于复原近似度的自适应MVMD算法

MVMD算法如VMD算法一样，在进行模态分离时需对模态数K进行人为设置，若K值设定过小会使模态分离不充分，导致模态混叠和缺失，若K值设定过大则会导致对信号的过度分离，从而产生虚假模态，影响辨识结果的准确性.因此，为了准确地确定模态数K，本文引入复原近似度η对K值进行估计.

图1 自适应MVMD算法流程图

(8)

3 基于MVMD-Hilbert的模态参数辨识

自适应MVMD算法将多模态耦合的低频振荡信号分离成多个固有模态，通过对各模态进行希尔伯特变换可以获得其振荡参数，步骤如表1所示.

自适应MVMD通过对多信号带宽和以及中心频率的约束变分问题迭代求解，将多元信号分离为K个固有振荡模式.通过MVMD算法将多模态耦合的多元低频振荡信号进行分解，可以实现各低频振荡模态的辨识和分离，并可以辨识出不同采样信号中相同频率的振荡模式.MVMD算法通过对变分约束模型设置惩罚因子有效地规避了噪声的影响，同时通过信号重构约束保证了模态分解的精确性，因此，可以保证基于希尔伯特变换对分离后的多元信号模态进行参数辨识的精确性.

表1 希尔伯特变换步骤

3 仿真分析

3.1 测试信号分析

为验证算法的有效性，首先采用公式(9)所示测试信号进行验证分析.该信号由二元信号构成，两信号均含2个主导模式，信号1两模式频率为0.4 Hz和1.8 Hz，信号2两模式频率为0.2 Hz和1.8 Hz，其中两信号均设置频率为1.8 Hz的主导模式以验证MVMD算法对多元信号相同模式辨识的有效性，叠加30 dB高斯白噪声的信号，如图2所示.

(9)

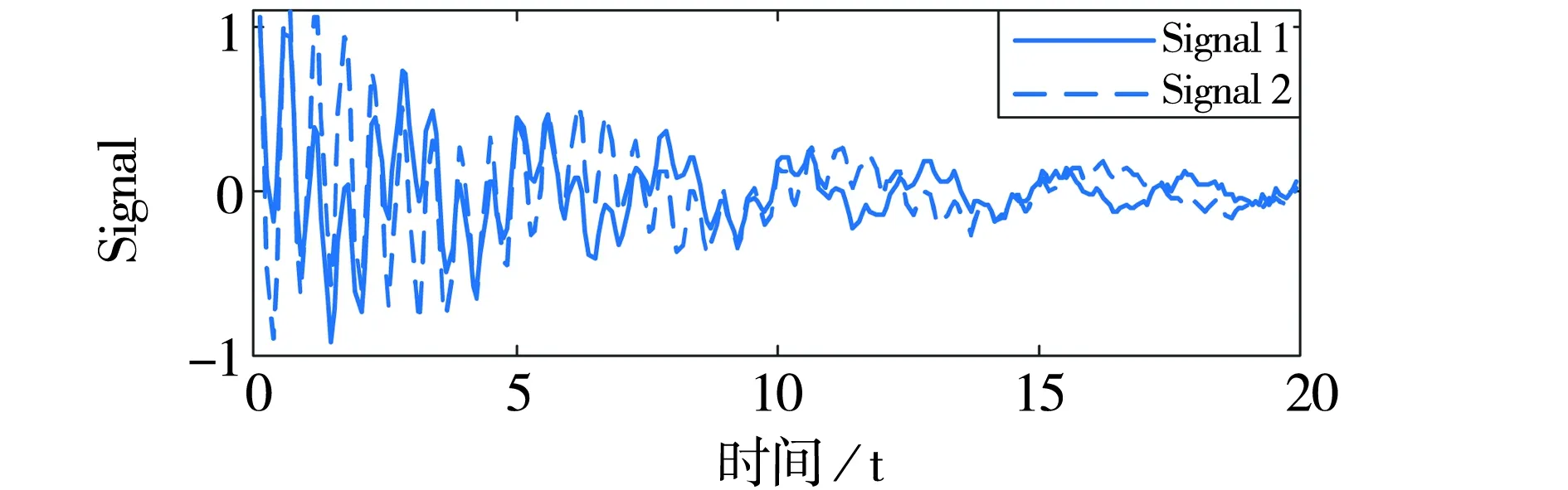
图2 含噪声测试信号

基于复原近似度η对K值进行选取，当K=2时获得最复原大近似度为53.547 7 dB和57.085 4 dB.在K=2时基于本文的自适应MVMD算法分解的结果，如图3所示，两信号均辨识出2个主要模态分量，且对频率为1.8 Hz的相同模式进行了辨识分类.为进一步验证模态辨识的准确性，利用WFT对各模态进行频谱分析，辨识结果，如图4所示.辨识后的两信号分离模态频率分别为0.401 Hz、1.805 Hz和0.201 Hz、1.810 Hz，与测试信号频率0.4 Hz、1.8 Hz和0.2 Hz、1.8 Hz近似相同，可见自适应MVMD在噪声的影响下可对多元信号进行有效分离，具有较好的辨识精确度，并可对多元信号中相同频率模态进行提取.

图3 测试信号MVMD分解图图4 MVMD分解模态WFT频谱图

为验证MVMD算法的优越性，利用经验模态分解法对附加噪声的测试信号进行辨识，辨识结果，如图5所示.由于两信号情况相似，仅以信号1为例进行对比分析.信号1经EMD分解后得到4个IMF分量以及一个剩余分量，利用EMD分解后模态数多于测试信号的模态数，产生了2个虚假模态.利用WFT对经EMD分解的信号1各模态进行频谱分析辨识结果，如图6所示.

表2 测试信号复原拟合度对比

通过图6可见，IMF1与噪声混叠，IMF1和IMF2均含有多个模态，出现了严重的模态混叠，且出现频率为0.352 Hz、0.201 Hz的虚假模态IMF3和IMF4，对振荡参数辨识影响极大.利用信号复原近似度和Hilbert变换对分离模态的振荡参数进行辨识，进一步对本文方法的有效性进行验证，结果如表2和表3所示.可以看出由自适应MVMD法分解获得的模态频率与阻尼比接近于理论值，且复原近似度较大，辨识精确度较高，而HHT算法受限于EMD抗噪能力差的问题，辨识的各模态参数偏差相对较大，且复原近似度远小于本文方法.

表3 测试信号主要模态结果

图7 联络线6-31、2-30有功信号

由以上分析可以看出本文方法可对多元信号准确分离，并能对多元信号中相同频率模式进行识别，同时具有较强的抗噪性.

3.2 仿真信号分析

以新英格兰10机39节点模型作为算例，基于Digsilent/PowerFactory平台在节点3处设置0.1 s的三相短路故障，并对6-31及2-30联络线有功信号进行分析，仿真信号，如图7所示.

为验证本文方法的抗噪能力，对以上信号叠加30dB高斯白噪声，利用本文方法对其进行分解，当K=2时复合近似度最大，模态分解结果及WFT频谱图，如图8和图9所示.通过两图可见，两信道信号分别包含两种主要模态分量.为验证模态分解的准确性，利用复原近似度及Hilbert变换提取振荡参数进行验证，并与HHT法进行比较，结果如表4和表5所示.由表4可见，自适应MVMD法分离模态频率分别为1.052、0.632和1.105、0.637Hz，获得频率与QR法计算的理论模态相吻合，其频率及对应阻尼比与计算结果相比误差较小，且并未产生虚假模态，同时也对双信道中均包含的区间振荡模式0.639 Hz分量进行辨识提取.相反HHT法由于抗噪性较差，出现了模态混叠，导致辨识结果误差较大，并且还有模态缺失的问题.

图8 仿真信号MVMD分解图图9 仿真信号MVMD分解图

表5 测试信号复原拟合度对比

信号复原近似度，如表5所示，采用自适应MVMD方法的模态近似度为29.375 7 dB和31.249 8 dB，远大于HHT法的近似度.由以上分析可见，本文方法具有良好的抗噪性，且规避了HHT方法中由于噪声导致的模态混叠以及虚假模态等问题，可对多元信号精确分解.

4 结 论

本文将自适应MVMD方法应用于电力系统多元低频振荡信号辨识中，并基于MVMD-Hilbert方法对振荡参数进行提取，通过对测试信号及仿真信号的分析获得结论如下：

(1)通过将模态复原近似度与MVMD算法结合，改善了MVMD自适应性的问题；

(2)自适应MVMD算法通过设置惩罚参数α提升了算法的抗噪性，规避了EMD算法中模态混叠及虚假模态等问题；

(3)自适应MVMD算法通过构建多元模态集合，使该方法可对多元振荡信号进行分解，同时可对不同信号中相同频率模态分类提取，解决了传统VMD及其衍生算法不能进行多元信号辨识的问题.

本文方法可精确辨识多元信号模态，并基于Hilbert变换提取振荡参数，是一种有效的辨识方法.如何提高计算速度以实现在线应用是下一步研究工作.