多端柔性直流输电系统运行状态评判

陈继开，贾肖华，辛业春，李林，王振浩

(东北电力大学电气工程学院，吉林 吉林 132012)

随着智能电网建设步伐的不断加快，电网结构日益复杂，为了保证系统运行安全，需要对系统各类运行进行准确的辨识与评价.因此，建立一套系统运行状态的评价指标体系并提出一种运行状态评判方法对系统状态分级评判具有很重要的意义.文献[1]运用鱼骨图法建立了评价指标体系，可以全面的对微电网进行分析评判.文献[2]与文献[3]分别利用不同的方法建立了一套评价指标体系，能够对电网的坚强度进行评判.文献[4]基于拉格朗日函数确定指标权重，能够评判配电网的运行方式.文献[5]采用两级模糊综合评判法对配电系统评价，能够对系统的运行趋势提供预警.文献[6]基于模糊最小二乘支持向量机法微电网群运行状态进行有效分类.文献[7]采用直觉模糊层次分析法定量评估电网系统的风险，能大大提高电网的安全性.

通过上述分析可知，目前所用的状态评判方法大多数运用在电网及电网设备的可靠性、坚强度评估上，并且所应用的领域主要集中在配电系统，智能电网，变压器设备评价等方面，而针对多端柔性直流输电系统整体运行状态分级评判研究还比较少，如果提出一种综合评判方法，能够准确的判断MMC-MTDC输电系统的不同运行状态健康等级，将对MMC-MTDC输电系统的运行优化控制提供有力的技术支撑.综上所述，本文提出一种主观与客观相结合的IAHP——反非广延熵权的评判方法，并应用于对系统运行状态的分级评判，最终从实验证明了该方法的正确性.

1 MMC-MTDC输电系统

1.1 MMC-MTDC输电系统的结构

MMC-MTDC输电系统是由三个以上换流器，通过串、并、混联等方式进行连接的输电系统[8].本文研究的MMC-MTDC输电系统是并联方式的环网结构，主要由：风场侧换流器、集群风场、网侧换流器、交流系统和直流系统等五部分组成，如图1所示.

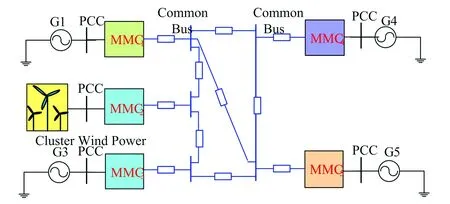
图1 集群风电场MMC-MTDC输电系统模型

1.2 影响MMC-MTDC输电系统运行的因素

1.2.1 不同运行工况对MMC-MTDC输电系统的影响

利用MMC-MTDC系统进行大规模集群风电电能外送是未来实现新能源高效利用的有效手段.当风场风速骤变时，一方面MMC-MTDC输电系统内传输功率随之变化，导致直流母线电压发生偏差，进而使与MMC换流器联接的交流系统发生频率偏移；另一方面风功率波动可能导致网内潮流分布更复杂，将会影响原来的运行方式，系统稳定运行点可能出现变化，继而影响系统的运行效率、可靠性和安全性.

当MMC-MTDC输电系统潮流反转时，因为MMC具有交流电压控制能力，所以对交流侧的电压影响很小，会保证系统交流侧的稳定性.为了实现潮流反转，系统内各换流站将切换到新的控制模式，在保证系统的直流侧电压极性不变的前提下，实现直流电网内电流方向的改变.在该过渡过程中，换流器通过的功率和直流母线电压将发生波动，相应各换流器承担的功率也随之改变，继而影响到系统的稳定性.

因为在潮流反转时直流侧电压方向不变而直流电流方向改变这个特点，当MMC-MTDC输电系统风场侧换流器退出运行时，在站间协调控制方法下，整个系统不会像双端直流输电系统那样必须停止运行，其它换流器之间仍可进行功率传输.但由于各个换流器协调过程中直流网内功率瞬间波动，同时功率重新分配，直流母线电压将会变化，所以系统的平衡工作点也会发生改变.

1.2.2 下垂控制策略对MMC-MTDC输电系统的影响

为了完成对MMC-MTDC输电系统的统一协调控制，根据不同的控制目标和运行要求，各换流站常采用不同的控制方法，以实现最佳的控制效果.以逆变站为例，以Udc的稳定为约束，为了合理的完成各站间功率分配，常采用功率-电压(P-U)下垂控制策略，由于下垂系数自适应算法的引入，改进下垂方法与下垂传统方法对系统的控制效果存在较大差异.

P-U下垂控制是根据下垂特性随换流器功率变化调节换流器直流母线电压继而实现站间功率分配的一种协调控制方法.当受端换流器直流母线电压增加时，接受功率在下垂控制的作用下将降低，这可以缓解由于功率激增(跌落)对换流器及交流系统的影响，并有效实现各换流器间功率的合理分配.同样，换流器直流母线电压下降意味着接收功率上升.但研究证明[9]，传统下垂控制不能实现潮流的精确控制、直流电压工作点不稳定，其本质为有差调节，造成的偏差越限会影响系统的稳定性.

改进下垂控制的下垂系数可以根据系统运行工况自适应调整，并将平移下垂曲线和改变下垂曲线的下垂系数相结合[10].它可以实现系统扰动引起的不平衡有功功率的合理分配.根据换流器的备用容量，改进下垂控制不仅可以释放MMC-MTDC输电系统的潜在无功功率控制能力，而且可以将不平衡有功功率合理地分配给每个换流器控制效果优于传统下垂控制方法.

2 评价指标体系建立

2.1 评价指标的选取原则

影响MMC-MTDC输电系统运行的因素有很多，科学全面的选取指标是MMC-MTDC输电系统运行状态分级评判的首要条件.因此设计指标体系时应依据科学性、针对性、系统性、可操作性和先进性原则来进行指标的筛选[11].

根据1.2节分析可知，功率、电压、频率、动态响应、可靠性、灵敏度这六个方面能够较为全面的反映系统运行的主要特征.因此，本文将以上六个方面作为指标选取的方向，按照上述评价指标选取的基本原则，筛选能够反映系统性质的指标，从而构建指标体系，如图2所示.

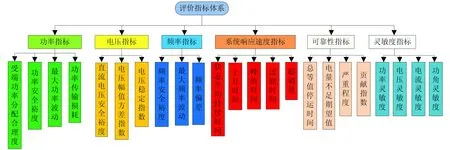
图2 评价指标体系

2.2 指标集的构建

2.2.1 功率指标

(1)受端功率分配合理度

合理的分配功率，能够使系统稳定安全的运行.

(1)

公式中：n个换流站分配功率，第l个换流站的容量为Sl，实际分得的功率为Pl.

(2)功率安全裕度

为了确保系统稳定安全的运行，换流站必须运行在功率的有效范围即功率安全裕度内[12].

(2)

公式中：P为换流站有功功率；PH=Pref(参考值)+ΔPmax为功率的上限；PL=Pref(参考值)-ΔPmax为功率的下限.

(3)最大功率波动

(3)

公式中：Pmax为功率最大值；Pmin为功率最小值；PN为功率的额定值.

(4)功率传输损耗

(4)

公式中：m个与系统相连的风场；Pwj为第j个风功率；Pslack为松弛功率.

2.2.2 电压指标

(1)换流站直流电压安全裕度

(5)

公式中：Udc为换流站的直流电压；UdcH为电压的上限；UdcL为电压的下限.

(2)电压幅值方差指数

能够检查系统是否在工作极限电压之间运行.

(6)

公式中：Vc为临界点处的电压大小；∂Vc/∂Pwj为Vc对Pwj的敏感性.

(3)电压稳定指数

(7)

公式中：Z为阻抗；X为电抗；Qj为受端无功功率；Vi为送端电压.

2.2.3 频率指标

(1)频率安全裕度

(8)

公式中：f为换流站的频率；fH为频率的上限；fcL为频率的下限.

(2)最大频率波动

(9)

公式中：fmax为频率最大值；fmin为频率最小值；fN为频率的额定值.

(3)频率偏差

频率的实际值与额定值之差的百分数为

(10)

2.2.4 响应速度指标

本文从上升时间、峰值时间、过渡时间、超调量和状态平均持续时间五个指标体现系统动态过程，只介绍超调量和状态平均持续时间.

(1)超调量

最大偏离量h(tp)与终值h(∞)比的百分数为

(11)

(2)状态平均持续时间

(12)

公式中：λk为状态X中第k个分量的跃迁速率.

2.2.5 可靠性指标

(1)总等值停运时间

(13)

公式中：EOTk为一年中第k次停运的等值停运时间.

(2)电量不足期望值

系统供电能力不足导致的负载减少量为

(14)

公式中：FENDS(Xi)为在状态Xi状态下减少的负荷量；N为减少的总量；T为8 760 h

(3)严重程度

系统在峰值负荷期间失去满负荷的时间[13]为

(15)

(4)贡献指数

反映了扰动对系统可靠性的贡献水平，值越大，可靠性越低.

(16)

公式中：EENS0和EENS1分别为扰动发生前后值；CUHV为额定容量.

2.2.6 灵敏度指标

灵敏度是指优化目标对参数变化的敏感度[14].

(1)功率灵敏度

系统受到扰动后，功率对时间变化的敏感度为

(17)

(2)电压灵敏度

系统受到扰动后，电压对时间变化的敏感度为

(18)

(3)电流灵敏度

系统受到扰动后，电流对时间变化的敏感度为

(19)

(4)功角灵敏度

系统受到扰动后，功角对时间变化的敏感度为

(20)

3 反非广延熵评判法

3.1 反非广延熵的定义

Tsallis熵是由Tsallis提出的，它是BGS统计的一个推广，对于描述非扩展系统的统计力学非常有用[15].广义熵形式为

(21)

公式中：0≤p(i)≤1，且q为非广延参数；k为玻尔兹曼常数.由上式可知，当q值固定不变时，随着系统复杂程度(p(i))的增加，Sq也将增大.

为了使Tsallis熵能够更方便地应用于工程实践，这里给出反非广延熵的表达式为

(22)

由公式(22)可知，反非广延熵与Tsallis熵的特征相反，即随着p(i)的提高，S′q将非线性减小，这意味着当以多个评价指标作为依据进行系统评价时，各指标内数值的差异性越大，反非广延熵值越大，这符合系统评价时对各指标熵权的基本要求.

3.2 反非广延熵统计特性

观察公式(22)发现：由于反非广延熵是Tsallis熵的一种变形，所以继承了非广延统计特性，q表征了被测系统的非广延程度.为了深入研究反非广延熵的统计规律，这里以一个二能级系统和一个三能级系统作为研究对象对其进行考察.

设二能级系统由2个独立的子系统A、B组成，根据公式(22)，绘制不同q指数下反非广延熵随p变化关系图(如图3所示，图中p为系统中A子系统的存在概率).由图3可知，在q>0条件下，反非广延熵函数统计特性的变化趋势基本一致，整个函数图象呈现凹状，存在一个极小值；在q<0的情况下，图像呈现凸状，此时只存在极大值.

设三能级系统由3个独立的子系统A、B和C组成时，根据公式(22)，绘制反非广延熵随p和q变化关系图(如图4所示，图中p为系统中A的存在概率，q为反非广延参数).由图4可知，随着q的不断增大，反非广延熵对发生小概率事件的统计能力显著增强，这意味着通过调整q可以改变对被测系统的统计范围并有选择性地提高对不同概率事件的辨识度.

图3 不同q指数下熵随概率分布变化关系图4 反非广延熵随q指数和概率分布变化关系

3.3 评判方法的步骤

随着换流器控制模式及网内潮流的变化，MMC-MTDC输电系统运行状态也将发生相应改变，对运行状态进行准确的判断并实现分级排序，有利于未来实现对交直流混联科学调控，本文提出了一种基于反非广延熵的运行状态分级评判方法，其中综合权重基本上由主观权重和客观权重两方面组成.主观权重由改进层次分析法获得[16].客观权重由反非广延熵权法获得，具体步骤如下：

步骤一：根据改进层次分析法计算主观权重u1(i)

步骤二：计算客观权重

(1)指标归一化

设评估指标数量为m个，有n个状态参与评估，xij为第j个状态指标i的参数，根据以下原则进行指标参数归一化[17]：

对于与运行状态成正比的指标i对应参数按照公式(23)进行归一化

(23)

对于与运行状态成反比的指标i对应参数按照公式(24)进行归一化

(24)

(2)利用公式(22)对HD=[D1，D2，…，Dm]T进行计算；

(3)根据公式(25)确定所有指标的反熵权

(25)

步骤三：综合权重的计算

根据公式(26)组合赋权法确定综合权重：

(26)

设主观权重和客观权重为uk(i)，权重分配系数为k(k=1，2).

步骤四：评价结果

采用线性加权法，将w(i)与各指标参数xij线性加权，得到决策值并进行排序，最终得到评价结果.

基于非广延熵的统计特点，为了满足工程需要，我们提出利用查表法获得恰当q值，这里提出非广延熵的敏感度为

(27)

公式中：Kmax表示S′q(l=1)=S′q(l=2)时对应的K值.

表1 负非广延熵的q取值

当δ=0.33时，我们得到运行状态n(数量)与q的关系，如表1所示.由表1可知，当δ一定时，随着n的增加，q呈上升趋势.

4 仿真验证

4.1 评价指标的构建

将第二节提到的各个指标按顺序进行编号，如表2所示.

表2 指标集及代表含义

4.2 评价结果

基于OPT-5600仿真平台，搭建五端MMC-MTDC系统仿真模型.系统主要参数，如表3所示.设风功率波动(M1)、潮流反转(M2)、风电场侧换流站退出运行(M3)、传统下垂控制下的风功率波动(M4)、改进下垂控制下风功率波动(M5)、传统下垂控制下的潮流反转(M6)、改进下垂控制下潮流反转(M7)、传统下垂控制下风场侧换流器退出运行(M8)、改进下垂控制下风场侧换流器退出运行(M9)9种工况，进行系统仿真，并完成对系统运行数据的采集.数据采集频率为100 kHz，采集的时间为5 s，上述9种工况均发生在1.5 s，持续时间为1 s，q取值为3.7.

表3 主要参数

基于MMC-MTDC输电系统采集到的电压、功率、频率等信号按照第2节的数据处理方法进行归算，得到系统9种不同运行工况的对应指标数据矩阵X31×9.采用提出的评判方法对MMC-MTDC输电系统的运行状态进行评判.首先根据步骤一确定主观权重，然后将表2中指标x1、x2、x9、x10、x11、x12、x16、x17、x18、x23根据公式(23)进行指标数值归一化，其余的指标根据公式(24)归一化，如图5所示.

图5 各指标被归一化后的数值

图6 基于反非广延熵权的评价结果

根据步骤二确定各指标客观权重u2，利用步骤三、四对9种运行状态进行评价，评价结果如图6所示.

通过图6发现，M5的评分最高，而后按照M4、M1、M7、M6、M9、M8、M4、M2的顺序依次降低，M3的评分最低.所以M5的运行状态等级最高，M4、M1、M7、M6、M9、M8、M4、M2的运行状态等级其次，M3的等级最低.

为进一步验证反非广延熵权法的有效性，分别采用IAHP-反非广延熵权法、熵权法和反shannon熵权法对上述9种工况进行评判，其评判结果如图7所示.

根据图7可知，不同方法的排序结果是一致的，但辨识度有所不同.IAHP-反非广延熵权法的分辨率最高，而其余两种方法的评价结果显然没有很好完成对系统低等级运行状态的明确表征.相比之下，采用本文提出的IAHP-反非广延熵权系统运行评判方法的分辨率性和灵活性更高.

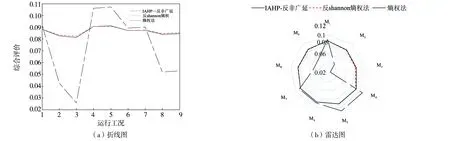
图7 三种方法的评价结果

5 结 论

本文归纳了影响MMC-MTDC输电系统运行状态的主要因素，并构造了对应的指标集，继而提出了一种MMC-MTDC输电系统运行状态分级评判方法，最终得到如下结论：

(1)不同运行工况与控制策略切换会对MMC-MTDC输电系统的运行状态产生影响，本文构建的涵盖功率、电压、频率、系统响应速度、可靠性和灵敏度6个方面的评价指标体系实现了对系统多种特征量的科学分类归纳.

(2)针对现有同类评判方法的局限性，利用反非广熵对小概率事件分辨率高、具有灵活统计特性的特点，提出一种基于反非广延熵权理论的系统性能综合评判方法，实现了对MMC-MTDC输电系统运行状态等级的准确评判.