基于ISSA的STATCOM模型参数解耦辨识研究

王明超，董佳圆，李继影，高磊，聂永辉

(1.东北电力大学电气工程学院，吉林 吉林 132012；2.东北电力大学自动化工程学院，吉林 吉林 132012；3.中广核新能源辽宁分公司，辽宁 沈阳 110000；4.中国电力科学研究院有限公司，北京 100192)

柔性交流输电技术(Flexible AC Transmission System，FACTS)的出现为提升电网可靠性和经济性提供了新的技术手段[3].作为柔性交流输电系统核心器件的静止同步补偿器，能够很好的提高系统的运行稳定性以及电力系统的电压质量，并且STATCOM具有体积小、低电压特性好、响应速度快等一系列优点[1-2].现阶段通过混合仿真或者数字仿真对电网进行分析，首先要保证仿真模型的准确[4].文献[5]使用“开关函数法”建立STATCOM模型，并在模型基础上研究该装置的各项性能.文献[6]通过建立统一标幺值模型，使STATCOM装置级建模问题得到很好的解决.文献[7]将能量方程和输入输出建模方法结合，得到STATCOM输入输出非线性方程模型，在此基础上研究并分析该模型的动态行为.目前针对STATCOM绝大部分的研究主要集中在模型推导建立方面，而在获取准确模型参数、研究参数辨识方法方面却较少.在汽轮机及其调速系统参数辨识中，文献[9～10]使用遗传算法、神经网络等智能算法，取得了较好的效果，但相应存在智能算法迭代寻优时间较长、部分参数辨识不精准等问题.樽海鞘群算法(Salp Swarm Algorithm，SSA)是一种新颖的元启发式算法[11]，与现有其他智能算法相比较，该算法具有简单易行，收敛速度快，计算量小等特点[12].鉴于目前对STATCOM模型参数辨识的研究较少，研究有效的基于樽海鞘群算法的STATCOM模型参数辨识方法具有重要意义.

针对上述问题，本文在现有STATCOM模型基础上，提出改进樽海鞘群(ISSA)算法对STATCOM模型参数进行辨识，针对STATCOM模型同时辨识多个参数辨识结果精度不高问题，提出一种STATCOM双闭环控制模型的dq轴参数解耦辨识策略，建立dq轴解耦待辨识模型，对模型进行分步辨识，仿真结果验证上述方法的准确性.

1 静止同步补偿器模型建立

图1 STATCOM主电路结构

IEEE将静止同步补偿器(STATCOM)定义为向电网提供可控的感性或容性电流从而发出或吸收无功功率的静止电力设备，可将其看做无功功率电源，STATCOM装置的基本电路结构图，如图1所示.L为连接变压器漏抗；R为装置损耗[12].

根据图1得到STATCOM的KVL方程

(1)

式中：i=[iaibic]T，us=[usausbusc]T，uc=[ucaucbucc]T.

(2)

公式(2)转换可写成

(3)

其中：

(4)

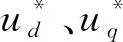
(5)

公式中：Id_ref、Iq_ref分别表示外环电压控制输出的有功电流及无功电流的参考值，结合公式(3)、公式(5)可得到STATCOM电压电流双闭环控制模型及相应的状态空间表达式，如图2所示.

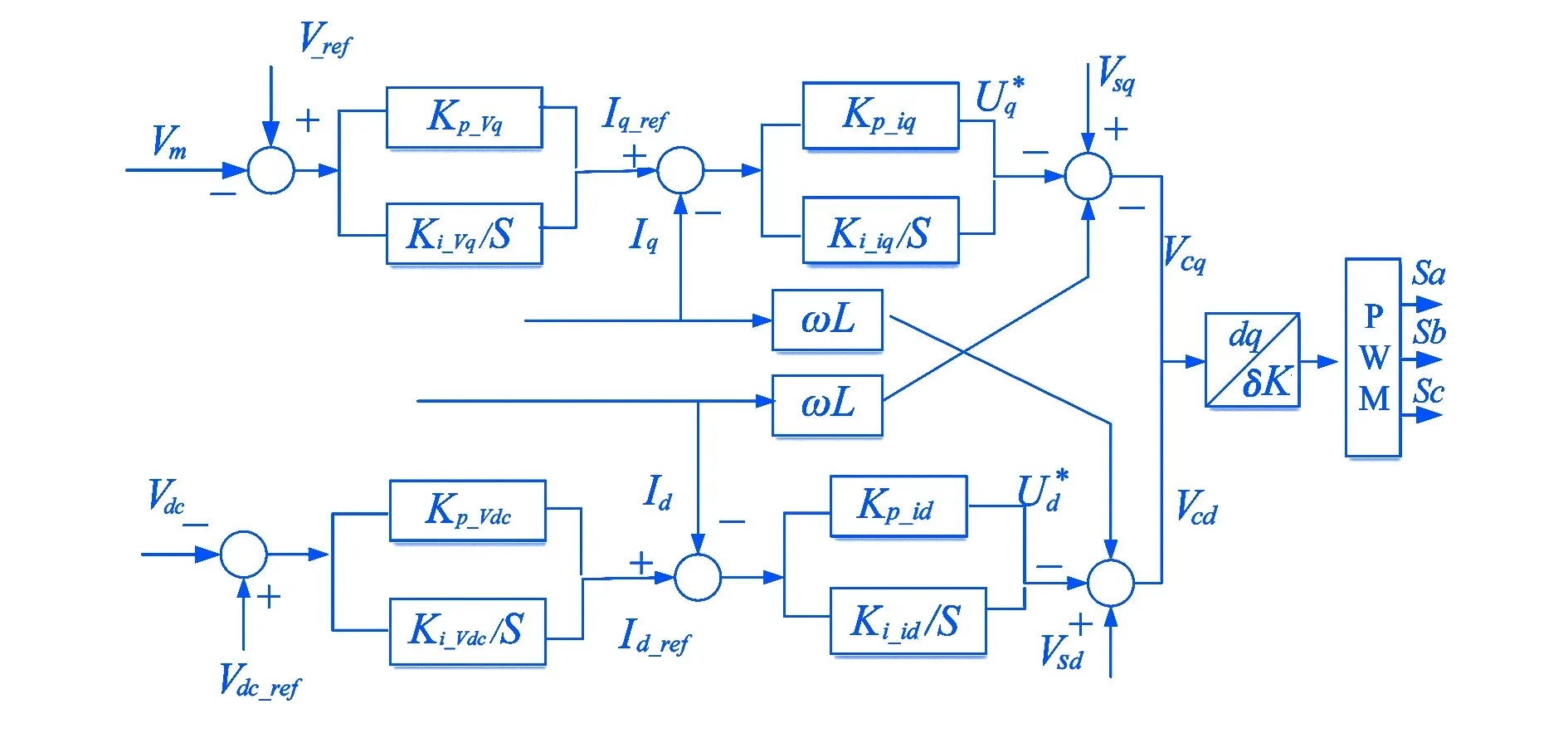
图2 STATCOM电压电流双环控制系统模型

公式中：Vcd、Vcq为双闭环控制输出控制电压dq轴分量；w为频率；Vsd、Vsq为装置接入点三相母线电压的dq轴分量；Id、Iq为经滤波电感后dq轴分量；Kp_id、Ki_id、Kp_iq、Ki_iq分别为电压内环控制的PI参数；Id_ref、Iq_ref为电压外环控制有功电流无功电流参考值；Kp_Vdc、Ki_Vdc、Kp_Vq、Ki_Vq分别为电压外环控制PI参数；L为线路电感；Vm、Vdc为接入点交流母线电压和直流母线电压；Vdc_ref为直流侧参考电压；V_ref为母线参考电压.通过PWM调制得到IGBT的开关控制信号Sa、Sb、Sc.

2 基本樽海鞘群算法

樽海鞘群算法(Salp Swarm Algorithm，SSA)是一种模拟深海樽海鞘移动方式的群智能优化算法[14].其基本思想是模拟樽海鞘的链状移动方式，与其他群体不同的是，位于链前方的领导者以及跟随其后的追随者具有不同的位置更新公式，位于前端的樽海鞘位置更新只会影响到相邻的樽海鞘位置，领导者对排在后面的樽海鞘的影响会逐层锐减，从而使位于链后方的樽海鞘保持良好的多样性[15～17].SSA算法原理简单，具有收敛速度快，计算量小等优点.

整个樽海鞘群分为领导者与追随者两种类型，设置N×D维大小的欧式空间作为算法搜索空间，设搜索樽海鞘群粒子数量为N，一般情况下设置搜索粒子数为30～50之间，D为待辨识的参数个数.空间中存在最优值F=[F1F2…FD]T，樽海鞘位置可表示Xn=[Xn1Xn2…XnD]T.算法搜索的上下界限分别为ub=[ub1，ub2…ubn]，lb=[lb1，lb2…lbn].利用公式(7)初始化樽海鞘群：

XN×D=rand(N，D)×(ub-lb)+lb，

(7)

2.1 领导者更新公式

领导者在樽海鞘群中位于链的首端，在算法迭代寻优过程中负责随机搜索食物位置，对应的位置更新公式为

(8)

(9)

公式中：T为算法最大迭代次数；t为当前算法迭代次数；r2、r3为[0，1]随机数；r3为判断得到的正负决定下次迭代所选用更新公式.

2.2 追随者位置更新

追随者运动方向是跟随链的移动，其本身不具备随机搜索的能力，因此追随者的位置更新公式为

(10)

(11)

3 基于ISSA的STATCOM模型参数解耦辨识方法

3.1 樽海鞘群算法的改进

由追随者位置更新公式可知，追随者在位置更新过程中只是单纯的根据第j-1只樽海鞘的位置信息进行自身位置迭代更新，没有将自身位置与xj-1比较，没有判断xj-1是否优于自身位置，该位置盲目更新方法使得算法的搜索能力受到一定程度的限制.因此，本文引入自适应移动评估策略对原有算法追随者位置更新方式进行改进，解决上述问题.

针对上述问题，提出如下改进以解决追随者盲目追随问题，在进行追随者位置更新时，对第j只和第j-1只樽海鞘的适应度值以及其对应的位置进行优劣判断，根据判断结果决定第j只樽海鞘的位置更新方式，采用式：

(12)

实现这一过程，公式(12)中：c1为学习因子，随迭代进程其值发生变化，c1=(T-t)/T；t、T为当前迭代次数以及最大迭代次数.在算法迭代前期，c1的值较大，使得算法具有较强的搜索能力，能在大范围内搜索食物源；算法迭代后期，c1的取值较小，使得算法在小范围内做仔细搜索，大大提高算法辨识精度.

上述改动，在保留原有种群多样性的基础上，加快了算法的迭代收敛速度，大大减小了算法陷入局部最优导致辨识结果精度较低的可能性.

3.2 基于dq轴解耦的STATCOM模型参数辨识

对STATCOM模型状态公式(6)解析后发现，Vcd中包含q轴的耦合项IqwL，Vcq中包含d轴的耦合项IdwL，两式相互耦合，加大了辨识难度，为此通过引入滤波器方程，对模型做适当简化，减少方程输入量，根据公式(6)，内环电流控制由如下形式表示为

(13)

外环电压控制可以用如下形式

(14)

引入滤波器电路方程为

(15)

结合公式(15)和公式(13)可得

(16)

再将公式(14)带入到公式(16)中，化简可得到两个相互独立的方程：

(17)

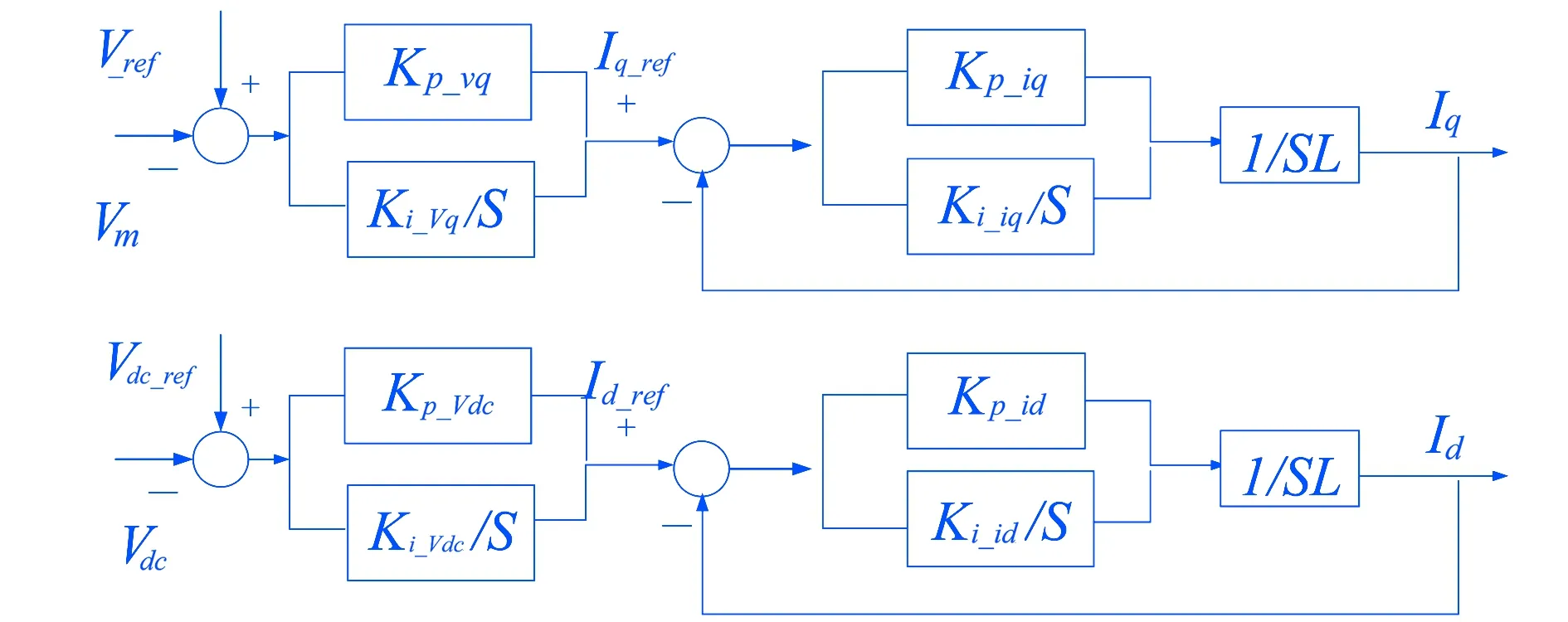
图3 静止同步补偿器dq轴解耦模型

上式实现了dq轴的解耦，两式相互独立，不互相包含耦合项，dq轴实现了互相独立，d轴待辨识参数包括Kp_Vdc，Ki_Vdc，Kp_id，Ki_id，L，q轴待辨识参数包括Kp_vq，Ki_vq，Kp_iq，Ki_iq，L，由公式(17)得到的dq轴待辨识模型如图3所示.

观察图3，参数L在dq轴均可进行辨识，本文将参数L的辨识放在d轴中进行，即首先辨识d轴五个参数，q轴参数保持典型值，在得到d轴参数结果后，将L辨识结果固定，再辨识q轴四个参数，最终得到模型全部9个参数.

3.3 基于ISSA算法的STATCOM模型dq轴参数辨识

STATCOM模型参数辨识实质就是通过优化算法不断产生满足仿真需要的模型参数，通过比较仿真输出与实际系统输出，调整参数搜索范围与方向，最终使得两者误差达到一定精度，输出模型辨识结果.设算法寻优的适应度函数为

(18)

公式中：e(k)为模型仿真输出值与系统输出实际值之间的误差；n为数据长度.

对于d轴模型，设置算法寻优适应度函数为

(19)

对于q轴模型，设置算法寻优适应度函数为

(20)

公式中：id，iq为测量实际系统输出电流dq轴分量；id_cal，iq_cal为辨识后系统输出dq轴分量.

本文主要对STATCOM模型进行整体参数辨识以及分dq轴分参数辨识，通过ISSA算法不断产生随机参数代入仿真模型，由公式(19)、公式(20)判断输出效果优劣，利用ISSA算法调整模型辨识参数，直到满足算法迭代精度或者达到最大迭代次数，最终得到STATCOM模型全部参数辨识结果.

3.4 适用于STATCOM模型dq轴参数辨识的方法流程

综上本文所提出的方法，辨识流程具体如下：

(1)首先辨识d轴参数，根据图3所示dq轴解耦模型辨识d轴参数，待辨识参数为θ=[Kp_Vdc，Ki_Vdc，Kp_id，Ki_id，L]，在1 s时对变量Vdc_ref施加0.05 pu持续阶跃扰动，利用ISSA算法以及仿真输出无功数据对d轴参数进行辨识.

(2)设置算法参数，设樽海鞘群规模大小为N，更新迭代次数为k，最大迭代次数为G，设置搜索上下限分别为ub，lb，并初始化樽海鞘群，规模大小为N×D.

(3)根据公式(19)、公式(20)，计算初始化后的种群适应度值，并将其按大小进行排序，选定食物位置(最优值)为对应排在首位的樽海鞘位置.

图4 STATCOM模型dq轴辨识的总体流程

图5 各算法迭代收敛曲线对比

(4)根据步骤3的排序，将排在首位的樽海鞘设为领导者，根据公式(8)进行位置更新；其他剩余樽海鞘设为追随者，根据公式(11)、公式(12)进行位置更新.

(5)计算更新后的群体的适应度值.将其与食物位置进行比较，选取最优值作为新的食物位置.

(6)对更新后的食物位置进行最优值判断，若该位置达到理论最优值，则将其对应的辨识参数组作为d轴待辨识结果，否则转到步骤4，判断是否达到最大迭代次数，是，则输出结果，否，转到步骤4).

(7)将L固定为d轴辨识结果，辨识q轴参数，ISSA算法辨识步骤同上述步骤2～步骤6.

(8)经两次辨识得到模型全部辨识结果，并根据输出曲线拟合成都验证辨识结果的准确性.

综合上述步骤得到静止同步补偿器控制模型dq轴解耦参数辨识的总体流程如图4所示.

4 仿真算例分析

在MATLAB中搭建两机系统.设置待辨识参数典型值为Kp_vq=5，Ki_vq=100，Kp_Vdc=0.000 1，Ki_Vdc=0.02，Kp_iq=0.3，Ki_iq=10，L=0.22 mH，Kp_id=0.3，Ki_id=10，设置系统在1s时发生阶跃扰动，大小为0.05 pu，得到相应辨识数据，利用辨识智能算法得到辨识.

首先对STATCOM模型参数进行整体辨识，为验证改进樽海鞘算法(ISSA)在辨识参数方面的可行性和优越性.本文利用基本SSA算法、改进SSA算法(ISSA)、基本粒子群算法(PSO)以及差分算法(DE)对模型进行辨识，智能辨识算法迭代次数为20次，分别对各算法得到的平均适应度值以及各参数辨识结果平均值对比.上述各算法分别独立运行20次，种群规模N设为30，算法迭代寻优区间设置为典型值[-30%，+30%].各算法迭代寻优曲线以及相应的辨识结果如表1、图5所示.

表1 四种算法整体辨识结果对比

通过比较表1各算法收敛迭代平均适应度值可得，本文提出的ISSA算法平均适应度值最低为0.037 0，说明该算法辨识结果较其他算法精度最高，由图5各算法收敛迭代曲线可更直观发现，ISSA较其他算法收敛速度更快，在STATCOM模型参数辨识方面具有更大的优势.通过图5可知，PSO算法在整个迭代过程中收敛速度较慢，算法运行时间较长，得到的辨识结果相较其他算法精度较低；DE算法在迭代寻优中容易陷入局部极值，从而导致辨识结果精度有限；ISSA和SSA算法得到的适应度值均远远低于PSO以及DE算法，辨识结果精度更高，并且算法收敛速度更快，相较于SSA算法，ISSA收敛速度更快，性能更优越.通过图6算法辨识结果拟合输出对比曲线可得到：ISSA算法辨识结果曲线相对于其他算法与典型值曲线的曲线拟合效果更好.综上所述，本文提出的ISSA算法相较其他智能算法在STATCOM模型参数辨识方面更加优越性.

图6 0.05 pu扰动下输入电压对比

通过分析表1数据以及图6输出曲线对比，本文提出的ISSA算法在STATCOM模型参数辨识方面相对其他智能算法具有更好的优越性.但通过对表1各参数辨识结果分析发现，即使算法辨识结果拟合曲线与原系统输出曲线拟合效果很好，但部分辨识结果仍存在误差较大的问题.

对此，在利用ISSA算法基础上，采用本文所提出的dq轴解耦辨识策略对STATCOM模型参数进行分步辨识.首先辨识d轴参数，然后固定d轴参数为已知，辨识q轴参数，最终得到仿真模型全部参数，算法设置如下：在1 s时对系统施加0.05 pu阶跃扰动，使用ISSA算法对模型进行参数辨识，算法独立运行计算50次，ISSA算法迭代寻优曲线以及相应的辨识结果如表2、图7、图8所示.

表2 dq轴参数辨识结果

图7 dq轴模型参数辨识收敛曲线

由表2可得，d轴q轴待辨识参数误差均较小，所有参数误差都在5%以内，使用该方法得到的参数精确度更高，由图7可得，使用ISSA算法分dq轴对模型进行辨识，ISSA算法收敛速度很快，收敛精度高，由图8可得分dq轴辨识结果输出曲线与典型值输出曲线基本吻合，从而验证本方法的有效性.

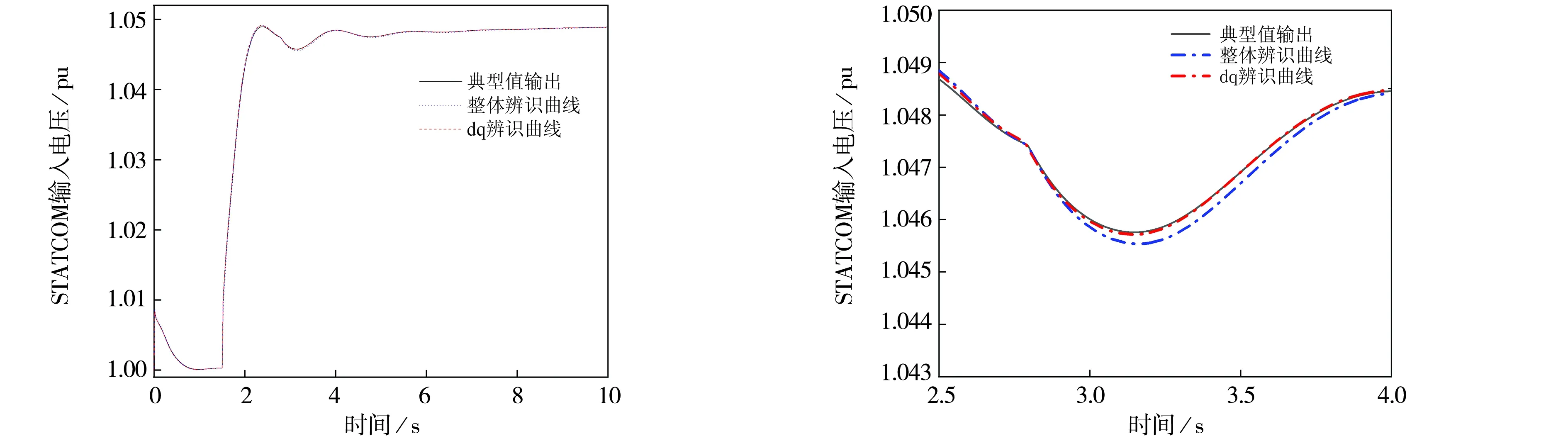
图8 STATCOM输出电压对比

5 结 论

本文以STATCOM模型控制器为研究对象，采用改进樽海鞘群算法对模型参数进行辨识，并提出一种模型参数解耦辨识策略，得到结论如下：

(1)提出一种改进樽海鞘群算法对STATCOM模型参数进行辨识，仿真结果表明该算法收敛速度更快，辨识结果精度很高.

(2)为提高STATCOM参数辨识精度，针对模型结构耦合导致辨识误差较大问题，通过对控制模型状态空间表达式进行化简，提出基于ISSA算法的dq轴解耦参数辨识策略，将整体辨识过程拆分为分dq轴两路辨识，大大提高了参数辨识精度，仿真算例证明所提方法的有效性和准确性.