改进的D-S证据推理地图匹配算法
李昊天,张 宇
(东北电力大学电气工程学院,吉林 吉林 132012)
中国正经历着空前未有的城市化进程,高速的发展将会塑造和定义与之匹配的基础设施,未来会出现更多战略位置上的交通转换枢纽,也会出现更多类似的超复杂路网.目前,很多地图匹配算法都可以较好的解决非复杂道路的匹配问题,特别是近几年出现的一些基于隐马尔可夫模型的地图匹配算法,其匹配准确率基本在90%以上,在某些特定条件下甚至可以接近100%,但在复杂的道路拓扑结构下准确率就会大幅度降低,特别是错综复杂的道路交叉口区域[1-3].
对于该问题,在这种复杂的道路拓扑结构下,使用一些复合的方法进行匹配往往能取得较好的准确率.模糊神经网络的方法主要通过对隶属函数的描述以及界定候选路段的误差模型,该方法的鲁棒性极佳,但计算过于繁琐且缺乏理论根据,实用性不好[4-5].贝叶斯多假设技术根据道路缓冲区域内的候选路段生成伪量测值,并推导出一组假设值,该方法一样可以得到很高的准确率,但由于缺少初始匹配方法,在一定程度上会影响后续的匹配结果[6-7].扩展卡尔曼滤波法是基于卡尔曼滤波中的一种假设,同时考虑系统误差特征,分析经滤波后的系统误差特征能否满足该假设的分布来执行地图匹配,该方法在道路交叉口的稳定性较好,但是没有综合考虑道路拓扑结构和人为因素,因此效果不是很理想[8-9].基于D-S证据理论的算法,首先利用位置与方向信息分别构造基本概率分配函数,再将二者融合为一个新函数,然后比较该函数值的大小,最后选取函数值最大的候选路段作为最佳匹配路段,该方法只考虑两种信息,准确率不是很高[10-11].为了获得更高的匹配精度,适应复杂的道路交叉口,对原有D-S证据推理算法进行改进,并引入一个新的证据——历史匹配程度,综合考虑道路拓扑结构和车辆信息进行地图匹配.当车辆处于十字形交叉路口时,接下来车辆可能会出现直行或者转弯两种行为,如果车辆继续保持直行,那么历史匹配程度证据所占的权重相对较大;如果车辆此时进行左转弯或者右转弯,那么历史匹配程度所占的权重相对较小.当车辆进入T字形交叉路口时,分为两种情况进行分析,第一种情况是车辆接下来可能出现直行或转弯行为,可以根据路面实际禁行情况判断是否引入历史匹配程度作为新的证据进一步提高改进算法的匹配准确率;第二种情况是车辆只能转弯,此时不用考虑历史匹配程度,若该路口禁止左转弯,则匹配结果不会出现错误.通过仿真测试与其他三种算法进行对比,改进算法的单点匹配耗时更少,匹配准确率更高,可以满足道路交叉口的匹配需求.
1 改进方法
1.1 基本概率分配函数
根据D-S证据推理,用样本空间U来表示所有候选道路的集合:U={A1,A2,…,An},设i=1,2,…,n,Ai代表车辆在第i条候选路段上行进.设j=1,2,3,代表第j个证据,用初始定位点P的距离和角度作为D-S证据推理中的两个基本证据,令其函数为ej,i.当j=1时,距离证据函数
(1)
公式中:di为定位点P到该点在第i条路段上投影点的直线距离,该值越小证据越重要.当j=2时,角度证据函数
(2)
公式中:βi为车辆此时行进方向与候选路段方向之间的角度,该值越小证据越重要.根据上述证据公式,构建基本概率分配函数,表示证据j对命题“道路Ai是候选路段”的重要程度,如公式(3)所示.
(3)

图1 算法流程图
1.2 分布式证据融合
改进算法先将距离证据与角度证据进行第一次融合,根据道路拓扑结构判断车辆接下来可能出现的行为,决定是否引入历史匹配程度再进行融合.该融合方式可以减弱人为证据的重要程度,增强客观证据的重要程度,而且当证据数量较少时计算过程相对简单.在地图匹配算法的现实应用中,不规则的真实路段在数字地图中需要借助直线段来模拟,而且每个司机的驾驶习惯不尽相同,导致其经过同一道路交叉口时的行车轨迹也有所差异,因此角度信息证据受人为因素的影响较大,而历史匹配程度和距离作为证据则不易受人为因素影响,所以改进算法中采用该模型,算法流程图如图1所示.
根据D-S证据合成公式,先将之前得到的距离证据和角度证据在样本空间U上的基本概率分配函数m1(Ai)和m2(Ai)融合为一个新的函数m(Ai),表示命题“道路Ai是候选路段”的重要程度为
(4)
公式中:K为冲突因子,表明证据之间互相冲突的程度,K值越小,说明证据之间互相冲突的程度越小.
由于D-S证据推理中的证据过少会致使匹配结果不理想,并且容易导致错误情况的出现,所以改进算法在这里引入了第三个证据——历史匹配程度.首先定义历史匹配程度参数,该值为前一个定位点经过第一次融合后的基本概率分配函数值mp,当j=3时,
(5)
为历史匹配程度证据函数.
将e3,i带入到公式(3)中可以算出历史匹配程度的基本概率分配函数m3(Ai).对各个候选路段而言,历史匹配程度证据的区别在于上一个定位点和当前定位点是否在同一条候选路段上,如果是,那么mp为前一个定位点经过一次融合后的函数值,否则mp=0.
运用该模型继续进行融合,将公式(4)中距离和角度融合得到的函数m(Ai)作为一个新的函数,与历史匹配程度证据的基本概率分配函数m3(Ai)加以融合,得到函数m′(Ai)为
(6)
若K=1,则认为相互融合的证据是完全不兼容的,此时不能利用上述公式进行融合.对于完全冲突的证据而言,重要度高的证据明显更加具有优势,但是冲突产生的起因尚不清楚,也不应该全盘否认重要度低的证据.改进算法对冲突因子K进行赋值处理,并适当降低K值,取值时考虑车辆在路网中的实际位置.由于改进算法主要讨论车辆在道路交叉口区域内的匹配情况,根据历史匹配程度,若车辆出现转弯趋势,令冲突因子K=0.9,反之令冲突因子K=0.8,最后通过计算得出函数值最大的候选路段即为车辆当前行进的路段.
2 仿真测试
首先对算法的单点匹配时间进行仿真分析,分别从不同的道路交叉口共选取60个定位点数据测试算法,四种算法的单点匹配时间对比如图2所示.随着定位点个数的逐渐增加,算法的单点匹配时间几乎都在一定范围内不规则波动,与其他三种算法比较可知,改进算法消耗的时间大致在1 ms~2 ms之间波动,可以满足地图匹配算法对于时效性的需求.
接下来验证改进的D-S证据推理算法在高频采样下的匹配效果,对不同采样时间间隔下的算法匹配准确率进行仿真,其变动规律如图3所示.对于1 s间隔的采样数据,算法具有极佳的匹配准确率,随着时间间隔的不断增加,算法的匹配准确率呈下滑走向,最后渐渐趋于平稳.

图2 单点匹配时间比较图3 匹配准确率与采样间隔的关系曲线
为了进一步验证该算法的匹配精度,分别与上述三种地图匹配算法的精度进行对比,并统计各算法的最低准确率和平均准确率,如表1所示.通过分析未能正确匹配的定位点特征,发现造成错误匹配的原因主要有两个方面:第一是车辆存在绕行的情况,即车辆在行驶过程中两次或多次经过了同一个道路交叉口,导致算法忽略了该部分的候选路段,使得经过融合后的函数值更小;第二可能是真实路网中存在某些路段,但是在电子地图上这些路段没有正确显示出来,在这种情况下,定位点只能强行匹配到更符合的候选路段上,以致造成了错误情况的出现.

表1 匹配准确率对比

图4 算法模拟仿真图
为了验证改进算法的性能,选取吉林市财富广场及其周边区域的复杂道路作为模拟测试路线,这段路线包含十字形和T字形两种道路交叉口,同时设定高频采样的时间间隔为1 s,其定位点匹配仿真模拟的结果如图4所示,车辆的初始位置位于左下角,经纬度坐标为(126.566 4,43.845 5).由于测试道路出现重叠现象,为了便于区分,使用黑色空心圆和蓝色空心圆表示初始定位点,红色空心圆和绿色空心圆表示匹配位置点,由图4可知:改进算法能够较为精准的确定出车辆当前所在的实际位置.
初始定位点序列、匹配点序列以及实际道路选取点序列的经纬度比较,如表2所示.从表2数据可知,匹配点的经纬度和实际道路的经纬度大致相同,只有略微差距,同理可以得出改进算法的性能可以满足道路交叉口的匹配需求.

表2 经纬度比较

(续)表2
车辆行驶过程中经过的道路交叉口示意图,如图5所示.表3~表8分别是选取车辆经过的六个道路交叉口的基本概率分配函数m(Ai)和m′(Ai).通过分析表中数据可以看出,两个证据经过一次融合后的函数值有时相差甚微,不能直接判断出车辆在哪条候选路段上行驶,此时通过引入新的证据进行二次融合比较函数值m′((Ai)的大小,可以确定当前时刻车辆所在的候选路段.综上所述,算法经过两次融合后的匹配准确率有所提升,可以减少错误匹配情况的出现,提高算法性能,满足地图匹配的实际需求.
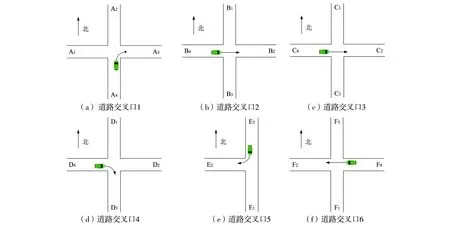
图5 道路交叉口示意图

基本概率分配函数候选路段A1候选路段A2候选路段A3候选路段A4m(Ai)0.42620.09130.41360.0689m'(Ai)0.21030.15940.57750.0528

表4 道路交叉口2融合后的函数结果

表5 道路交叉口3融合后的函数结果

表6 道路交叉口4融合后的函数结果

表7 道路交叉口5融合后的函数结果

表8 道路交叉口6融合后的函数结果
3 结 语
为了适应错综相连的道路交叉口,提高算法整体运行效率,改进算法对基本证据函数进行合理简化,构建基本概率分配函数,在距离信息与角度信息两个证据的基础之上引入第三个证据——历史匹配程度证据.通过仿真实验分析,改进算法的单点匹配时间和匹配准确率均有所增益,可以满足复杂的道路交叉口.
改进算法主要适用于道路交叉口,如果车辆长时间没有经过道路交叉口,可能致使匹配出现错误,难以修正车辆的位置.在后续的研究中,可以综合考虑城市交通规则等限制因素,充分利用道路信息来进行匹配,以摆脱对道路交叉口的依赖,并进一步优化算法整体的性能.

