以教之悦动 促学之实效

卓晓萍

摘要：教学要遵循过程性教学原则，以知识的发生、发展和形成过程为主线，使学生真正参与到发现新知的过程中，经历其中的思维活动，积极主动地参与学习活动.

关键词：高中数学;以生为本;悦动

数学知识结构是由一系列数学概念、公式、定理、性质以及隐藏在概念、公式、定理、性质发生、发展过程中的数学思想、方法构成.数学教学应在学生已有的知识和经验的基础上，设置问题情景，让学生在数学活动中实现经历、体验和探索数学知识的过程并在这个过程中自主构建内在的数学知识体系与发展思维能力.因此数学教学要关注过程性教学，让教学悦动有效，引导学生理解知识方法，提高探索解决问题的能力，真正做到润生细无声.笔者认为让过程性教学悦动有生命力可以从以下几个方面做起：

1 激发学生学习兴趣是教学悦动之源

教师的教学过程和待生态度直接影响到学生的数学学习兴趣.教育家乌申斯基说过：“没有丝毫兴趣的强制性学习，将会扼杀学生探索真理的欲望.”有了兴趣才能更好地点燃学生的学习激情，激发他们的学习潜能，他们就会乐于并主动地去发现问题、提出问题、探索解决问题.例如在“概率”教学中可以举生活实例：“2016年2月28日，勇士对雷霆，库里超远三分绝杀，将比分定格为121∶118”，你能确定神奇的库里在下一场NBA比赛中的超远三分一定能进吗？抓住生活实例中包含数学思维的部分，激发学生的听课热情，从而提高课堂效率.

2 以生为本是教学悦动之根本保证

2.1 结合学生已有认知结构设置合理问题串

在每一个新知产生之前充分了解学生现有的与新知相关的知识体系，根据学生“最近发展区”，设置问题串，步步引导，让学生经历知识形成过程.

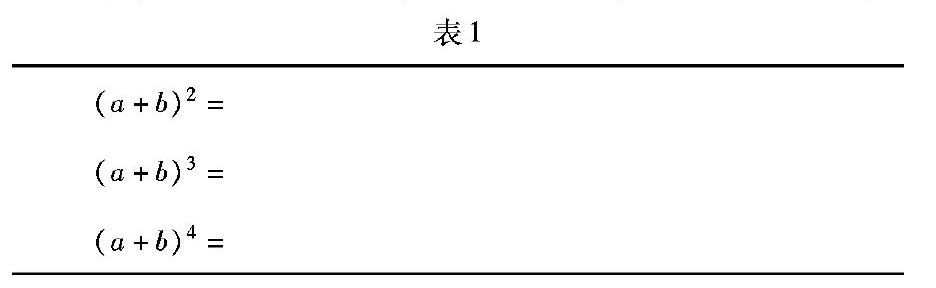
案例1 《二项式定理》片段教学展示（二项式定理的生成过程）：

学生已有的知识背景是多项式乘法的运算法则、组合数的应用、杨辉三角形等;已有的数学能力是：观察、归纳、猜想;已有的数学思想是：简单的化归与转化.

（1）学生分组活动（每小组4人，分工合作完成）

活动效果 观察展开式的特征，学生能较快发现各项的特征并把各项的系数与学生所熟悉的杨辉三角形联系起来，这样学生能很容易可以写出n=5，6时的展开式，但至此还是不能写出（a+b）n的展开式.

（2）师生合作，突破难点

教师引导：

①多项式乘法的运算法则是什么？

②（a+b）3的展开式有几项？

③每一项是如何得到的？

④能否依此分析展开式的各项含义？

⑤（a+b）4的展开式能否用类似的形式来写？

⑥试猜想（a+b）n的展开式.

⑦试类比（a+b）4的展开式的证明过程证明（a+b）n的展开式.

活动效果 在定理的探索过程中，通过教师设问引导，让学生从几个特殊的二项展开式观察规律，联想到杨辉三角形，兴奋之余，思维第一次产生了碰撞，进而渗透化归与转化思想，回归到问题的本质——多项式的乘法问题.进一步引导学生利用计数原理分析展开式各项的系数，类比推广到指数n的情况，推出定理.培养了学生观察、分析、归纳、类比等数学推理素养，体会从特殊到一般的思维方式.学生经历了定理的产生过程，对定理的理解较为深刻，应用时才会更灵活.

2.2 结合学生实践能力设置数学实验

学生亲历知识的产生过程无疑是学习的好途径.一个好的数学实验胜过老师的百句用心叮咛.通过实验、探究，归纳亲历知识的产生过程，深刻体会到知识的来龙去脉，那么对知识的掌握必然是深刻的，亦能达到好的学习效果.高中阶段的数学实验可以借助多媒体、数学教具等辅助教学.

案例2 函数零点存在定理的产生过程.

教具：一根绳子、双面胶、粉笔、直尺.

实验准备：画出坐标系，固定住绳子的两个端点，使得它们分别在x轴的两侧.

实验过程：（1）把图象看作某个函数y=f（x）的图象，改变绳子的形状，观察图象与x轴的交点个数;

（2）调节点（a，f（a））与点（b，f（b））的位置（在x轴同侧或异侧），重复步骤（1）;

（3）剪段绳子，把得到的两段绳子摆成符合函数图象特征的图象，各小组分别完成表格2：

不同的小组实验中所摆出的函数图象不同，但得到的结果是一样的.通过实验，学生得到了零点存在定理，还发现了定理中的关键词：连续不断，f（a）f（b）<0，至少.

2.3 突出思维过程让教学悦动更有实效

案例3 已知a，b，c>0， 且a2+b2=c2，求证：an+bn

思路1 從不等式两边的差异性入手.

（1）观察不等式an+bn

①不等式两边指数n一样;

②不等式左边出现字母a，b，右边消去字母a，b，出现新的字母c.

针对差异作出消除差异的变换：

cn=cn-2c2=cn-2（a2+b2）=cn-2a2+cn-2b2（通过c2=a2+b2消除字母上的差异）.

（2）观察不等式cn-2a2+cn-2b2>an+bn出现了新的差异：

①不等式两边字母指数n不一样;

②不等式左边出现字母a，b，c，右边消去字母c.

针对新的差异再消除：

cn-2a2+cn-2b2>an-2a2+bn-2b2（通过c>a，c>b消除字母和指数上的差异）.

由a，b，c>0 且a2+b2=c2，可以得到 c>a>0，c>b>0.

这样通过两次消除，并积累起来，就完成了解题.

思路2 从条件与结论之间的差异性入手.

观察条件a2+b2=c2与结论an+bn

（1）以条件到结论作为目标方向进行升次消除差异作出变换.

因为an+bn=a2an-2+b2an-2=c2an-2，所以an+b2an-2=c2an-2.

进一步分析an+b2an-2=c2an-2与an+bn

对结论作等价变形an+bn

则an+b2an-2≥an+b2bn-2=an+bn，c2an-2≤c2cn-2=cn，利用不等式传递性得以证明.

（2）以结论到条件作为目标方向消除差异作出变换.

an+bn

（a2）n2+（b2）n2

x+yn=xn+C1nxyn-1+C2nx2yn-2+…+Cknxkyn-k+…+yn得x+yn>xn+yn.

对比新的不等式两边结构特征，应用二项式定理实现证明.

還可以这样变形：

ac2+bc2=1acn+bcn<1.

结合勾股定理进行直观验证，如图4，斜边不变，两直角边变小后三角形为钝角三角形.

思路3 同时对条件和结论作变形，削弱差异.

a2+b2=c2ac2+bc2=1，

an+bn

对比变形后的不等式两边寻找差异：①不等式左边含有字母a，b，c，右边是常数;②不等式左边指数是n，右边是常数.

针对差异作出等价变形：

（1）acn+bcn<1acn+bcn

（2）ac2+bc2>ac2acn-2+bc2bcn-2=acn+bcn（利用0

（3）acn+bcn<1acn+bcn

利用条件消除字母上的差异，实现不等式左右两边具有相同结构，从而构造函数，利用函数单调性证明.

通过分析条件与结论之间的异同，并不断减少目标差来完成解题[1]，让解题过程更加自然，也让学生的解题体验感充满智慧与乐趣.

总之，数学教学要回归数学教育的本来面目，着眼于学生的长期利益，关注过程性教学，关注学生的纵横向发展，注重学生素养的培养，给学生提供思考、动手和感悟的实践，使学生在掌握数学知识的过程中学会思考，成为善于认识问题、解决问题的人才[2].

参考文献：

[1]罗增儒.中学数学的解题与实践[M].广西：广西教育出版社，2015.

[2] 章建跃，陈向兰.数学教育之取势明道优术[J].数学通报，2014，53（10）：1-7+66.

（收稿日期：2019-11-09）