基于Dirac函数原理的箱型梁剪力滞效应分析

周月娥，杨绿峰，李红豫

(1.广西民族大学 建筑工程学院，广西 南宁 530006；2.工程防灾与结构安全教育部重点实验室，广西 南宁 530004；3.桂林理工大学 土木与建筑工程学院，广西 桂林 541004)

0 引言

剪力滞效应是箱型截面普遍存在的一种受力现象，忽略剪力滞效应会使得箱梁结构发生失稳和局部破坏[1]。目前有较多针对剪力滞效应分析的研究方法，其中能量变分法是一种应用比较广泛的解析理论方法。运用能量变分法需要定义箱梁纵向位移函数，现有的方法主要有通过剪力滞函数[2-8]或附加挠度[9-11]来建立箱梁横截面的纵向位移表达式。后者相对来讲是一种比较新的方法，克服了前者在形函数选取和边界条件处理方面存在的困难。但是，这2种方法研究多针对均布荷载作用情况，对集中弯矩作用下求解方法的研究比较少。研究表明除了箱梁截面形式、约束条件之外，荷载类型也影响剪力滞效应。本文提出一种基于狄拉克函数[12]建立集中弯矩作用下箱型梁的总势能泛函方法。采用由狄拉克函数的一阶导数项[13]来关联得到集中弯矩作用下与均布荷载作用下相近的表达式。

本文所提方法需要求解箱梁附加挠度的域内控制微分方程。由于外荷载是在梁上不连续分布的集中弯矩，在荷载作用处需补充一个边界条件控制微分方程才可以求解[14]。因控制微分方程中含有狄拉克函数的一阶导数项，一般的传统求解方法难以处理。本文采用常数变易法[15]，将处理狄拉克函数的问题变成处理其一阶导数的问题，其中对于狄拉克函数一阶导数积分的做法采用文献[16]的方法，从而得到了附加挠度的相关表达式。在此基础上，推导得到反映箱梁剪力滞效应的附加挠度的一般表达式和剪力滞系数。针对文献[5]中的箱型梁算例，进行了应力方面的计算，和文献中的方法进行了比较，然后对剪力滞系数进行了计算，并与基于传统能量变分法得到的剪力滞系数进行比较。结果表明本文所提方法可靠有效并且精度更高，能够有效处理箱型梁集中弯矩作用截面处引起的剪力滞系数突变，更能真实地反映箱梁截面的受力状态。

1 狄拉克函数及其一阶导数性质

狄拉克函数表示在集中的短时间内作用的物理量，有些物理现象需要用这样的函数来描述，如力学中瞬间作用的冲击力。狄拉克函数在数学中的定义是

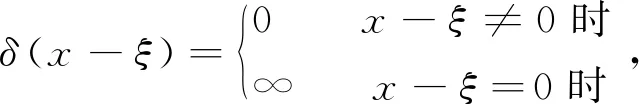
(1)

阶梯函数h(x-ξ)是δ(x-ξ)的一个原函数，有h′(x-ξ)=δ(x-ξ)。定义为

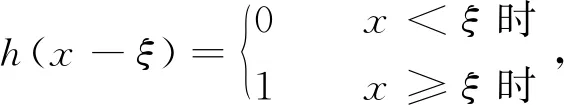
(2)

δ′(x-ξ)表示狄拉克函数的一阶导数，其中狄拉克函数一阶导数积分为

(3)

式中：f(x)是(-∞,+∞)内的任意一个函数。

2 箱型梁的控制微分方程

集中弯矩T作用下的箱型梁及其截面如图1和图2所示。图1中，ξ代表集中弯矩T作用点的位置。图2中，h表示翼缘与截面中性轴(与y轴重合)之间的距离，对应于上、下翼板分别取hu和hb，b1、b2和b3分别表示两腹板之间的上、下翼板宽度之半及悬出翼板的宽度，tu、tb分别表示上、下翼板的厚度，tw表示腹板的厚度，ht表示整个截面的高度。

箱梁的纵向位移函数可以定义为

(4)

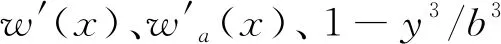
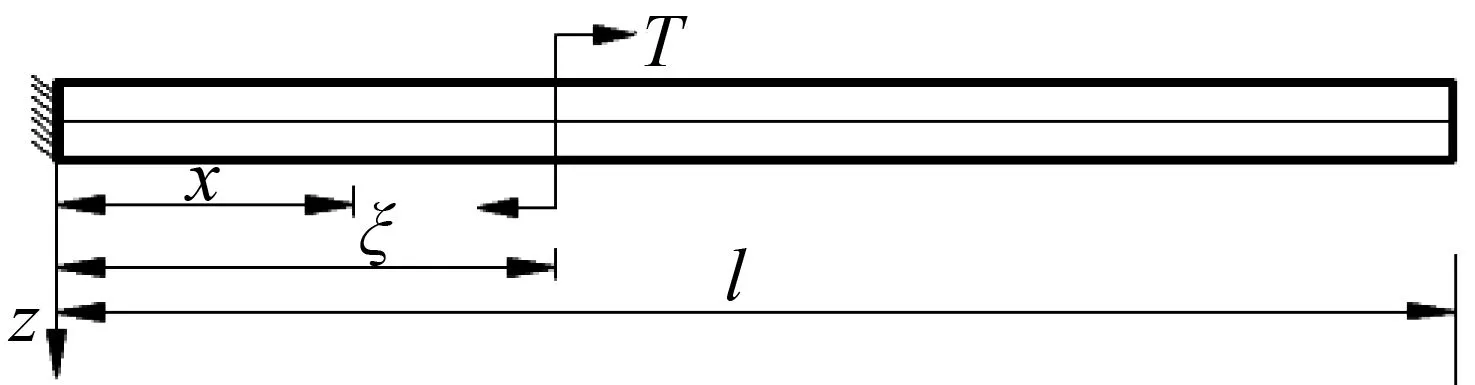
图1 箱型梁承受集中弯矩Fig.1 Box girder under concentrated bending moment

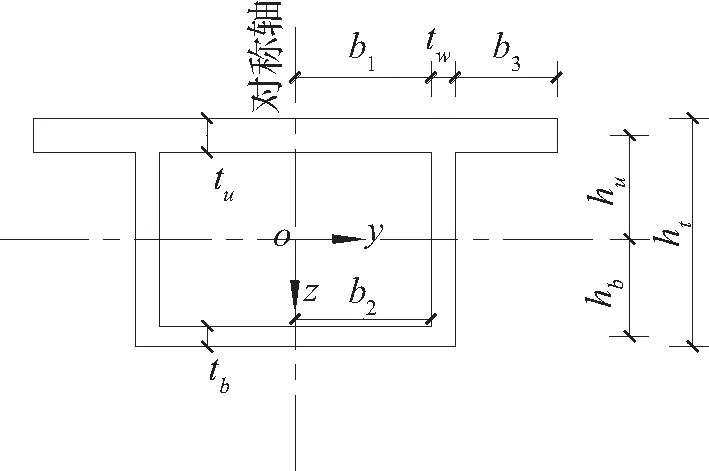
图2 箱型梁横截面尺寸Fig.2 Dimension of cross section

在集中弯矩T作用下，文献[13]中把集中弯矩等效成分布荷载的处理方式如下：

qM=-Tδ′(x-ξ)，

(5)

在此基础上，根据文献[9-10]中的方法得到集中弯矩作用下箱梁的总势能泛函：

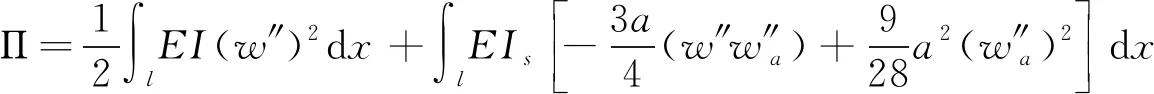
(6)

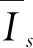
根据最小势能原理，对式(6)求一阶变分，得到箱梁附加挠度和挠度的四阶常微分方程：

(7)

(8)

式中：参数k、n的物理意义见文献[10]，且有

(9)

3 箱型梁的边界条件

式(6)所给出的势能泛函的表达式与文献[9-10]中的泛函表达式近似，区别在于式(6)中的外荷载势能项，边界条件没有发生改变，具体的表达式如下：

(10)

(11)

(12)

(13)

当外荷载作用是集中弯矩时，虽然从数学的角度可以等效成均布荷载来处理，但是实际上荷载是不连续分布的。根据集中弯矩作用处边界条件处理的方法，补充集中弯矩作用点位置x=ξ处的变分条件[14]，有

δwa1(ξ)=δwa2(ξ)=δwa(ξ)，

(14)

δw′a1(ξ)=δw′a2(ξ)=δw′a(ξ)。

(15)

4 求解控制微分方程

将式(5)代入式(7)，得到附加挠度的四阶常微分方程的表达式：

(16)

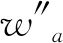
一般形式的微分方程的形式如下：

y″+py′+qy=f(x)。

(17)

根据p2-4q>0,p2-4q=0,p2-4q<0三种情况是要考虑方程(17)对应的齐次方程特征方程根的虚实性。对比方程(16)和(17)可知：p=0，q=-k2，因此有p2-4q=4k2>0，所以直接参考了文献[15]中求解方程(17)的做法来求解方程(16)。

式(17)对应的齐次方程的2个基本解为

(18)

式(17)的通解为y=y1(x)C1(x)+y2(x)C2(x)，利用常数变易法[15]有

(19)

将f(x)=αδ′(x-ξ)代入式(19)得

(20)

(21)

对以上2个式子分别积分可以求得C1(x)和C2(x)的积分表达式，其中对于狄拉克函数一阶导数积分的做法利用式(3)来处理。

得到C1(x)和C2(x)的积分表达式后，继而可以得到式(17)的通解表达式为

(22)

(23)

根据式(2)h(x-ξ)的性质，上式变为

当x<ξ时，

w″a1(x)=C1ekx+C2e-kx=B1shkx+B2chkx，

(24)

当x≥ξ时，

(25)

对式(24)和(25)进行积分和求导处理，可得

当x<ξ时，

(26)

(27)

w‴a1(x)=B1kchkx+B2kshkx，

(28)

当x≥ξ时，

(29)

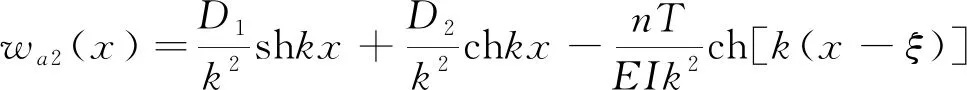
(30)

(31)

5 简支箱型梁剪力滞效应分析

5.1 边界条件及系数确定

简支箱型梁wa(x)的4个边界条件为

(32)

联立式(27)、(30)、(24)、(25)、(14)、(15)求解可得待定系数B1、B2、B3、B4、D1、D2、D3、D4如下：

(33)

5.2 附加挠度及挠度

根据Euler梁理论可以单独确定集中弯矩作用下经典梁挠度wc(x)。其中：

当x<ξ时，

(34)

当x≥ξ时，

(35)

将式(33)中的系数代入式(27)和(30)可以得到附加挠度wa(x)：

当x<ξ时，

(36)

当x≥ξ时，

(37)

最终确定箱梁挠度w(x)=wc(x)+wa(x)。

5.3 应力及剪力滞系数

集中弯矩作用下，箱梁的应力由下式确定：

(38)

剪力滞系数：

(39)

左右简支端，得到挠度和附加挠度的一阶导数后，由下式求剪力滞系数：

(40)

6 算例分析

采用文献[5]中的算例，横截面尺寸有：tu=tb=6 mm，tw=8 mm，ht=80 mm，b1=b2=b3=96 mm，跨长l=80 cm，弹性模量E=3 000 MPa，泊松比μ=0.385，承受集中弯矩M=1000 N·mm。

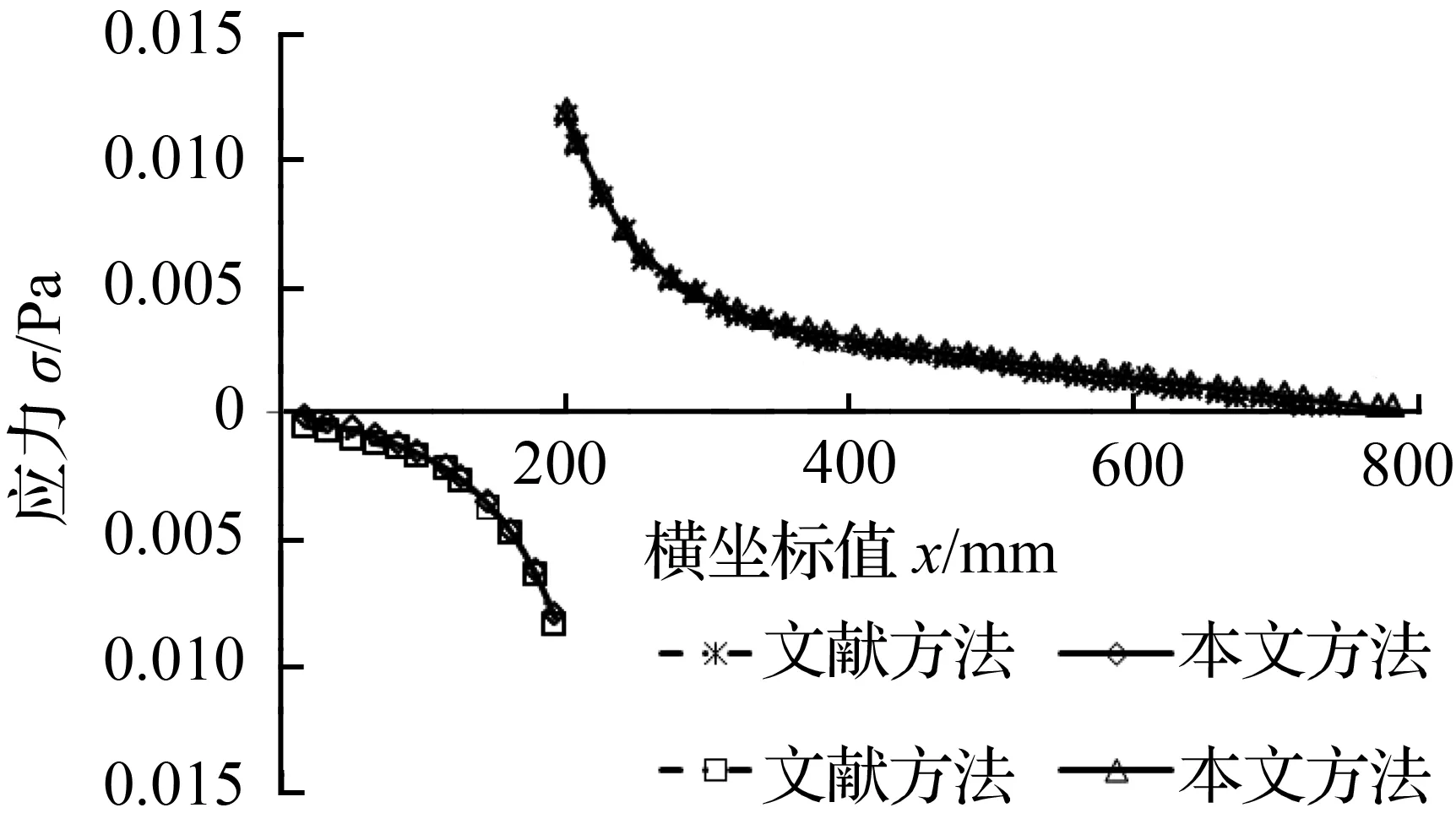
图3 x=20 cm处集中弯矩作用下沿梁长分布的纵向应力Fig.3 Longitudinal stress along the girder length under the concentrated bending moment at the x=20 cm span

当弯矩作用在x=20 cm处时，计算翼板与腹板交界处的正应力，比较本文基于挠度计算应力的方法和文献[5]的计算方法所得结果，如图3所示。从图中可以看出，2种方法计算的应力值吻合较好，而文献中的方法已经与初等梁理论计算结果和有限元数值模拟结果进行了比较，验证了算法的计算精度。因此，可以间接地验证本文方法有以下特点：①利用狄拉克函数的一阶导数将集中弯矩等效成分布荷载是可行的，从而为箱梁在各种外荷载作用下总势能泛函的建立提供了便利；②从附加挠度的角度出发建立的箱型梁纵向位移函数，依此推导出来的集中弯矩作用下箱型梁应力计算公式是可靠有效的。此外，本文方法依然保持了利用外荷载建立总势能泛函中外力势能所具有的优势[10]。

当弯矩作用在x=40 cm处时，沿着跨长计算不同截面处的剪力滞系数，比较本文基于挠度定义的计算方法和文献[5]中基于应力定义的计算方法，结果如图4所示。从图中可以看出，在弯矩作用处左端和右端，基于应力定义的剪力滞系数λσ和基于挠度定义的剪力滞系数λw沿着跨长分别呈现上升和下降的趋势。在弯矩作用处，由于弯矩会发生突变，所以文献[5]方法计算的λσ发生突变，即在x<ξ和x≥ξ情况下推导计算所得到的λσ并不相等。在x=35 cm和x=45 cm处，λσ=2.158 1，开始有发生突变的趋势。而本文方法在弯矩作用处推导计算所得到的剪力滞系数λw的值是比较相近的，没有突变趋势。

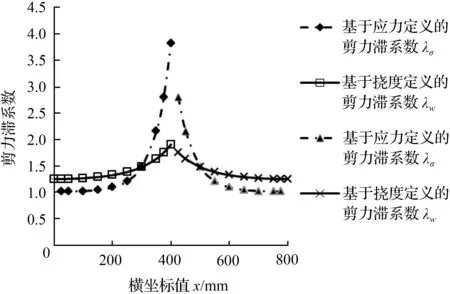
图4 弯矩作用在x=40 cm处的剪力滞系数Fig.4 Shear lag coefficient when load act on x=40 cm

当弯矩作用在x=60 cm处时，计算沿跨长不同截面处的剪力滞系数，比较本文基于挠度定义的计算方法和文献[5]中基于应力定义的计算方法，计算结果如图5所示。从图中可以看出，在x=57.5 cm和x=62.5 cm处，λσ开始有趋于突变的趋势。而本文基于挠度定义的剪力滞系数在x=60 cm左右两端没有突变，x<ξ和x≥ξ情况下推导计算所得到的剪力滞系数λw在弯矩作用处近似相等。

图5 荷载作用在x=60 cm处的剪力滞系数Fig.5 Shear lag coefficient when load act on x=60 cm

7 结论

本文提出基于狄拉克函数建立集中弯矩作用下箱型梁的总势能泛函方法，利用狄拉克函数一阶导数积分的性质推导了附加挠度的一般表达式和剪力滞系数解，获得以下结论：

① 采用狄拉克函数的一阶导数将集中弯矩等效成分布荷载，从而有效地建立了箱梁的总势能泛函，使得泛函的表达式只是跟分布荷载有关的表达式。对泛函求一阶变分得到了附加挠度的常微分方程。采用常数变易法求解含有狄拉克函数一阶导数项的微分方程，关键步骤是要处理好狄拉克函数一阶导数项和函数乘积的积分。

② 通过算例对比分析表明，基于附加挠度定义的应力计算方法与传统的应力计算方法所得结果差别不大，验证了本文基于狄拉克函数的性质得到的剪力滞效应计算方法的准确性。在接近弯矩作用截面处，相较于传统基于应力定义的剪力滞系数有趋于突变增大的趋势，本文所提方法能够有效处理箱型梁集中弯矩作用截面处引起的剪力滞系数突变，更能真实地反映箱梁截面的受力状态。