钢管-焊接空心球节点焊接残余应力数值模拟及试验研究

焦晋峰，贾朋朋，贾玥, 雷宏刚

(太原理工大学 土木工程学院，山西 太原 030024)

0 引言

自20世纪以来，钢管-焊接空心球节点(简称“管-球”节点)平板网架结构因具有高效的受力性能、较好的整体刚度和施工便捷等优点，被广泛应用于带有悬挂吊车的工业厂房中。近年来，随着悬挂吊车吨位的增加，使得网架结构的疲劳问题再次引起工程界的重视[1-2]。国内外统计数据表明，“管-球”节点平板网架结构疲劳破坏常发生在节点焊缝处[2-4]，究其原因，焊接残余应力是导致焊缝处应力集中，加速节点疲劳损伤积累，降低其疲劳寿命的主要原因之一[5-8]。因此，分析和预测焊接残余应力强度及分布规律对优化焊接工艺、降低焊接残余应力，尤其对延长“管-球”节点的疲劳寿命有着重要的意义。

本文以“管-球”节点为研究对象，采用有限元软件ABAQUS焊接接口(AWI)实现对其焊接过程的真实模拟，得到了该节点在焊接过程中的瞬态温度场和应力场以及焊后残余应力的分布规律，并采用盲孔法测量了“管-球”节点试件的焊后残余应力，验证了有限元计算方法的可靠性。

1 管球环焊缝焊接残余应力测量试验

为验证下文焊接残余应力数值模拟结果的准确性，本文采用盲孔法对“管-球”节点焊接残余应力值进行了试验测量。

1.1 试件构造尺寸

焊接空心球和钢管规格根据《空间网格结构技术规程》(JGJ 7—2010)[9]5.2.5条1款规定: 焊接空心球外径与壁厚之比宜取25～45; 空心球外径与主钢管外径之比宜取2.4～3.0；空心球壁厚与主钢管壁厚之比宜取1.5～2.0; 空心球壁厚不宜小于4 mm。考虑到管球材料购买及工厂加工条件等实际因素，节点试件在实际加工制作过程中，对部分零件原设计厚度进行调整，调整后不同零件之间具体关系为空心球壁厚与主钢管壁厚之比为2.5，空心球外径与主钢管外径之比为3.07。本文研究采用的“管-球”节点截面尺寸为空心球规格：外径350 mm，壁厚10 mm,主钢管规格：外径114 mm,壁厚4 mm，节点材质为Q235B钢，如图1所示。

图1 试验试件Fig.1 Test specimen

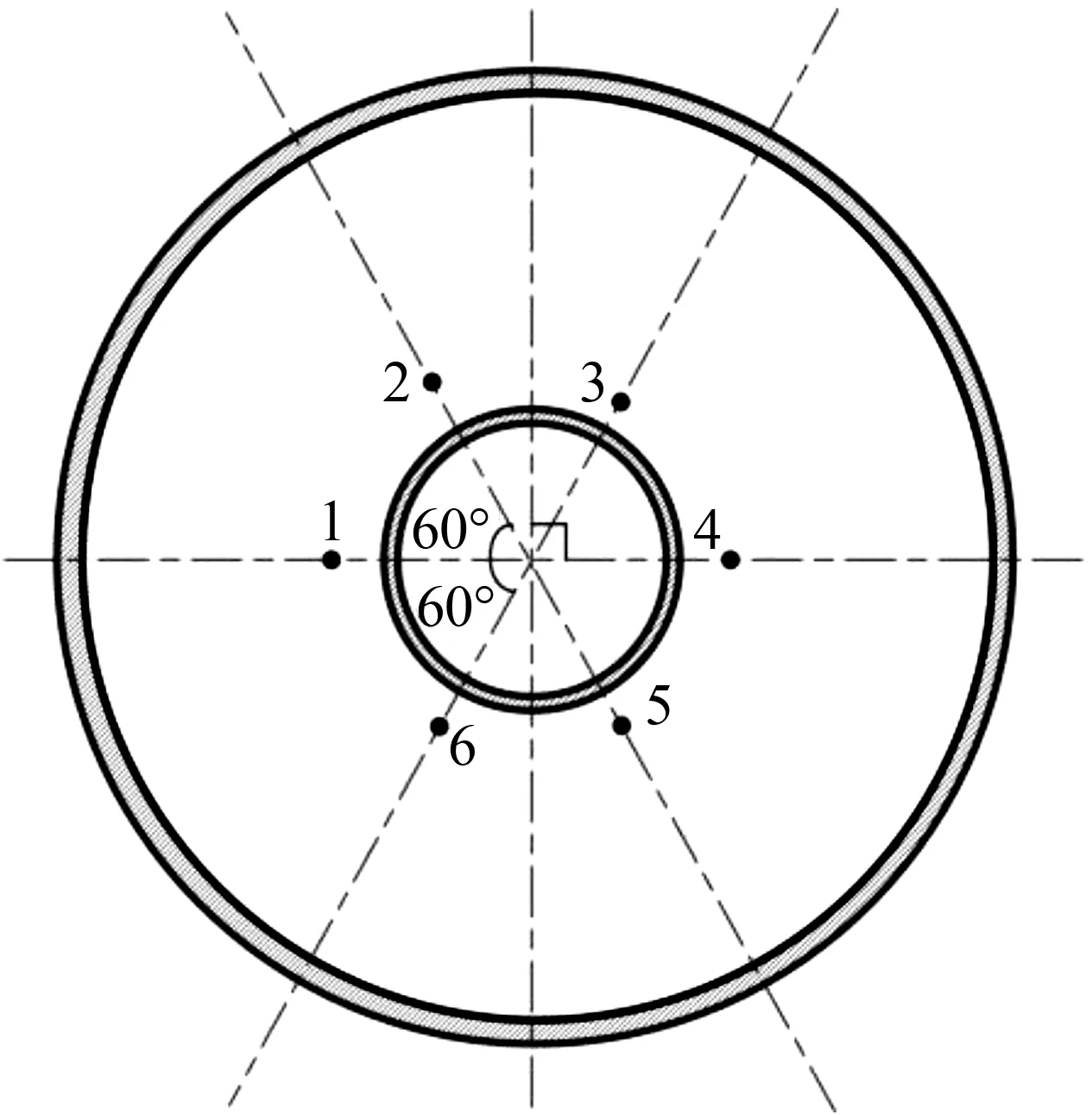
图2 试件测点布置Fig.2 Arrangement of measuring points in specimen

1.2 试验测量装置及测点布置

试验测量装置由2部分组成，分别为钻孔设备和CM-1L-10型静态电阻应变仪。试验测点均布置在焊缝附近的空心球上，为满足《残余应力测量方法 钻孔应变释放法》(GB/T 3395—2013)的测点布置要求，试验测点布置如图2所示，测点1～6距焊趾距离分别为4、4、4、2、3、3 mm。

1.3 试验测量结果

1.3.1 盲孔法简介

盲孔法最早由德国人J.Mathar于1934年提出，经后人的不断改进与完善，目前已成为应用最广泛的测量残余应力的方法，并被美国材料试验协会ASTM标准E837-81所采用。根据《残余应力测量方法 钻孔应变释放法》(GB/T 3395—2013)规定，试验基本步骤为将测点区域打磨光滑，并在测点处黏贴三向应变花，使用钻孔设备在应变花中心打1个直径D约为2 mm、深度为1.2D的小孔(图3)，将测点处的残余应力释放。通过应变仪读取应变花的三向应变ε1、ε2、ε3，再依据公式(1)计算出测点残余应力。

(1)

式中：σ1,2为主应力；ε1、ε2和ε3分别为相应各应变计钻孔后测得的释放应变；A、B为应变释放系数；θ为最大主应力(代数值)方向与应变ε1测量方向之间的夹角，取顺时针方向为正方向。

1.3.2 实验结果

根据《残余应力测量方法 钻孔应变释放法》(GB/T 3395—2013)中8.1.10规定，只要有1个主应力超过材料屈服强度的60 %，需对计算应力进行修正。本文采用应变释放系数分级计算法进行修正，图4为各测点试验测量结果，由于2号测点测得的数据与实际理论严重不符，可将其舍去。

图3 试验盲孔Fig.3 Test blind hole

图4 试验结果与数值模拟对比Fig.4 Comparison of test results with numerical simulation

2 管球环焊缝焊接残余应力数值模拟

2.1 焊接残余应力模拟方法

焊接残余应力数值模拟属于热-结构耦合分析，热-结构耦合分析最简单的方法是进行顺序耦合热应力分析。在这种情况下，首先进行热分析，然后在结构分析中应用热分析结果。使用这种方法，结构性能不影响热结果，符合焊接特性，故本文采用间接顺序耦合分析法对焊接残余应力进行数值模拟。

2.2 有限元模型建立与网格划分

本文采用ABAQUS有限元分析软件建立上述试验“管-球”节点的足尺计算模型，由于该模型具有轴对称的性质，故将模型做1/2简化。考虑到焊缝区和近焊缝区有较大的温度梯度，在焊缝及焊缝附近采用较为精密的网格划分[7]，单元尺寸控制在2 mm以内；在远离焊缝的区域划分相对稀疏的网格，中间设置过渡网格。模型网格划分结果如图5所示，将整个有限元模型离散成101 200个单元，单元类型为传热单元。

2.3 材料属性

焊接温度场模拟属于非线性瞬态热分析，材料非线性对焊接模拟计算结果的准确性会产生重要的影响，但现阶段在高温状态下的材料热物理性能参数相当匮乏，文中材料主要性能参数参考文献[10]并略作修改(见表1)。在焊接过程中，假定对流系数h=25 W/(m2·℃)，部分数据通过线性插值的方法确定。本次模拟考虑了焊料在焊接过程中的固-液相变潜热，将焊缝单元的液化温度设置为1 500 ℃，固化温度为1 400 ℃，潜热值为260 kJ/kg。

表1 Q235B材料热物理性能参数Tab.1 Thermal physical property parameters of Q235B

图6 焊缝截面形状及测点位置Fig.6 Shape of welding seam section and position of measuring point

2.4 焊接温度场数值模拟

“管-球”节点连接采用对接坡口焊缝(图6)，焊接方法采用焊条电弧焊，将焊接温度设置为1 800 ℃，顺时针依次焊接，焊接时间为54 s。

2.4.1 温度场模拟步骤设置

热分析分为以下5步：第1步，将焊缝单元移除；第2步，模拟焊接热源的移动，将热边界条件应用于焊缝与母材的接触面上；第3步，将焊接温度保持一段时间；第4步，将焊缝单元重新激活；第5步，将模型冷却到室温。在焊接过程中，焊接电弧的热输入满足高斯分布。退火温度为900 ℃，冷却时间设置为1 900 s。

2.4.2 温度场模拟结果

温度场随时间变化云图如图7所示。图7(a)为节点在焊接过程中6、36、54 s时的温度场云图，温度最高点出现在焊缝熔池处。由于已焊区表面不断向周围环境散热，温度不断降低，故焊点处比焊后位置等温线密集，其温度梯度也较大。随着焊接的进行，焊池及其附近区域以一个稳定的温度场形态移动，焊缝附近的等温线呈近似椭圆分布。图7(b)为节点在冷却20、200、1 900 s时的温度场云图,图7(b)显示：(1)温度由温度高的位置传向温度低的位置；(2)随着冷却时间的增加，节点温度先急剧降低后缓慢降到室温，并在冷却到1 900 s时，其最高温度降为22.26 ℃，可认为冷却到室温。

6 s

36 s

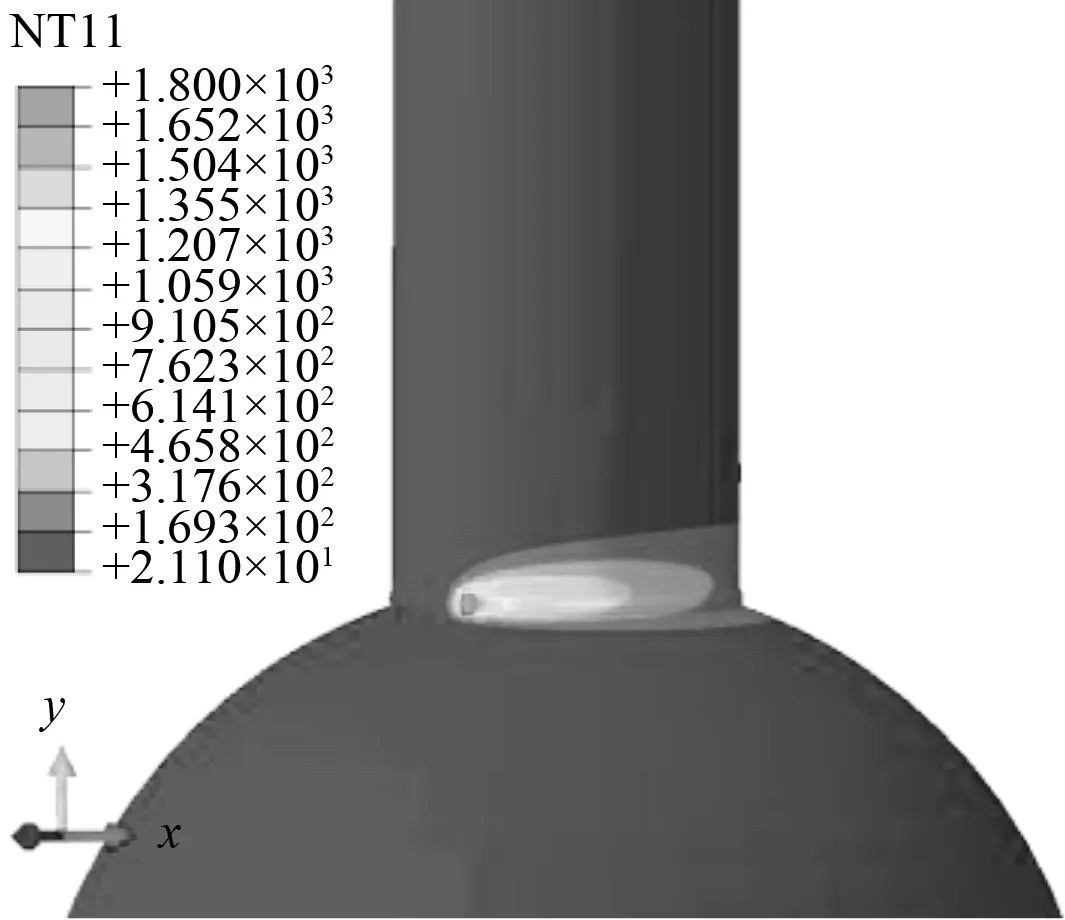
54 s单位：℃

20 s

200 s

1 900 s单位：℃

图8 测点温度时程曲线 Fig.8 Temperature time history curve of measuring point

为研究在焊接过程中焊接温度对节点的影响。本文在主钢管、空心球模型上分别设置了4个测点(图6)，图8为测点温度的时程曲线图。图8表明：(1)在焊接过程中，钢管侧温度约为空心球的2倍；(2)空心球测点1′最高温度与钢管测点3最高温度相近，说明在焊接过程中，钢管侧高于500 ℃的热影响区域约为空心球的3倍。

2.5 焊接应力场有限元分析

2.5.1 应力场模拟设置

在ABAQUS焊接界面(AWI)提交热分析作业的同时，软件自动创建结构模型及荷载步，并以热分析结果为荷载施加到相应的荷载步，所以不必再重新建模，继续采用热分析中的模型和网格形式，使用三维应力单元。故采用顺序耦合热应力分析法对焊接残余应力进行模拟时，热分析与应力分析不能同时提交。

2.5.2 应力场模拟结果

本文选取冷却到室温时的应力作为最终的焊接残余应力，图9为软件完成作业后的Mises等效应力云图。由图9可得：(1)残余应力在焊接接头附近影响区域最大，且对钢管产生了尤为不利的影响，节点其他位置残余应力影响范围较小，主钢管与空心球受其影响区域约为3cm；(2)残余应力最大值出现在主钢管焊缝接头附近处，其数值为282.9 MPa，超过了材料的名义屈服应力。因此，在节点焊接完毕后，需着重对钢管焊缝接头附近位置采取消除残余应力的措施。

(a) 正视图

(b) 后视图单位：MPa

图4为试验残余应力测值与有限元相应测点位置残余应力计算值的比较，除2、4点存在较大误差外，其余各点的有限元模拟结果与试验结果吻合较好，验证了模拟结果的准确性，说明实际的残余应力分布状态可以由有限元软件模拟获取。

2.5.3 残余应力分布模型

为了更好分析残余应力场在节点上的分布，本文结合温度场模拟结果将残余应力场划分为3个区域(图9)，各区域大致范围见表2。

表2 各区域大致范围Tab.2 Approximate range of each region

图10 应力场测点布置Fig.10 Stress field measurement point arrangement

第1区域在焊接过程中经历了2次高温影响，导致此区域应力场分布最为复杂。同时，其残余应力值普遍高于其他2个区域，是残余应力最大值所在的区域。在此区域中，钢管在轴向方向上受残余应力影响尤为严重，在距焊趾45 mm范围内，钢管表面存在高于70 MPa的残余应力。第2区域残余应力值小于其他2个区域，其原因为此区域温度场尚未稳定，受温度场影响较小。第3区域在环形方向上范围远远大于其他2个区域，此区域具有稳定的温度场，故其残余应力云图比其他2个区域有规律。

通过划分区域法，可以很好地解释残余应力的成因与分布规律，因此，可将环形焊缝划分为不同的区域来研究。

为研究第3区域中主钢管与空心球上的残余应力分布规律，在此区域中的“管-球”节点上均匀设置4组测点，每组测点均在同一截面，每组测点所在截面的夹角θ为45°，并将第1个点选取在距焊趾2 mm处(图10)。为了直观地表达主钢管及空心球上的应力分布状态，分别将节点上的每组测点结果绘制成散点图，如图11所示。

(a) 空心球应力测点散点图

(b) 主钢管应力测点散点图

由图11可知：(1)钢管残余应力在轴向方向上的变化趋势：在距焊趾10 mm范围内，应力数值下降平缓，在10～30 mm范围内，随距焊趾距离的增加，应力呈指数形式下降。(2)空心球残余应力在径向方向上的变化趋势为：在距焊趾12 mm范围内，残余应力值先降低后增高，约在距焊趾6 mm处，取到最小值约为110 MPa;在12～30 mm范围内，残余应力值下降平缓。(3)在焊趾处，主钢管焊接残余应力值高于空心球，但在距焊趾12 mm以外范围，主钢管焊接残余应力值低于空心球。

通过对主钢管测点散点图的曲线拟合，本文建立了在第3区域中主钢管焊接残余应力与距焊趾位置的数学模型如图11(b)，公式如下：

(2)

式中:σ1、σ2为等效残余应力，d2为距焊趾位置。第1段函数相关系数为0.874，第2段函数相关系数为0.989，说明公式(2)可以很好地表达主钢管残余应力与距焊趾位置的函数关系。

3 结论

① 本文采用盲孔法测量“管-球”节点焊后残余应力，得到了测点处应力值，验证了焊接残余应力数值模拟结果的可靠性,说明“管-球”节点焊接残余应力分布状况可以由数值模拟获得。

② 在焊接过程中，主钢管侧高于500 ℃的热影响区域约为空心球的3倍，且主钢管侧受热区域温度约为空心球的2倍。

③ 结合温度场模拟结果，可将焊接残余应力场划分为3个区域，并解释了各区域残余应力的特点及成因，提出了通过区域划分来研究环形焊缝残余应力分布的方法。

④ 在第3区域，钢管焊接残余应力最大值高于空心球，并分析得到了残余应力在钢管轴向方向及空心球径向方向上的变化趋势。

⑤ 本文建立了钢管在第3区域距焊趾30 mm范围内残余应力值与距焊趾位置的数学模型，为“管-球”节点焊接残余应力的研究提供参考。