网孔尺寸影响格栅-道砟界面特性的离散元研究

贾亚飞，李升伟，苗晨曦*,3,李杰

(1.太原理工大学 土木工程学院，山西 太原 030000；2.上海市政工程设计研究总院集团第七设计院有限公司，上海 200000;3.山西省交通科技研发有限公司，山西 太原 030000)

0 引言

随着我国有砟铁路建设的现代化程度显著提高，铁路运输趋向于重载化、高速化，从而对有砟道床承载能力和系统性提出了更高的要求。土工格栅作为一种改善散体材料嵌固能力的工程补强措施已被应用于提高铁路有砟道床力学性能上[1]。国内外学者针对散体粒料土工加筋机理以及筋-土界面力学特性的研究工作也取得了一系列有价值的研究成果。邵帅等[2]提出了一种可用于分析土工格栅与道砟颗粒间相互作用的离散元-有限元耦合方法，通过加筋后道砟颗粒的直剪试验研究了土工格栅影响道砟颗粒间的自锁作用内在机理，研究成果可为进一步理解土工格栅的加固机理打下基础。高亮等[3]基于离散元法采用自编算法建立了能模拟真实道砟外形的颗粒簇(clump颗粒)，通过对接触力、配位数、道床应力和振动加速度的对比分析，研究了道床整体受力特性。研究表明颗粒簇能反映道砟间的咬合作用。TUTUMLUER等[4]基于块体离散元法建立的三维道砟颗粒模型，研究了筋材网孔结构对加筋道砟剪切强度的影响，研究成果为从细观角度探究加筋道床作用机制提供了参考。HUSSAINI等[5]借助先进量测元件，通过大型循环荷载试验的开展，系统分析了格栅对碎石道砟的加固效果。研究结果表明，筋材引入能有效约束道砟颗粒横向位移，同时，筋材的存在有利于路基土上部的应力扩散。

总结关于散体粒料加筋效果影响因素的现有研究成果发现，筋材网孔尺寸与填料粒径比值、筋材表面上覆压力、肋条横截面形式、节点强度等因素均影响着加筋体系工作性能[6-7]。当前的研究工作所涉及的影响因素多局限于改变筋材或填料的某一属性上，而值得关注的是，筋材网孔与填料间尺寸关系的协调正是网孔-填料间嵌固作用发挥的关键[8]。在加筋道砟的实际应用中，往往指定道砟级配结构，这时对格栅网孔尺寸的选择就变得尤为重要。为了进一步探究筋材网孔和级配道砟间最优尺寸关系，本文在MIAO等[7]数值模型模拟结果的基础上，对考虑道砟级配结构的格栅加筋道砟拉拔试验进行数值仿真，并基于拉拔阻力变化、筋材轴力分布及格栅肋条变形情况对不同网孔尺寸下双向土工格栅加筋道砟的筋-土界面细观特性进行对比分析。以工程中广泛应用的界面强度指标为标准，从细观尺度上对比不同网孔尺寸格栅的加筋效果。

1 颗粒流拉拔数值试验

1.1 填料、格栅建模方法及参数选取

NGO等[9]通过一系列室内剪切试验、格栅拉伸试验及数值试验，统一标定出了接触刚度模型下道砟颗粒和双向土工格栅的细观参数。除颗粒几何形态与网孔尺寸不同外，本文沿用其主要标定成果。

如表1所示，设计8种不同网孔尺寸的工况进行拉拔数值模拟，其中工况8为无横肋对照组(单向土工格栅)。本文涉及的双向土工格栅节点与文献[6]中三向土工格栅节点突起建模方法基本一致，在节点细部构造方面，采用3颗粒“clump”单元较真实地还原了格栅节点的几何形状，2副颗粒相切于主颗粒球心处。须要指出的是，从属于不同主颗粒的各副颗粒之间并没有接触形成，作用于节点突起部分的外力将传递至其从属的主颗粒上，且副颗粒的引入不影响主颗粒间的接触关系，因此，格栅细观参数仍沿用文献[9]中关于平行黏结的相关标定成果。

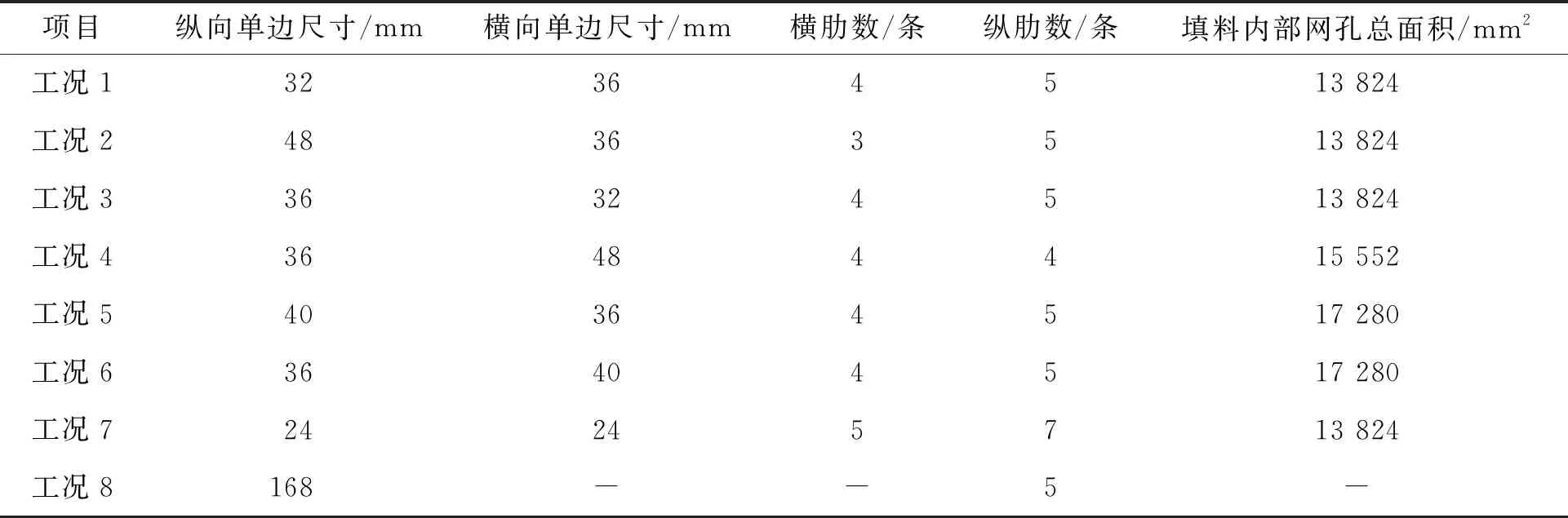
表1 格栅网孔尺寸Tab.1 Sizes of Rectangular Aperture

图1 道砟颗粒级配 Fig.1 Ballast particle grading

道砟颗粒级配如图1所示，为充分考虑道砟颗粒的棱角特征和空间定向随机性，本文道砟颗粒模型采用文献[7]开发的类三角形颗粒，其构造特征在于，由初始纯圆颗粒转换成类三角形“clump”颗粒，转换过程遵循“体积相等、质量相等、重心不变、颗粒长轴定向随机”的原则。子颗粒粒径相同、两两相割且球心连线共面(图2)。

1.2 数值模拟步骤

以工况1格栅尺寸为例，试验布置如图3所示，拉拔试验数值模型加载箱尺寸为300 mm×300 mm×400 mm(x×y×z)，格栅沿模型横向对称布置。拉拔过程中引入伺服机制，通过对上下墙位置的动态调整实现对法向应力的精确控制(图3)。

数值试样生成及拉拔试验步骤简述如下：(1)采用“clump”颗粒逐个替代初始纯圆颗粒，循环消散不平衡力至指定水平；(2)以拉拔通道为界限将加载箱分为上下两部分，分别引入相互独立的伺服加载系统对两部分试样进行预压缩后在拉拔通道生成双向土工格栅；(3)删除多余墙体，重新定义伺服加载机制以控制法向应力。统一计算时步至稳定步长以下，设置过程记录参量，清零颗粒位移信息准备开始试验；(4)施加恒定速度场至格栅纵向边缘5颗粒处，如图2所示。

相关领域的国内外学者通过大量的室内试验和数值模拟试验从格栅应力分布、颗粒体系接触力系演化、筋土界面位移场等宏、细观角度论证了三维离散元模型在研究土工格栅加筋散体粒料方面的适用性及合理性[9-13]。本文在模型宏细观参数取值、道砟颗粒几何形状、土工格栅组成形式及拉拔试验数值实现等方面综合借鉴了前人的研究成果，仅根据试验布置调整了格栅网孔尺寸，限于篇幅，本文不再设置独立章节进行模型合理性论证。

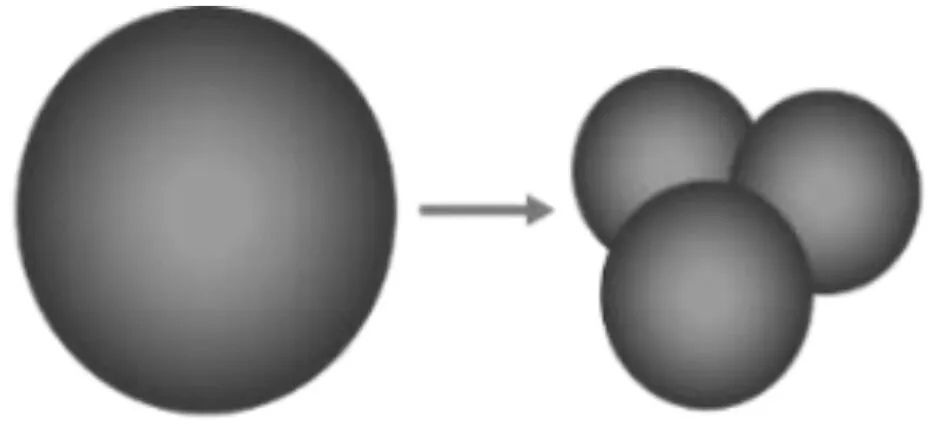
(a) 道砟颗粒转换三维实体图

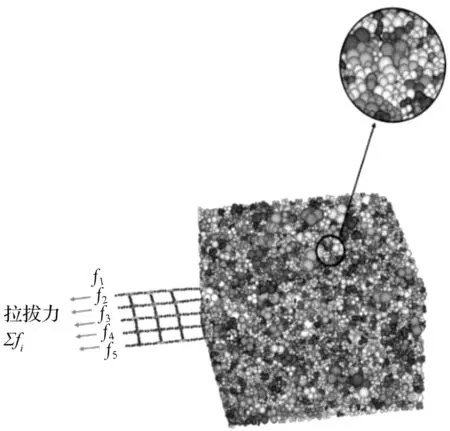
(b) 数值模型中拉拔力示意图

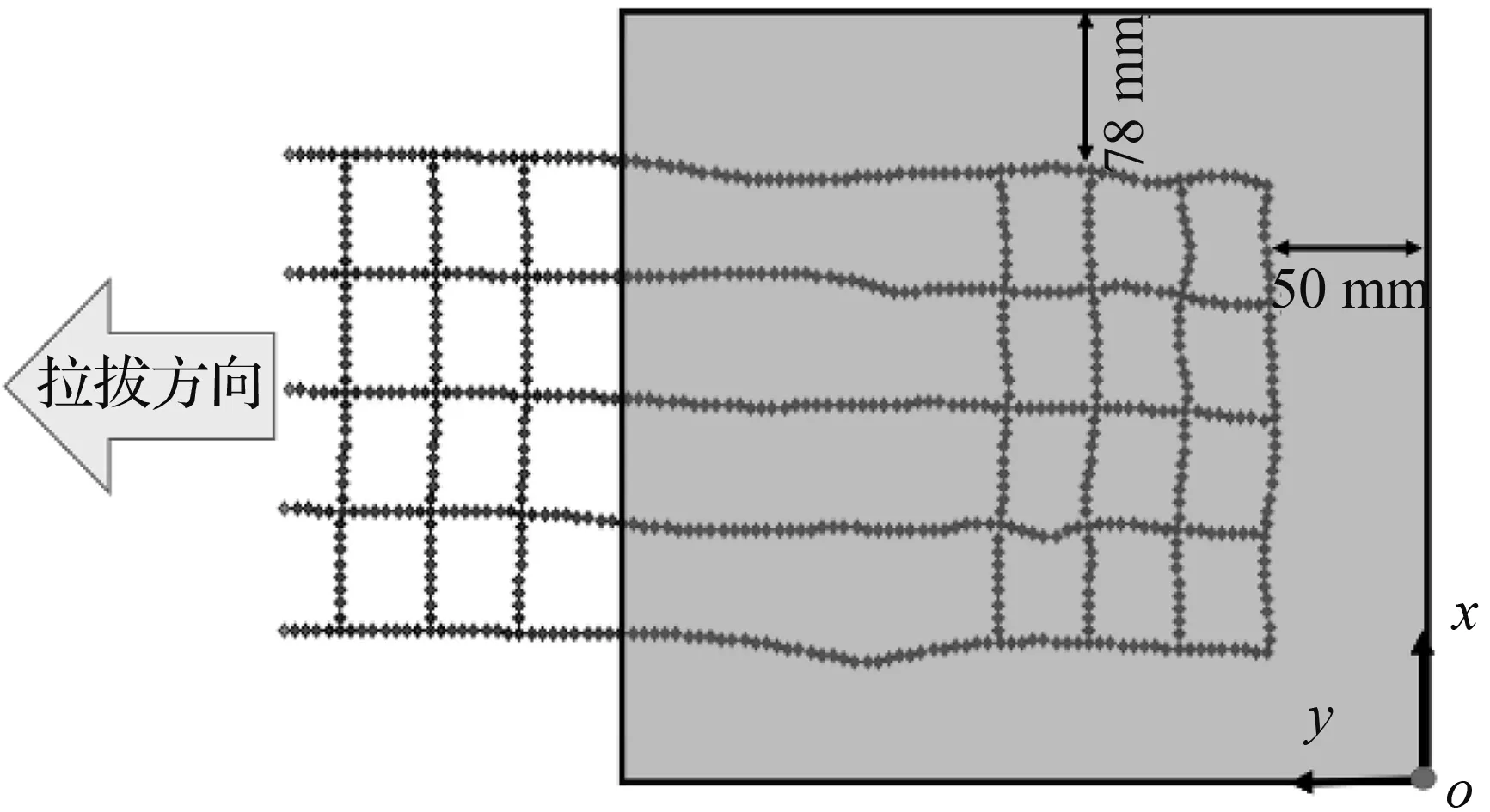
(a) 加载装置布置图

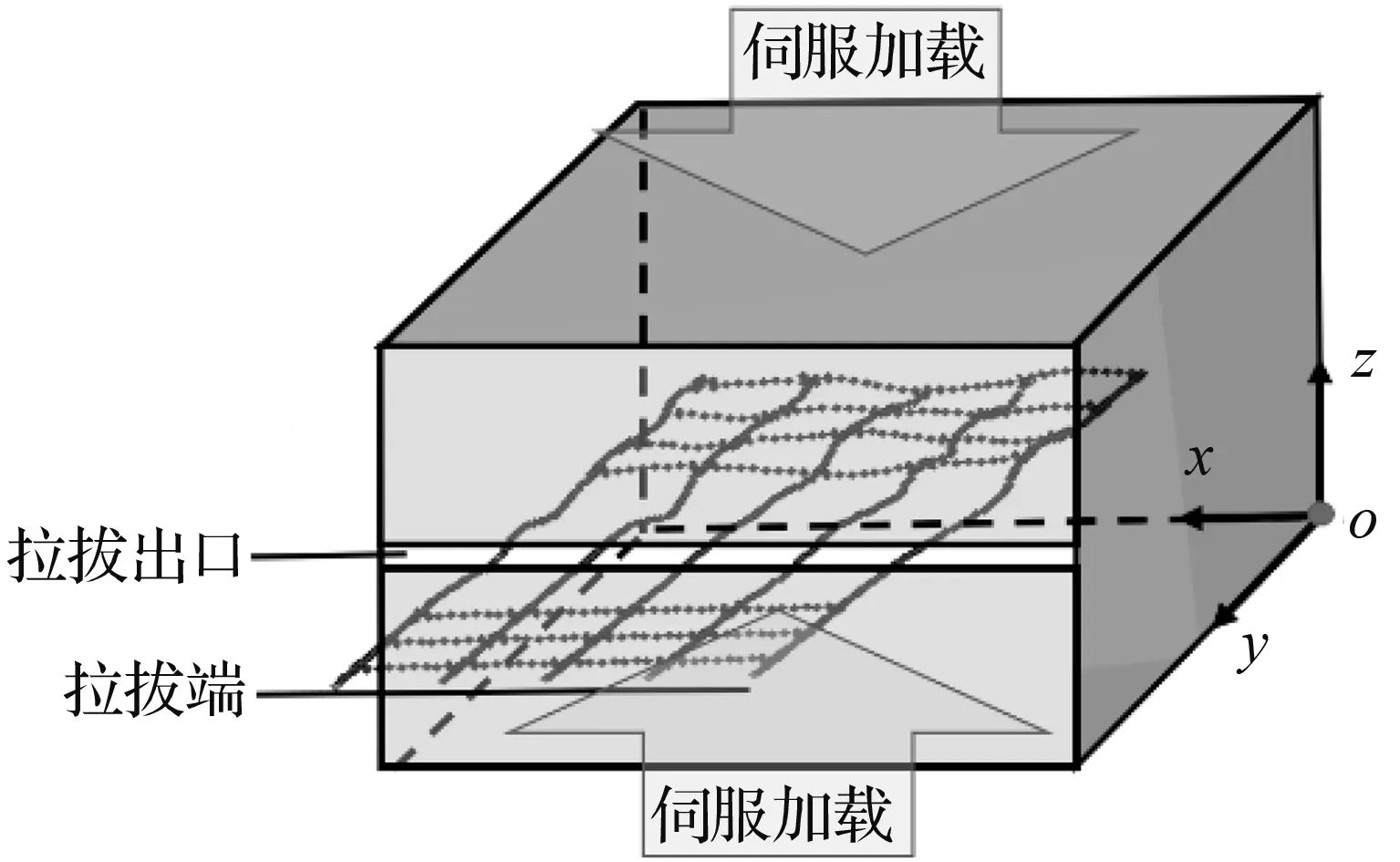
(b) 格栅布置俯视图

2 试验结果细观分析

2.1 格栅拉拔力变化规律

图4为各工况下拉拔力-拉拔位移关系曲线，除工况8(无横肋组)外，在拉拔初始阶段(拉拔位移<10 mm)，各工况下拉拔力发展几乎同步，从拉拔力峰值来看，各工况峰值拉拔力均随法向压力的增大而增加，各级法向应力下拉拔力整体发展趋势与STAHL等[14]和郑俊杰等[15]的研究成果基本一致。在填料内部格栅网孔总面积相同(13 824 mm2)的情况下[图4(a)]，工况3在高法向应力(40、50 kPa)下拉拔力峰值显著高于工况1，而在低法向应力(20、30 kPa)下二者峰值近乎同一水平。这是由于低法向应力下格栅拉拔阻力主要为摩擦阻力，高法向应力下格栅与填料间嵌固作用更加明显，承载阻力为格栅拉拔阻力的主要来源，而横肋尺寸的差异造成了网孔横向收缩程度不同，进而影响格栅-道砟的嵌固效果，宏观上表现为峰值拉拔力的不同。而图4(d)中工况8在各级法向应力下的拉拔力峰值及其对应的位移均远小于其他工况，且峰值后的拉拔力波动幅度相对较小。这也充分说明了横肋是影响格栅-填料间嵌固作用的关键因素。

对比工况2与工况4拉拔力发展规律[图4(b)]，发现工况2在同级法向压力下峰值之前的拉拔力随拉拔位移的增长速率较高。分析其原因，工况4与工况2的格栅单孔尺寸均为相同面积的矩形，拉拔方向的改变导致其纵、横肋互换，随着拉拔进程的发展，在相同拉拔位移下纵肋较短的格栅对填料内部(y轴负方向)逐条横肋的调动要早于纵肋较长者，尤其是在高法向应力下表现得更为明显。而图4(c)中工况5与工况6的网孔更接近正方形，纵、横肋互换后二者的拉拔力发展并无明显变化。

这也说明了纵肋长度的变化对拉拔进程中横肋调动有一定的影响，各工况拉拔力变化规律不仅反映了合理选择格栅网孔尺寸的重要性，同时也进一步说明了分析网孔尺寸对格栅加筋性能影响的必要性。

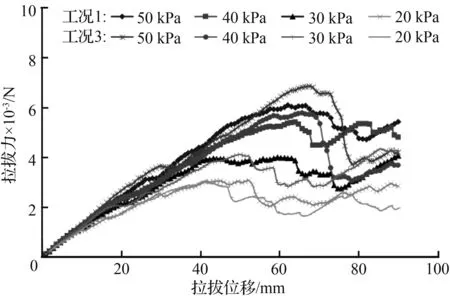
(a) 工况1与工况3

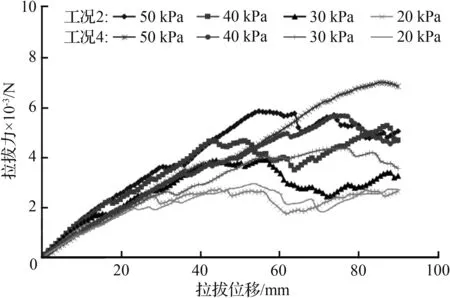
(b) 工况2与工况4

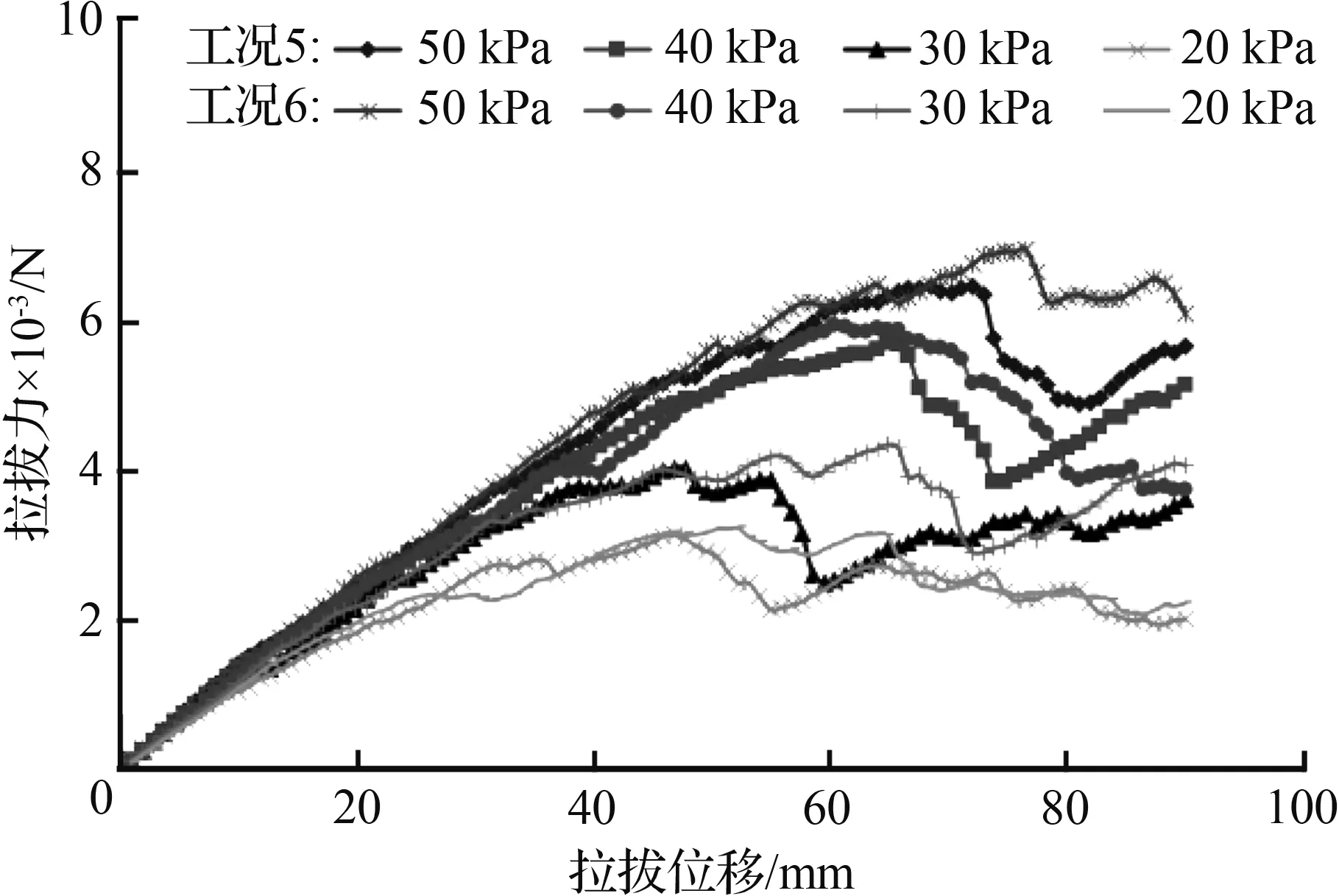
(c) 工况5与工况6

(d) 工况7与工况8

2.2 筋材轴力分布及肋条变形

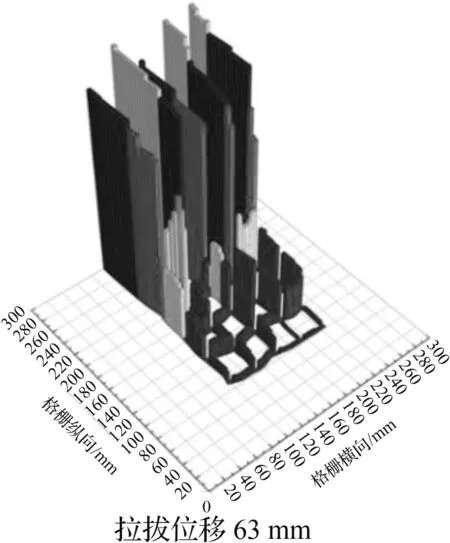
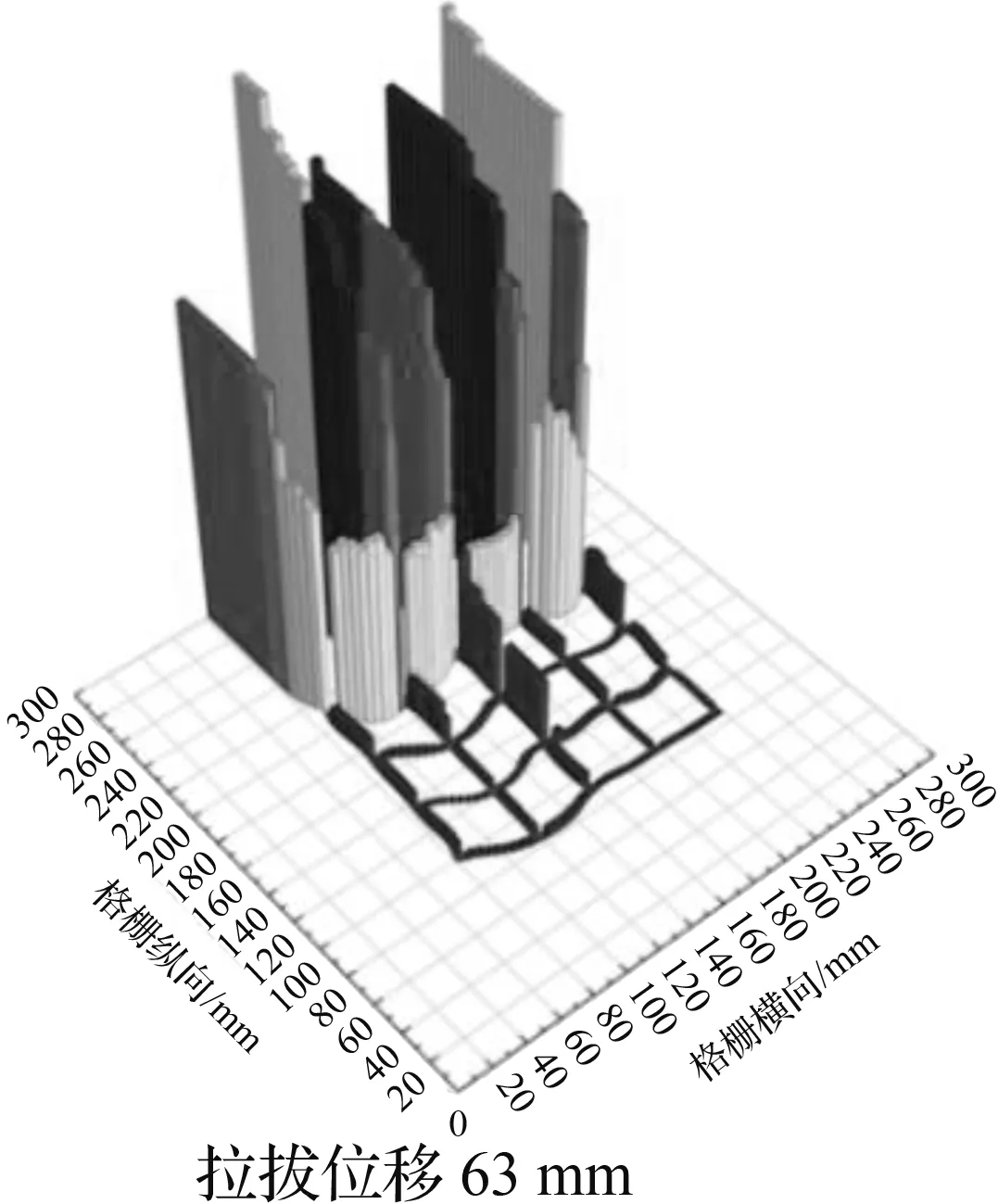
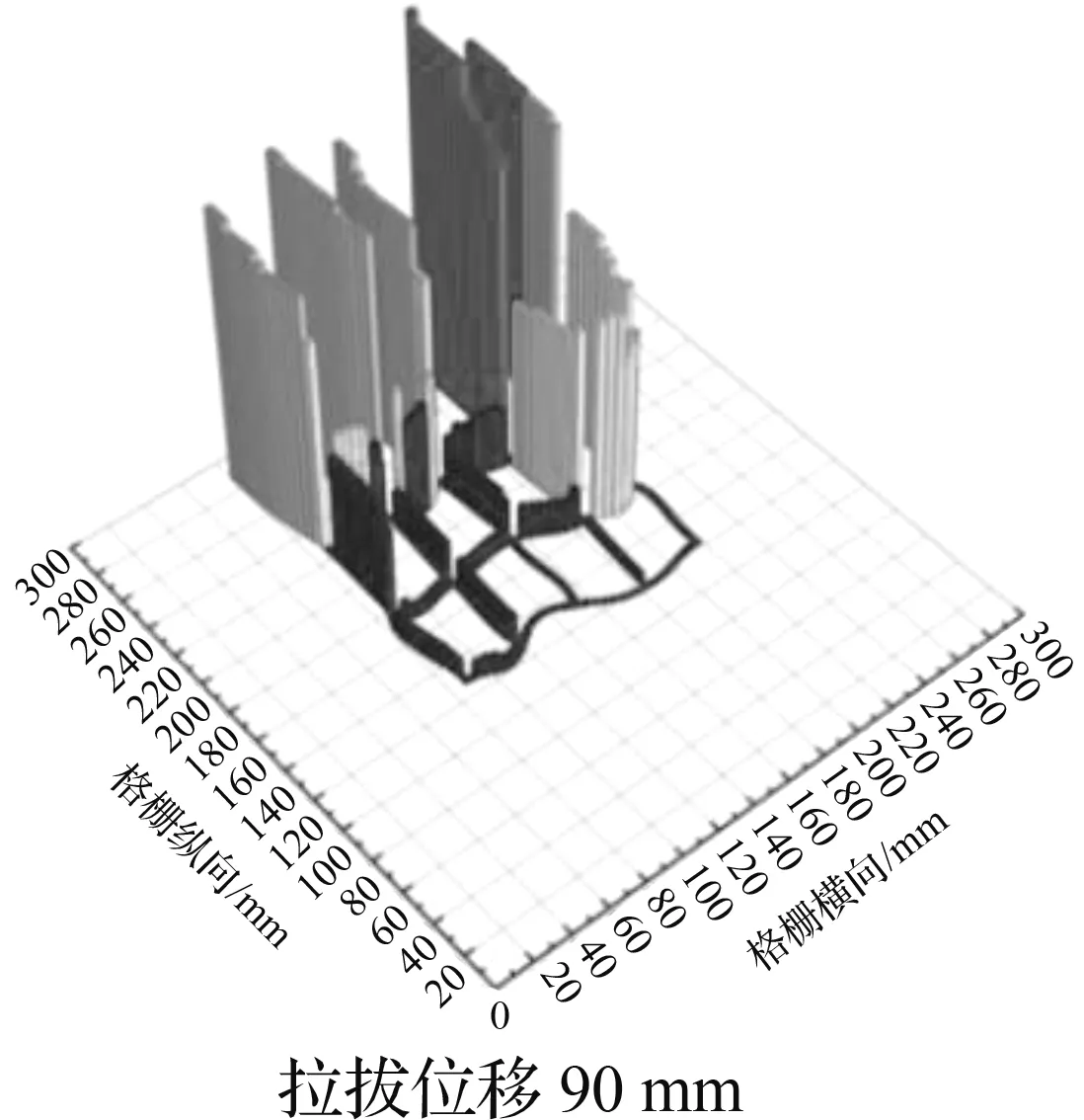
根据本文前述各工况下拉拔力随拉拔位移发展情况分析，遴选出具有代表性的较优工况并给出其在50 kPa法向压力下拉拔位移63 mm(峰值拉拔力左右)及拉拔结束时格栅轴力分布柱形图，如图5所示。各阶段下纵肋轴力变化与整体拉拔力的波动相互对应，同时，各阶段下首条横肋的轴力均高于其他横肋。

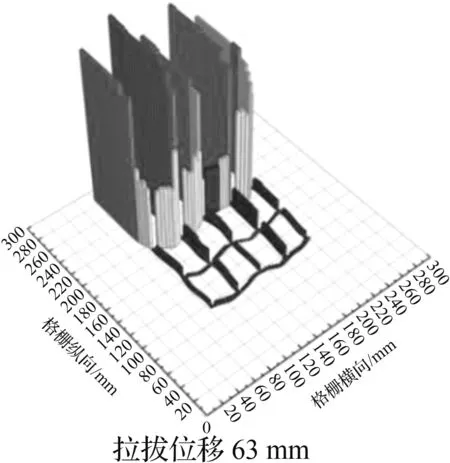
(a) 工况2

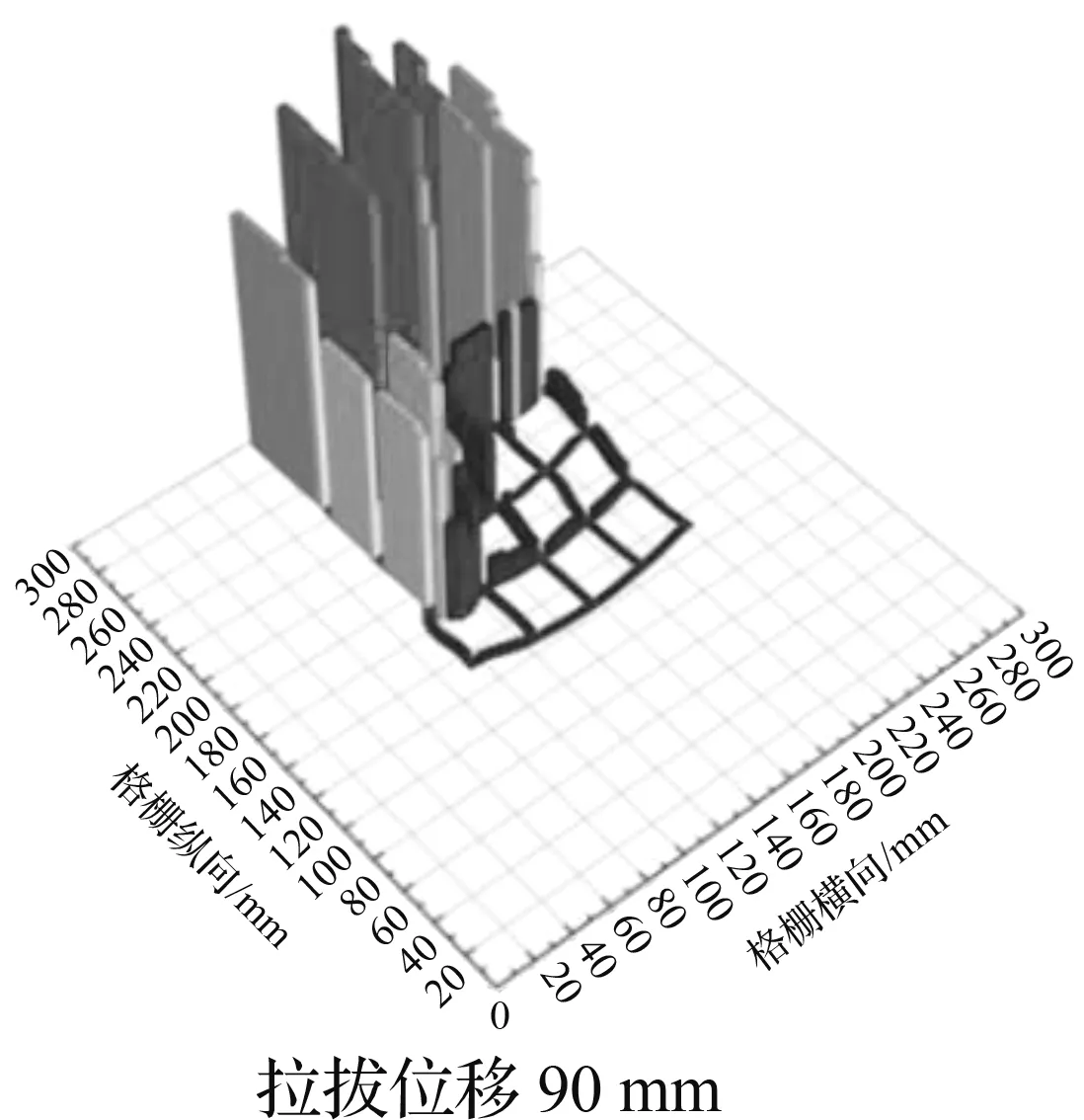
(b) 工况3

(c) 工况6

对比拉拔位移63 mm时各工况的筋材轴力，可以看出工况3中筋材轴力分布更加均匀，且其肋条横向变形较小，网孔几何形状保持得更好。内部网孔结构的轴力发展充分说明了随着拉拔进程的深入内部格栅逐渐被调动从而有效提高了筋材整体的抗力，而格栅与道砟之间相互作用的增强，使其拉拔阻力得到进一步提升。这也从应力分布角度解释了工况3的峰值拉拔力较其他工况高的原因。工况2在拉拔结束时与拉拔63 mm对比，末端横肋呈现明显的收缩变形，且末段肋条的轴力也相对变小。从细观角度分析，格栅末端约束条件的变化及道砟颗粒的存在显著改变了接触点处应力的峰值及分布形式。

拉拔过程中肋条的移动和变形将会引起内力重分配，进而引起筋土强相互作用区域的改变。纵观各工况下肋条变形规律，拉拔终态时格栅轴力分布区域的横肋表现出横向收缩，而纵肋则轴向伸长，填料深处格栅轴力分配也较峰值时表现出不均匀性。同时，各工况呈现出的筋材肋条整体变形情况也与前述拉拔力发展规律的分析一致。

3 网孔尺寸对筋土界面特性的影响

3.1 格栅横肋对加筋性能的影响

如图6所示，在无横肋的情况下可以认为格栅纵肋与级配道砟间的摩阻力为拉拔阻力的唯一来源，所以工况8各级法向应力下拉拔力的峰值和其对应的位移均远小于其他工况。与图5对比可见横肋承载阻力在拉拔阻力构成中起着重要作用，这与杨广庆等[16]开展的室内单向土工格栅(剪切面上无横肋)直剪摩擦试验的结果基本一致，也说明土工格栅横肋与道砟颗粒之间的端承力对筋土界面的摩擦特性具有重要贡献。

图6 工况8拉拔力-拉拔位移关系曲线Fig.6 Variation of pullout force curve of scheme 8

图7 工况7格栅轴力分布柱形图Fig.7 Geogrid axial force distribution of scheme 7

图7为去掉末条横肋的格栅(工况7)在50 kPa法向压力下拉拔位移63 mm的轴力分布图，在缺少横肋的情况下其末端纵肋轴力在节点后急剧下降，可见横肋是格栅受力的关键部位之一。对比图6，发现由于横肋的缺失导致末端纵肋缺少横向约束，在级配道砟的挤压和摩擦下横向位移表现出一定的随机性。进一步说明完整横肋能使得筋土界面的加筋作用得到充分的发挥，并且随着横肋数不断地减少，这一特征更加明显。所以在工程应用中需特别注意避免横肋的施工损伤，以免影响整体的加筋效果。

3.2 网孔尺寸影响格栅加筋性能的细观分析

本文以工程中广泛应用的筋土界面强度指标-拉拔摩擦系数f为标准从细观角度评价格栅网孔尺寸对加筋性能的影响。与宏观力学类似，细观力学中两接触实体间滑动行为由两者间较小的摩擦系数及接触力法向分量共同决定，除了与筋材肋条直接接触的颗粒之外，拉拔过程中格栅通过表面摩擦性能带动周围颗粒运动。因拉拔过程中始终保持匀速拉拔，假定格栅上下界面处剪应力分布均匀且与拉拔力满足静力平衡关系，则拉拔摩擦强度可由式(1)求得在摩尔-库仑强度准则下，对峰值拉拔力导出的拉拔摩擦强度(剪切强度)与该工况下各级法向应力进行线性拟合即可由式(2)得到筋-土界面强度指标，图8为各工况下拉拔摩擦强度-法向应力的线性拟合结果。

(1)

(2)

式中:τ为峰值拉拔力下的拉拔摩擦强度；F为各级法向应力下的峰值拉拔力；L,B分别为填料内部格栅的长度和宽度；f为拉拔摩擦系数；P为法向压力。

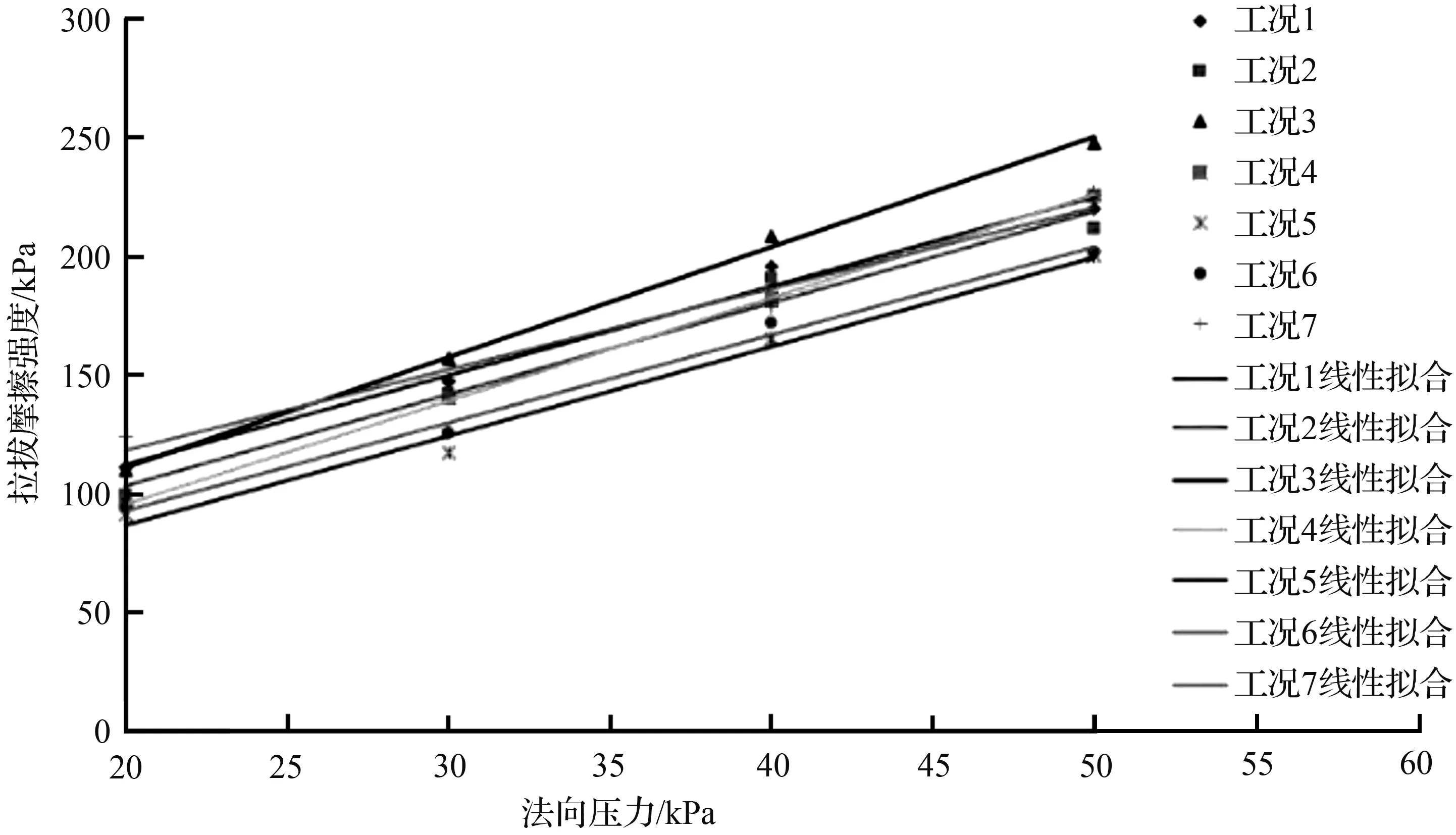
图8 筋土界面强度线性拟合Fig.8 Linear fitting of strength index of reinforced geogrid-ballast interface

值得说明的是，由前述对工况8的分析可知，在纵肋数目相同的情况下无横肋的格栅整体承载阻力峰值与完整网孔结构的格栅阻力峰值比值为8.32 %～10.91 %，为了避免首条横肋之前的纵肋对筋土界面强度指标的影响，本文对式(1)中L、B的取值调整为填料内部格栅总网孔的长度和宽度，以格栅有效网孔面积进行拉拔摩擦强度的计算。

表2为拟合得到的各工况下筋土界面强度指标及拟合优度，由表2中拉拔摩擦系数和拟合优度可以看出相较于其他工况，工况3网孔尺寸的格栅对本文级配道砟的加筋效果最为出色。综合分析可知，网孔尺寸对于格栅加筋性能的发挥起着决定性作用，在工程中应结合筋材-填料的受力方式科学合理的选择双向土工格栅的网孔尺寸。

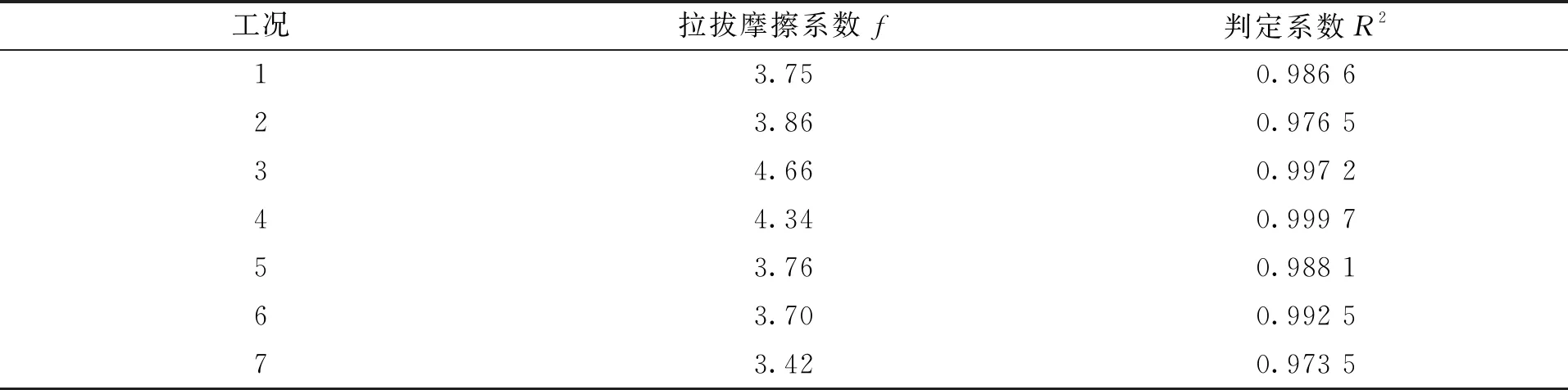
表2 筋土界面强度指标及拟合优度Tab.2 Strength index and goodness of fit of geogril-ballast interface

4 结论

本文在考虑道砟级配的情况下，基于拉拔阻力变化、筋材轴力分布及格栅肋条变形情况对不同网孔尺寸下双向土工格栅加筋道砟的筋土界面细观特性进行对比分析，主要结论总结如下：

① 格栅纵肋尺寸对拉拔进程中横肋调动有一定的影响，而横肋尺寸则有效影响纵肋的横向位移;

② 通过对缺少格栅横肋工况的对比分析，揭示了双向土工格栅的横肋承载阻力在拉拔阻力构成中的重要作用，土工格栅网孔结构的完整使得筋土界面的加筋作用得到充分的发挥;

③ 合理的网孔尺寸下格栅可以在主动拉拔下较好地保持原有的几何形态从而提高其与道砟颗粒之间联合作用的被动阻抗;

④ 以筋土界面强度指标为评价标准，在本文道砟级配结构下工况3网孔尺寸的双向格栅综合加筋性能最优。