网孔电流方程的改进和广义网孔电流方程的建立

彭爱莲

(商丘师范学院 电子电气工程学院，河南 商丘 476000)

在分析复杂的线性时不变的平面电路时，网孔电流法是一种普适的方法，尤其对于支路数较多而网孔较少的电路，运用网孔法求解电路最方便和快捷.网孔电流法是以网孔电流为变量，依据基尔霍夫电压定律(Kirchhoff′s voltage law，KVL)列出每个网孔的电流方程，通过方程组求得各网孔电流，进而得到电路中每条支路的电压、电流和功率[1].

在含有多个无伴电流源的电路中，为了避免引入网孔电流以外的变量，通常把含有公共电流源支路的、相毗邻的网孔所构成的回路看作一个广义网孔，广义网孔的电流方程目前没有统一的公式[2-4].本文中，在对网孔分类的基础上，对普通的网孔电流方程进行改进，并对广义网孔的KVL方程进行分析，总结出广义网孔电流方程的一般表达式.本文中，网孔的绕行方向和网孔电流的方向均取顺时针方向，用imk表示第k个网孔的电流.

1 普通网孔电流方程的改进

具有m个网孔的平面电路，网孔k的电流方程的一般形式为[1]：

Rk1im1+Rk2im2++Rkkimk+Rkmimm=uskk

(1)

如果对电路中的网孔进行分类，依据与网孔k的关系，可分成三类，第一类是不与k毗邻的网孔；第二类是与k毗邻的网孔；第三类是k自身.第一类网孔与k之间的互电组均为0，因此，公式(1)中相应的项可以去除.如果将第二类网孔记为i，公式(1)可以改写为：

(2)

公式(2)表明，在列写网孔k的电流方程时，主要是观察电路中与k毗邻的网孔和k自身，计算出互电阻和自电阻.电路中不与k毗邻的网孔，其网孔电流和相应的互电阻可以不列在方程的表达式中，公式(2)是对公式(1)的精简，是普通网孔电流方程的改进.

用图1示例比较公式(1)，(2)的不同.图1中，从左向右共4个网孔，依次记为网孔1，2，3和4，其网孔电流依次为im1，im2，im3和im4.以网孔1和2为例，应用公式(1)，电流方程分别为：

R11im1+R12im2+R13im3+R14im4=us11

(3)

R21im1+R22im2+R23im3+R24im4=us22

(4)

利用改进后的方程(2)，网孔1和2的电流方程可写为：

R12im2+R11im1=us11

(5)

R21im1+R23im3+R22im2=us22

(6)

公式(3)和(4)中，共需要计算10项，而公式(5)和(6)中，共需要计算7项.因此，利用改进后的公式，计算量有效降低，对于含有更多网孔的电路中，计算量的降低会更加明显.

图1 比较公式(1)和(2)的电路图

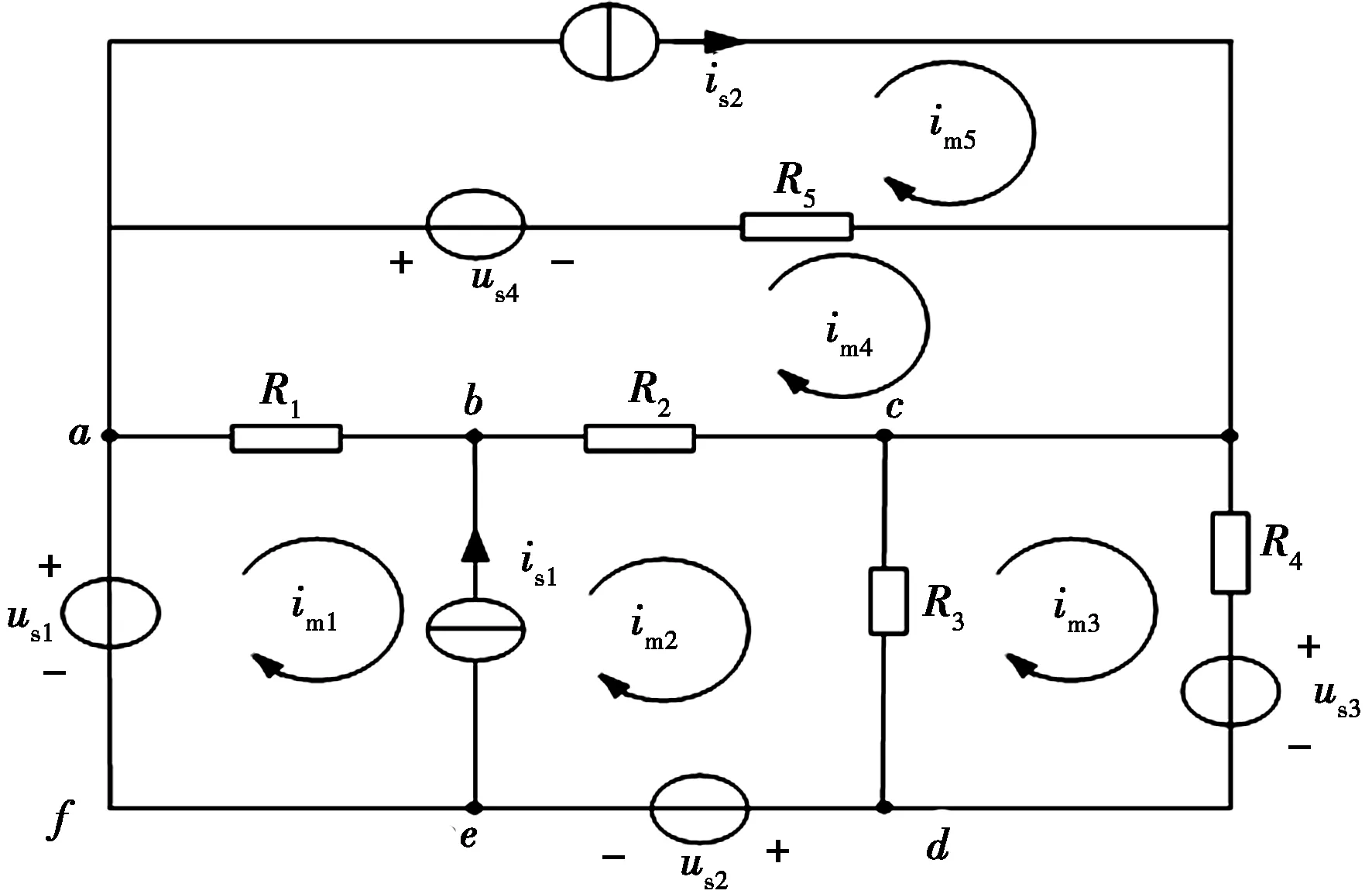
图2 具有公共无伴电流源支路的电路

2 广义网孔电流方程的建立

在含有多个无伴电流源的电路中，若某无伴电流源所在的支路是两个网孔的公共支路，如图2中的is1.

依据公式(1)或公式(2)列写网孔1和2列电流方程时，都必须引入电流源is1的两端电压作为电路变量，方程的难度增大.如果将回路abcdefa作为一个广义网孔，记为网孔A.A的KVL方程为R1(im1-im4)+R2(im2-im4)+R3(im2-im3)+us2-us1=0，整理可得：

-R3im3-(R1+R2)im4+R1im1+(R2+R3)im2=us1-us2

(7)

观察图2可知，公式(7)中的网孔电流分为两类，一类是与A毗邻网孔的电流，即im3和im4，其系数分别是A与网孔3、4公共支路上的电组的负值，因此可令：RA3=-R3，RA4=-(R1+R2)，分别称为A与网孔3、4的互电阻.另一类是A内部网孔的电流，即im1和im2，其系数分别是各自网孔上的电阻之和，因此可令：R11=R1，R22=R2+R3，分别称为网孔1、2的自电阻.等号右边是A边沿支路上的电源电压的代数和，令：usAA=uS1-uS2，公式(7)可写为：

RA3im3+RA4im4+R11im1+R22im2=usAA

(8)

依据各网孔与A的关系，公式(8)可看作由三部分组成，第一部分是与A毗邻网孔的电流项，即RA3im3+RA4im4；第二部分是A内部网孔的电流项，即R11im1+R22im2；第三部分是usAA.依据此结构特点，可以将公式进行推广，若电路中与A毗邻的网孔记为i，A内部的网孔记为j，则广义网孔A电流方程的一般表达可书写如下：

(9)

公式(9)表明，在列写A的电流方程时，主要是观察电路中与A毗邻的网孔和A自身，计算出互电阻RAi和自电阻Rjj.电路中不与A毗邻的网孔，如图2中的网孔5，与A的互电阻为零，其网孔电流im5不列在方程的表达式中，该特征与改进的普通网孔电流方程的特征相同[5].

特殊情况下，若A中的网孔只有一个，则广义网孔变成一个普通的网孔.若设A只包含一个网孔k，则网孔j也等于网孔k，则有如下公式：

(10)

公式(10)和公式(2)表达形式完全相同，即公式(9)不仅适用于以无伴电流源为公共支路的广义网孔，也适用于普通网孔.

3 广义网孔电流方程的推广应用

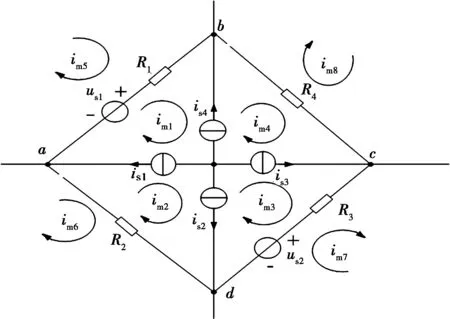
图3 含有多个相连的无伴电流源的电路

当电路中存在多个相连的无伴电流源时，可把以这些电流源为公共支路的所有网孔所构成的回路看作一个广义网孔.如图3所示，把回路abcda作为一个广义网孔，记为网孔B.对B列KVL方程：R1(im1-im5)+R4(im4-im8)+R3(im3-im7)+R2(im2-im6)+us2-us1=0，整理可得：

-R1im5-R2im6-R3im7-R4im8+R1im1+R2im2+R3im3+R4im4=us1-us2

(11)

观察图3可知，公式(11)的组成也是分为三部分，公式的前4项属于与B毗邻的网孔电流项；公式的第5、6、7、8项属于B内部的网孔电流项；等号右边是B边沿支路上的电源电压的代数和.若与B毗邻的网孔记为i，B内部的网孔记为j，则公式(11)可分写为：

其中RBi是B与网孔i的互电阻，Rjj是网孔j的自电阻，usBB是B边沿支路上的电源电压的代数和，则公式(11)可重新写为：

(12)

公式(12)与公式(9)在形式上是完全一致的，以此推断，公式(9)也适用于以多个相连的无伴电流源为公共支路的广义网孔[6-8].

4 结 论

电路中不与网孔k毗邻的网孔，与k之间的互电阻均为0，普通网孔电流方程中相应的项可以去除，方程的表达式得到精简.以无伴电流源为公共支路的、相毗邻的网孔所构成的广义网孔，其KVL方程可以划分为三个组成部分，第一部分是与广义网孔毗邻的网孔电流项；第二部分是广义网孔内部的网孔电流项；第三部分是广义网孔边沿支路上的电源电压的代数和.依据此结构特点，总结出广义网孔电流方程的一般表达式.分析证明，公式(9)不仅适用于以单个或多个相连的无伴电流源为公共支路的广义网孔，也同样适用于普通的单个网孔，属于更广泛意义上的网孔电流方程.