用超网孔分析法列、解含无伴电流源电路方程

张汉飞,刘祖云

(1.仙桃职业学院，湖北仙桃433000;2.湖北省楚天网络广播责任有限公司，湖北仙桃433000)

用超网孔分析法列、解含无伴电流源电路方程

张汉飞1,刘祖云2

(1.仙桃职业学院，湖北仙桃433000;2.湖北省楚天网络广播责任有限公司，湖北仙桃433000)

以探讨电路网孔的画法为切入点，对电路的网孔进行了扩展定义，提出超网孔的概念。运用超网孔分析无伴电流源电路简单易行，可用观察法直接列出电路方程，而无需列约束方程或重新绘制电路图等，使电路方程数量减少，求解方便。同时，总结出了解题步骤，便于指导学习。通过例题的解析，证明该方法简单、可行。

超网孔；无伴电流源；电路分析

0 引言

在电路分析中，网孔电流法因其列方程简单、列出的行列式具有对称性而深受学生喜爱。但是当两网孔中间出现一个或多个无伴恒流源时，需列约束方程，增加解题难度；回路电流法对回路的选择具有灵活性，可以列出任何电路的KVL方程，但列出的电路方程组一般不具备对称性，出错后不方便查找错误，因此不受学生欢迎。所以，针对这两种电路分析方法的优缺点，本文提出了应用超网孔分析法列、解含无伴电流源电路。

1 超网孔分析法的理论分析

通过以前的学习我们知道，一条支路只作为一个网孔边界的情况称为“单相关”，和网孔单相关的支路显然都是电路最外沿的支路，每一单相关支路中流过的是与它关联的网孔电流。这就意味着，如果一个理想电流源支路是单相关支路，则它所在网孔的电流便是已知的，于是该网孔的方程就不需列写，这样便减少了方程的数目。这种方法称为“电流源支路单相关”法。如果理想电流源支路在电路中是两个网孔的公共支路，则往往能通过用改画电路图的方法将双相关的恒流源改画成单相关恒流源。

例如，图1(a)所示电路，由于无伴电流源Is在网孔Im1和Im2的中间，是两个网孔的公共支路，我们可以将电路图进行重新绘制。画成图1(b)的形式，本来是双相关的恒流源Is在图1(b)中变成了单相关恒流源，根据图1(b)所设定的网孔电流用观察法可列出网孔方程如下：

(R2+R3+R5)Im1－R5Im2－R2Im3=0

－R5Im1+(R1+R5+R4)Im2－R1Im3=US1

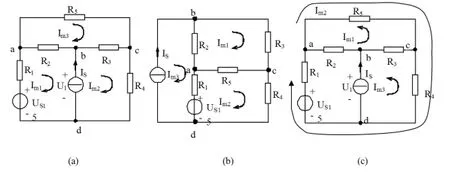
图1

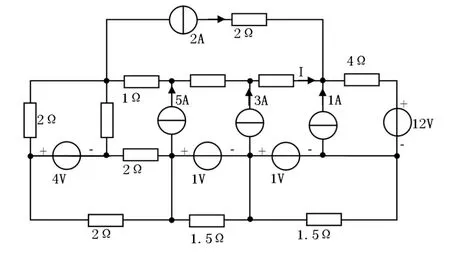
图2

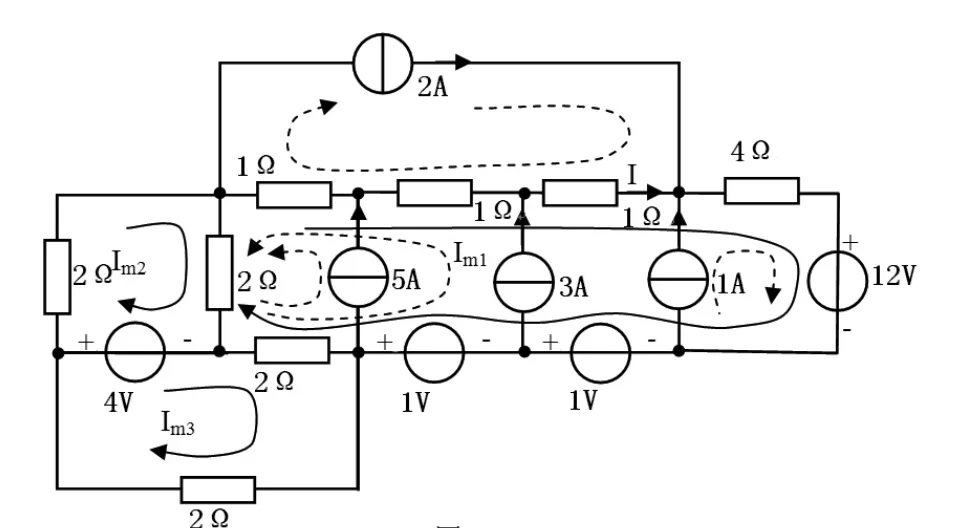
图3

Im3=Is

解以上二元一次方程即可解出Im1和Im2。

将图1(b)中的网孔电流重新画到图1(a)上就可以得到图1(c)，通过图1(c)我们可以看到：

(1)图1(a)的外沿原本是一个网孔，要使用该网孔列方程时其绕行方向必须与内部网孔绕行方向相反；同理包含多个已知无伴恒流源的网孔原本也是一个网孔；与这相反单网孔也可以变成超级网孔。

(2)将已知的无伴恒流源仅使用一次而将与之相关的网孔空出即可认为该无伴恒流源为单相关恒流源；

(3)各支路电流是该支路的两相邻网孔电流的代数和。与没设置网孔电流相邻的网孔为单相关网孔，其支路电流为相关的网孔电流。

2 应用超网孔分析法列、解含无伴电流源电路的基本步骤

通过上面的实例分析，可以将超网孔分析法列、解含无伴电流源电路的基本步骤归纳如下：

（1）将待求电路化分为几个排列有序的未知电流网孔，该未知电流网孔可包含若干已知恒流源网孔；

（2）将已知的恒流源网孔分别单独列出；

（3）用观察法按网孔电流方程规则列写网孔方程；

（4）求解网孔方程；

（5）根据已解出的网孔电流求解各支路电流。

例3、求解如图4所示电路电流I

解：第一步，将电路化简，与恒流源串联的电阻可视为短路，与恒压源并联的电阻可视为开路。化简后的电路图如图5所示，该图有7个网孔，有4个已知无伴恒流源，因此只要列3个未知网孔电流就行了，3个未知网孔电流用实线箭头表示，已知的网孔电流用虚线箭头表示，可用观察法列出方程如下：

(2+2+1+1+1+4)Im1－2Im2－2Im3－(1+1+1)×2－(1+2+2)×5－(1+1+2+2)×3+4×1=－12+1+1

－2Im1+4 Im2+10+6=4

－2 Im1+4Im3+10+6=－4

整理后得：

11Im1－2Im2－2Im3=35

－2Im1+4Im2=－12

－2 Im1+4Im3=－20

解此方程组得：

Im1=2.111A

Im2=－1.944A

Im3=－3.944AI=Im1－2=0.111A

3 结论

应用超网孔分析法列、解含无伴电流源电路，结合了无伴电流源电路的特点，很方便地列出电路方程，并且和传统的电路分析方法相比，大大减少了列方程的数量，是一种分析无伴电流源电路的新方法。

[1]Paul Horowitz.电子学 [M].北京，电子工业出版社，2011.

[2]徐国洪.电工技术与实践[M].湖北，湖北科学技术出版社，2008.

[3]邱关源.电路[M].北京，高等教育出版社，2006.

（编辑 赵欣宇）

On Listing and Solving Solitary Current Source Circuit Equations by Ultra Mesh Analysis Method

ZHANGHanfei，LIUZuyun
（1.XiantaoVocational College，Xiantao433000,China;2.Hubei Chutian Network Broadcast LLC，Xiantao433000,China)

With the discussion ofthe drawingofthe circuit mesh as the breakthrough point,the mesh ofthe circuit experiences extended definition.Put forward the concept of ultra mesh.Using the ultra mesh to analyze solitary current source circuit is simple.Using the method of observation can list circuit equations directly,without constraint equations or redrawing circuit diagrams,etc.to decrease the number of circuit equations and to solve equations conveniently.At the same time,summarize the solving steps,which is convenient for guiding learning.Through the analysis of examples,it proves that the method is simple and feasible.

ultra mesh;solitarycurrent source;circuit analysis

TM133

B

1672-0601（2015）10-0062-02

2015-09-10

张汉飞（1981-），男，学士学位，讲师，主要研究方向：电子信息技术。