基于磨损量正态分布刀具可靠性模型及验证
崔昌,石伟伟,胡珊珊*,覃梦玲
(广西大学 机械工程学院,广西 南宁 530004; 广西科技信息网络中心,广西 南宁 530022)
0 引言
碳化硅陶瓷以其优异的抗热震、耐高温、抗氧化和耐化学腐蚀等特性而广泛地应用于石油化工、汽车、机械和航空航天等工业领域中[1]。然而碳化硅陶瓷作为非金属难加工材料,在加工过程中刀具的磨损剧烈,且易产生崩刀、断刀等现象,因此加工时及时了解刀具的可靠度尤为重要[2-4]。在金属加工领域中,国内外学者对多种加工条件下刀具的可靠性及可靠性模型理论开展了大量研究,通过采集刀具信号特征并提取后,运用了随机响应面法和蒙特卡罗抽样等方法建立了可靠性估计模型,并对刀具的工作状态分析和寿命预测[5-6];文献[7-9]基于可靠度函数计算并得到了更换刀具的最佳时间,并成功预测了刀具的磨损状态。
而在非金属材料加工领域,在宏观和介观尺度,非金属材料的去除过程以脆性断裂为主,其加工刀具的耐用度和可靠性与金属加工刀具相去甚远,而国内外针对非金属材料加工的刀具的研究主要集中在探索刀具适用性及预测刀具磨损状态等方面[10-12],并不能准确估计持续加工过程中刀具的可靠性。因此,为了研究加工非金属脆硬材料刀具的可靠性,选用高温烧结制成的金刚石刀具,并选择非金属脆硬材料碳化硅陶瓷作为工件,通过采集刀具一定时间内的持续磨损量作为刀具性能退化数据,并结合统计学中贝叶斯相关理论,建立了基于退化量正态分布的可靠性模型,来研究非金属脆硬材料在加工过程中刀具的可靠性问题。
1 可靠性建模方法
关于产品性能退化数据建模的方法很多,但由于碳化硅陶瓷孔加工试验时间长、成本高,获得的数据样本小,因此本文通过采集刀具的持续磨损量,采用基于退化量分布的建模方法评估刀具的可靠性。具体建模流程见图1。
1.1 确定分布模型
首先要确定刀具退化数据的分布模型,将采集到的刀具磨损量数据导入SPSS软件,利用软件中的P-P图对数据进行分析,然后对数据进行Weibull分布、正态分布、指数分布、伽马分布和对数正态分布等拟合,同时将各种分布拟合后的结果进行对比,最后选取一种最适合描述刀具退化数据的分布模型,接着进行拟合优度检验,根据数据的类型和特点选用的是非参数检验中的K-S检验。
1.2 确定先验分布
设x1,x2,…xn为实验的原始数据,且x1≤x2≤…≤xn为截尾数据。假设通过拟合确定最适合描述刀具退化数据的模型是正态分布,则可以确定先验分布如下:
正态分布概率密度函数为
(1)
可靠度函数为
(2)
式中:x>0;σ>0,为标准差;μ∈R,为均值。
通过使用最小二乘估计法对采集到的刀具退化数据回归分析,可以得到正态分布中的参数μ、σ,并将参数μ、σ作为已知的样本。为了扩大样本的数据,再对区间(0,1)上随机数组e[n]抽样,这里使用的是蒙特卡罗抽样法,同时再反求出正态分布中的随机变量,其中通过抽样得到的样本总数记为M组。
由蒙特卡罗抽样公式有
(3)
抽样结束后,需要对抽样的数据x[n]先进行排序,并将得到的数据依次同采集到的实验截尾数据对比,在比较中若第l个数据,有x[l]>D,则x[l]=D,通过这种方法可以得到相应的抽样数据,所得到的抽样数据用最小二乘估计法进行参数估计,这样得到每组数据对应的μi、σj,并将每组数据的参数估计值分别保存在其对应的数组μ[i]、σ[j],此时保存到每一个数组的值相互独立,由此便可以得到μ和σ的联合概率密度为
(4)
由贝叶斯统计相关理论可以得到μ、σ的联合概率密度均为常数。
(5)
其中:i=1,2,…,M;j=1,2,…,M。上式(5)即为确定的先验分布公式。
1.3 贝叶斯公式计算
在统计学中,贝叶斯公式是计算概率的重要公式,其表达式为
(6)
在上式中,若刀具磨损量数据服从正态分布,则θ为正态分布中的μ、σ;g(θ)为θ的先验概率密度,g(θ|x)为对应的后验信息;x为样本X的观测值;f(x)为关于x的函数;在给定θ时f(x|θ)可以看做X条件分布密度,可以近似地看作似然函数,即f(x|θ)=L(x|θ)。
当参数样本值已知的情况下,正态分布的概率密度函数可以看做条件分布。
(7)
似然函数为
(8)
其中:r为样本个数。
由式(5)已知贝叶斯先验分布,并根据贝叶斯公式结合蒙特卡罗抽样和先验信息即可以得到
(9)
式中:i,j=1,2,…,M。式(9)为关于μ、θ的贝叶斯后验概率密度公式[13]。
1.4 可靠度计算
在给定样本的情况下,可靠度R可以看做一种函数,即R=f(m,η),结合概率统计中分布函数相关知识,由此可以确定关于R的后验累计分布函数为
(10)
式中:m为形状参数,η为尺度参数。
通过对公式(10)求导便可以得到分布函数对应的概率密度函数为
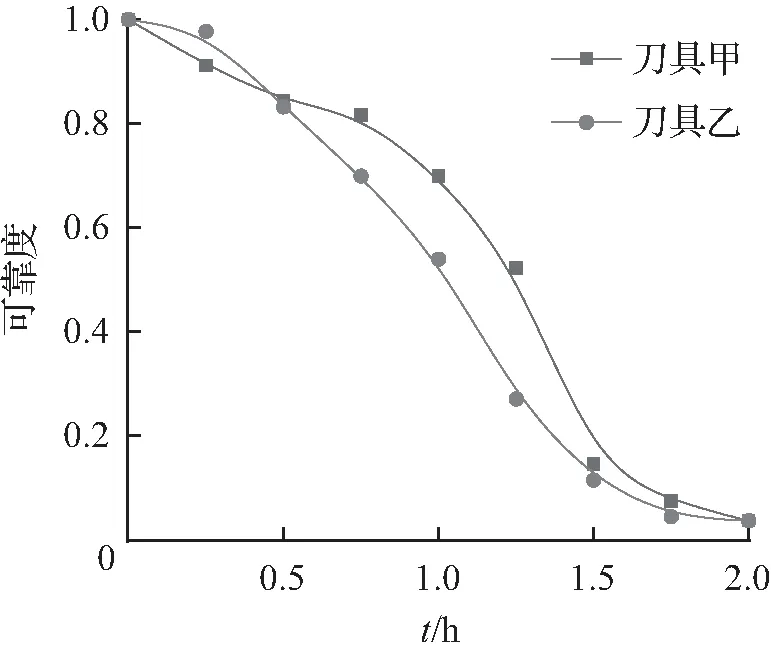
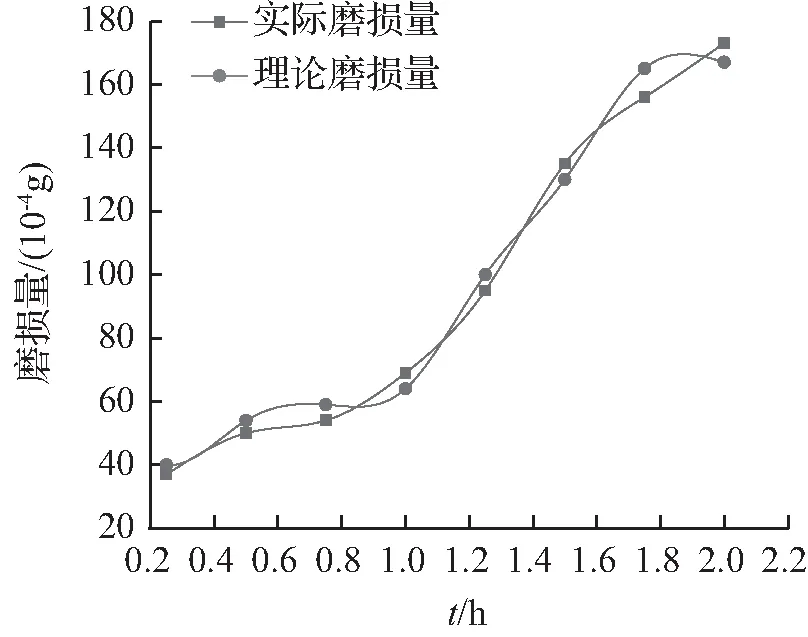
fR(r)=FR′(r),0 (11) 然后,对概率密度函数积分可以得到可靠度每个点的估计值为 (12) 上述计算可靠度R值的方法显然较为繁琐,在实际加工过程中,为了更快速地计算可靠度的值,可以采用数值分析方法来求解。根据上述公式推导过程和式(9),可以求出可靠度函数的点估计值为 (13) 由式(13)可求出刀具在每一次固定测量时刻的可靠度Rj,表示为(tj,Rj),j=1,2,…,n,若在实验过程中刀具性能退化数据服从正态分布,可以计算出刀具在某一确定时刻的可靠度,同时利用计算出的可靠度值对未知的参数估计,最后求出刀具的失效模型。 在钻削实验中,刀具磨损的影响因素有很多,但主要取决于机床主轴的转速、刀具切削深度、进给速度,而实验中采集到的最终数据是刀具在一定加工时间内的磨损量,因此实验设计每次钻削相同的深度。结合实验设备和实际加工情况,经过预实验反复探索最终得到适合本实验的最佳参数,主轴转速n为7 000~10 000 r/min、进给速度Vf为0.2~0.5 mm/min。实验采用3把刀具,分别记为刀具甲,刀具乙,刀具丙;采用直孔钻削的加工方式;同时采用纯油性切削液以浇注的方式冷却,流速120 mL/min。采用单因素实验法进行加工实验,所选因素水平见表1。 表1 实验各因素对应水平Tab.1 Corresponding levels of each factor in the experiment 刀具磨损量的测量方法有很多,但是由于本实验所用的金刚石刀具的特殊性,刀具的磨损主要集中在工作层圆柱面和刀具唇面,考虑到实验所使用的刀具和工件材料均属于脆硬材料,在实验过程中不会出现黏刀等情况,结合众多学者研究[14-16],最终选择钻削前后刀具的质量变化△M来评估刀具的磨损程度。 实验时所用的设备为日本FANUC的ROBODRILL_@-T14iFlb型数控机床,最高转速为24 000 r/min;采用上海力辰科技有限公司生产的FA324TC高精度电子分析天平测量刀具磨损前后的质量变化,测量精度为0.1 mg,最大称量质量320 mg。实验采用河南中拓磨料磨具有限公司生产的烧结金刚石钻头,该钻头既有金刚石强度高、耐磨性强等优点,又具有硬质合金抗冲击性强度高、出刃大等特点,其基体材料为高速钢,钻头外径为5 mm,内径2 mm。工件材料选用浙江鑫飞达电子有限公司生产的无压烧结碳化硅陶瓷,这种陶瓷以高纯度、超精细的碳化硅粉为原料并加入适量的烧结助剂高温烧结制成,所得制品致密性良好。 在实验过程中,切削力和振动等动态信号从侧面描述了加工状况,但是刀具在固定测量时间前后的质量变化ΔM更适合作为刀具性能退化数据,左转速为8 500 r/min,进给速度为0.5 mm/min工况下刀具持续磨损量的测量值见表2。 表2 刀具持续磨损量测量结果Tab.2 Measurement of toolwear duration 以表2中刀具的磨损量为分析指标,结合第1章提出的方法对刀具进行可靠性分析,结合实际加工状况以及与厂家沟通,将刀具失效阈值设为150×10-4g。首先借助SPSS软件对刀具甲、刀具乙、刀具丙的磨损量按照1.1所述方法分布拟合,拟合后各分布的拟合偏差值见表3。 表3 拟合偏差值Tab.3 Fitting deviation value 本文的显著性水平为α=0.05,通过表3可以看出:拟合后5种分布中正态分布的偏差值最小,这说明正态分布更适合描述金刚石刀具钻削碳化硅陶瓷的磨损量。接着根据K-S检验理论对拟合后的分布进行检验,SPSS软件结果显示渐进显著性(双侧检验)的P值为0.200,大于给定的显著性水平,进一步说明描述刀具磨损量最合适的分布为正态分布。 由上述对刀具磨损量数据拟合的对比,已经确定刀具磨损量△M最合适的分布为正态分布,正态分布概率密度函数为 (14) 累计分布函数为 (15) 上式可以转换为 (16) 则将式(15)转化为线性回归方程: y=a+bx。 (17) 为了求出t值,首先需要估计对F(w),这里可以利用中位数的方法来估计对F(w)的值,表达式为 (18) 其中:i为在测量过程中刀具磨损量的顺序,n为总的样本数。然后利用线性回归的方法对正态分布中的参数μ、σ进行估计。 由式(17)可以估计出F(w)的值,利用最小二乘法结合测量的刀具磨损量计算出a和b的值,用MATLAB软件编程计算出参数μ、σ的值,结果见表4。 表4 参数估计值Tab.4 Parameter estimates 以表4中刀具甲的参数估计值μ=95.247、σ=55.514为例,按照前文所述方法抽样得到满足刀具性能退化的数据,对不同的抽样结果进行比较,发现抽样在30次左右结果相对较为稳定。并利用最小二乘法对每组抽样数据进行参数估计,得到正态分布的参数μi、σj。 表5 抽样样本的参数估计值Tab.5 Parameter estimates of the samples 结合表5的参数估计值和贝叶斯公式求出参数μ、σ的概率分布,代入式(12)得到刀具甲在每个测量时刻的可靠度,同时根据以上方法计算出刀具乙的可靠度值,将2把刀具的可靠度值进行拟合,最终得到2把刀具可靠度的变化趋势见图2。 图2 刀具甲、乙可靠度随时间的变化趋势Fig.2 Reliability of tool A and B over time 为了更直观地验证模型的准确性,根据测量时刻刀具甲、刀具乙的可靠度值,联合式(2)、(3)、(11)、(12)、(18)计算出二者的理论磨损量,结合上文中测得的实际磨损量,绘制出2把刀具的实际磨损量与理论磨损量对比曲线见图3至图4。 图3 刀具甲实际磨损量与理论磨损量对比Fig.3 Comparison of actual and theoretical wear of tool A 图4 刀具乙实际磨损量与理论磨损量对比Fig.4 Comparison of actual and theoretical wear of tool B 由图3至图4可以明显看出:经过计算,2把刀具实际磨损量与根据可靠度模型计算出的理论磨损量拟合的结果基本一致,最小误差为1.3 %,最大误差为7.6 %,证明了建立的可靠度分析模型具有较高的准确性,结果表明通过这种方法可以准确地估计刀具在每个时刻的可靠度,所得到的可靠度能够反映刀具钻削过程中实际的工作状态,为加工过程中是否需要换刀提供理论参考。 从碳化硅陶瓷加工过程中刀具的可靠度问题出发,以最直观的刀具磨损量作为描述刀具退化的指标,从退化量的角度对刀具的可靠性进行评估,并结合贝叶斯理论提出了刀具可靠性分析方法,从数学理论的角度建立了一种磨损量数据服从正态分布的可靠度分析模型,对模型中的参数采用最小二乘法进行估计计算,首先将实验中转速为8 500 r/min,进给速度5 mm/min下的2把刀具的磨损量ΔM进行拟合分析并选择合适的分布模型,后用贝叶斯理论确定先验分布,最终确定了刀具的可靠度模型,经过计算得出了刀具在每个时刻的可靠度,并通过最后刀具实际的磨损量与根据可靠度模型计算出的磨损量对比,发现两者误差较小,从而验证了模型的可行性。结果表明这种方法可以准确地估计刀具在每个时刻的可靠度,为更快速、准确确定非金属加工过程中刀具的可靠性提供了一种有效途径。2 实验方案及设备
2.1 实验方案

2.2 实验设备及材料
3 实验结果与刀具可靠性分析
3.1 实验结果

3.2 确定分布模型

3.3 可靠性分析
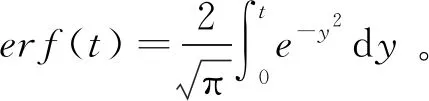



4 结论

