公路桥梁组合跨度结构锚固区应力集中系数研究









作者简介:黄萍萍(1987—),工程师,研究方向:公路工程技术。
摘要:为研究公路橋梁组合跨度结构锚固区的应力-应变状态,文章采用LIRA程序建立有限元模型,对公路桥梁组合跨度结构锚固区的应力集中系数进行数值研究,并分析了法向应力沿跨度结构高度和长度分布的性质。所获得的系数可用于现有桥梁设计的耐久性和强度计算,也可用于确定桥梁结构的剩余寿命以及预测其使用寿命。
关键词:组合结构;应力集中系数;法向应力;有限元方法;荷载
中国分类号:U448.14A411494
0 引言
根据我国《2019年交通运输行业发展统计公报》显示,截止到 2019 年年末,我国公路桥梁共计 87.83×104座,总跨度已高达 6 063.46×104 m,其中特大桥梁共 5 716 座,跨度达 1 033.23×104 m;大桥共 108 344 座,跨度达 2 923.75×104 m[1]。无论从桥梁数量还是各种类型桥梁的跨度来说,我国都已成为世界第一桥梁大国。但是我国桥梁发展极不平衡,绝大多数为混凝土桥梁,钢桥或组合梁桥的占比都很少,其中钢-混组合梁桥的占比仅不足 1%[2]。钢-混组合梁桥是一种新型的桥梁体系结构,可以发挥出钢材和混凝土两种材料的优势[3-5],钢主梁和混凝土板可以通过抗剪连接件连接受力,充分利用钢和混凝土的特点,钢材的抗拉性能和混凝土的抗压性能同时发挥作用,并且钢-混组合梁桥具有自重轻、构件刚度大、抗倾覆能力、施工速度快、综合效益好等优点[6-7],分别与由钢和混凝土各自制成的结构相比,组合结构具有更高的承载能力,并减少了材料的消耗。
目前,不少国家机构都已开展了钢筋混凝土与钢筋刚性锚固组合的理论分析和试验研究。研究认为:在反复加载和卸载剪切力作用下,组合结构的静载试验显示了刚性锚固工作的非弹性性质,以及在反复荷载作用下残余剪切位移的累积[8]。在第一个加载阶段,残余位移的大小与弹性位移的数量级相同,且随着残余位移的累积,弹性变形模量呈下降趋势。在大多数情况下,承载力的耗尽是因为混凝土板的变形造成的结果。
应力集中系数[9]是结构耐久性计算的基础,是确定结构可靠度、耐久性和预测开发后剩余资源量的重要参数。本文研究对象为桥梁跨径结构的轧钢梁与钢筋混凝土路面板相结合,剪切连接器是两壁刚性锚,可感知剪切力和撕裂力。并通过理论计算,确定了大跨度组合结构梁单元长度方向上刚性锚固区的应力集中系数变化。
1 桥梁跨度结构设计模型的建立
用现有的解析计算方法很难描述单元之间的应力分布。为了解决这类问题,通常使用实现有限元方法(FEM)的现代软件和计算系统进行数值研究。因此本文利用LIRA-SAPR(有限元分析的软件)对应力集中系数进行了数值研究。
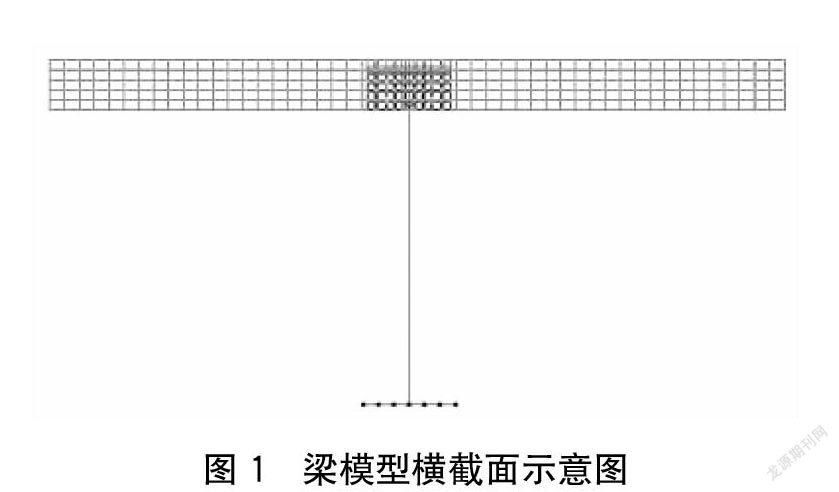
为了方便模拟,该桥梁跨度结构的支撑结构设置为90B2的工字钢截面,板截面宽为2.5 m(如图1所示)。选择截面是由于在计算机上解决所有跨度施工问题所面对的复杂性,对一个空间方案进行计算,其节点有6个自由度:3个线性位移和3个旋转角(X、Y、Z、Ux、Uy、Uz),位移由沿中间支撑轴线(禁止沿Z方向移动)和沿靠近海岸支架的梁边缘(禁止沿Z、X、Y方向运动)的连接件限制,跨度为16.76 m。
道路面板(图2)是通过体积有限元模型(34个通用的空间六节点等参有限元和36个通用的空间八节点等参有限元)进行模拟的。采用带加劲肋和锚固的跨梁(图3)来模拟壳体包络(41个通用矩形壳有限元、42个通用三角形壳有限元、44个通用四边形壳有限元)。
有限元网格的尺寸分配方式应确保获得的结果误差不超过5%,而有限元网格的特征尺寸为:
(1)水平方向50 mm;(2)垂直方向30 mm;(3)在锚固区域中,为了更详细地进行锚固建模和应力集中系数研究,对网格步长进行了压缩。
为了模拟板和梁上带之间的统一接缝,在垂直Z轴方向进一步进行了合并运动。因此,在跨接梁弯曲过程中,沿缝节点的剪力全部转移到刚性锚上,而没有考虑钢梁上带与钢筋混凝土板之间的粘结力。
2 设计模型的荷载定义
在仿真过程中,设计方案考虑了以下荷载:(1)金属和钢筋混凝土结构的自重;(2)带状荷载A15(具有相应影响线的荷载段);(3)跨距中心的A15手推车;(4)支架附近的A15手推车。
在设计模型的节点上,沿其纵轴均匀地分配自重荷载。
本文根据分析计算结果,确定了具有临时移动荷载的加载方案。在该荷载方案下,考虑模型中的最大弯曲力和剪切力:履带式手推车的A15荷载,在计算中没有考虑对获得工作量影响较小的荷载。由于本研究仅模拟了带有一根金属梁的板截面,因此需要确定A15手推车和A15条形轨道沿参考压力影响线的总荷载(图4)。
(1)临时移动荷载A15宽度上跨度施工的荷载方案;
(2)支撑压力对极限梁的影响线(偏心压缩法)。
为了确定最大跨度弯矩,将A15手推车的荷载施加在第一个跨距中心0.6 m×0.2 m的区域上,并根据跨弯矩影响线施加带状载荷(图5)。手推车车轮的轮轴位于影响线顶部的上方。
为了确定最大支撑弯矩,将A15手推车的荷载施加在第一和第二跨0.6 m×0.2 m的区域,跨距为20.0 m,并在第一、第二和第四跨施加带状荷载(图6)。
本文根据静力计算结果,确定荷载的设计组合(如表1所示),以确定力因子的最大值。
3 节点设计模型的结果分析
本文所考虑模型的法向应力分布性质完全符合监管文件《钢规》中给出的公认理论,如图7、图8所示。模拟结果中上翼缘法向应力与模拟混凝土工作的体积有限元法向应力差值能清楚地表示出来,并沿截面高度变化。应力集中系数由公式(4)确定:
为了确定应力集中系数,如表2所示总结了第一个跨度中获得的所有法向应力(锚附近和锚之间)。发现在第一跨度中出现了弯矩和剪切力,以及剪切力的最大值(图9、图10)。
4 结语
(1)在1#锚附近以及1#和2#锚之间,混凝土板中法向应力的最大差值为37.5%。
(2)混凝土板中法向应力的最小差值(0.78%)是在最大弯矩处16#锚的区域内确定的。
(3)在连续梁体系中法向应力沿车道板宽度的不均匀分布比相同跨度的劈裂体系更为明显。通过板宽度的最大应力不均匀性出现在连续梁的支撑(包括中间支撑)上方。
(4)模拟混凝土工作时,上翼缘法向应力与体积有限元法向应力的差值能被清楚地表达出来,并且沿截面高度变化。在压缩区域中,差值为80%~85%,在拉伸区域中,差值为75%~80%。
(5)本文的研究结果可作为确定弹性应力集中系数工程方法的补充,并在将来可用于桥梁钢-混凝土结构的耐久性计算,以及预测桥梁结构的剩余寿命。
参考文献:
[1]张 坤.移动车辆荷载作用下钢-混组合梁桥动力性能研究[D].哈尔滨:哈尔滨工业大学,2020.
[2]吴建伟,蒋 蕾,徐 辉.钢-混组合连续梁桥施工与控制分析[J].工程技术研究,2020,5(17):23-25.
[3]戴晓春,王应良,游励晖,等.跨大型铁路编组站钢-混组合梁斜拉桥体设计[J].高速铁路技术,2018,9(5):48-52,83.
[4]黄 超.基于钢结构的大跨径变宽钢混组合梁施工技术研究[J].湖南交通科技,2019,45(1):117-119,124.
[5]刘 双,聂玉东,张 铭,等.钢-混组合梁斜拉桥现浇混凝土桥面板关键设计技术研究[J].公路,2020,65(7):359-363.
[6]郭增伟,陈汉林,李龙景,等.钢混组合曲线梁桥混凝土桥面板应力空间分布特性[J].沈阳建筑大学学报(自然科学版), 2019,35(4):586-593.
[7]付 彦,刘江华,汤文达.基于中外规范的钢混组合梁有效翼缘宽度影响因素分析[J].公路交通科技(应用技术版),2018,14(12):232-235.
[8]曹明明,陸 阳,黄晚清,等.复合式路面层间界面剪切滑移特性[J].交通运输工程学报,2018,18(4):1-11.
[9] 刘永健,姜 磊,熊治华,等.加劲型矩形钢管混凝土受拉节点热点应力集中系数计算方法[J].交通运输工程学报,2017,17(5):1-15.
3957501908208

