考虑黏聚力的加筋挡墙筋材内力分析方法

张飞，温友鹏，陈延博，贾世林

(1.河海大学岩土力学与堤坝工程教育部重点实验室，江苏南京，210024；2.河海大学江苏省岩土工程技术工程研究中心，江苏南京，210024)

土工合成材料加筋土挡墙是一种轻型支挡结构，具备施工装配性、生态环保性和抗震性等诸多优势[1−2]，在国内外工程中得到广泛应用。根据现行加筋土挡墙设计规范[3−6]，安全设计主要包括内部稳定性分析、外部稳定性分析、复合破坏模式与面板连接安全校核[7−9]。内部稳定性是加筋土挡墙安全设计的关键，筋材内力计算又是内部稳定性分析[10−12]的核心，但现有筋材内力的计算多局限于加筋区内筋材的抗拔破坏。

加筋土挡墙筋材内力计算方法主要有主动土压力理论[3−6]、极限平衡法[13]、K刚度法[14]、基于非线性弹性理论与变形协调的E-M法[15]和非线性弹性增量法[16]。目前加筋土挡墙设计规范主要采用较简单的朗肯/库仑土压力理论分析内部稳定性，但计算的筋材内力远大于实测的筋材内力[17−19]。为此，ALLEN 等[14]基于大量实测数据进行回归统计，提出了工作状态下的筋材内力计算方法(即K 刚度法)。E-M 法[15]基于土体与筋材应变相容理论充分考虑了筋土协调变形，但没有考虑填土横向变形与应力之间的非线性关系，LIU[16]针对此问题，基于填土泊松比随应力不断变化，考虑填土横向变形与应力之间的非线性关系，改进了E-M 法提出了一种计算筋材内力的非线性弹性增量方法。规范要求加筋土挡墙的填土应使用排水性良好的无黏性土，然而在我国偏远山区，加筋土结构的填土主要就地取材，不可避免地采用含部分细粒填土，导致填土具有一定黏聚力[20]，在加筋土挡墙筋材内力计算中需要考虑填土黏聚力的影响。

LESHCHINSKY等[21−23]基于极限平衡理论采用库仑直线和对数螺旋线破坏模式，提出了加筋土结构极限状态下筋材内力逐层计算方法，在计算筋材内力分布时考虑筋材前端和后端抗拔强度，并计算面板连接强度。本文作者在其基础上，针对模块式面板土工格栅加筋土挡墙，考虑填土黏聚力对筋材内力的影响，开展参数敏感性分析，揭示填土强度、墙面倾角及筋材长度对加筋土挡墙筋材力学性状与变形特性的影响。

1 加筋土挡墙筋材内力计算方法

1.1 基于转动破坏机制的极限平衡理论

已有研究[24−26]表明，无黏性加筋土挡墙加筋区内的破坏多为直线平动形式，而采用黏性土填筑的挡墙内则会呈现转动破坏模式，故本文采用对数螺旋线转动破坏机制进行分析。图1所示为典型的加筋土挡墙简化模型，其中：H为墙体高度，ω为墙面的垂直倾角，L为筋材长度，Sv为筋材铺设间距，n为加筋层数，c为填土黏聚力，φ为内摩擦角，γ为重度。对数螺旋线破坏面r(β) 在极坐标系下表示为

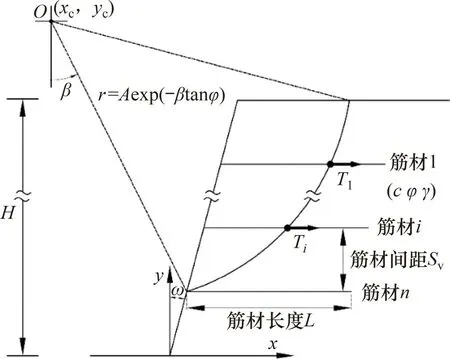
图1 加筋土挡墙简化分析模型与破坏模式Fig.1 Simplified model and failure mechanism of reinforced soil retaining wall

式中：A为常数；β为极径r与垂直线间的夹角，极点即转动中心为点O(xc，yc)。

为了计算极限状态下加筋土挡墙的筋材内力，这里有以下假设：

1)所有可能的滑动面均为对数螺旋线形，且只通过加筋区及其背部土体，不考虑穿过挡墙底部的深层滑动；

2)填土为各向同性的均质土体，忽略孔隙水压力作用；

3)筋材发挥的拉力始终为水平方向；

4)筋材的抗拉性能可以被完全调动，且不超过筋材的极限抗拉强度；

5)面板本身不发生破坏，忽略面板−面板间摩擦作用、面板−填土间摩擦作用以及墙趾对加筋土挡墙稳定性的影响[27−28]；

6)极限状态是一种理想状态，各处土体均先达到强度临界状态，考虑因筋土界面摩擦强度不足发生的筋材拔出破坏来确定筋材内力；

7)填土强度采用摩尔−库仑破坏准则，认为滑动体为刚性，忽略加筋土结构发生滑移引起的填土与筋材的相对位移，土体和筋材变形均不予考虑。

基于对数螺旋线滑动面建立围绕转动中心的力矩平衡方程，其中对数螺旋滑动面上正应力与抗剪力摩擦分量的合力始终通过转动中心，此时不需要计算滑动面上正应力产生的力矩。在力矩平衡中，滑动力矩只需要考虑土体自重的滑动力矩、土体黏聚力提供的抗滑力矩、筋材提供的抗滑力矩。

式中：MT为筋材提供的抗滑力矩；Mc为土体黏聚力提供的抗滑力矩；Mw为土体自重产生的滑动力矩，具体表达式推导参见文献[23,29]。

1.2 筋材内力分布逐层计算

本文方法不仅考虑滑动面穿过加筋体的情况，还考虑滑动面部分穿过加筋体的复合破坏模式，这可能会引起筋材后端内力较大，超过筋材后端抗拔强度。筋土之间的相互作用机制复杂[30]，为了简化分析，这里根据筋土界面摩擦特性[22−23]，筋材后端抗拔强度Tendpo-i可表示为

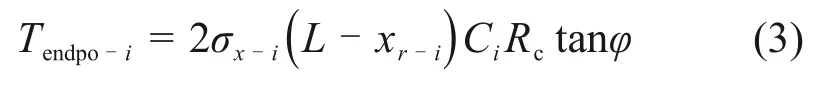
式中：xr−i为筋材某点距墙面的水平距离；σx−i为该位置处的上覆压力；Ci为筋土界面摩擦因数；Rc为筋材覆盖率。

图2所示为筋材内力分布曲线与其前后端抗拔强度包络线关系。由图2可见：过长的筋材长度可以使筋材内力的充分发挥，理想筋材长度使筋材内力分布曲线与抗拔强度包线相切，过短的筋材长度使筋材内力的发挥受限于后端抗拔强度。因此，在逐层计算筋材内力分布时，当有筋材所需拉力超过其后端抗拔强度，需将其拉力更新为可发挥的后端抗拔强度，同时将更新后的拉力代入力矩平衡方程重新计算滑动面穿过的较下层筋材对应位置的所需拉力。若没有较下层来承担拉力，则此时的筋材长度等参数设置不合理，需重新设计计算。

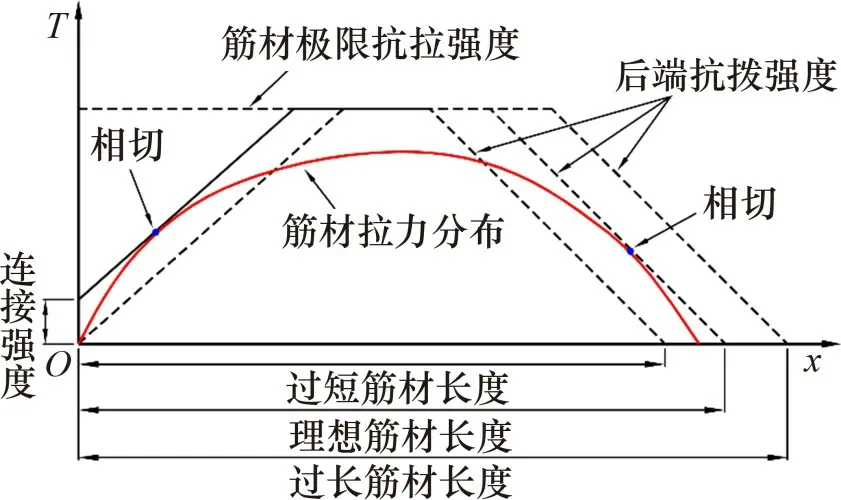
图2 筋材内力分布与其前后端抗拔强度包络线关系Fig.2 Relationship of reinforcement load distribution and front and rear pullout envelope

筋材前部自由端的抗拔强度与后端抗拔强度一致，若筋材前端内力超过前端抗拔强度，则需要墙面的面板提供一定的连接强度To−i来防止面板−筋材连接失效。此时，筋材前端抗拔强度可表达为

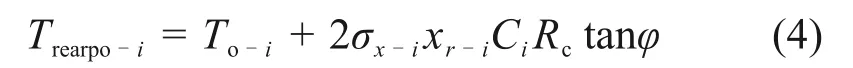
式中：To−i为第i层筋材处墙面板所需提供的连接强度，当筋材筋材内力分布曲线与其前端抗拔强度包络线相切时最理想，此时前端抗拔强度包络线的纵轴截距即为筋材所需的最小面板连接强度(见图2)。

运用HAN 等[22]提出的方法可获得极限平衡状态下加筋土挡墙的筋材内力分布，其核心思路为：

1)计算第i层筋材所需加筋力时，以第i层筋材以下所有筋材与面板交点以及墙趾作为滑出点，搜索所有可能穿过第i层筋材的滑裂面。针对任意一个可能的滑裂面，根据滑动体力矩平衡计算出筋材内力。将筋材分为若干单元，将内力储存在滑裂面穿过单元内。

2)在自上而下的计算过程中，筋材单元内力保留较大值，在更新单元内力时需要始终使滑裂面对应的滑动体满足力矩平衡。利用式(3)计算各层筋材中各个单元处的后端抗拔强度，比较每个单元的后端抗拔强度与筋材内力，若筋材内力更大，则令此单元的筋材内力等于后端抗拔强度，并将大于的部分分配给同一滑裂面上的下部筋材承担，保证同一滑裂面上内力满足式(3)；反之说明满足后端抗拔要求，保持此单元筋材内力不变。

3)根据式(3)计算前端抗拔强度，并调整前端抗拔强度线使其与筋材内力分布曲线相切，此时前端抗拔强度曲线的截距即为稳定所需的面板−筋材连接强度(图2)。

根据上述筋材内力计算步骤绘制计算流程图，如图3所示。

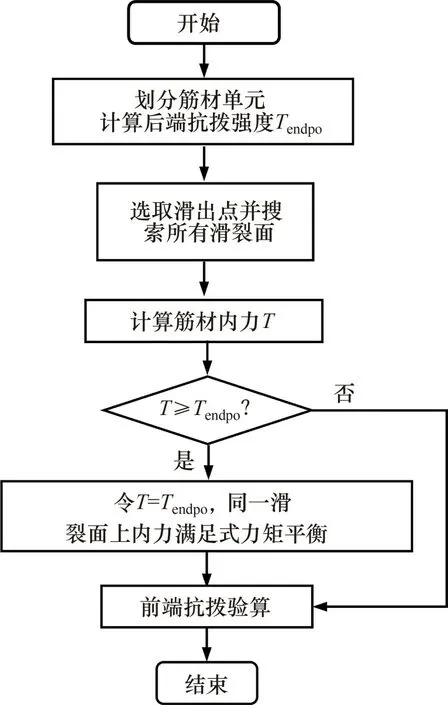
图3 加筋土挡墙筋材内力计算流程图Fig 3 Flow chart of reinforcement tensile load of GRS wall

1.3 计算结果的验证

基于上述计算方法编制相应的计算程序，为了验证本文方法与相应程序计算结果的可靠性，以KANG[29]中的算例进行对比分析。该算例加筋土挡墙高度H=6 m，加筋长度L=4.2 m，加筋间距Sv=0.6 m，填土重度γ=20 kN/m3，填土黏聚力c=0 kPa，填土内摩擦角φ=36°，筋材覆盖率Rc=1.0，加筋土界面摩擦因数Ci=0.8，分别考虑2种墙面倾角ω为0°和20°进行计算，结果如表1所示。

从表1可见：本文计算结果与KANG[29]计算结果基本一致，仅有ω=20°情况下的To−i差别较大。产生这种差别的原因在于非直立墙面情况下，筋材前端内力计算时考虑滑动面滑入点角度约束。一般认为土体没有抗拉强度，滑动面的滑入处不会出现悬垂现象[31]，故需要限制潜在滑动面的滑入点切线与水平线夹角θ2。确定筋材内力分布时需要考虑所有可能的滑动面，如果滑动面的滑入点发生在倾斜的墙面上，这时有2 种限制方式，如图4所示：1)以滑动面在墙顶高度的位置点进行悬垂限制；2) 以滑动面在墙面滑入点进行悬垂限制。KANG[29]计算时采用了第1 种方式进行悬垂约束，过大限制夹角θ2致使筋材前端稳定所需的加筋力偏小，这样确定的筋材与面板的连接强度To−i就会较小。本文对此进行修正，采用第2种方式来确定筋材与面板连接强度。

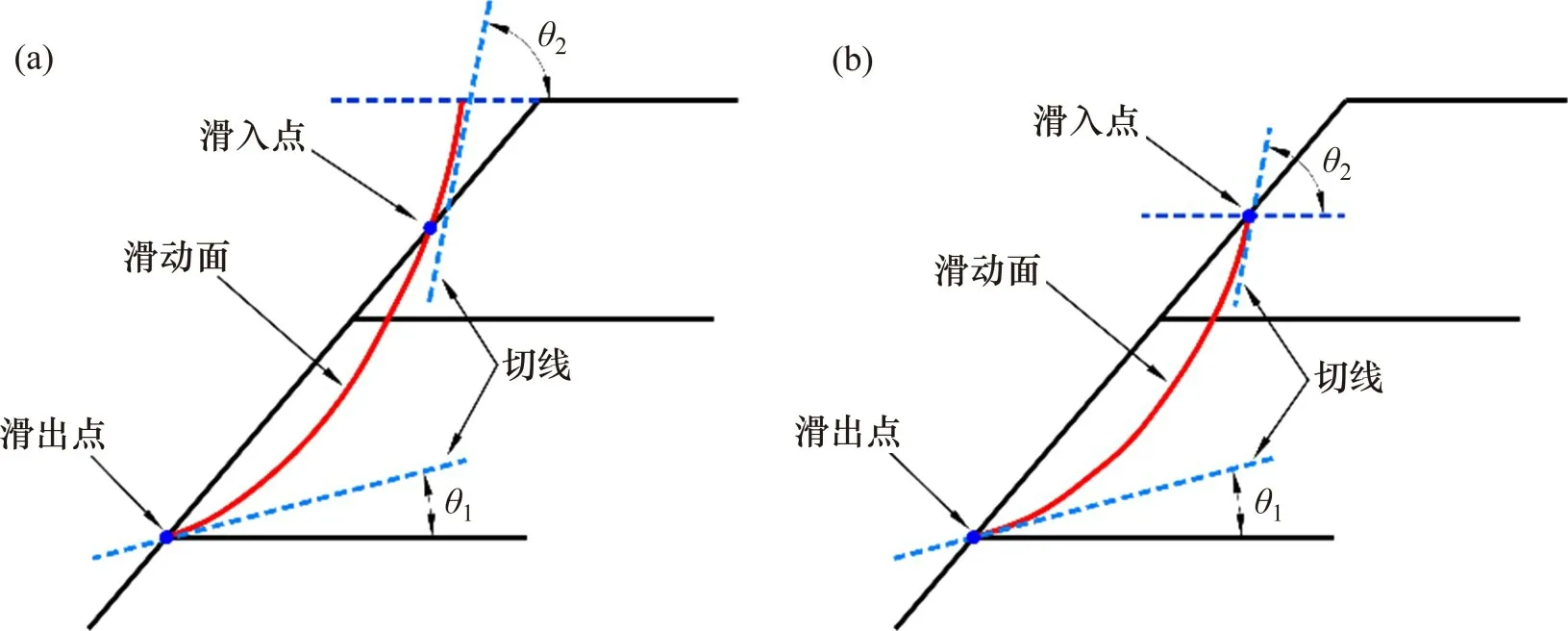
图4 对数螺旋线滑面的规定Fig.4 Defined trace log-spiral slip surface

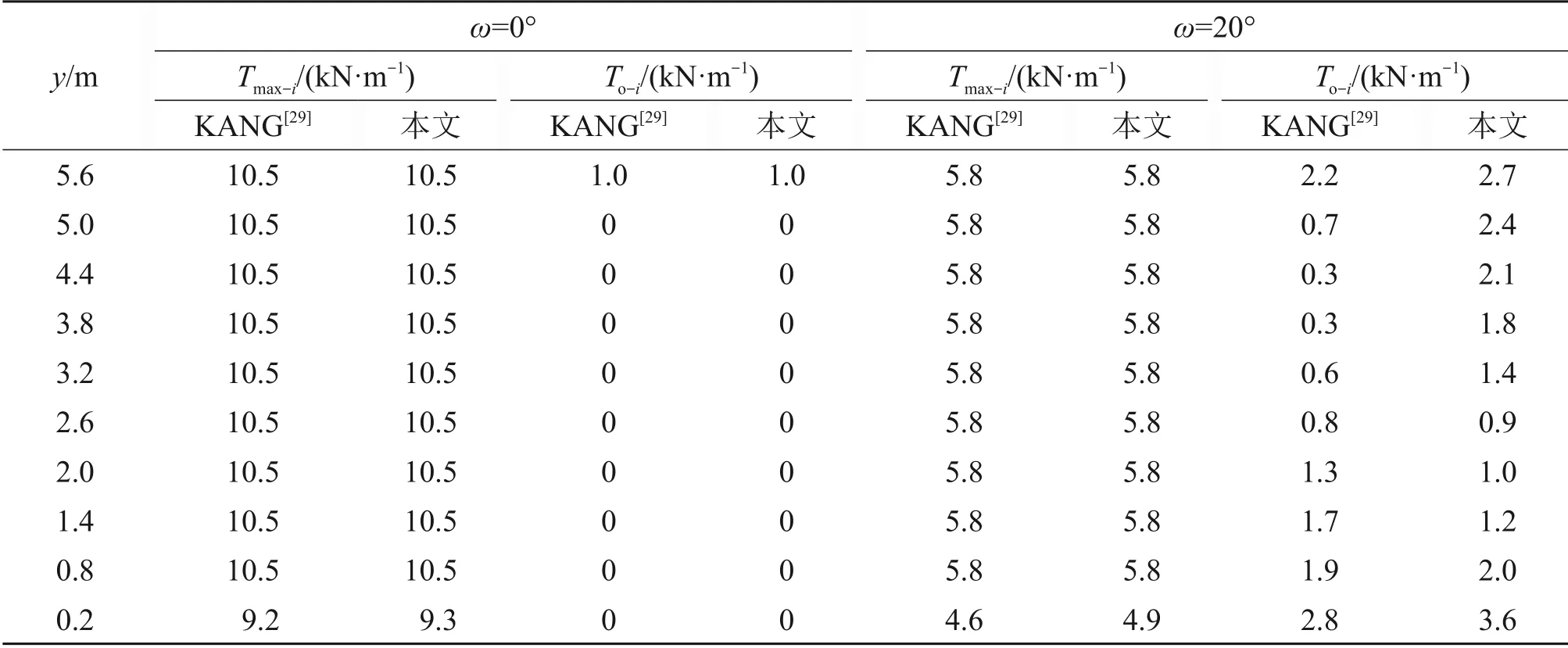
表1 算例Tmax和To的计算结果对比Table 1 Comparison of calculated results Tmax and To for given examples

YANG等[32]运用离心机开展了加筋土陡坡破坏模型试验，获得了极限状态下的滑动面及其对应的离心加速度，并将结果与极限平衡法和有限元法进行对比。本文针对其给出的2个不同密实度加筋陡坡模型M1和M3进行分析。其模型参数如下：坡高H=228.6 mm，坡率为1.0:0.5，加筋长度L=203 mm，加筋间距Sv=25.4 mm；M1 模型的填土重度γ=16 kN/m3，内摩擦角φ=42.2°，M3模型的填土重度γ=15.7 kN/m3，内摩擦角φ=39.1°。

图5所示为不同分析方法潜在滑动面对比。由图5可见：几种方法确定的最危险滑动面位置十分接近，本文分析方法确定的滑动面仅在上部相比其他结果更为靠近筋材前端。因此，本文所提出的加筋土结构极限状态筋材内力分析方法是可靠的，可以较好地预测最危险滑动面。

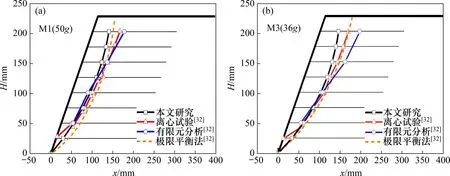
图5 不同分析方法潜在滑动面对比Fig.5 Comparison of potential sliding surface of different analysis methods

2 极限状态下加筋土挡墙力学性状的影响规律

运用上述计算方法分析加筋土挡墙力学性状影响规律，这里重点考虑的设计参数为填土抗剪强度c、内摩擦角φ、墙面倾角ω和筋材长度L。

2.1 不同填土抗剪强度的加筋土挡墙力学性状

加筋土挡墙大多要求采用无黏性土作为填土，保证其良好的透水性，然而在施工质量控制与排水系统有效设置下，允许填筑部分细粒土，这使得填土具有一定黏聚力。填土抗剪强度会直接影响加筋土挡墙的土体抗滑力矩，土体内摩擦角还会影响筋材的前后端抗拔强度。参数分析模型中的参数取值依据相关规范及工程经验，如图6所示。

图6 分析参数取值Fig.6 Parameters of analysis

图7所示为加筋土挡墙极限状态下不同填土强度下各层筋材最大内力Tmax和面板连接力To的计算结果。由图7可见：随着填土抗剪强度c和φ增大，土体能提供的抗滑力矩增大，导致To和Tmax显著减小，较小的黏聚力(5 kPa)即可减少约1/3 筋材拉力。当填土内摩擦角大于30°时，由于加筋长度足够长，使各层筋材内力可以充分均匀发挥，且稳定所需面板连接力很小，只有填土为无黏性土时最上层筋材需要较大连接强度。

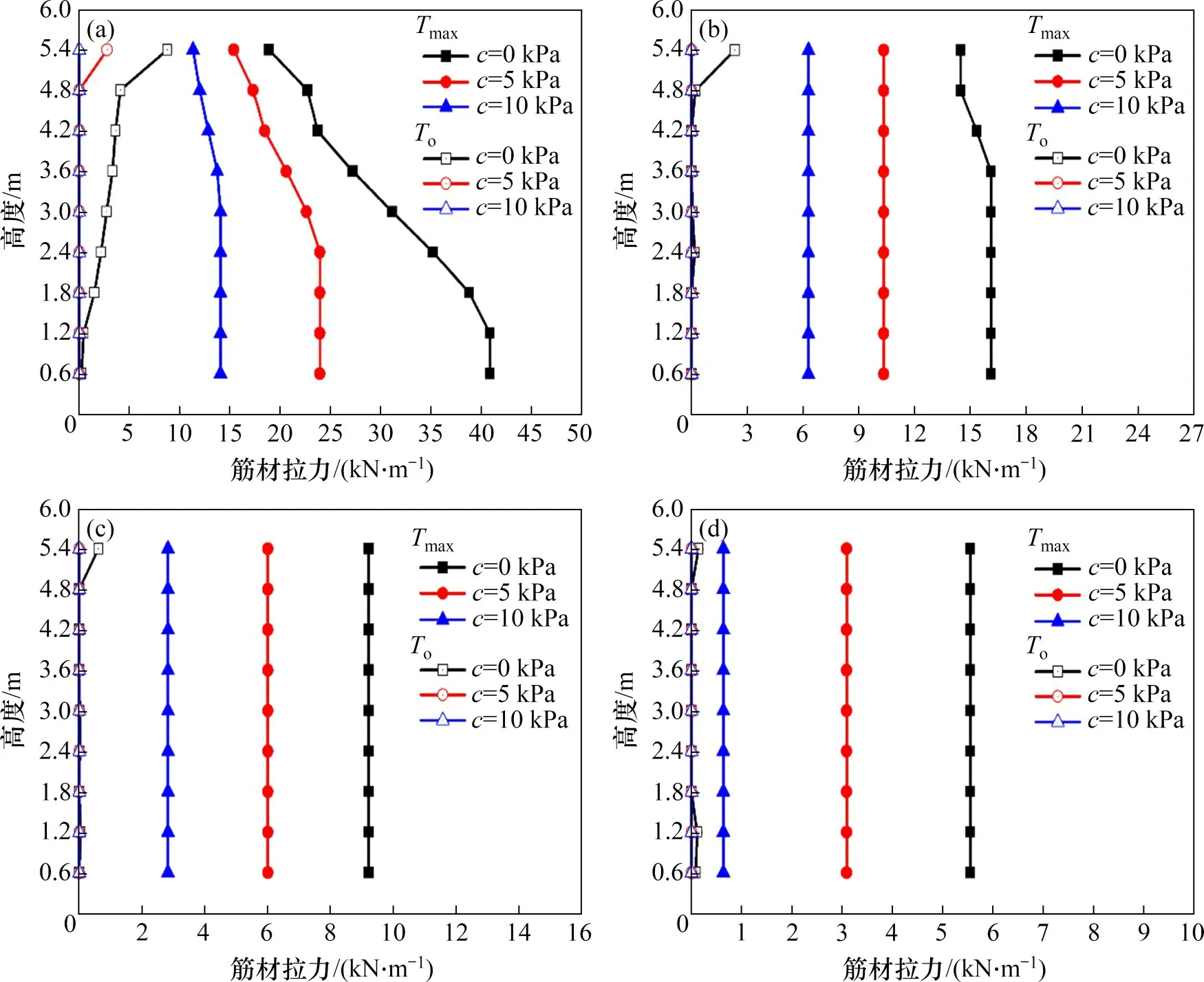
图7 填土强度对极限状态加筋土挡墙To和Tmax的影响Fig.7 Influence of backfill shear strength on To and Tmax

图8所示为当c为0 kPa 时各层筋材内力与前端抗拔强度分布曲线。结合式(4)可知，筋材的前端抗拔强度线的斜率随上覆荷载减小而变缓，因此越靠上的筋材需要越大的面板连接力To以保证面板−筋材的连接稳定性。

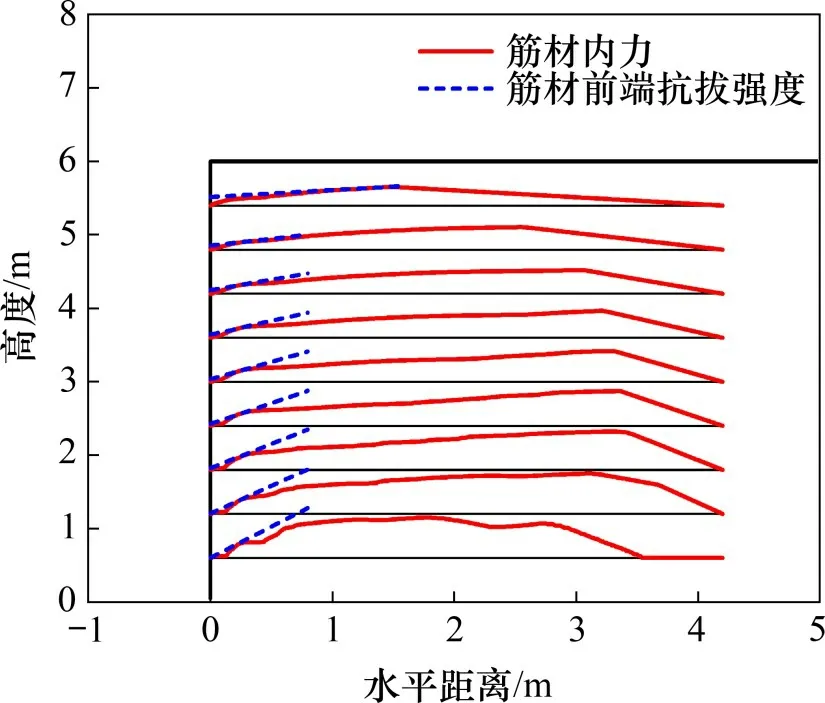
图8 筋材内力与前端抗拔强度分布Fig.8 Distribution of reinforcement loads and front available pullout resistance

加筋土挡墙的最危险潜在滑裂面可用Tmax位置表征，填土强度对极限状态下加筋土挡墙Tmax位置的影响如图9所示。由图9可见：挡墙破坏模式随填土内摩擦角增大从复合破坏转变为内部稳定性破坏，且黏聚力对Tmax位置的影响变小。当土体内摩擦角为20°和30°时，挡墙上部筋材Tmax位置随黏聚力增大而偏离墙面，而挡墙下部正好相反。为解释此现象，图10给出了图9工况下的筋材内力分布与Tmax位置。

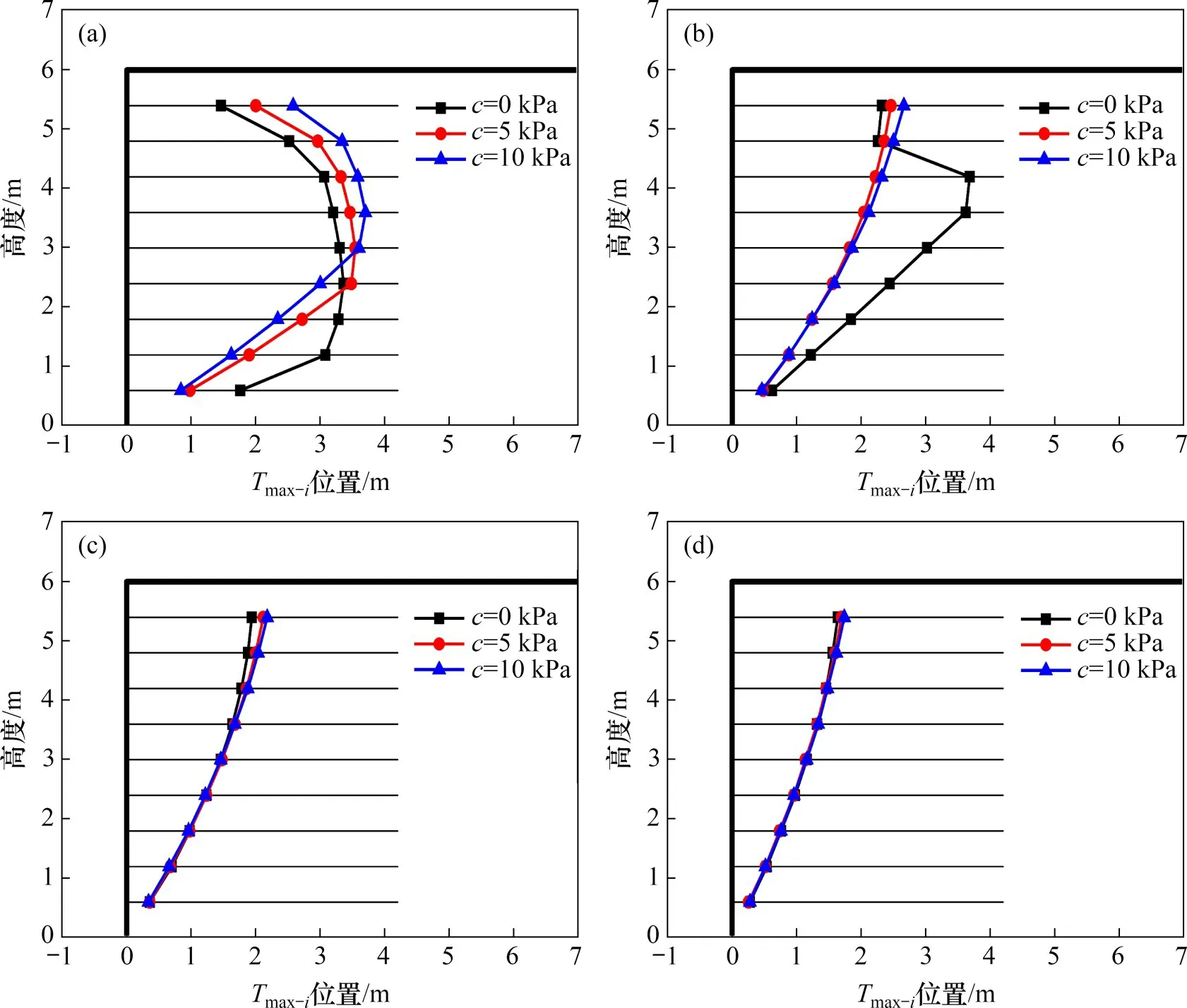
图9 填土强度对极限状态加筋土挡墙Tmax位置的影响Fig.9 Influence of backfill shear strength on position of Tmax

由图10可见：挡墙下部Tmax位置主要受破坏模式控制，增加黏聚力提供的抗滑力矩使滑动面更加靠近墙面。而挡墙上部筋材最大内力Tmax受到后端抗拔强度的限制，增加填土黏聚力可以减少筋材内力但不影响后端抗拔强度，最终导致Tmax位置向筋材后端移动。当土体内摩擦角为30°时，随黏聚力增大，挡墙由复合破坏模式变为内部稳定性破坏。对于黏性土挡墙，上层筋材前端存在零拉力段，且该段随黏聚力增大而增大，这抑制了上层筋材后端内力发挥，导致Tmax位置偏离墙面。

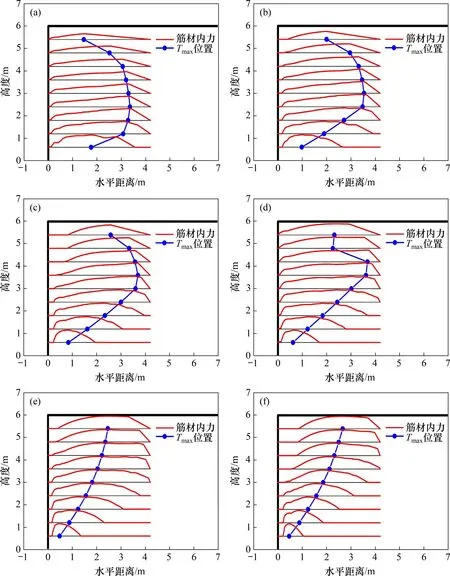
图10 填土强度对筋材内力分布与Tmax位置的影响Fig.10 Influence of backfill shear strength on distribution of reinforcement loads and position of Tmax

土工格栅加筋土挡墙具有柔性特点，允许产生一定侧向变形，但过大变形会影响加筋土挡墙的稳定性。结合极限状态下筋材内力分布可以估算其墙面的水平位移。墙面水平位移可通过各筋材的累积变形来估算：

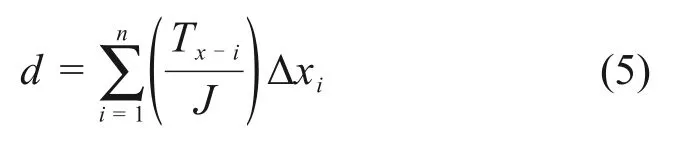
式中：d为墙面板位移，m；Tx−i为筋材某微段对应所需拉力，kN；Δxi为微段长度，m；J为筋材刚度，kN/m，这里取500 kN/m。这种简化加筋土结构水平变形的计算方法仅考虑了筋材的线弹性变形，没有考虑土体和筋材及其相互作用变形特性[33−37]，不能准确计算加筋土挡墙产生的变形，无法很好地考虑筋材刚度的影响，这里计算结果仅作为极限状态下加筋土挡墙的变形特性研究(如最大水平变形位置、墙面变形特征等)。

图11所示为不同抗剪强度下加筋土挡墙的墙面水平位移。由图11可见：随着填土内摩擦角φ减小，墙面位移分布形式逐渐从“顶部大底部小”变为“中部大上下两端小”，出现明显的鼓胀现象，现场监测结果[38−39]也发现加筋土挡墙的墙面存在鼓胀变形。使用黏性填土可以有效地减少墙面位移，缓解墙面鼓胀变形。当工程中采用内摩擦角较小的填土填筑加筋土挡墙时，应考虑使用具有一定黏聚力填土来提高挡墙稳定性并减小墙面侧向变形。

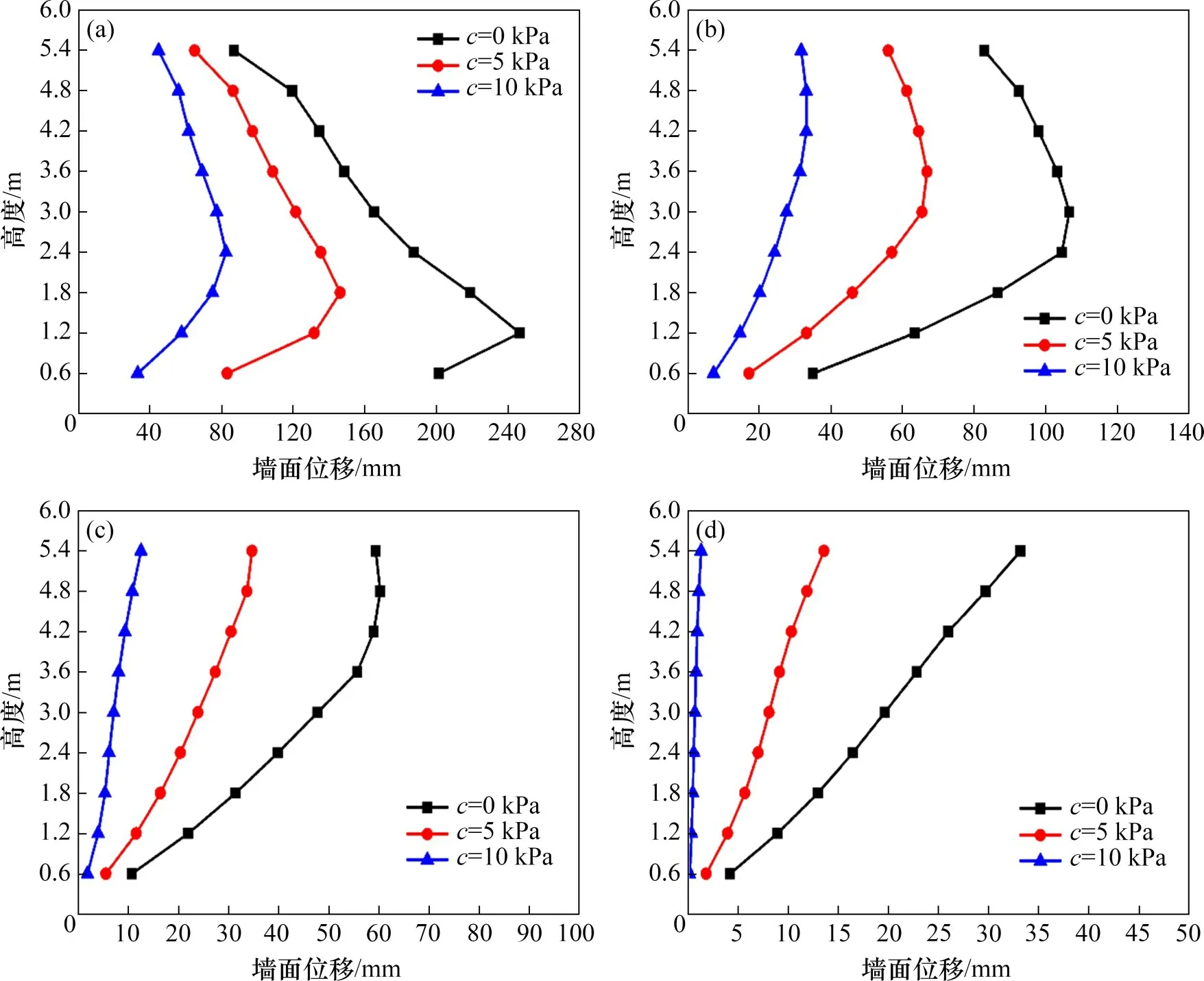
图11 填土强度对极限状态加筋土挡墙墙面水平位移的影响Fig.11 Influence of backfill shear strength on horizontal displacement of GRS wall

2.2 不同墙面倾角的加筋土挡墙力学性状

通过加筋土技术可以实现近乎直立的挡墙或陡坡形式，满足填土空间的限制条件。采用2.1算例相同的参数，分析不同墙面倾角ω对各加筋层Tmax和To的影响规律，图12给出了ω为0°，10°，20°和30°时各加筋层Tmax和To计算结果。由图12可见：随着墙面倾角ω增大，Tmax显著减小。值得注意的是，当填土为内摩擦角很小的无黏性土时(图12(a))，挡墙下部Tmax随ω增大而增大。To整体呈现“中间小两端大”的分布特点，且挡墙顶部To随ω增大而增加，下部To随ω增大而减小。当墙面倾角为10°时，面板连接强度整体大于其他角度的面板连接强度，实际工程中需要注意。

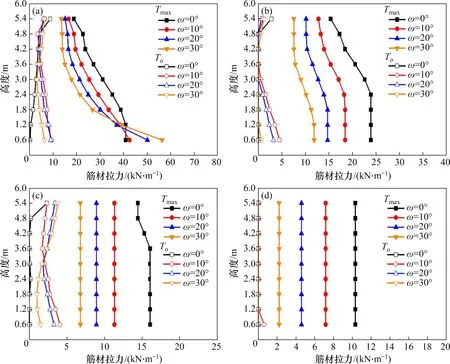
图12 墙面倾角对极限状态加筋土挡墙To和Tmax的影响Fig.12 Influence of wall inclination on To and Tmax

图13所示为在不同墙面倾角下加筋土挡墙的墙面水平位移情况。由图13可见：增大墙面倾角可以显著减少墙面侧向变形，10°的墙面倾角可以减小墙面最大水平位移约1/4。增大墙面倾角可以减轻墙面鼓胀变形，有利于加筋土挡墙的侧向变形控制。

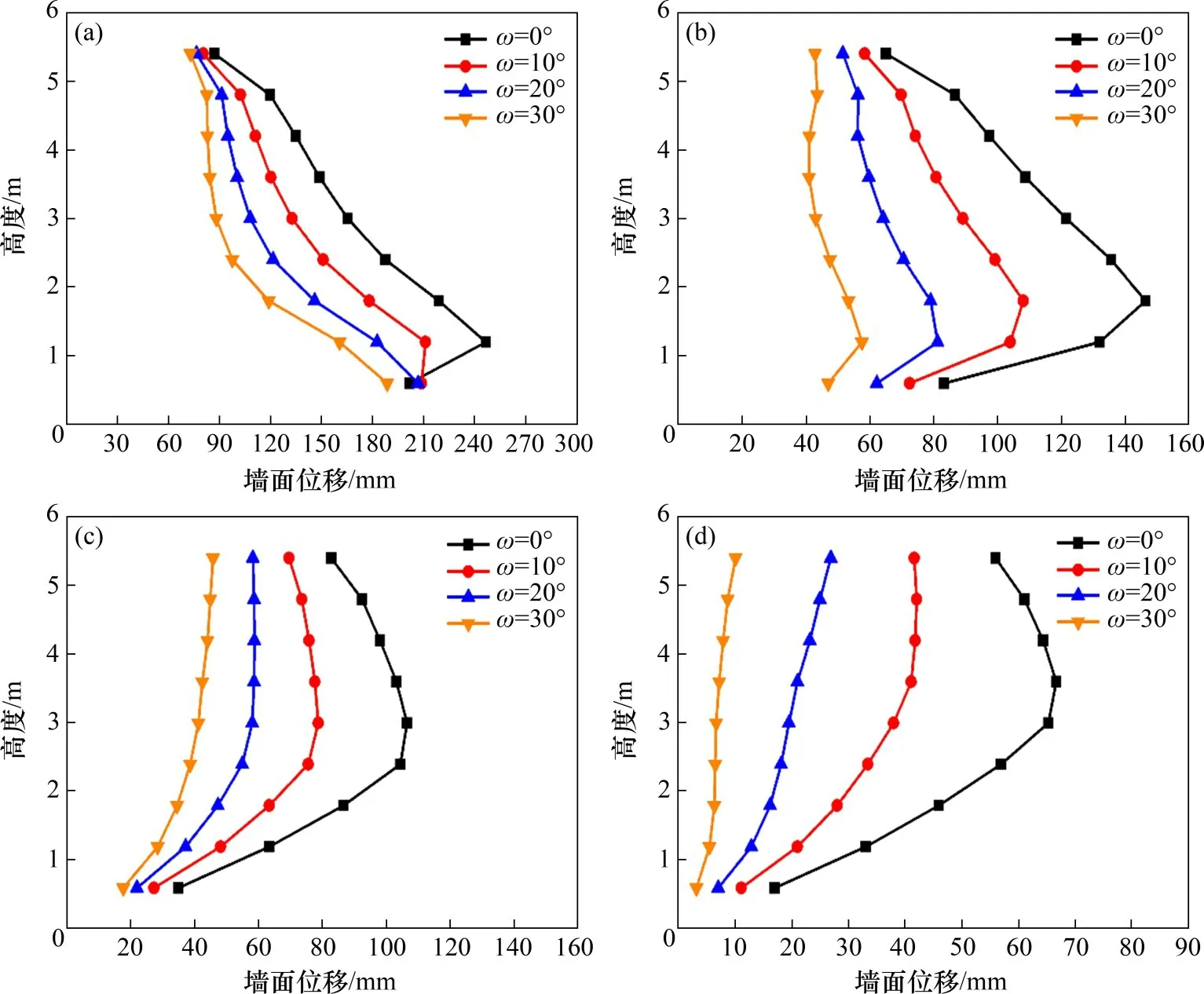
图13 墙面倾角对极限状态加筋土挡墙墙面水平位移的影响Fig.13 Influence of wall inclination on horizontal displacement of GRS wall

2.3 不同筋材长度的加筋土挡墙力学性状

加筋土挡墙的加筋力主要通过筋土界面摩擦发挥作用，安全设计要求筋材不发生拔出破坏，只有筋材长度足够才能提供充裕的后端抗拔强度。通常加筋土挡墙设计要求筋材长度至少为0.7倍墙高H，这里考虑3 种筋材长度(0.5H，0.7H以及1.0H)，分析不同筋材长度对加筋土挡墙(H=6 m，φ=20°，ω=0°)力学性状的影响规律，如图14所示。由图14可见：筋材长度对To几乎没有影响，对Tmax影响较大。当筋材足够长时，各层筋材Tmax沿墙高均匀分布。当筋材过短时，上层筋材被拔出，挡土墙发生复合破坏，导致下部筋材Tmax显著增加。采用有一定黏聚力的填土，可以显著减少下层筋材所需拉力，使得各层筋材拉力可以更均匀地发挥。

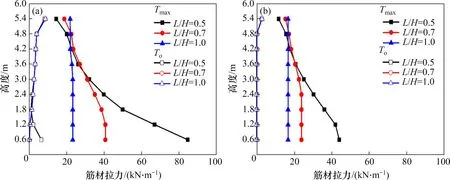
图14 筋材长度对极限状态加筋土挡墙To和Tmax的影响Fig.14 Influence of reinforcement length on To and Tmax

图15所示为筋材长度对Tmax位置的影响。由图15可见：当筋材长度较短时，上层筋材所能发挥的加筋力受抗拔强度的影响较大，Tmax位置明显向墙面方向偏移，而中下层筋材受复合破坏模式影响，Tmax位置则偏向筋材后端。

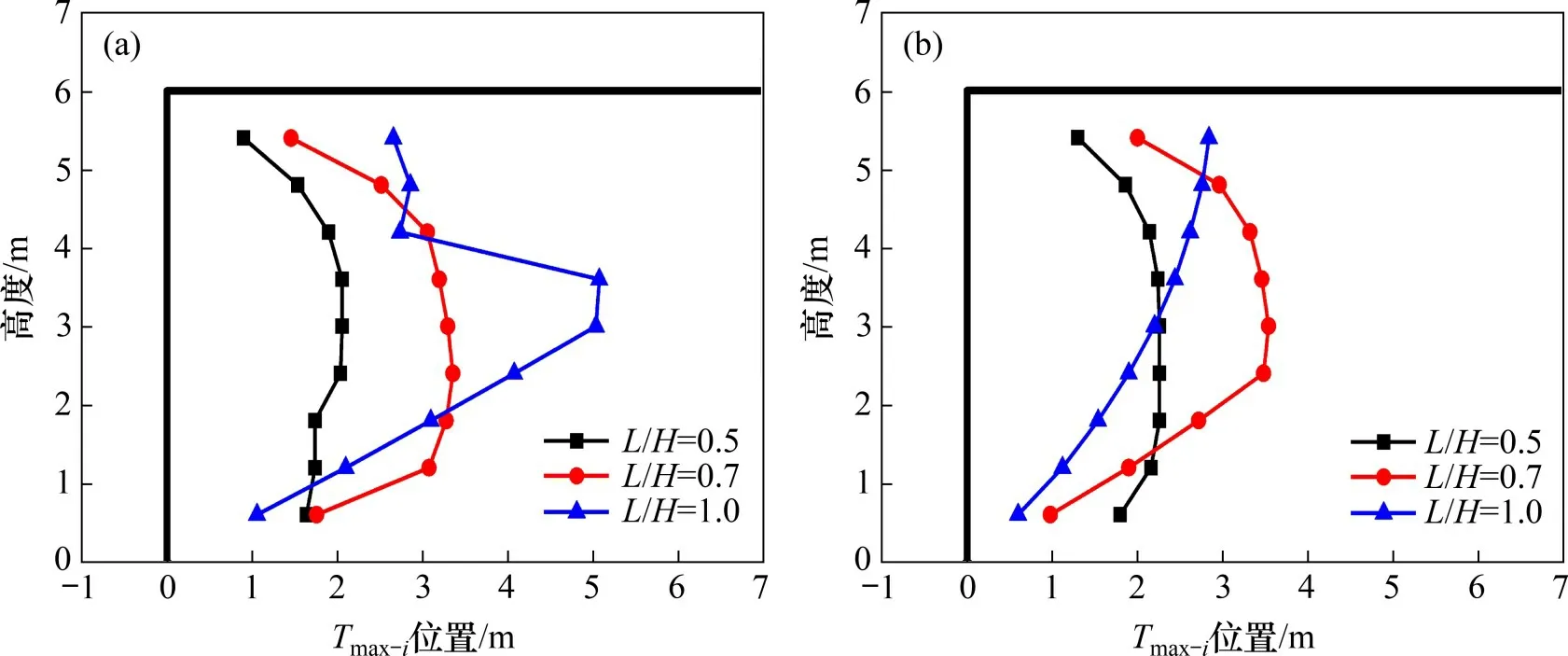
图15 筋材长度对极限状态加筋土挡墙Tmax位置的影响Fig.15 Influence of reinforcement length on position of Tmax

图16所示为筋材长度对极限状态加筋土挡墙墙面水平位移的影响。由图16可见：填土的黏聚力可以有效减少墙面侧向变形。当筋材长度较长时，墙面位移呈“中间大两端小”的分布。当筋材长度较小时，筋材内力分布受明显受到后端抗拔强度的限制，上层筋材能承担的拉力有限，导致下层筋材内力增大，使墙面位移呈“上小下大”的分布。

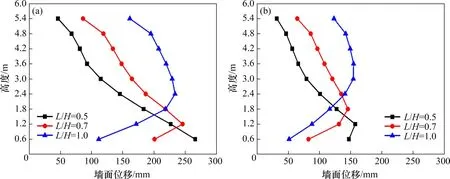
图16 筋材长度对极限状态加筋土挡墙墙面水平位移的影响Fig.16 Influence of reinforcement length on horizontal displacement of GRS wall

3 结论

1)加筋土挡墙采用黏性土作为填土能减小筋材内力和墙面侧向变形，很小的黏聚力(5 kPa)就可以大幅降低稳定所需的筋材拉力(约1/3)和墙面水平位移。采用较小内摩擦角的黏性土作为填土会导致挡墙中下部出现鼓胀变形，此时最危险滑动面为部分穿过加筋区的复合破坏模式，因而建议工程中尽量选用内摩擦角较大的黏性土作为加筋挡墙填土。

2)相比直立挡墙情况，墙面倾斜显著减小稳定所需的筋材拉力和墙面水平位移，同时减少墙面可能发生的鼓胀变形，但微小的墙面倾角(约10°)会增大挡墙下部面板与筋材的连接强度。

3)缩短筋材长度会增加挡墙中下部筋材拉力和侧向变形量，工程中应在挡墙下部采用极限抗拉强度更高的筋材，或者选择黏性土作为填料减小挡墙筋材拉力和水平位移。

4)本文研究结论基于一加筋土挡墙简单算例，以后可以结合实际工程运用本文方法开展更复杂的加筋挡墙筋材内力分析，从而指导工程的安全设计与变形控制。此外本文所采用的面板侧向位移计算方法忽略了土体本身及筋土间的相对位移，还有待进一步完善。