基于梁格林函数的有砟轨道高频振动响应特性分析

袁可琢，成功，韩健，肖新标

(1.西南交通大学牵引动力国家重点实验室，四川成都，610031；2.西南交通大学机械工程学院，四川成都，610031)

当列车在轨道上运行时，轮轨间的不平顺会导致轨道系统的垂向振动，且由于非连续支承和结构变形等，轨道的力学行为表现出高频振动[1]，这种振动对轨道本身十分不利。对于轨道的振动响应问题，国内外学者从不同方面进行了研究，其中模态叠加法是较为成熟的研究轨道响应的解析方法，SUN等[2]基于模态叠加法建立了轨道模型以研究道砟沉降对车辆/轨道系统的影响。理论上，模态叠加法为无限个结构模态的线性叠加，在实际应用中需考虑边界条件的影响，合理地选取轨道长度和模态截断频率，以确保计算的精度和效率。波传播法[3]是另一种常用的解析方法，其将轨道的空间响应表达成指数函数的形式，通过其所需满足的边界条件求解复波数和幅值，并最终得到轨道响应。波传播法求解过程的物理概念清晰且满足更多的边界约束条件。利用解析法通常需要将钢轨简化成梁模型[4−8]，在满足一定精度的前提下可以在很大程度上提高计算效率，且相较于Euler 梁模型，Timoshenko 梁模型能更好地反映钢轨高频特性[9]。

随着商业软件的成熟，有限元法因其较高的计算精度而成为研究轨道响应的重要方法。任娟娟等[10]利用ANSYS 对CRTS III 型板式无砟轨道进行了谐响应分析，给出了轨道结构参数的优化建议。李志强等[11]借助LS DYNA3D建立了车辆/轨道系统的有限元模型，研究了冲击载荷作用下的轮轨系统动态响应。辛欣等[12]通过ANSYS 和多体动力学软件SIMPACK的联合仿真提高了研究轨道结构振动的效率。当需要考虑更高频段或引入较长的轨道模型时，随有限元网格数量增加，其计算效率会大程度降低。为此，人们发展出了介于有限元法和解析法之间的2.5D 有限元法[13−14]。ZHANG等[15]利用2.5D有限元法研究了轨道系统的频域动态响应，并与包含不同刚度扣件的轨道测试结果进行了对比分析。与有限元法一样，2.5D有限元法可以考虑钢轨的截面变形，不仅扩大了其在高频的适用范围，还在一定程度上解决了有限元法计算效率低的问题。

格林函数法也被广泛应用于轨道振动响应问题的研究。孙宇等[16−17]在考虑车辆−轨道垂向相互作用时应用了格林函数法，其中钢轨的格林函数仍是通过模态叠加法求得。孙文静等[18]通过留数法表达了轨道的格林函数，在频域内分析了不同轨道模型和车速对轨道系统随机振动的影响。SHENG等[19]将格林函数法的应用范围拓展至时域，提出了钢轨的时域移动格林函数。从广义上来说，格林函数法是用于求解“源−场”关系问题的一种行之有效的方法，将“源”分解成若干“点源”，对“点源”产生的场即格林函数进行叠加，从而确定“源”和“场”的关系。尽管推导轨道格林函数的方法各异[20−22]，但其往往决定了格林函数方法的效率。

本文作者兼顾计算精度与速度，基于轨道格林函数研究受离散支承的有砟轨道的垂向振动响应特性，通过傅里叶变换将频域和时域分析相关联，得到轨道的频域和时域格林函数。轨道模型中将钢轨视为无限长Timoshenko 梁，以梁格林函数来推导轨道系统的振动响应，从而避免了采用模态叠加法时截断频率的限制。该方法本质上与波传播法一致，区别在于求解过程中无需将空间响应预设成指数函数的形式，可直接求解运动方程，而不是将载荷以类似边界条件的形式代入。将通过梁格林函数法求得的钢轨频域响应和时域响应分别与2.5D 有限元法和有限元法的计算值进行对比，以验证该方法的可靠性。此外，在常用的传统频域模型中，车轮相对于轨道静止，无法考虑钢轨在移动载荷作用下的多普勒效应，利用格林函数法则可克服这一不足。在此基础上，本文作者研究不同道砟模型对轨道振动响应的影响以及载荷移动速度对钢轨多普勒效应的影响。

1 计算模型

1.1 轨道力学模型

轨道的力学模型如图1所示。钢轨视为无限长Timoshenko 梁，受周期性离散支撑。钢轨的相关参数包括单位长度质量m、弹性模量E、剪切模量G、密度ρ、横截面面积A、截面积惯性矩I和剪切系数κ、从钢轨底部到横截面中性层的距离h。位移与钢轨位置x和时间t有关，包括纵向位移u(x，t)、垂向位移w(x，t)和截面转动角θ(x，t)。Q为作用在钢轨上的载荷。

图1 轨道力学模型Fig.1 Mechanical model of track

将半轨枕视为刚体，其质量和惯性矩分别为Ms和Is。轨枕的位移变量包括横向位移xi(t)、垂向位移zi(t)和转动角αi(t)。模型中共包含N个轨枕，第i个轨枕的位置为li。从轨枕中性层到轨脚和轨枕底部的距离分别为h1和h2；d为相邻2 个轨枕之间的距离。

将扣件和道砟部分视为弹性层，在其起作用的方向上均可等效成弹簧和阻尼器的并联装置（图中仅显示垂向装置）。刚度参数包括kpx，kpz，kpα，kbx和kbz，阻尼参数包括cpx，cpz，cpα，cbx和cbz。刚度和阻尼均为常数，只与扣件和道砟的本身性质相关。

1.2 轨道格林函数

根据轨道力学模型可以得到钢轨和轨枕的运动微分方程组：

式中：δ为狄里克雷函数；Q=δ(x-ξ)e为载荷，e=[0 10]T；qr=[u(x,t)w(x,t)θ(x,t)]T和qri=[u(li,t)w(li,t)θ(li,t)]T为钢轨的位移列向量；为轨枕的位移列向量；Sx,t，Bt，Ct，Dt和Et为3 阶矩阵微分算子，可以根据轨道的振动微分方程整理得到。

对式(1)和式(2)关于t进行傅里叶变换，分别得到式(3)和式(4)：

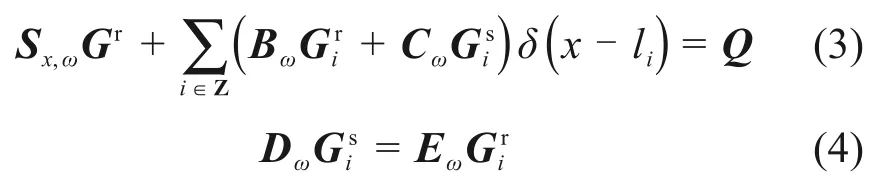
由式(4)得

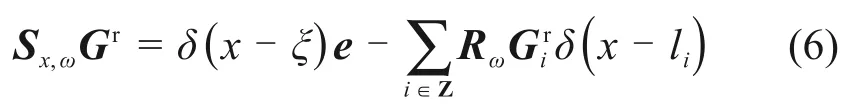
由于钢轨弯曲和纵向位移耦合，可引入矩阵Tx将Sx,ω对角化为

式中：S1和S2为对角矩阵中的元素。

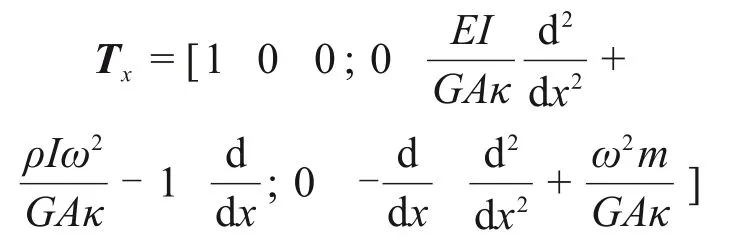
此时，可引入格林函数矩阵

其需满足：

式中：ED为单位矩阵，由式(9)可得

先考虑式(10)右侧为δ(x)的情况，对式(10)进行傅里叶变换后易求解得：

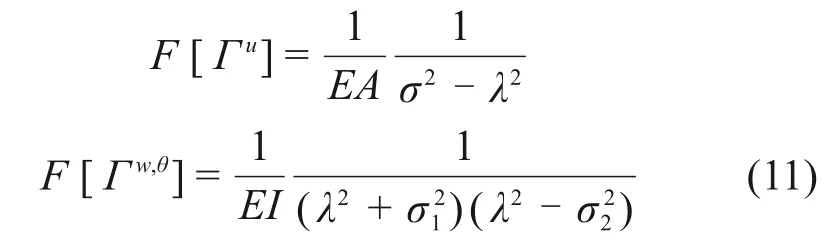
式中：F[.]表示傅里叶变换；σ，σ1和σ2为特征值。将式(11)进行傅里叶逆变换，并用(x−x′)替换x后，即可得无限长杆和Timoshenko梁的格林函数：

于是，式(6)可以写成如下形式：

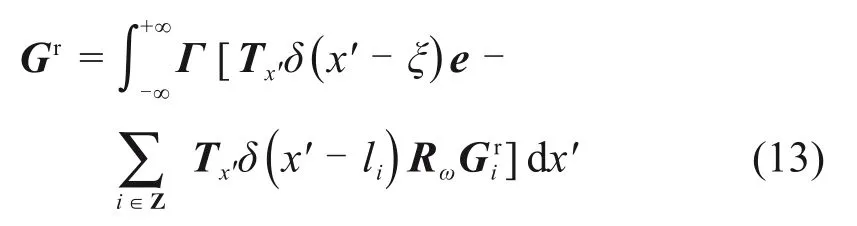
当x=lk时，k为正整数，令Grk=Gr(lk,ξ,ω)及Qk=Γ*(lk,ξ,ω)e，则有

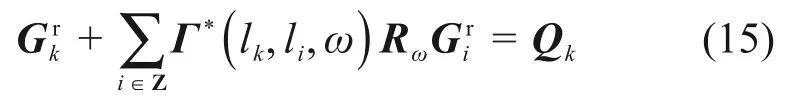
由式(15)可以解出所有轨枕处钢轨的Grk，将其代入式(14)得到任意位置处钢轨的频域格林函数Gr。对Gr进行傅里叶逆变换，有

式中：gr为钢轨的时域格林函数。

2 格林函数验证

轨道格林函数是轨道的固有属性，同种轨道结构对应相同的轨道格林函数。轨道的相关参数如表1所示。数值模拟时轨道模型长度相当于40个轨枕间的跨度。

表1 轨道结构参数Table 1 Structural parameters of track

图2所示为钢轨在激励点处的频域响应，为验证该结果的有效性，图中同时给出了利用2.5D 有限元法计算所得的频响结果。

由图2可见：钢轨的低频响应在90 Hz 和510 Hz 处存在峰值，整个轨道可以视为1 个具有2层弹性层的振动系统，轨枕跨中钢轨的位移导纳比轨枕上方钢轨上的位移导纳略高。在中高频区，轨枕跨中钢轨约在1 070 Hz 出现第一个pinnedpinned 共振，而轨枕上方钢轨由于受到弹性支承，在1 120 Hz 左右出现了反向pinned-pinned 共振；第二个pinned-pinned 共振峰值对应的频率约为2 870 Hz，2 个激励点处钢轨的位移导纳均达到最小；第三个pinned-pinned 共振峰值对应频率约为4 670 Hz，轨枕跨中钢轨的位移导纳最大，轨枕上方钢轨的位移导纳最小。

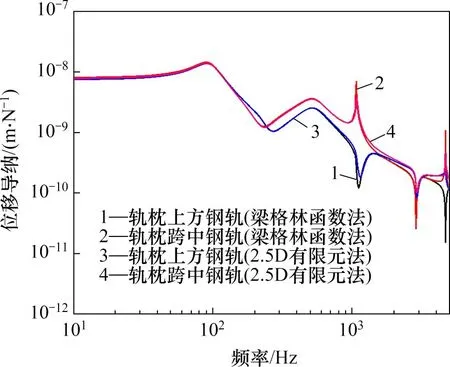
图2 不同方法计算的钢轨频域响应Fig.2 Frequency-domain response of rail with different methods

对比分别利用梁格林函数法与2.5D有限元法计算得到的钢轨频域响应结果可见：两者在2 000 Hz以下的频域范围内能保持较好的一致性；在更高的频域内，由于钢轨会发生截面变形，不再表现出梁的振动行为，2种方法所得计算结果将会出现明显差异。这是将钢轨当成梁来处理所不可避免的，但总体来说，在梁模型所考虑的频率范围内，该方法有效。

利用时域格林函数可以对钢轨的垂向冲击响应进行时域分析，图3所示为钢轨的时域响应，即钢轨在脉冲激励下的响应。图中同时给出了利用有限元软件ANSYS对轨道进行瞬态分析得到的时域响应结果，用以验证本文方法的准确性。

图3 不同方法计算的钢轨时域响应Fig.3 Time-domain response of rail with different methods

由图3可见：对于轨枕跨中钢轨，响应的最大值约为6.54 μm/(N·s)，响应主要由90 Hz和1 070 Hz对应的振荡混合决定，正好对应其频响中的共振和一阶pinned-pinned 共振。对于轨枕上方钢轨，由于受到支承作用，灵敏度相对于跨中钢轨略低，其时域响应几乎是1条平滑的曲线，冲击响应的最大值约为4.04 μm/(N·s)，主要由频域中的共振频率所对应的振荡主导。

通过与有限元法的瞬态分析计算结果对比可知，梁格林函数法计算得到的轨枕上方的时域响应与有限元结果基本一致，而跨中钢轨响应曲线的波动幅度比有限元结果的大，这是由于相较于有限元模型，梁模型是对实际轨道结构的简化描述，其在当前所用的轨道结构参数条件下计算所得的一阶pinned-pinned 共振略大所导致。总体而言，梁格林函数法与有限元法计算所得时域响应的结果相符。但有限元法由于受到网格数量等因素影响，在本文中进行一次瞬态分析需要约1 h，而通过梁格林函数计算轨道时域响应可以在几秒内完成。可见，在满足一定精度要求的前提下，采用梁格林函数的计算效率要远比有限元法的计算效率高。

3 轨道振动响应特性

通过与2.5D 有限元法和有限元法的计算结果对比，说明了梁格林函数在频域和时域分析中的可靠性，以及在计算上的高效性。轨道的振动响应受到诸多因素影响，下面应用该方法对有砟轨道的振动响应进行进一步研究。

3.1 道砟质量影响

对于有砟轨道，道砟部分的质量对轨道响应的影响不可忽视，前述轨道模型中将道砟部分等效为轨枕与地基之间的弹性层，而忽略了道砟部分的质量。为了能显著体现出道砟的吸振效果，可以在原模型的基础上，用道砟质量块模型替换简化的道砟弹性层模型，如图4所示。

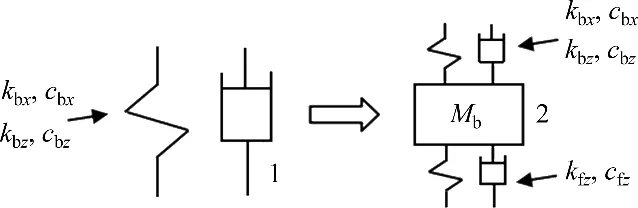
图4 道砟模型Fig.4 Mechanical model of ballast

在道砟质量块模型中，道砟等效振动质量Mb为531 kg，道砟与地基之间的刚度kfz为78 MN/m，阻尼cfz为31 kN·s/m。图5所示为利用2种道砟模型计算得到的轨道在激励点处的频域响应。

由图5可见：利用2种道砟模型计算得到的轨道频域响应结果的区别主要在300 Hz 以下的低频区域，道砟质量块模型中的钢轨位移导纳更高，且共振频率也更低；在300 Hz以上的中高频范围，2种模型计算所得的频响结果基本相同。此外，考虑道砟质量后，在80 Hz左右的道砟频响比钢轨频响大，此时道砟表现出明显的吸振作用，而轨枕的吸振作用则发生在更高的频率，约为210 Hz。实际上，把道砟处理成质量块会增加轨下支撑部分的柔度，这对钢轨的高频响应影响甚微。

图5 不同模型计算的轨道频域响应Fig.5 Frequency-domain responses of track with different models

为了更进一步研究轨道的垂向冲击响应，可以利用时域格林函数进行时域分析。图6所示为利用2种道砟模型计算所得的钢轨部分的冲击响应。

由图6可见：与道砟弹性层模型相比，道砟质量块模型中钢轨的冲击响应最大值没有明显区别，其主要差异在于响应的衰减速度减缓，这是主导其衰减的振荡所对应的频率减小所致，该频率即对应钢轨频响中的共振频率。

图6 不同模型计算的钢轨时域响应Fig.6 Time-domain responses of rail with different models

3.2 多普勒效应

轨道格林函数反映了轨道在静态力作用下的振动响应，其只与轨道本身的结构属性相关。在已知轨道格林函数的基础上，可进一步研究轨道在动态力作用下的响应。图7所示为钢轨在速度为60 m/s的移动单位载荷作用下的频域响应。

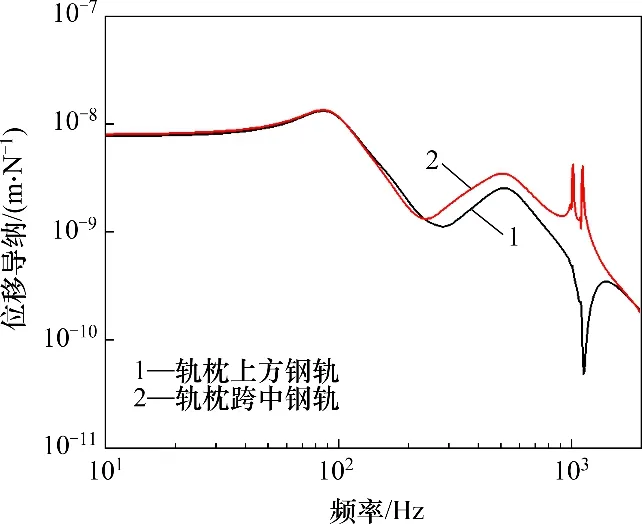
图7 钢轨位移导纳Fig.7 Receptance of rail

由图7可见：当轨道受到移动载荷激励时，轨枕跨中钢轨在pinned-pinned 共振频率附近会出现多普勒效应，原本在静载作用下的单个pinnedpinned峰值会发生分叉现象，形成2个共振峰，且峰值会减小，而对于轨枕上方钢轨则没有类似的现象。实际上，多普勒效应是载荷与轨道发生相对移动的必然结果，利用格林函数方法可以很好地反映这一现象。多普勒效应与速度相关。图8所示为在不同速度的移动载荷作用下，轨枕跨中钢轨在pinned-pinned共振频率附近的位移导纳。

由图8可见：速度对轨枕跨中钢轨在高频范围内的多普勒效应有显著影响。随载荷移动速度不断增大，在pinned-pinned 共振频域内，峰值逐渐减小，且峰值所对应的频率相差也越来越大，多普勒效应越明显，这也可以间接反映移动载荷作用下轨道时域响应的复杂性。事实上，pinnedpinned共振与钢轨波磨的发展关系较大，因此，研究移动载荷作用下钢轨在pinned-pinned 共振区域的多普勒效应对后续研究钢轨波磨的发展很有意义。

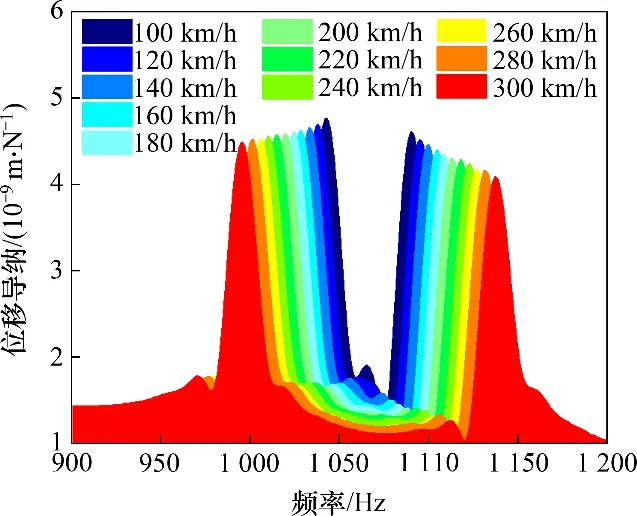
图8 跨中钢轨位移导纳Fig.8 Receptance of rail at mid span

4 结论

1)应用梁格林函数法与2.5D 有限元方法计算所得的频响结果在2 000 Hz以下的频域范围内基本相同，与有限元方法计算所得的时域响应亦基本保持一致，表明该方法在轨道振动响应计算中具有较高的可靠性，且该方法的计算效率远比有限元方法的计算效率高。

2)考虑道砟质量后，在频域内会增大钢轨的低频响应，并降低其共振频率，但不影响钢轨在中高频范围内的响应；在时域内，轨道冲击响应的衰减速度会减缓。

3)移动载荷的作用会导致轨枕跨中钢轨在一阶pinned-pinned 共振频率附近产生多普勒效应，原本在静载作用下的单个pinned-pinned 共振峰会分叉形成2个峰，且随载荷移动速度增大，分叉越明显，峰值越小。

4)轨道格林函数是轨道系统的固有属性，后续借助赫兹弹性接触理论可进一步计算轮轨接触力。轨道格林函数是轨道在轮轨相互作用中始终保持不变的位移相关函数，应用格林函数方法可避免由于激励变化导致的位移相关量的重复求解。