均匀直流电场作用下贴壁气泡变形特性
王太,陈烁,李典,刘清元,谢英柏,刘春涛
(华北电力大学能源动力与机械工程学院,河北保定,071003)
电场强化沸腾换热技术具有设备简单、装置灵巧、功耗低、热流与温度易于控制等优点[1],在动力工程、核能工程、化学工程、航空航天等领域具有广阔的应用前景。该技术通过施加高压电场,在汽液界面产生电场力,从而控制汽泡的生成、脱离以及变形、融合、破碎等拓扑结构的变化。可见,深入研究外加电场作用下气泡的动力学行为,有助于认识电场强化沸腾换热的机理。
鉴于此,国内外众多学者对电场作用下气泡动力学行为进行了研究。PENG 等[2]采用实验方法研究了均匀电场作用下气泡的生成与脱离过程,分析了电场强度、出气孔孔径的影响,发现气泡沿电场方向伸长,且电场强度越大,气泡变形越明显。DI 等[3−5]证明了电场具有操控气液界面拓扑变化的能力。LIU 等[6]在出气孔右上方安置了1 个高压球形电极,构建了非均匀电场,并研究了气泡的生成、脱离与上升过程。WANG等[7]将竖直金属圆柱与金属平板平行放置构建了非均匀电场,并研究了气泡在非均匀电场中的上升过程;JALAAL 等[8]在出气口左侧安置了1 个高压平板电极(竖直方向),观察了在非均匀电场作用下气泡远离高电场强度区域。高明等[9]利用针状电极与加热平面电极构建了非均匀电场,观测了外加电场对单个沸腾汽泡动力学特性的影响。王军锋等[10]利用针状电极与环状电极构建了非均匀电场,观测了非均匀电场中气泡的生成与分散特性。HIGUERA等[11]采用数值模拟的方法研究了均匀电场作用下单个气泡的生长与脱离过程;陈帅等[12]采用数值模拟研究了交流电场作用下附着在下壁面上气泡的变形与脱离过程。MÄHLMANN等[13−18]模拟了均匀电场中气泡的上升过程,发现气泡沿电场方向伸长,从而影响上升速度。SUNDER 等[19]采用CLSVOF方法对非均匀电场作用下浸没孔中气泡的生长与脱离过程进行了数值模拟研究,发现改变非均匀电场的分布可控制生成气泡的直径,提升气泡的脱离速度。这些研究展示了外加电场对气泡动力学行为的作用规律,为揭示电场强化沸腾换热的机理提供了理论参考。
现有研究多集中于电场作用下气泡的生成、脱离与上升等行为,但在水平通道内,沸腾换热产生的汽泡会上升并与上壁面接触,而电场作用下贴壁气泡的动力学行为研究仍报道较少。因此,本文作者将电场力模型与基于轴对称坐标系的气液两相流数值算法相耦合,数值模拟研究外加均匀直流电场作用下贴壁气泡的变形特性,重点分析电场力、浮升力、表面张力、毛细力的影响机理。
1 数值模型
1.1 控制方程
对于不可压缩气液两相流动,施加电场后,气液界面上存在电场力,此时连续性方程与动量方程可描述为:
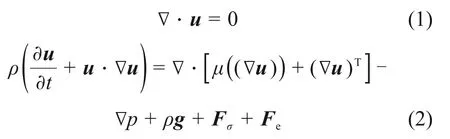
式中:u,ρ,t,μ,p和g分别为速度矢量、流体密度、时间、黏度、压力和重力加速度;Fσ为表面张力;Fe为电场力。采用基于同位网格的IDEAL算法[20]求解流场,采用ADI算法[21]求解离散方程组。
1.2 界面追踪方法
VOF 方法与Level Set 方法是模拟气液两相流动的常用算法,但是这2 种方法的优缺点也较明显。VOF 方法能够确保各相的质量守恒,但是很难精确计算表面张力;Level Set方法能够精确计算表面张力,但是很难保证各相的质量守恒。为了解决这个问题,SUN 等[22]提出了VOSET 界面追踪方法,该方法采用VOF 方法捕捉相界面,采用Level Set 函数计算表面张力和流体物性,结合了VOF方法与Level Set方法的优点。
VOF方法的流体体积函数输运方程为
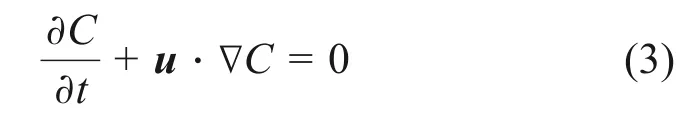
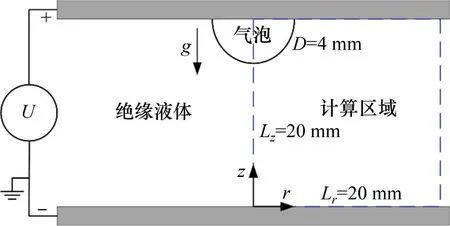
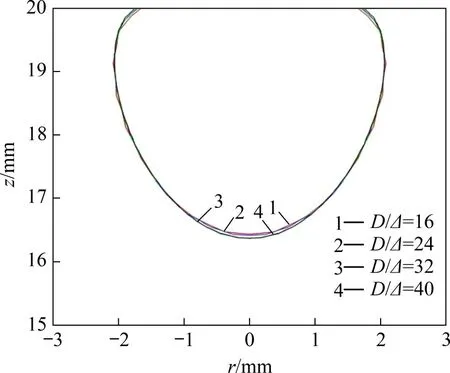
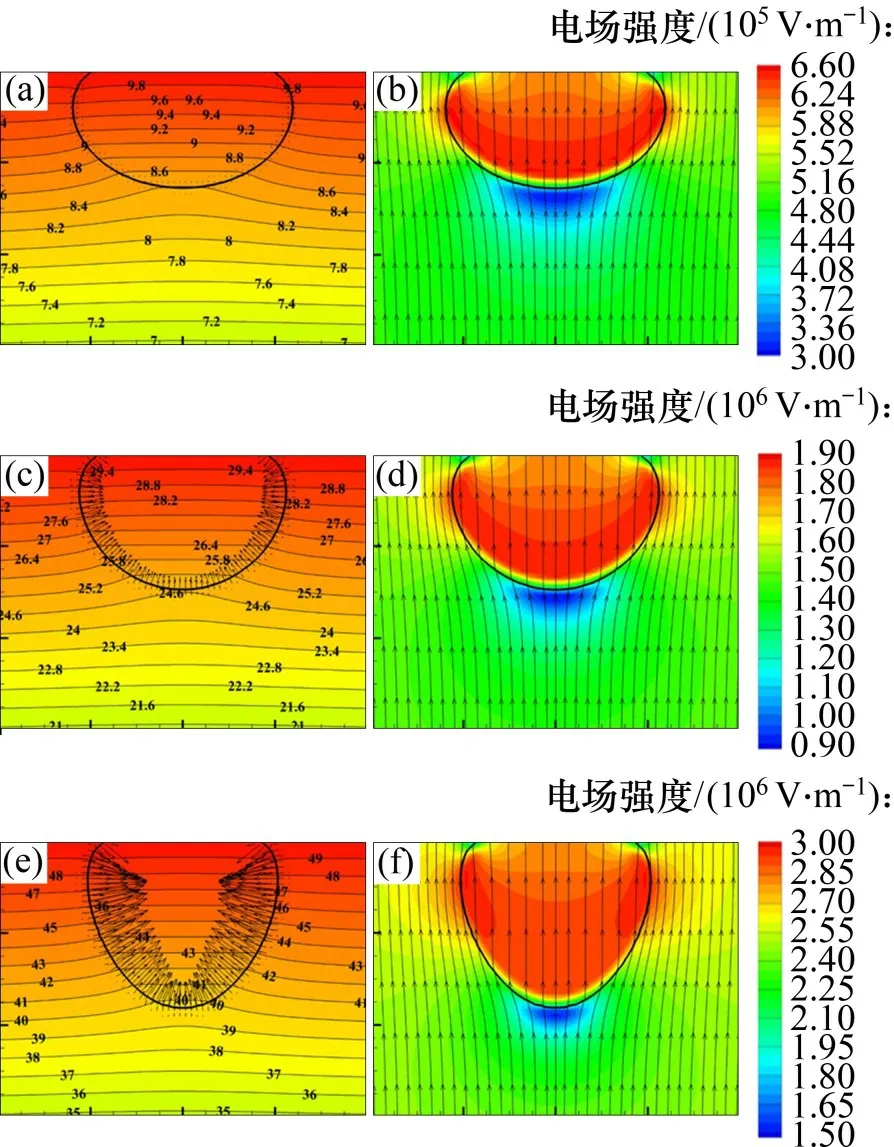
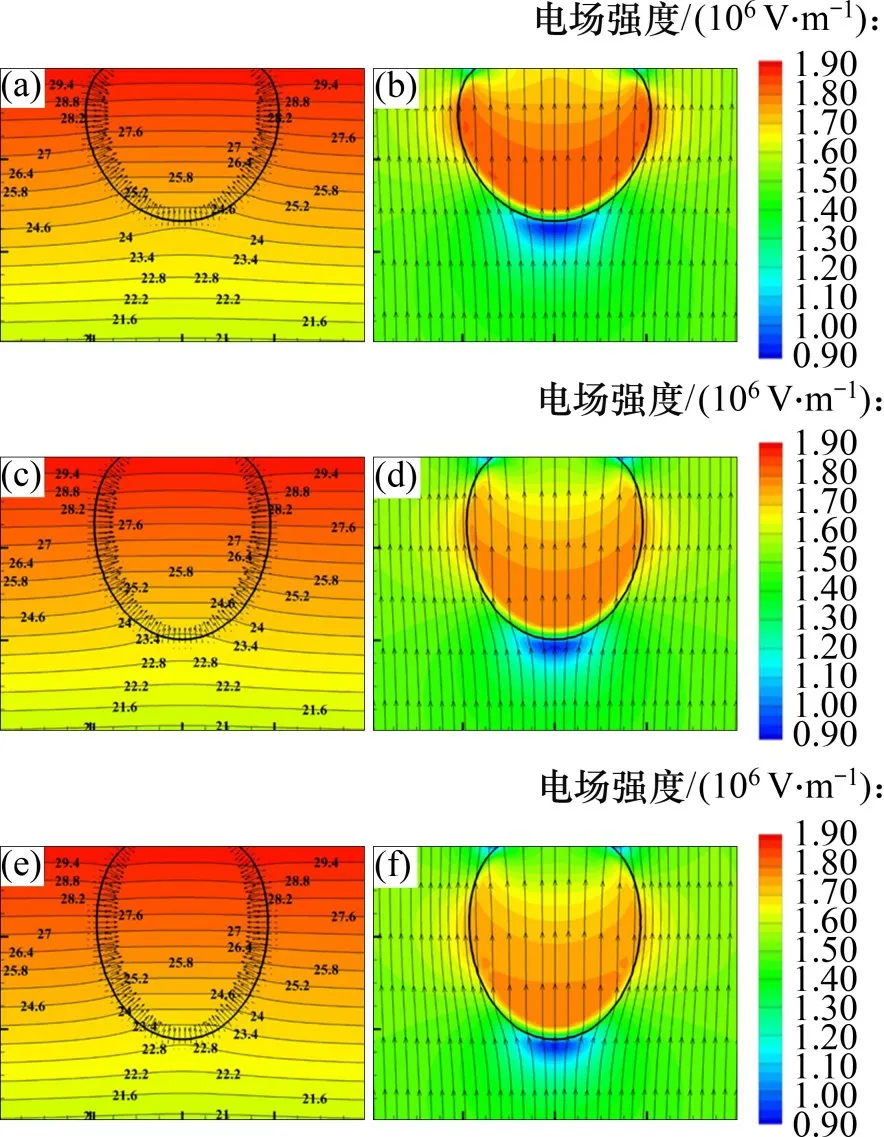
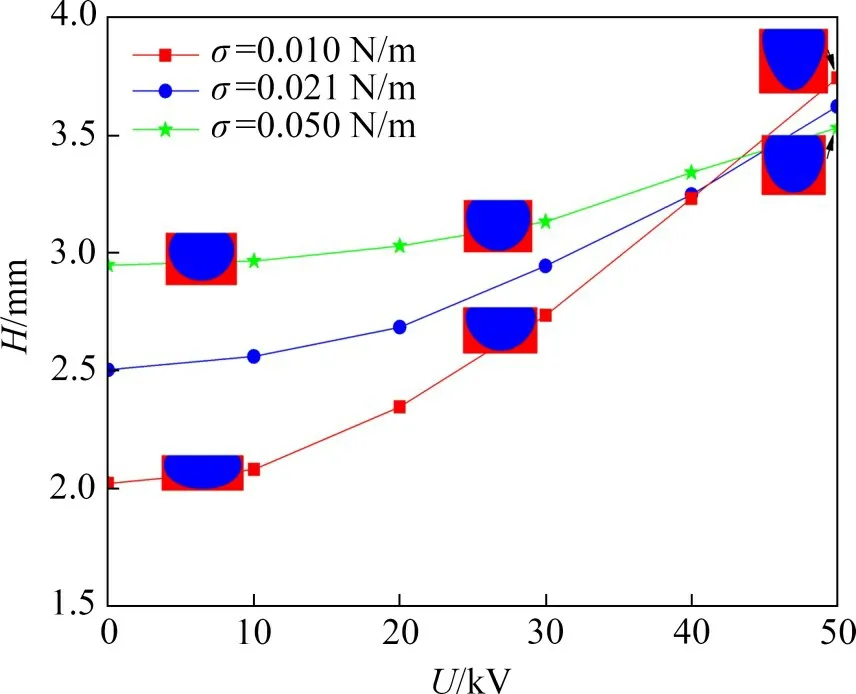
式中:C为流体体积函数,表示目标流体占网格单元的体积分数。C=0表示网格内全为液体,C=1表示网格内全为气体,0 采用几何方法[22]计算相界面周围网格中心P点到相界面的最短距离d,根据网格中心的位置,确定Level Set函数ϕ,计算式如下: 获得Level Set函数ϕ后,采用CSF界面张力模型[25]计算表面张力Fσ 式中:σ为表面张力系数;κ为界面曲率,表达式为 其中,δ(ϕ)为Dirac Delta函数,表达式为[26] 式中:γ为相界面周围的光滑宽度,等于1.5Δ,Δ为网格宽度。 利用Heaviside 函数H(ϕ)[26],通过插值平均方法计算流体的密度ρ、黏度μ及相对介电常数ε。 式中:下标l和g分别表示液体与气体。 H(ϕ)的表达式为 在电流体动力学中,磁效应非常微弱,可忽略不计,因此,电场强度E是无旋的,即∇×E=0。对于理想介质材料,电场强度E满足以下方程: 式中:ε0为真空介电常数。 引入标量电势ψ,定义电场强度E=-∇ψ,代入式(12),可得 采用中心差分格式离散上述方程,并采用ADI算法求解离散方程组,获得电势ψ的分布后,计算电场强度E的分布,从而计算电场力Fe。将电场力代入动量方程,求解速度场,从而获得下一时刻的气液界面分布;随后可再计算电场力的分布,再次代入动量方程,从而实现电场与流场的耦合。 图1所示为外加电场作用下贴壁气泡的物理模型示意图。由图1可见:2 块极板平行放置,上极板与高压电源正极相连,下极板与高压电源负极相连并接地;初始时刻,气泡置于上极板下方,连续相为绝缘液体;改变施加于极板之间的电压U,气泡的形状将随之发生变化。由于气泡的变形具有轴对称特性,因此,取1 rad 区域作为计算区域,Lr=Lz=20 mm(Lr为径向长度,Lz为轴向长度),气泡的当量直径D=4 mm,气泡的高度为H。求解流动方程所采用的边界条件为:1)左边界(r=0)为轴对称边界;2)右边界(r=Lr)为滑移边界;3)下边界(z=0)与上边界(z=Lz)为无滑移边界条件,气液固三相接触角为θ=20°。 图1 物理模型与计算区域Fig.1 Physical model and computational domain 求解电势方程的边界条件为: 式中:ψ0为直流电场中上壁面的电势。 选择合适的网格精度,既可以获得精确的数值模拟结果,又可以控制计算资源的消耗,因此,有必要开展网格无关性验证。选取80×80,120×120,160×160和200×200这4种网格系统(D/Δ分别为16,24,32和40),模拟U=50 kV时二甲基硅油(型号为1000cs)中气泡的变形,空气和二甲基硅油的物性参数见表1。图2所示为不同网格精度下气泡形状的对比结果。从图2可以看出:随网格精度提高,气泡高度H略有增加,但D/Δ=32与D/Δ=40网格的模拟结果差异极小,因此,采用D/Δ=32 网格开展后续数值模拟研究。 表1 不同流体的物性参数Table 1 Physical parameters for different fluids 图2 不同网格分辨率时气泡的形状Fig.2 Bubble shapes for different grid resolutions 为了验证数值模型的准确性,本文设计与搭建了用于研究均匀直流电场作用下贴壁气泡变形特性的可视化实验系统。如图3所示,实验系统由高压直流电源(0~50 kV)、摄像机、冷光源、电极板(100 mm×100 mm)等组成,2极板间距为20 mm,实验工质为空气与二甲基硅油;标尺置于上、下极板之间,将拍摄的图片放大,读取每厘米标尺上包含的像素点个数,可获得每个像素点代表的尺寸,读取气泡沿竖直方向包含的像素点个数,乘以像素点的尺寸,即可获得气泡高度。 图3 实验系统示意图Fig.3 Schematic diagram of experimental system 通过实验观测了D=3.8 mm与D=4.91 mm的气泡在不同电场强度时的形变,同时对实验工况进行了数值模拟。图4所示为不同直径气泡在不同电场强度时形变的数值模拟结果与实验结果的对比,从图4可以看出:不同直径气泡在不同电场强度时形变的数值模拟结果与实验结果吻合良好,证明本文数值模型可有效地模拟外加电场作用下气泡的动力学行为。 图4 不同直径气泡在不同电场强度时形变的数值模拟结果与实验结果的对比Fig.4 Comparison between numerical results and experimental results for bubble with different diameters under effect of different electric field strengths 直流电场中,上下极板的电势不随时间变化,施加电场之后,气泡经过短暂时间,会达到静态平衡,此时气泡受到电场力、浮升力、表面张力、毛细力的作用。 由图4可知,施加电场后,气泡沿竖直方向伸长,且电压U越大,气泡变形越明显。为了揭示电场作用下气泡变形的机理,图5所示为不同电场作用下二甲基硅油中气泡(D=4 mm)的形状及周围电场强度(|E|)、电势、电场线、电场力的分布。对单相均质流体施加均匀电场,电势由高压极板到低压极板线性减小,电场强度为定值。从图5可以看出:添加气泡之后,气液界面周围的电势发生扭曲,且气泡顶端附近电势扭曲程度最大,造成气泡内部电势等值线密度比气泡外部密度大;电场线同样在气液界面周围发生扭曲,且背离气泡方向弯曲。气泡内部的电场强度远比气泡外部的电场强度大,气泡左右两侧界面处于较强电场强度区域,而气泡顶端界面处于较弱电场强度区域,造成气泡顶端的电场力比左右两侧的小。同时,由于电场力指向气泡内部,因此,在挤压作用下气泡沿竖直方向伸长,且随电压U增大,电场强度增大,气液界面上的电场力明显增大,克服表面张力与浮升力的作用,导致气泡变形更明显。 图5 不同电场作用下二甲基硅油中气泡(D=4 mm)的形状及周围电场强度、电势、电场线及电场力的分布Fig.5 Distributions of electric field intensity,electric potential,electric field line and electric field force around bubble with D=4 mm in dimethyl silicone oil under effect of different electric fields 由电势和电场力的求解方程可知,引起电势与电场扭曲的根源在于气液两相的介电常数存在差异,同时也是造成相界面上存在电场力的主要原因。为了分析流体介电常数的影响,在数值模拟过程中,改变液体的介电常数,其他物性与二甲基硅油的物性相同。图6所示为不同介电常数液体中气泡形状与高度随电压U的变化。由图6可知:当无外加电场时,不同介电常数对气泡的高度无影响。施加电场后,气泡高度随电场强度增大而增大,且介电常数越大的液体中气泡高度的增加幅度越大。同时,气泡形状也发生了明显变化,气泡端部越来越尖,如U=50 kV 工况,随液体介电常数增大,气泡由短弹头状演变为尖刺状。 1)“目标—发展”开发模式。人的发展是三维目标的整合,能力发展是核心,知识是结果的基础,情感态度价值观养成是灵魂,过程与方法是关键。该模式是较低层次,是最基本的微课(程)开发模式,但具有普遍性,适用于各层次学者选择,具有较强的可接受性、可操作性和指向性。微课(程)“目标—发展”开发模式流程简图如图1所示。 图6 不同介电常数液体中气泡形状与高度H随电压U的变化Fig.6 Variations of bubble shape and height H with voltage U in liquids with different dielectric coefficients 为了了解介电常数的影响机理,图7所示为U=30 kV时,介点常数ε分别为5,10和30的液体中气泡周围电场强度(|E|)、电势、电场线、电场力的分布,图7(a),图7(c)和图7(e)中电场力矢量的单位长度代表的值分别为图5(c)的2.5倍、2.5倍与10倍。由图7可知:介电常数的增大使气液界面附近电场线的扭曲更加严重,气泡内部电场线的密度越来越低;介电常数对电场力的分布无明显影响,但随介电常数增大,电场力明显增大,挤压作用更加明显,使气泡更加瘦长。通过电场力的计算公式可知,气液两相的介电常数差异越大,气液界面周围介电常数的梯度(∇ε)越大,因此,电场力越大。 图7 U=30 kV,介点常数ε为5,10和30时液体中气泡周围电场强度、电势、电场线、电场力的分布Fig.7 Distributions of electric field intensity,electric potential,electric field line and electric field force around bubble in liquids with ε=5,10,30 and U=30 kV 气泡上表面受到液体向下的压力,而下表面受到液体向上的压力,两者之差形成浮升力。在浮升力作用下气泡向上运动,并与上壁面接触,随后在气泡下表面受到的液体向上的压力作用下,气泡被向上挤压。浮升力不同,气泡受到的挤压程度不同,必然影响电场中气泡的变形。影响浮升力的2 个重要因素为重力加速度与气液密度差,两者与浮升力呈线性关系,影响规律相近。 图8所示为不同重力环境下二甲基硅油中气泡形状与高度H随电压U的变化。由图8可知:在常重力环境(g=g0=9.81 m/s2)中,当浮升力作用较强,电场强度较小时,电场力较小,不足以克服浮升力的作用,气泡呈扁帽状;随电场强度增大,电场力作用增强,气泡逐渐演化为短弹头状,气泡高度随之增大,且增大的幅度也逐渐增大,这主要是因为电场力与电场强度呈平方关系,而非线性关系。随重力加速度减小,浮升力作用减弱,当电场强度较小时,表面张力与毛细力占主导作用,气泡由扁帽状逐渐演化为削顶的球状;当电场强度较大时,电场力作用更加明显,气泡由短弹头状演化为长弹头状,且气泡高度也明显增大。 图8 不同重力环境中气泡形状与高度H随电压U的变化Fig.8 Variations of bubble shape and height H with voltage U in different gravity environments 图9所示为U=30 kV 时g=0.50g0,0.10g0,0.01g0环境中气泡周围电场强度(|E|)、电势、电场线、电场力的分布。从图9可以看出:重力加速度的变化对电势与电场线的扭曲无明显影响;随重力加速度减小,气泡内部的电场强度略有减小,这是因为气泡沿竖直方向伸长,导致气泡左右两侧的界面曲率减小。由于气泡周围电场强度减小的幅度很小,因此,电场力的差异较小。 图9 U=30 kV,g为0.50g0,0.10g0和0.01g0环境中气泡周围电场强度、电势、电场线、电场力的分布Fig.9 Distributions of electric field intensity,electric potential,electric field line and electric field force around bubble in liquids with g=0.50g,0.10g,0.01g and U=30 kV 表面张力具有维持气泡形状的能力,对气泡的形变具有重要影响。为了研究表面张力的影响,在数值模拟过程中,改变表面张力系数,液体的其他物性与二甲基硅油的物性相同。 图10所示为σ=0.010 N/m 和0.050 N/m 时气泡形状与高度H随电压U的变化。由图10可知:当无外加电场时,表面张力系数越小,维持气泡形状的能力越弱,气泡高度越小,呈现扁帽状;而当表面张力系数较大时,维持气泡形状的能力较强,气泡高度较大,呈现球帽状。施加电场后,随电场强度增大,气泡高度逐渐增大,且表面张力系数越小,气泡高度增加的幅度越大。当U=0 kV时,σ=0.010 N/m工况对应的气泡高度远比σ=0.050 N/m 工况的高度小;随U增大,两者之间的差距减小,当U=50 kV 时,σ=0.010 N/m 工况对应的气泡高度比σ=0.050 N/m工况对应的高度大。 图10 σ为0.010和0.050时气泡形状与高度H随电压U的变化Fig.10 Variations of bubble shape and height H with voltage U for σ=0.010 and σ=0.050 电场力与表面张力均作用于气液界面,且指向气泡内部。当表面张力较大时,电场力在界面力中的占比较小,因此,电场力增大对气泡形变影响较小;而当表面张力较小时,电场力在界面力中的占比明显增大,随电场力增大,气泡高度明显增大。 图11所示为在不同接触角时,二甲基硅油中气泡形状与高度H随电压U的变化。由图11可知:当无外加电场时,随接触角增大,气泡高度显著减小,气泡由球帽状逐渐演变为圆饼状,气泡与固体壁面的接触面积明显增大。这是因为当接触角小于90°时,毛细力指向气泡内部,拉动气液固接触线向内收缩,且接触角越小,毛细力作用越明显,接触线向内收缩越明显,使气泡高度较高;当接触角大于90°时,毛细力指向气泡外部,使接触线外延,且接触角越大,现象越明显,气泡呈圆饼状,高度减小。施加电场后,在电场力的挤压作用下,气泡高度随电场强度增大而增大,且接触角越小,气泡高度增加的幅度越大。 图11 不同润湿壁面上气泡形状与高度H随电压U的变化Fig.11 Variations of bubble shape and height H with voltage U for wall with different wettabilities 从图11可以看出:接触角越大,气液界面的曲率越小,由于表面张力系数相同,因此,相界面上的表面张力越小。当表面张力较小时,电场力在界面力中的占比较大,对气泡变形影响更明显,因此,接触角越大,气泡高度随电场强度增加而增大的幅度越大。 1)电势与电场在气液界面附近发生扭曲,且液体介电常数越大,扭曲程度越大;电场力指向气泡内部,且非均匀分布,气泡在电场力的挤压作用下沿电场方向伸长。 2)电场强度与流体介电常数是电场力的重要因素,电场强度与液体介电常数越大,电场力越大,气泡变形越明显。 3)浮升力越小,液体对气泡的作用力减弱,电场力的作用增强,使气泡高度增大;表面张力具有维持气泡形状的能力,表面张力系数越小,气泡高度随电场强度增加而增大的幅度越大;接触角越大,气泡与固体壁面的接触面积越大,且气泡高度随电场强度增加而增大的幅度越大。


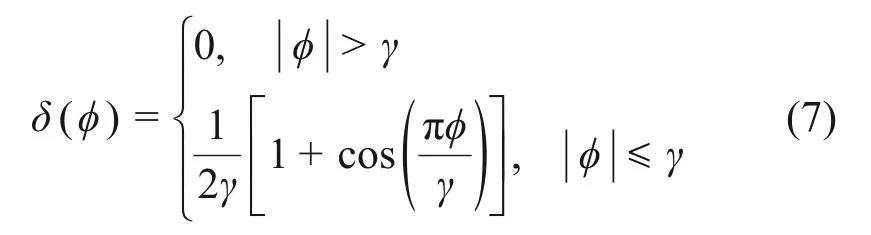
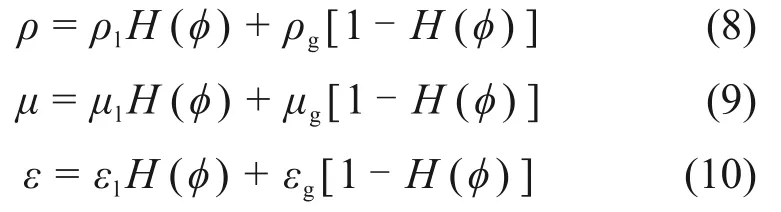
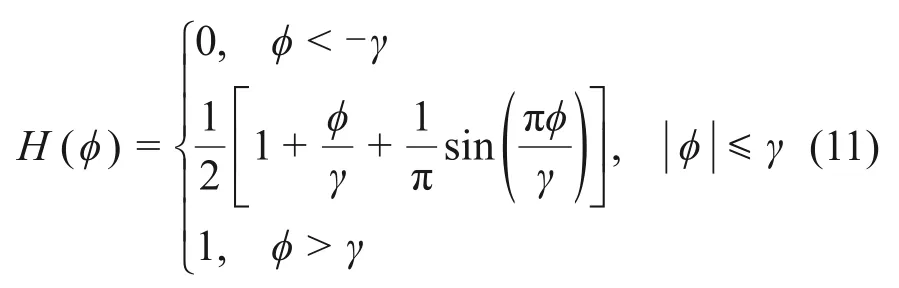
1.3 电场力模型



1.4 计算区域与边界条件

2 模型验证
2.1 网格无关性验证

2.2 实验验证


3 结果与讨论
3.1 电场强度的影响
3.2 介电常数的影响


3.3 浮升力的影响

3.4 表面张力的影响
3.5 毛细力的影响

4 结论

