基于空心球滑移条件下的双梯度钻井井筒温压场的研究

张锐尧，李军, ，柳贡慧, ，杨宏伟，王江帅，高热雨

1 中国石油大学(北京)石油工程学院，北京 102249

2 中国石油大学(克拉玛依)石油工程学院，克拉玛依 840000

3 北京工业大学机械工程学院，北京 100124

0 引言

2019年中国原油进口量突破5亿t，对外依存度达到70%[1-3]。并且随着我国浅部地层优质油气资源的持续开采，未来我国勘探开发实现增产的主战场会逐渐瞄准了“难动用” 的油气资源， 特别是海洋油气资源[4-5]。但是深水钻井过程中，由于存在复杂的温度场环境以及孔隙压力高、破裂压力低所形成的窄压力窗口[6-8]，所以极易引起溢流、气侵或漏失等井下复杂情况。为了应对该技术难题，国内外学者先后研究出了精细控压钻井、双梯度钻井等钻井技术[9]。虽然该技术都有现场应用的成功先例，但是前者的控制系统复杂，成本较高；后者技术的实现需要增加海底泵和旁通管线，设备安装复杂，且只能调节海底泥线以上的密度梯度，可调井筒压力范围窄[10-12]。而注空心多梯度钻井可以在海底泥线以下环空形成多个密度梯度，通过分离器将空心球从钻杆内分离进入上部环空。因为空心球密度比钻井液低，所以以分离器为参考点，在上、下环空形成了两个密度梯度，如果多点安装即可以形成多个密度梯度。这样就使得在钻遇窄压力窗口时，井筒压力可调范围广，避免了传统钻井井筒压力分布单一与现有双梯度钻井技术的局限性。但是多梯度钻井过程中因为空心球的密度小于钻井液密度，并且空心球与空心球在运动过程中存在碰撞，从而导致空心球在环空中运动时存在滑移现象。而空心球的滑移会使得上部环空的压力过小，下部环空的压力过大，从而导致上部溢流而下部漏失等复杂情况。所以本文考虑空心球之间的碰撞，建立了球—球曳力模型，基于空心球受力进一步推导了滑移速率数学模型，并基于该模型进行了计算和敏感性分析，且通过室内实验对模型进行了验证。然后在考虑空心球的滑移条件下，建立了双梯度钻井随钻井底压力预测模型，最后结合钻井数据对模型进行了计算和敏感性分析。

1 空心球的滑移速率数学模型

空心球在钻井液中运动时，主要受到钻井液的曳力、重力、浮力以及空心球与空心球之间碰撞产生的曳力。对于空心球在钻井液中的运动过程，现作如下假设：(1)空心球为弹性均质小球，碰撞过程中不考虑破碎的情况；(2)不考虑空心球在分离过程中所产生的波动压力对空心球滑移的影响；

空心球a与空心球b为一个碰撞对，则在一个碰撞控制体单元中包括若干个碰撞对，所以控制体系统中碰撞的总数量是分析空心球相互作用的重要参数之一[13]。本文主要研究空心球的一对一碰撞过程，则根据球-球碰撞的原理即数量守恒方程式(1)，可以得到控制体系统中每个空心球的碰撞体积以及碰撞对的总数量为式(2)和(3)所示：

其中n为空心球的数量；α为空心球的体积分数，%；d为空心球的直径，mm；ρ为空心球的密度，kg/m3；空心球碰撞时的球心距离为dab，mm；Vp为球的碰撞体积，mm3，Np系统碰撞对的数量。

在控制体系统中单位时间内碰撞的数量即碰撞频率为：

根据碰撞前后动量守恒可以得到动量守恒方程以及两球在碰撞前后的相对速度：

假设某时刻空心球的碰撞方向为则与其正交的两个方向分别为故定义单位方向向量从而得到空心球非弹性碰撞的能量损失为：

其中m为空心球的质量，为碰撞前的速度，m/s；为碰撞后的速度 ,为碰撞前的速度差，m/s；e，f，g为碰撞时接触面的法向恢复系数以及切向恢复系数[14-15]，0＜e＜1，若忽略空心球在碰撞时的旋转运动，则法向恢复系数与切向恢复系数相同。

又根据空心球的质量与碰撞前后的速度，可以得到空心球碰撞对的中心速度。

根据上式可以得到式(13)和式(14)，进一步整理可得到式(15)和式(16)：

故空心球a和b在碰撞前后的速度变化为：

其中m0为a、b球的质量和，kg/m3；为碰撞对的中心速度，m/s；M为质量分数,%。

在碰撞过程中能量的损失主要分为非弹性碰撞引起的能量损失以及表面能量损失两个部分，故可以得到碰撞时产生的总的能量损失为：

其中ΔEp为总能量损失，J；ΔEe为非弹性碰撞的能量损失，J；ΔEs为表面能损失，J。

又因为非弹性碰撞损失的能量为：

而球—球在碰撞过程中由附着力引起的表面能量损失可以由无量纲常数λc表示：

故结合表面能量损失以及非弹性碰撞能量损失，并参考式(20)的表达形式可以得到总的能量损失为：

因此在控制体系统中碰撞产生的总的能量传递为：

由于在多梯度钻井过程中所选择的空心球都为等直径、均质小球，若球直径为ds。碰撞时满足dab=ds所以上式可以简化为：

因为空心球粒径小，相对环空中钻井液的流动而言，其加速过程可以忽略不计[16]。如图1所示为空心球在钻井液中的受力情况，以井眼轴线向上方向为正向，以空心球为分析对象，建立如下平衡关系：

图1 空心球受力分析Fig.1 Stress analysis of HGS

其中G为重力，N；FDL为钻井液的曳力，N；FDS为碰撞产生的球-球之间的曳力，N；Ff为钻井液的浮力，N；θ为碰撞方向与井眼方向的夹角，°；VLS为滑移速度，m/s；CD为钻井液对空心球的曳力系数；ρs为空心球的密度，kg/m3。

当颗粒雷诺数Res＜2时，流动状态为层流，CD=24/Res；2 ＜Res＜500时，流动状态为过渡流，CD=18.5（/Res）0.6；500＜Res＜ 2 ×105， 流 动 状 态 为紊流，CD=0.44。当钻井液密度为ρm，黏度为μm，Res=dsVLSρm/μm，得到不同流动状态时的空心球滑移速率如下：

因为空心球与钻井液之间存在密度差所以导致滑移，而滑移过程又会导致空心球与钻井液产生速度差。所以当空心球的滑移速率等于钻井液的流速时，空心球不再产生滑移现象，两者处于相对静止状态。所以根据空心球的受力和运动过程，建立空心球滑移距离与滑移速率之间的关系如下：

将已知条件代入式(31)中，整理后可以得到滑移距离和滑移速率的关系为：

式中L1为空心球的滑移距离，m；V为钻井液的流动速度，m/s。ρL为钻井液与空心球的混合流体的密度，kg/m3；t为时间，s。

2 空心球滑移速率敏感性分析及室内实验

2.1 深水变梯度钻井空心球滑移速率室内实验

图2为双梯度钻井室内模拟实验系统，其主要包括控制柜(含软件界面和控制器)、模拟钻杆与环空、过滤分离器、液压泵、节流阀、压力传感器等组成。图3为模拟实验系统的原理图。实验时先将空心球与钻井液混合均匀，然后通过液压泵从上部入口处注入，而空心球在过滤分离器处被分离，并从分离口处进入环空中，而其余流体则进入底流口。等待环空中的流动稳定后，每隔t时间测试空心球聚集区的高度,然后将环空中的混合流体排入溢流储液池，钻杆内的流体则进入底流储液池循环利用。根据高度的变化与实验时间得到滑移速率的值，然后通过控制变量法，分别改变钻井液密度、空心球直径、空心球密度以及通过添加聚丙烯酰胺或清水对钻井液黏度进行调节，并重复上述过程，得到了不同情况下滑移速度的测试值，如图4～14所示。

图2 双梯度钻井模拟实验系统Fig.2 Simulation experiment system for dual-gradient drilling

图3 双梯度钻井实验系统原理图Fig.3 Schematic diagram of the experimental system for dual-gradient drilling

图4 不同流态下滑移速度随钻井液密度的变化Fig.4 Variations of the slip rate with drilling fluid in different flow regimes

图7 过渡流时滑移速度随空心球与钻井液密度的变化Fig.7 Variation of slip velocity with the density of HGS and drilling fluid during transition flow

图8 过渡流时滑移速度随空心球密度与直径的变化Fig.8 Variation of slip velocity with the density and diameter of HGS during transition flow

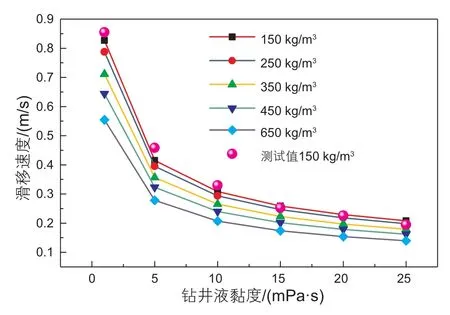
图9 过渡流时滑移速度随钻井液粘度和空心球密度的变化Fig.9 Variation of slip velocity with the density of HGS and viscosity of drilling fluid during transition flow

图10 过渡流时滑移速度随钻井液粘度和钻井液密度的变化Fig.10 Variation of slip velocity with the density and viscosity of drilling fluid during transition flow

图11 过渡流时滑移速度随钻井液粘度和空心球直径的变化Fig.11 Variation of slip velocity with the diameter of HGS and viscosity of drilling fluid during transition flow drilling fluid and diameter of HGSduring Turbulent flow

图13 紊流时滑移速度随钻井液密度和空心球密度的变化Fig.13 Variation of slip velocity with the density of HGS and drilling fluid during transition flow

图14 紊流时滑移速度随空心球密度和空心球直径的变化Fig.14 Variation of slip velocity with the density diameter of HGS during Turbulent flow

2.2 空心球滑移速率的模型计算

根据式(30)所示的滑移速率的数学模型，计算了不同流动状态时的滑移速率。过渡流时的计算结果如图4～11所示；紊流时的计算结果如图12～14所示。由图4和图5可知，在不同流态时，滑移速度随着钻井液的密度增加而增加，随空心球的密度增加而降低，并且随着流体波动的加剧，空心球受到钻井液的曳力增加且空心球的碰撞加剧，所以滑移速度逐渐减小。由图6～14可知，不论空心球在过渡流状态或紊流状态，滑移速度都随钻井液密度、空心球直径增加而增加，而随空心球密度和钻井液黏度的增加而降低。因为钻井液的密度增加，则空心球所受到的浮力增加，相同时间内空心球滑移距离更远，从而滑移速率更大。而空心球的密度不变时，随着直径增加，其所受的浮力与重力之差增加且碰撞频率减小使得空心球颗粒之间的曳力减小，所以空心球的滑移速度增加。而空心球直径不变时，随着密度的增加，空心球所受重力显著增加，因而相同时间内滑移距离减小，滑移速度降低。故在钻井过程中，为了尽量减小因空心球滑移所带来的不利因素，在保证井筒压力处于安全范围的条件下，则需要减小空心球直径，或增加空心球密度和钻井液黏度，从而减小滑移速度。

图5 滑移速度随空心球密度的变化Fig.5 Variations of the glide rate with HGS density in different flow regimes

图6 过渡流时滑移速度随钻井液密度的变化Fig.6 Variation of slip velocity drilling fluid density in transition flow

图12 紊流时滑移速度随钻井液密度和空心球直径的变化Fig.12 Variation of slip velocity with the density of drilling fluid and diameter of HGSduring Turbulent flow

3 井筒压力预测模型及敏感性分析

3.1 井筒压力预测模型

由前所述，空心球的滑移会使得上部环空的混合流体密度变得过小，而下部环空的混合流体密度变得过大。从而导致井筒压力超过窄安全密度窗口，引起溢流或者漏失等复杂情况。所以有必要研究空心球滑移对井筒温度压力耦合场的影响规律。根据式(32)所示，空心球的滑移速率越大，空心球所产生的滑移距离越大。而滑移距离的不同则会改变环空中不同井段的空心球含量和环空流体的密度，最终影响井筒压力的分布。所以本文以空心球的滑移距离来直接表征空心球的滑移速度所产生的影响，从而建立其与空心球体积分数的关系，并进一步研究空心球滑移对环空流体的密度以及井筒温度和压力的影响规律。首先根据双梯度钻井的原理，建立了如图15所示的井筒压力分布的物理模型，然后基于该模型推导了不同钻井状态下的环空压力预测模型如下所示：

图15 双梯度钻井井筒压力预测物理模型Fig.15 Physical model of wellbore pressure prediction during dual-gradient drilling

(1)对于状态A的任意点T的压力计算：

(2)对于状态B的任意点T的压力计算：

(3)对于状态C的任意点T的压力计算：

如果空心球注入的总数量为n，分离器的位置距离井口的深度为L，空心球的滑移距离为L1。根据滑移前后空心球聚集区域深度的变化可以得到空心球体积分数的增量。空心球滑移速度的不同会导致滑移距离发生改变，从而进一步影响轻质段与重质段流体的液柱长度以及轻质段流体的体积分数。假设空心球分离后进入环空的初始状态以及滑移后达到稳定状态时，空心球在钻井液中均匀分布，得到如图16所示的双梯度钻井系统中空心球滑移前后的分布情况。根据上述变量可以得到滑移前后，轻质段流体的空心球体积分数的变化以及环空中混合流体的热物性参数的初始值为：

图16 空心球滑移前后在环空中的分布Fig.16 The distribution of HGS in the annulus before and after sliping

因为在钻井循环过程中，钻井液的热物性参数与温度、压力之间相互影响，所以本文利用多元非线性回归分析方法对McMordie等[17]的水基钻井液实验数据进行处理，得到钻井液的密度与温度、压力的关系式为：

根据滑移前任意状态环空压力预测模型以及滑移后环空中轻质段钻井液的空心球体积分数变化与液柱长度变化，可以得到滑移后随钻井底压力预测数学模型：

其中PT为任意点压力，MPa；A、B、C为3种钻井状态；θ为井斜角，°；ρ为钻井液密度，kg/m3；L、W分别表示轻质段钻井液与重质段的钻井液；ρ0表示轻质段或者重质段流体的初始密度，kg/m3；hL为分离器顶部到井口的距离，m；hW为分离器底部到目标点的距离，m；hj为分离器段的环空长度，m；ε为注入空心球体积分数，%；ψ为过滤分离器分离效率，%；Δε为滑移引起的轻质段体积分数的变化，%；μ为黏度，mPa·s； ΔPf为循环压降，MPa；m,s分别表示钻井液与空心球；H*为随钻井深，m；为分离器到钻头的距离，m；Pcp为回压，MPa；g为重力加速度，m/s2。ρ(T,P)为混合流体随温度压力变化的密度，kg/m3；T0为常温，℃；P为压力，MPa；T为温度，℃。

3.2 敏感性分析

3.2.1 基础数据

首先基于双梯度钻井室内模拟实验系统研究了过滤分离器的分离效率。如图17所示为分离效率的实验结果，分离效率随着钻井液排量的和空心球体积分数的增加而增加，且分离效率的范围为95%～98.5%。因为过滤分离器将空心球过滤后，空心球会短暂停留在过滤结构的球形外表面，随着排量的增加，空心球受到的钻井液的冲刷作用更强，有利于分离出的空心球进入到环空中；而随着空心球体积分数的增加，球-球之间的有效接触面积增加，进一步地减小了钻井液与空心球的接触面积，从而使得钻井液的曳力减小，更有利于空心球的分离。但是因为钻井液黏度的影响，空心球在循环系统中存在黏附与聚集现象，使得部分空心球无法排出，所以随着排量和空心球体积分数进一步增加，分离效率不再增加。

图17 分离效率的实验结果Fig.17 Experimental results of separation efficiency

所以本文选择分离效率为98%，再结合南海某区块深水钻井的数据[18-19]：井深6000 m，水深1500 m，入口温度为15 ℃，地表温度为20 ℃，钻井液排量为0.25 m3/s，地温梯度为0.25 ℃，钻井液密度为 1200 kg/m3,比热为 3900 J/(kg·K)，导热系数为 1.73 W/(m·K)，海水密度为 1050 kg/m3，比热为4130 J/(kg·K)，导热系数为 0.65 W/(m·K)，空心球比热为750 J/(kg·K)，导热系数为0.47 W/(m·K)，机械钻速为3.01m/h。然后基于空心球滑移条件下的双梯度钻井随钻井底压力预测模型进行温压耦合场的数值计算和敏感性分析。

3.2.2 滑移距离

如图18所示，当分离器位置一定时，随着空心球滑移距离的不断增加，随钻井底压力也逐渐增加。因为当空心球的滑移距离不断增加时，轻质段流体的液柱长度不断减少，而重质钻井液段的长度增加，所以随钻井底压力逐渐增加。同理，如图19所示，因为滑移距离的不断增加，轻质钻井液段的长度不断减小；则达到稳定状态后，单位液柱长度所含空心球体积分数增加，轻质段混合流体的密度则不断减小，重质钻井液段的液柱长度增加，但其密度不随滑移距离发生变化，而且在上、下环空的交界面处(分离器位置处)的密度会产生明显的突变。

图18 随钻井底压力随滑移距离的变化Fig.18 Variation of bottom hole pressure with slip distance

图19 混合流体密度随滑移距离的变化Fig.19 Variation of mixed fluid density with slip distance

3.2.3 分离器位置

如图20所示，随着分离器位置从A、B、C变化时，相同井深位置处，随钻井底压力不断减小。因为随着分离器在井深位置的不断增加，随钻井底压力分布曲线的拐点不断下移，使得轻质钻井液液柱的长度不断增加，而重质钻井液的液柱长度不断减少，从而导致随钻井底压力逐渐减小。

图20 随钻井底压力随分离器位置的变化Fig.20 Variation of bottomhole pressure with separator

3.2.4 空心球体积分数与分离器位置

如图21所示，当空心球与分离器的位置同时变化时，分离器位置主要影响环空中轻质与重质流体的液柱长度，从而影响拐点沿井深位置的分布，而空心球体积分数主要影响轻质段流体的密度大小。随着分离器位置的不断增加，密度分布曲线的拐点逐渐下移；而随着空心球体积分数的不断增加，轻质段流体的密度不断减小，重质段流体的密度基本不变，从而使得上、下环空中的流体密度分布在分离器位置处存在突变。

图21 混合流体密度随分离器位置和空心球体积分数的变化Fig.21 Mixed fluid density varies with separator position and volume fraction of HGS

图23 不同滑移距离和空心球体积分数对环空温度的影响Fig.23 Effect of different slip distances and volume fraction on annulus temperature

3.2.5 空心球体积分数与滑移距离

从图22～24中可以看出，当分离器位置和空心球体积分数一定时，随着滑移距离的不断增加，轻质段流体的液柱长度不断减小，而重质段流体的液柱长度不断增加，所以环空流体的密度分布曲线在突变点上部的曲线长度逐渐减小，而下部曲线的长度逐渐增加，从而使得相同井深位置处，随钻井底压力逐渐增加。随着滑移距离的不断增加，重质流体的液柱长度不断增加，所以相同时间内向外界传递的热量增加，从而导致环空温度逐渐降低。而当空心球体积分数增加时，轻质段流体的密度不断减小，所以突变点上部的曲线不断左移。

图22 混合流体密度随滑移距离和空心球体积分数的变化Fig.22 Variation of mixed fluid density with slip distance volume fraction of HGS

3.2.6 分离器位置与滑移距离

图24 随钻井底压力随滑移距离和空心球体积分数的变化Fig.24 Variation of bottom hole pressure with slip distance and volume fraction of HGS

图26 分离器位置一定时不同滑移距离对环空温度的影响Fig.26 The effect of different slip distances on annulus temperature when the separator position is fixed

如图25和26所示，当滑移距离不变时，随着分离器位置的增加，上部轻质段流体的液柱长度会逐渐增加，重质段流体的液柱长度会逐渐减小，使得环空流体密度分布曲线在突变点上部的曲线长度逐渐增加。而滑移距离的增加又会减小轻质段流体的长度，使得轻质段流体密度显著减小，所以密度分布曲线上又表现为在突变点的上方曲线长度逐渐减小，并且逐渐左移。分离器位置一定时，当滑移距离增加，重质段流体的液柱长度逐渐增加，轻质段流体的液柱长度逐渐减小，从而导致相同时间内与外界的传热量增加，所以环空温度逐渐降低。

图25 混合流体密度随分离器位置和滑移距离的变化Fig.25 Variation of mixed fluid density with separator position and slip distance

4 结论

通过碰撞理论建立了空心球的滑移速率模型，然后利用室内实验对模型进行了验证，得到了空心球滑移速率在不同条件下的分布规律。然后基于实验所得分离效率以及滑移速率与滑移距离的关系模型，建立了空心球滑移条件下的双梯度钻井随钻井底压力预测模型，并结合钻井数据进行了数值计算和敏感性分析，得到如下结论：

(1)基于理论计算与室内实验研究表明，空心球的滑移速率随钻井液密度和空心球直径的增加而增加，随钻井液黏度与空心球密度的增加而减小。所以适当减小空心球的直径或增加钻井液的黏度可以减小空心球的滑移可能带来的不利影响。

(2)随着空心球滑移速率的增加，其滑移距离也会逐渐增加，进一步地会引起井底压力逐渐增大。轻质段混合流体的密度和环空温度随着滑移距离的增加而逐渐减小。

(3)分离器位置与空心球体积分数对环空压力有显著影响，随着分离器位置和空心球体积分数的增加，随钻井底压力和轻质段混合流体的密度不断减小，并且环空压力和环空流体密度分别在分离器位置处存在明显的拐点和突变点。