微管流微扰-数值分析与转轴粗糙度检测模型

宋孟天，雷杰超，张建成

(1.广西大学 土木建筑工程学院，广西 南宁 530004；2.广西大学 机械工程学院，广西 南宁 530004)

0 引言

微流控是在微通道中操纵微量流体的运动以达到工程目的的技术，整个系统可集成在厘米级别甚至更小的芯片上，应用领域有热传、微轴承润滑、高通量药物筛选等[1-3]。具有代表性的一种结构是由外圆柱罩和黏性流体包裹的转轴构成的同心圆柱，微尺度下壁面效应大大增强，工作过程中，由于器件之间的相对运动，并且流体存在黏性与腐蚀性，轴的表面会因为沉积、磨损和腐蚀原因变得粗糙[4-6]。表面粗糙度一方面会对微管内流体的流动特性产生影响，改变其工作参数使其不再满足原有的要求，另一方面对轴的机械性能以及作用于其上的力和转矩有极大的影响，给设备的工作状态带来隐患。因此，发展表面粗糙度检测技术极为重要，可为提前判断设备是否需要更换或维修提供依据，避免设备失效破坏造成经济损失。传统的粗糙度检测方法有扫面隧道显微镜法、超声波法和光学测量方法等[7-9],所需设备昂贵。同时，微流控设备中的元件往往被其他的装配单元所包裹，检测时需要进行拆卸，这就使得传统的粗糙度检测技术难以直接应用。因此，需要发展基于流体的粗糙度检测方法。

微流控领域的一个基本问题是粗糙微管内流体的库埃特流动和泊肃叶流动。PONJAVIC等[10]采用荧光漂白恢复法研究了弹流润滑中流体的速度剖面和滑移长度，首次实现全厚度流速的直接测量。郝鹏飞等[11]发现雷诺数较小时，微观粒子图像测速技术本身带有1 % ～ 2 %的误差。姚华平等[12]采用有限差分法求解雷诺方程，研究了两个方向的正弦/均方根随机粗糙表面之间的微流道库埃特流动，其结果表明油膜承载能力随波长以二次曲线的规律变化。XIONG等[13]利用有限体积法求解三维随机粗糙圆管中水流动的Navier-Stokes方程，结果表明主流区域受到粗糙度的强烈影响，泊肃叶数偏离高达11.9 %，刘赵淼等[14]也得到类似的结果。

在解析解的研究上，WANG等[2]利用边界摄动法研究具有周向正弦表面粗糙度的两同心圆柱间的库埃特流，最早得到内旋转轴上的力和转矩，此外，还利用边界摄动法研究了具有两个方向表面粗糙度的圆管泊肃叶流，表面粗糙度利用正弦函数的乘积来模拟[15]。SONG等[16]用余弦波、矩形波和三角波模拟圆管轴向壁面粗糙度，采用边界摄动法推导泊肃叶流解析解，但是所研究的是单一方向的粗糙度。

以上文献报道的表面粗糙度模型多为一个方向，不能真实全面体现实际粗糙度的影响。两个方向上的粗糙度虽有研究，但研究的是圆管内的流动，对于几何结构较为复杂的两圆柱之间的微管流，周向和轴向粗糙度同时存在的情况尚未考虑。另外，以上成果集中在粗糙度对流体流动特性的影响上，很少根据流体参数反推粗糙度。本文通过精确到二阶的边界微扰方法，研究微管内转轴表面两个方向的粗糙度幅值和疏密程度对轴上的转矩和流体流率的影响，以此提出一种新的表面粗糙度检测模型。利用计算流体力学软件COMSOL进行数值模拟，仿真结果和理论结果呈现良好的一致性。在此之前，本课题组已开展了表面粗糙度的相关微扰解析工作[17]，本文则进一步以数值计算承接解析的思路，验证解析解，并拓展粗糙度检测模型的应用范围。

1 物理模型与基本方程

图1表示两个同心圆柱，内轴粗糙，外圆柱罩光滑。微流控设备在工作时，实际是内轴转动，例如：内轴以角速度Ω绕z轴顺时针旋转，流体则因壁面摩擦力被驱动形成库埃特流动，如图1(b)所示。当内轴上存在不同形式和大小的粗糙度时，其上的转矩因此而变化，此问题是非稳态的。本文的目的是为了检测转轴表面粗糙度，而轴上受到的转矩与外圆柱罩上受到的转矩相等，因此为了便于计算，将内粗糙轴固定，使外光滑圆柱沿相反方向以同样的角速度旋转，则问题变为稳态，且外圆柱可以较低角速度Ω′旋转，以便于进行层流分析，即为本文所求解的等价问题，如图1(c)所示。此外，为了达到检测轴表面粗糙度的目的，本文另一研究内容是让设备静止，即内轴和外圆柱都没有旋转，在微管间隙的两端施加压力差形成泊肃叶流动，研究内轴表面粗糙度对流率的影响，从而得到更全面的信息以建立转轴表面粗糙度模型。

外圆柱和内粗糙轴半径分别为R与r*[17]，

(1)

其中：Rb(b<1)为内轴的平均半径，ε为轴的粗糙度幅值与其平均半径之比，λz为z*方向即轴向的波长。

以外圆柱半径R为特征长度进行无量纲化，取外圆柱无量纲半径为R=1，则内轴无量纲半径为

r=b+εcos(nθ)cos(αz)=b+εg(θ,z)

(2)

其中：n=2πR/λθ，α=2πR/λz，分别为周向θ和轴向z方向上的波数，λθ为θ方向上的波长。

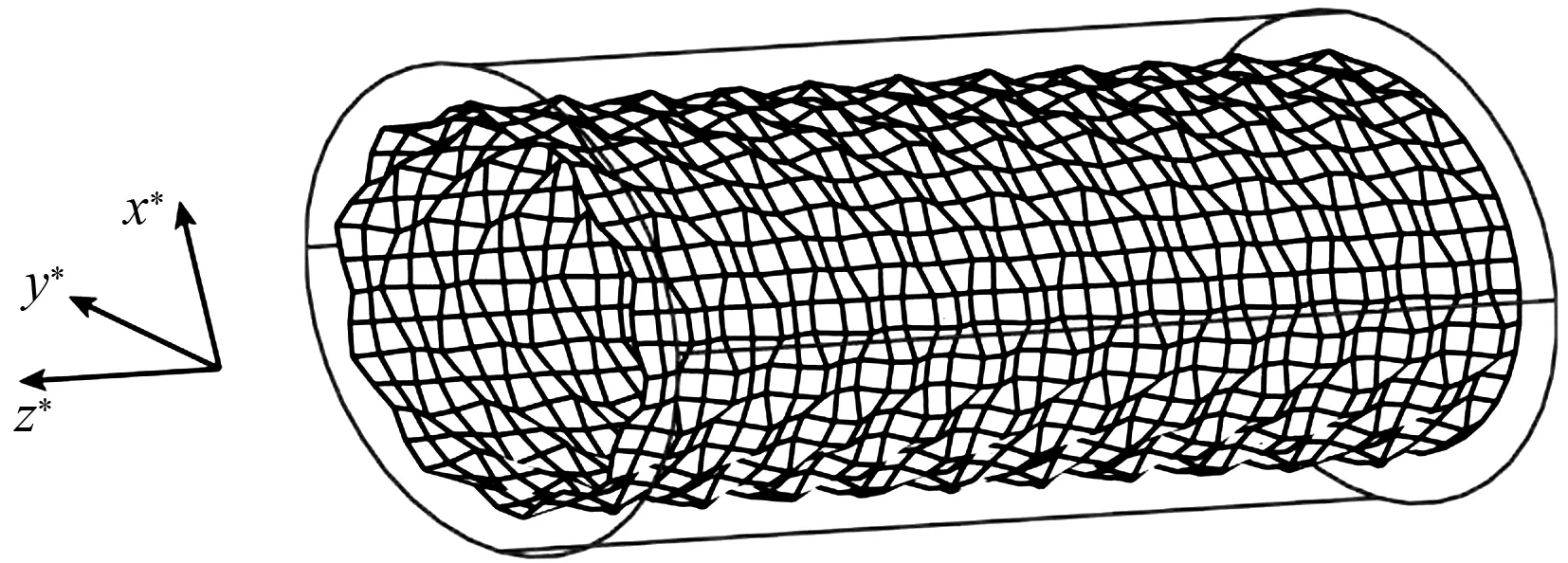
(a) 物理模型立体图

(b) 原始问题：Ω为工作时转轴角速度

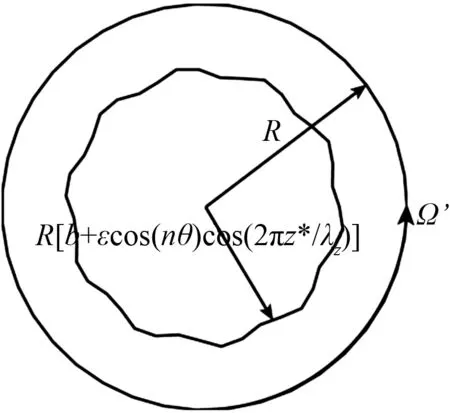
(c) 等价问题：Ω′为检测时外圆柱罩角速度

对稳态不可压缩黏性流，连续方程为[18]

*·u*=0，

(3)

其中：u*=(u*,v*,w*)为流场速度向量，u*，v*和w*分别为径向、周向和轴向的速度分量。动量方程为[18]

ρ(u*·*)u*=-*p*+μ*2u*，

(4)

其中：μ为流体动力黏度，p*为压力，ρ为流体密度。

2 微扰分析

2.1 库埃特流动

以U=Ω′R为特征速度，μU/R为特征压力，则无量纲化的速度、压力分别为：u=u*/U=u*/(Ω′R)，p=p*/(μU/R)。因此，连续方程式(3)和动量方程式(4)分别变为

·u=0，

(5)

(6)

小转速下，旋转雷诺数ReΩ≡ρΩ′R2/μ远小于1，因此式(6)左侧项可忽略，得到斯托克斯方程

2u=p。

(7)

将速度与压力项进行精确到二阶的微扰展开[17]，得

(8)

由于内轴固定，外圆柱旋转，r=b+εg处的无滑移速度边界条件为

(9)

r=1处的边界条件为

(10)

其中：速度u的下标0、1、2分别表示零阶、一阶和二阶速度。

零阶边界条件(ε=0)：

u0|r=b=u0|r=1=0,v0|r=b=0,v0|r=1=1,w0|r=b=w0|r=1=0。

(11)

一阶边界条件：

(12)

二阶边界条件：

(13)

零阶解：

(14)

压力为常数，因此压力梯度为零。为了简便，我们取p0=0。

一阶解：

(15)

其中

超声波测距模块用来测量模块距离地面的距离d;MPU-9250模块用来测量拐杖运动的角速度w。通过大量的实验来模拟老人摔倒时的状况,发现当d>240 cm、w>5 rad/s且最终测量角度大于80°时,有99.2%的情况老人处于跌倒状态,将此作为判定老人跌倒的标志[9],同时控制GSM模块将报警信息发送至远程的手机监测软件,其软件流程如10所示。

(16)

式(16)中：In和Kn为n阶修正贝塞尔函数。

对于转矩的计算，周向速度是主要贡献，因此只给出V1c(r)的表达式，其余三项U1c(r)，W1c(r)和P1c(r)也是修正贝塞尔函数的组合，A1、B1、C1、D1、E1和F1为待定系数，根据边界条件确定。

二阶解：

(17)

其中：U2α，W2α和P2α均为零，V20(r)=A2I1(2αr)+B2K1(2αr)。

平均转矩：

由于对称性，有

(18)

对θ积分后平均速度为

(19)

(20)

外圆柱上单位面积的平均转矩为

(21)

为了简便，可以取αz1=π/2，αz2=3π/2，同时内粗糙轴上的平均转矩与外圆柱上的转矩大小相等，方向相反，因此有内轴上的转矩为

(22)

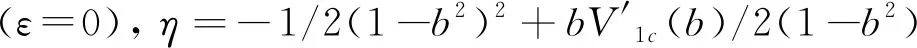
M*=μΩ′R3M=μΩ′R3[M0+ε2η]。

(23)

在θ和z方向上均覆盖一个波长的区域面积，可由下式给出

Sc=(2π)2/(nα)=(2π)2/Ac，

(24)

因此，Ac=nα可称为粗糙度密度，通过定义粗糙度密度，可综合分析波数n和α带来的影响。以b=0.5，ε=0.05为例，平均转矩M随n和Ac的变化如图2所示。可见当n取1和2时，M随粗糙度密度Ac的增加而增加，当M取到最小值，即Ac=20时，n和α的组合为(3, 20/3)；而当n大于等于3时，平均转矩M基本不随Ac的变化而变化。

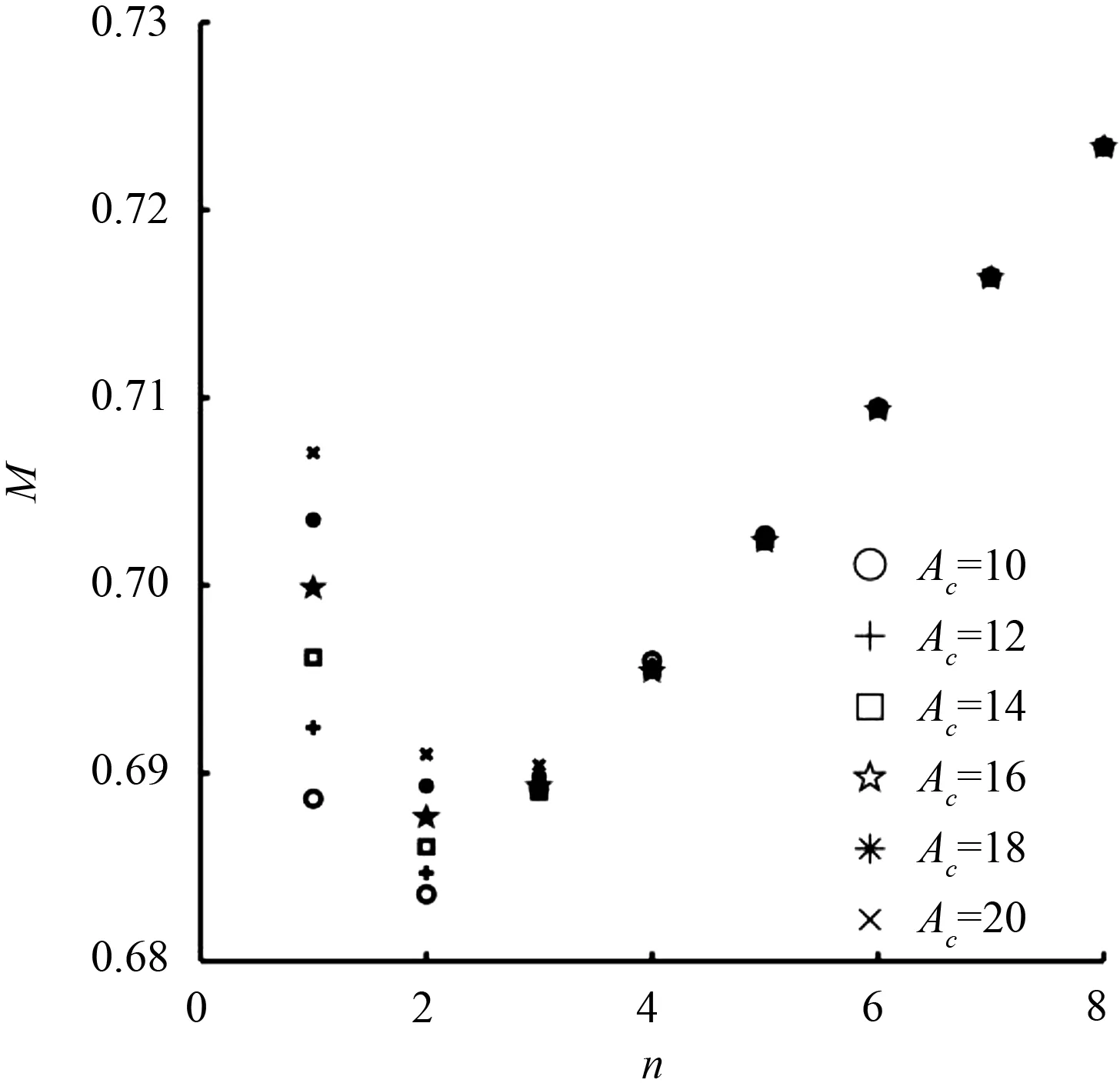
图2 b=0.5，ε=0.05时平均转矩M随n和Ac的变化情况Fig.2 Variation of the mean torque M versus n and Ac (b=0.5, ε=0.05)

2.2 泊肃叶流动

内粗糙轴和外光滑圆柱静止，微管间隙两端施加压力差G，问题为稳态且流动为单方向，因此式(4)左侧项为零。以G为特征压力，GR2/(4μ)为特征速度对连续方程式(3)和动量方程式(4)进行无量纲化，得

(25)

无滑移边界条件为

(26)

零阶边界条件(ε=0)：

u0|r=b=u0|r=1=0,v0|r=b=v0|r=1=0,w0|r=b=w0|r=1=0。

(27)

一阶边界条件：

(28)

二阶边界条件：

(29)

零阶解：

(30)

一阶解：

(31)

其中

(32)

对于总流率的计算，轴向速度是主要的贡献，因此只给出W1c(r)的表达式，其余三项U1c(r)，V1c(r)和P1c(r)也是修正贝塞尔函数的组合。

二阶解：

(33)

同样地，只给出W20(r)的表达式：

(34)

总流率：

总流率可写为

(35)

微管中任意界面流率相同，为了简便，令z=π/(4α)，则W2α项积分为零，式(35)变为

(36)

其中

(37)

Q0为粗糙度为零时的流率，χ为粗糙度对总流率产生的净效应。可见，微管中的总流率被ε二阶修正。

有量纲的流率为

(38)

与库埃特流动一样，以b=0.5，ε=0.05为例，总流率Q随n和Ac的变化如图3所示。可见对于同样的n值，当粗糙度密度Ac增加，即波数α增加，总流率Q随之减小；n变大时，总流率Q随Ac变化的减小趋势放缓。当Q取到最小值，即Ac=3.5时，n和α的组合为(2, 1.75)。

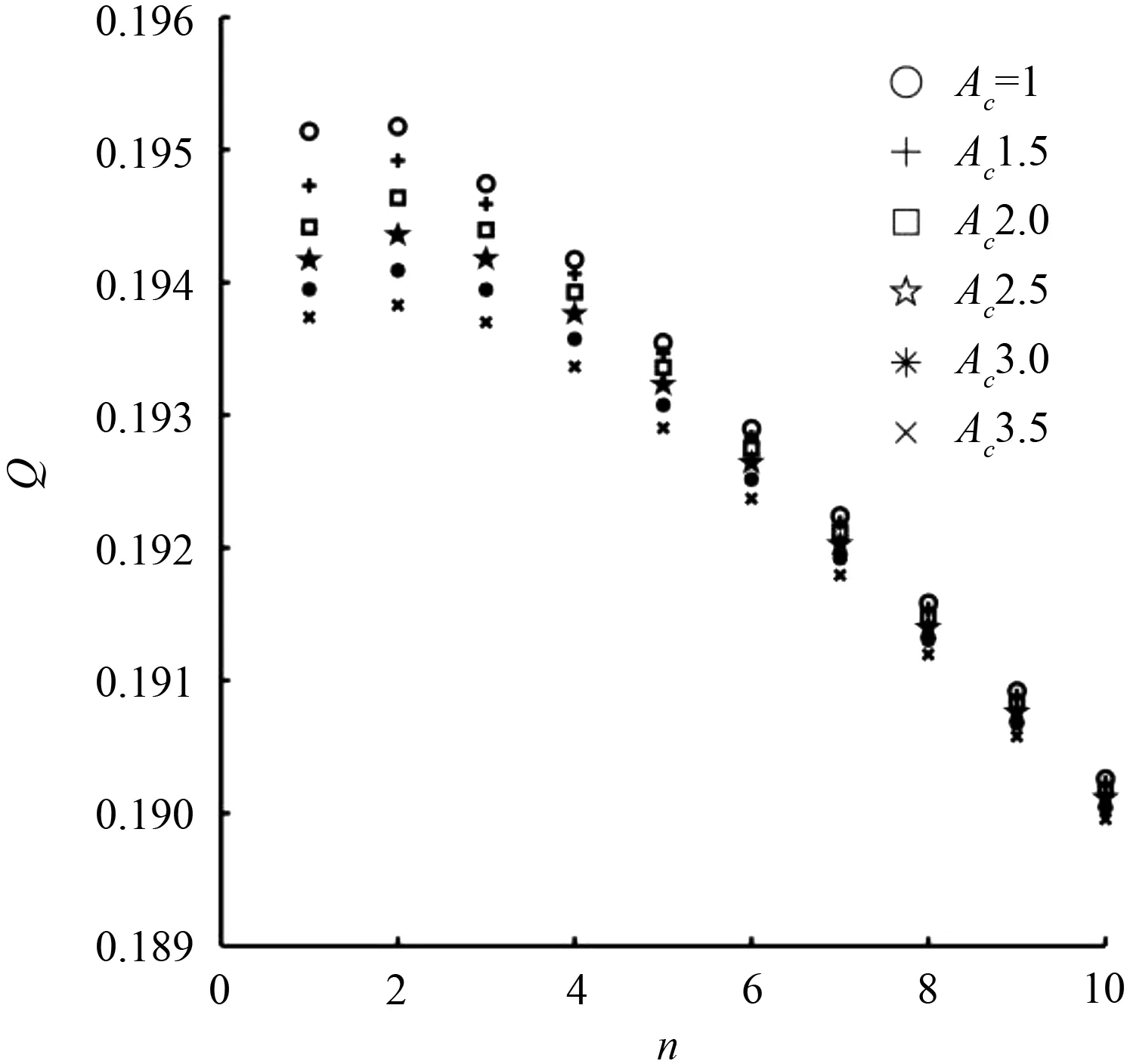
图3 b=0.5，ε=0.05时总流率Q随n和Ac的变化情况Fig.3 Variation of the total flow rate Q versus n and Ac (b=0.5, ε=0.05)

3 数值验证与拓展

为了验证理论结果的有效性，本文使用CFD软件COMSOL进行数值模拟，采用方法为有限元法。外圆柱和内粗糙轴为壁面，均为无滑移边界条件。外圆柱半径为1×10-4m，计算域的轴向长度为一个粗糙度波长，即2πR/α，流动介质为水。边界设定和网格如图4所示。

(a) 库埃特流动设定

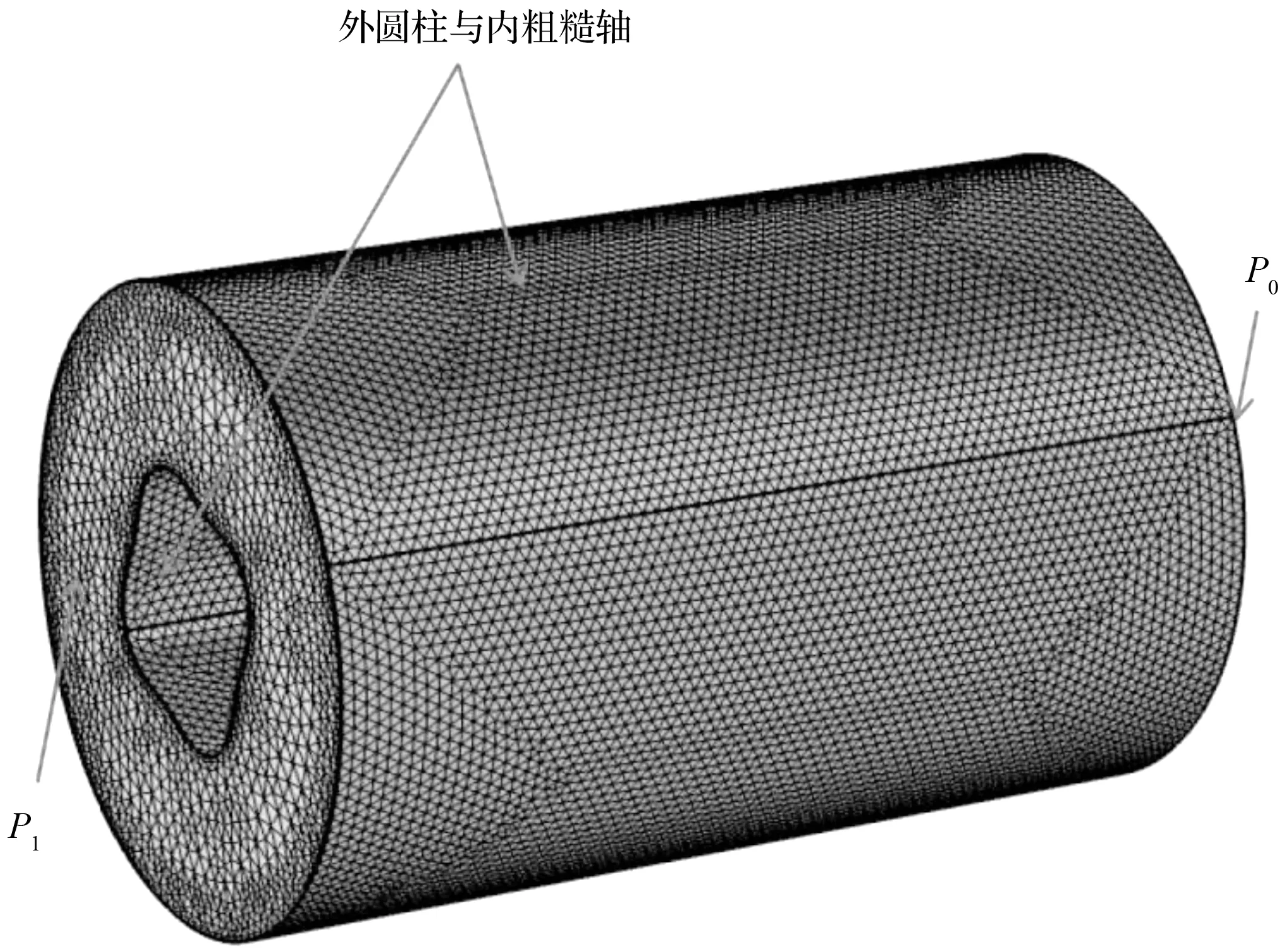
(b) 泊肃叶流动设定

以b=0.5，ε=0的情况为例，进行网格无关性验证，结果见表1和表2。可见当网格加密到一定程度时，所得结果很接近。因此，对于库埃特流动，选择normal网格类型；对于泊肃叶流动，选择finer网格类型。库埃特流的转矩计算只需在外圆柱表面积分，而泊肃叶流的流率计算需要在微管截面进行积分，因此泊肃叶流内部网格需要划分得更加密集，才能得到更准确的结果。

数值模拟的参数设定为：粗糙轴半径b=0.2，0.4，0.5，0.6，0.7，0.8，粗糙度幅值ε=0，0.01，0.025，0.050，0.1，0.150，0.200。对于库埃特流动，对应的(n,α)值的组合分别为(2, 10)，(2, 10)，(3, 20/3)，(3, 20/3)，(3, 20/3)和(2, 10)。对于泊肃叶流动，(n,α)值的组合分别为(4, 2)，(4, 2)，(2, 1.75)，(3, 7/6)，(4, 2)和(8, 1.5)。微扰分析和数值模拟的结果对比如图5所示，可见，库埃特流动中粗糙轴受到的转矩M随着轴半径b和粗糙度幅值ε的增加而增大，而泊肃叶流动中的总流率Q则相反。这是因为当b和ε逐渐增大时，粗糙轴与外圆柱之间间隙变小，壁面效应变得更加显著。而对于泊肃叶流动，b和ε越小，间隙越大，因此流体流率越大。当ε=0，0.010，0.025、0.050和0.100时，两者之间误差较小。当ε> 0.1时，误差逐渐增大，说明此时边界微扰法已不再适用。这是因为ε过大，一阶和二阶解的绝对值更加接近零阶解，使得微扰解失去了有效性。

因此，边界微扰法的适用范围为粗糙度幅值ε在0到0.100之间。ε=0.150，0.200和0.250时，库埃特流动和泊肃叶流动的数值延伸结果如表3和表4所示，以拓展粗糙度检测模型的应用范围。b=0.8时，由于尺寸限制，只计算到ε=0.200。

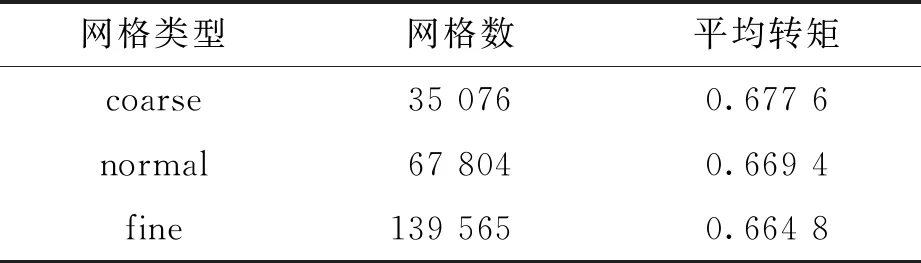
表1 库埃特流动网格无关性验证Tab.1 Grid independence verification of Couette flow

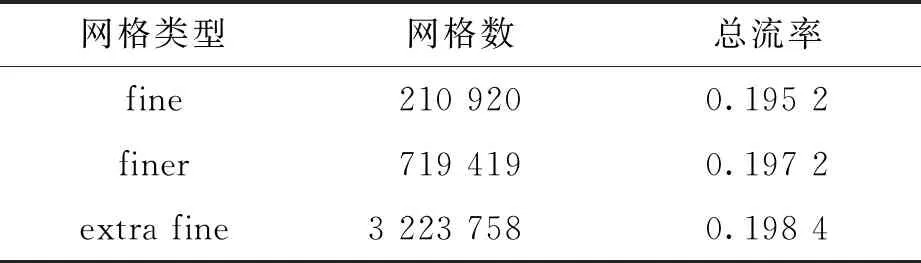
表2 泊肃叶流动网格无关性验证Tab.2 Grid independence verification of Poiseuille flow

(a) 库埃特流动转矩M对比图

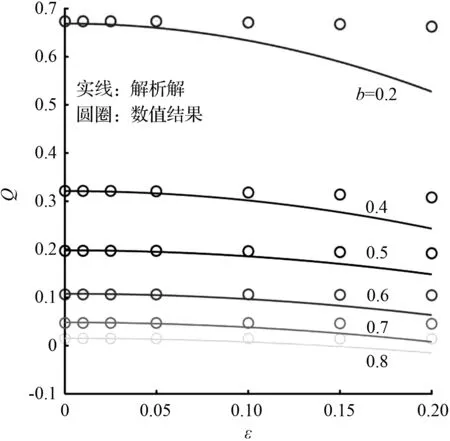
(b) 泊肃叶总流率Q对比图

表3 不同b和ε下库埃特流动无量纲转矩数值结果Tab.3 Non-dimensional numerical simulations torque results of Couette flow under different b and ε

表4 不同b和ε下泊肃叶流动无量纲流率数值结果Tab.4 Non-dimensional numerical simulations flow rate results of Poiseuille flow under different b and ε

4 粗糙度检测模型

首先必须指出，转轴和外圆柱之间的间隙固定，即b是已知的，因此M0和Q0易于计算。由此，基于平均转矩M和总流率Q的导出表达式(22)和(36)，在实践中，结合测量结果，建立了表面粗糙度预测模型

(39)

对于给定的b值，粗糙轴不同的ε，n和α值得到不同的平均转矩M和总流率Q。以b=0.5为例，不同粗糙度下(ε=0.01, 0.05, 0.08, 0.1)n和α变化时的M和Q值如图6所示。由于平均转矩M和总流率Q由实际测量得到，因此可以反推出ε和n的值，并得到α的值。例如，图6中的星号处M=1.111 0，Q=0.118 2，此时ε=0.1，n=12，α=27。此时，如果外圆柱半径为R=1×10-6m，则表面粗糙度幅值为ε×bR=0.1×0.5×10-6m=5×10-8m。不同的n和α的值组合下，M或Q值可能为相同的值，但这种情况对于M和Q不会同时发生，因此n和α的值可以唯一确定。又如，对于数值拓展部分，若M=0.754 7，Q=0.177 9，此时ε=0.2，n=3，α=20/3，如果外圆柱半径为R=1×10-6m，则表面粗糙度幅值为ε×bR=0.2×0.5×10-6m=1×10-7m。

此外，可单独使用库埃特流进行表面粗糙度检测。对于同一种流体，有量纲转矩随着转速Ω′线性增大。由图6(a)及式(39)可知，若测试两种不同转速下的轴上的转矩，必定对应于相同的n和α，然后根据转矩的大小确定相对粗糙度ε。类似地，对于泊肃叶流动，对于同一种流体，有量纲流率随着压力差G线性增大。由图6(b)及式(39)可知，若测试两种不同压力差下的流率，必定对应于相同的n和α，然后根据流率的大小确定相对粗糙度ε。

(a) 平均转矩M随n和α的变化图

(b) 总流率Q随n和α的变化图

5 结语

本文针对粗糙度沿周向和轴向分布的转轴和外光滑圆柱罩之间微管的液体微流动，以粗糙度幅值为扰动项，求解了Stobes方程的解析解，得到了不同半径下，库埃特流动中粗糙轴受到的转矩M和泊肃叶流动中的总流率Q随粗糙度幅值和波数的变化规律。结果表明，转矩M随着轴半径和粗糙度幅值的增加而增大，而总流率Q则相反。通过COMSOL软件进行数值模拟，验证了解析解的准确性，并拓展了应用范围。基于以上结果提出了利用流场参数反推表面粗糙度的方法。

本文的创新点在于，引入周向和轴向两个方向的粗糙度模型，将两圆柱间微管流边界微扰理论推广到二阶，提出了基于流体方法的粗糙度检测模型与检测方法，所检出的粗糙度可视为整体表面的平均，同时采用数值方法拓展了模型的应用范围。本文的结论可用于微流控设备表面粗糙度的不拆卸快速检测。