一种带CPL的Boost PFC新型恒压控制策略
李刚,邱伟,李舒维,廖小花
(1.广西大学 电气工程学院,广西 南宁 530004;2.中国石化销售有限公司华南分公司,广西 南宁 530022)
0 引言
功率因数校正(power factor correction, PFC)是电力电子领域的重点研究内容[1-4]。近些年反馈线性化控制受到学者们的广泛关注[5-8],其用于功率变换器的恒压输出简便有效。Buck型变换器的恒功率负载(constant power load, CPL)在自身内部的开关管关断时会直接影响此类控制策略的连续性,控制律不能正常计算,导致无法恒压输出。有CPL上额外并入电阻能够改善这一问题[9],但是会增加电路的功率损耗。文献[10-13]提出了虚拟阻尼法可以对问题参数进行补偿,通过补偿参数进行调节从而使电压恒定输出。文献[14]提出了一种新的无源控制器设计方案。但文献[10-14]的方案在电路发生大信号扰动时,需对问题参数进行重新优化,不适用于反馈线性化的改进。
文献[15]对CPL系统提出了滑模控制三阶模型思路,在产生大扰动时具有较好的性能。文献[16]运用反馈精确线性化的方法解决了CPL系统中大信号扰动不稳定的问题。文献[17]通过输入输出线性化的方法,对非最小相位系统的CPL变换器在稳态工作点附近做线性化近似处理,由零极点的分布情况得到了新的控制策略。文献[18]提出了将反馈精确线性化与PI结合的控制思路。上述方法虽然能使系统在动态时保持良好的输出特性,但是控制律缺乏对负载变化的预判环节,因此系统的输出响应较慢。
本文以Boost PFC变换器接CPL作为研究对象,通过状态空间建模得到输入输出线性化的控制策略。并对该控制律在带CPL时电路无法恒压输出进行了分析。从控制律参数中输出电流不连续性入手,为加快系统在负载功率大信号扰动的响应速度,通过输出电压纹波对功率变化做出预判,推导出功率和输出电压纹波的函数关系,从而得到新的控制算法。仿真和实验表明,负载在基准功率120 W稳态情况以及跳变至240 W时,该控制律能够迅速判断出功率发生变化并做出调节,使输出电压保持恒定值250 V,整个过程系统始终保持优良的动静态特性。
1 Boost PFC带恒功率负载的状态空间模型
当Boost变换器接入一个Buck负载时,在Buck采用闭环控制的情况下,其相对于前级Boost PFC变换器而言可以等效成一个CPL[19]。图1为Boost PFC恒功率负载拓扑结构图。

图1 Boost PFC恒功率负载拓朴结构图Fig.1 Structure diagram of Boost PFC constant power load
图1中,令整流后的输入电压为vin,经过电感的电流为iin,输出电压为vo,iin和vo两者取开关单周期内的平均值,d为控制MOS管Q的占空比,iout为输出电流。由状态空间表达法对其进行数学建模,结果如下
(1)
在式(1)由Boost拓扑结构通过状态空间平均法建立起来的数学模型基础上,定义该系统状态变量为xT=[x1,x2]=[iin,vo],令输出变量为y=h(x),由此可以得出该系统单输入、单输出的具体数学模型
(2)
2 Boost变换器带恒功率负载控制策略的设计
2.1 单输入、单输出非线性系统可线性化的条件
对于式(2)的单输入、单输出非线性系统,如果有∀x∈Ω,满足以下条件
(3)
则称该系统在Ω上的相对应的阶为r,也称其输出函数y=h(x)对式(2)的系统有r阶的相对应,且满足
(4)
由式(3)、(4)可知,如果该系统的控制输入变量函数与其输出函数建立起联系,那么该系统在Ω上相对应的阶为r,则其输出函数h(x)也需要微分r次。
对式(2)描述的系统,如果该系统对应的阶n与其输出函数h(x)相对应的阶r存在n=r的关系时,那么该非线性系统一定可以通过新的坐标变换使其精确线性化为新线性系统。即式(2)的系统模型只有在满足式(3)和(4)的条件下,该非线性系统才能够完全精确线性化。
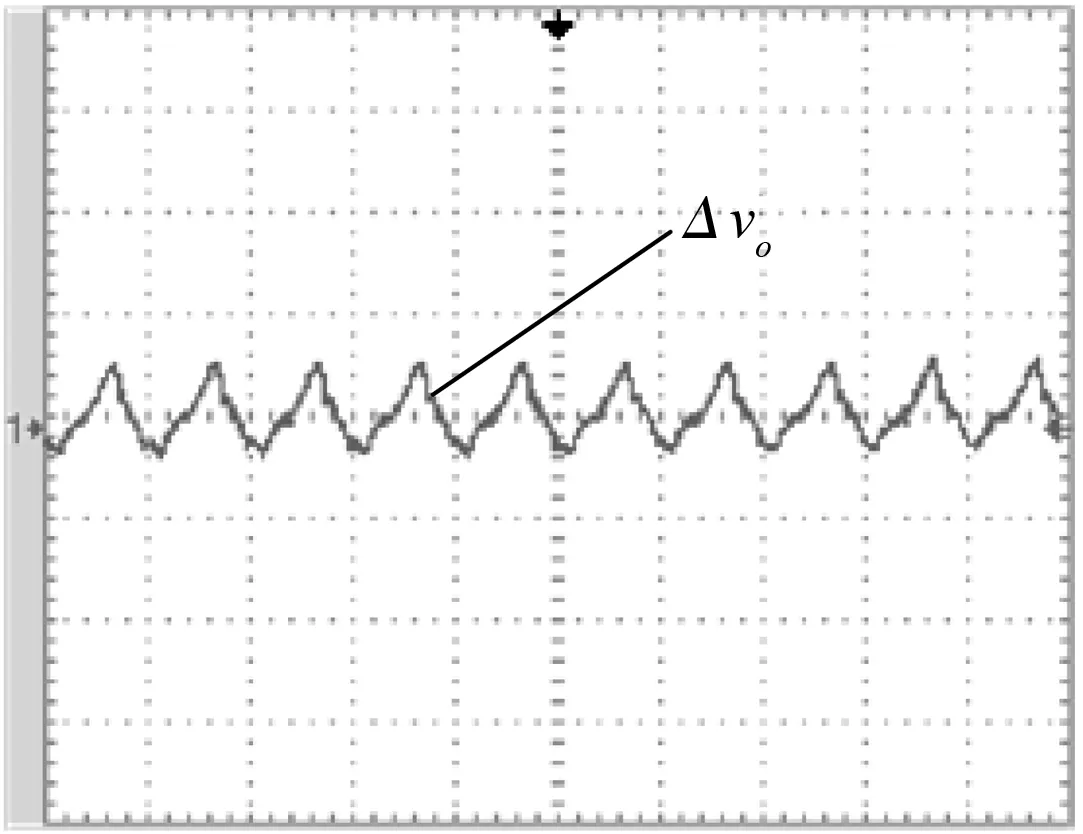
若输出函数h(x)的阶与系统在Ω上相对应的阶的关系是r 在理想状态下不考虑开关管以及一些其他功率损耗时,可以认为系统的输入功率Pin与输出功率Pout是相等的。其次功率因数校正的主要目的是使该Boost电路的输入电流其相位能够准确地跟踪输入电压并使二者的相位能够保持一致性。设期望输出电压和期望输入电流分别为Uref和iinref,校正后的输入电压峰值为Vm;电流峰值为Im,系统的输入功率Pin可以表示为 Pin=0.5Vm×Im。 (5) 根据Pin=Pout的关系,设输出电压为vo,可以确定系统的输出电流为 (6) 上述式(2)的系统通过期望输入电流和电压描述时,系统的状态方程如式(7)所示: (7) 结合上述,式(2)所描述的非线性系统只有在满足式(3)、(4)的约束条件下,原系统才能够完全精确线性化,因此根据式(2)的单输入、单输出非线性系统模型,结合式(3)、(4)进行进一步具体计算分析。 (8) (9) 由式(8)、(9)可知,系统相对应的阶r=1≠n,所以原非线性控制系统只能部分精确线性化。令Span{g(x)}是(5)式中选取的g(x)构成的一个分布,由于它是对合的,通过福诺宾纽斯定理知该系统存在1个标量函数ψ(x)使得式(10)成立。 Dψ(x)·g(x)=Lgψ(x)=0。 (10) 文献[20]表明,上述系统的零动态响应是稳定的。因此对于该系统可线性化的部分,选用如下的非线性坐标变换 (11) 由式(11)所述的坐标变换可知,式(7)中所描述的非线性系统中可作部分精确线性化处理,如下所示: (12) 令 (13) Lfψ(x)=Lfψ(Φ-1(z))=q(z)。 (14) 因此式(12)可以变换成式(15)所表述的准线性系统: (15) 式中:v选取v=-kz1(k为正常数)。 根据式(13)和v=-kz1可以推算得到新坐标与原坐标系之间的控制律关系,如下: (16) 综上所述,由(7)、(8)、(11)代入(16)可得Boost PFC变换器在CPL下控制律为 (17) 图2为起始负载功率120 W条件下,根据式(17)的控制律,对该控制律中各参数点通过直接测量采样计算得到的仿真波形图。图2(a)为输出电流波形,显然CPL自身的MOS管在关断时,电路中没有输出电流通过,电流在整体上呈现不连续的状态,因此上述的控制律在无输出电流流过时无法给出正确的计算结果。图2(b)为输出电压仿真图,控制律受输出电流不连续特性的影响,电路的输出电压在控制过程中产生较明显的波动,最终不能保持恒压输出。 (a) 输出电流波形图 (b) 输出电压波形图 通过对图2中电流不连续问题分析可知,需要对式(17)控制律中输出电流参数的不连续性进行改进,以确保改进后的输出电流变量具有连续性,从而使控制算法能够正常计算。图3表示的是基于式(17)的控制律,负载由起始功率120 W跳变至240 W时输出电流未经修正的输出电压纹波图。针对上述问题,为得到连续的输出电流,同时加快系统响应速度,在控制律中加入负载功率变化的预测函数。根据图3中纹波变化情况,可以将Boost电路的输出电压纹波幅值变化作为判定功率变化的依据。 图3 输出电压纹波图Fig.3 Ripple diagram of output voltage 图4 f(ΔVn, Pn)函数曲线图Fig.4 Function curve of f(ΔVn, Pn) 基于负载功率预测函数的计算,是通过纹波幅值大小来确定系统当前功率,二者结合得到纹波与功率的函数关系式,再由该函数进一步计算输出电流。因此首先要确定纹波变化与功率的数学关系,如图3中参数所示。设起始功率单个周期纹波波峰为最大值Vmax,波谷为最小值Vmin0,其输出电压纹波幅值变化为ΔV0=Vmax-Vmin0,功率突变后其最大值Vmax不变,取跳变后半个周期处的输出电压波形的值为Vmin1,其幅值变化为ΔV1=Vmax-Vmin1,纹波幅值对应的功率为Pn。图3中,显然ΔV1>ΔV0,由此可以判断出系统的负载功率发生了变化。根据此规律对100 W~250 W功率下的输出电压纹波幅值ΔVn和对应的参考功率Pn做数学拟合, 得出纹波变化ΔVn和参考功率Pn的数学关系式:f(ΔVn,Pn)=15.117 0×ΔVn+84.870 4,如图4所示。 将f(ΔVn,Pn)作为电路功率变化的预判函数,Boost电路在工作时输出电压产生的纹波大小ΔV,由f(ΔVn,Pn)比较不同的幅值ΔV判断出电路的当前负载功率,根据当前功率确定相应的输出电流变量,运算流程图如图5所示。用该方法得到的输出电流变量不受CPL自身MOS管的通断影响,因此式(17)中的输出电流参数具有连续性,保证了控制律的正常计算。 图5 运算流程图Fig.5 Flow chart of operation 综上所述,Boost PFC变换器电路在恒功率负载条件下的控制律如式(18)所示: (18) 进一步整理得 (19) 本控制律采用PSIM作为仿真平台,系统具体的仿真参数见表1。 表1 系统仿真参数Tab.1 System simulation parameters 图6为起始功率120 W,由式(19)控制律仿真得到的输出电压和输出电流波形图。图6(b)中的输出电流由函数f(ΔVn,Pn)计算得到,数值为0.48 A。结合式(5)、(6),在输出功率120 W与期望电压输出值为250 V的条件下,输出电流理论计算值为0.48 A,图6(b)的仿真数值与理论计算值一致。由图6(a)的实际输出电压波形可以看出,图6(b)中的输出电流不仅能够使此占空比的控制律算法正常计算,在此基础上系统能够快速调节输出电压,电路输出电压在短时间内达到250 V,与期望输出电压保持一致。以上分析表明,f(ΔVn,Pn)函数不仅能够准确得到连续的输出电流,而且通过对系统功率预测的方式提高了电路的静态响应特性。 (a) 输出电压波形图 (b) 输出电流波形图 图7 负载功率120 W跳变至240 W时 输出电流波形图 Fig.7 Output current waveform when the load power is 120 W and jumps to 240 W 图7为CPL负载功率120 W在1 s跳变至240 W时,由f(ΔVn,Pn)计算得到跳变前后的输出电流波形。图7中看到,跳变前的输出电流为0.48 A,在功率产生跳变时f(ΔVn,Pn)能立即判定功率变化情况,并给出功率跳变后的输出电流值为0.96 A,相比跳变前增大了一倍。同理根据式(5)、(6)可知,期望输出电压为250 V的条件下,跳变前后的输出电流理论计算值为0.48 A和0.96 A。图7的仿真数值与理论计算值相等。由此可看出该算法在具备静态快速响应特性的同时,对于系统产生扰动时在输出电流的计算上仍然表现出良好的准确性。 图8为负载功率120 W在仿真时间1s跳变至240 W输出电压波形图。图8(a)为输出电压整体的示意图。由图8(a)看出,负载功率在跳变后,电路的输出电压能够继续维持恒压输出,跳变后输出电压仍然为250 V,与期望输出电压值保持一致。图8(b)为1 s处跳变点前后的部分电压放大图。基于图8(b)看出,负载功率发生跳变后,输出电压纹波大小在数值上有相应的变化,在跳变时系统经过极短时间微调后继续保持恒压输出。上述表明,控制律通过加入功率预判函数能够对电路功率变化迅速做出判断和精准调节,使电路功率变化后输出电压快速达到恒压输出。当系统功率发生跳变时,文中式(19)的控制律与文献[16]提出的控制律相比,其动态响应在超调量、稳定性以及快速性方面明显优于后者。 (a) 负载功率跳变时输出电压波形图 (b) 负载功率跳变时输出电压放大波形图 图9为负载功率120 W在1 s跳变至240 W的情况下,Boost变换器未经整流桥的输入电压与输入电流的波形图。结合表1与图9可以看出,交流型的输入电压峰值为150 V。输入电流在负载功率跳变前后,其相位都能够准确地跟踪输入电压,因此系统具有功率因数校正的特点。负载功率跳变前,其输出电流峰值为1.6 A,功率在1 s发生跳变时,输入电流峰值在原来电流值的基础上立即增大了一倍,整个电流变化没有明显的过渡过程。 图9 负载功率120 W跳变至240 W时Boost输入端电流与电压波形图Fig.9 Waveform of current and voltage at boost input when load power changes from 120 W to 240 W 为进一步验证该控制律的正确性,通过搭建了一台最大输出功率为300 W的实验样机进行实验验证。主功率电路参数同仿真参数一致,控制芯片为DSP系列TMS320F28335。 图10为实验样机在起始负载功率120 W时的输出电压波形。从图10(a)的整体图可以看到在起始负载功率120 W的情况下输出电压为250 V,稳态性能良好。图10(b)为输出电压纹波示意图,可看到输出电压纹波的幅值大小较为明显,因此f(ΔVn,Pn)函数可以通过纹波变化准确识别出系统负载功率大小,稳态下的输出电压特性验证了与仿真的一致性。 (a) 输出电压总体示意图 (b) 输出电压纹波 图11为实验样机经过PFC以及整流后的输入电流与输入电压波形图。图11(a)为起始负载功率由120 W跳变至240 W的波形,从图11(a)可以看到,输入电压峰值始终保持在150 V的同时,功率在突变的瞬间输入电流峰值立即由1.6 A跳变为3.2 A,由此说明控制律具有快速响应特性。根据式(5)和图11(a)可知,系统的输入功率跳变后为240 W,由输入、输出功率相等的关系可得到系统此时的输出功率为240 W。图(b)为负载功率240 W稳态下系统的输入电压和电流波形图。稳态时,系统的输入电压峰值仍然保持150 V,输入电流峰值为3.2 A,输入电流总体上呈现出准确地跟踪输入电压的特点。通过对图11分析得知,系统的负载功率在发生跳变的情况下,控制律能够快速判断出功率的变化情况,进而调节输入电流并产生相应的变化,通过调节使输入电流准确地跟踪输入电压,呈现出良好的功率因数校正特性。 (a) 跳变前后输入电压与输入电流波形图 (b) 240 W稳态时的输入电压与电流波形图 图12为起始负载功率120 W跳变至240 W时系统的输出电压波形图。图12(a)为输出电压整体波形图,从图(a)中看出,负载功率发生变化时,控制律在准确判断后做出调节,输出电压总体上维持恒压输出的状态。图(b)为功率240 W稳态下输出电压纹波示意图,对比图10(b)的电压纹波,图12(b)电压纹波幅值比图10(b)的大,由此可以根据纹波变化这一特性判断出负载的功率由120 W变至240 W。 根据上述分析,可由负载功率在数值上的变化,进一步判断控制律中输出电流参数变量的变化情况。由于输入功率与输出功率具有相等的关系,在实际输出电压为恒压输出250 V的条件下,结合图11(a)和式(5)、(6),当系统输入功率为120 W时,实验样机由控制律计算得到的输出电流为0.48 A。在功率发生跳变时,同理结合式(5)、(6)以及图11(b)可知跳变后的输入功率值为240 W,由控制律计算得到的输出电流为0.96 A。因此,当系统负载功率发生变化时,其输出电压在保持恒压输出的情况下,可由此判断出控制律中的输出电流变量发生了相应变化。 (a) 输出电压波形图 (b) 输出电压纹波图 针对Boost PFC变换器在恒功率负载下的输出电流不连续性的问题,根据电路输出电压纹波的变化,判断出电路的功率变化情况,将二者相结合得到系统功率的预测函数,进一步由该函数计算得到连续的输出电流。仿真和实验结果证明,该控制律在电路负载为CPL的条件下,能够通过输出电压纹波快速精准判断负载功率的变化情况,计算出相应的连续型输出电流,从而实现整个系统的功率因数校正和恒压输出。2.2 非线性控制系统的坐标变换与控制器设计
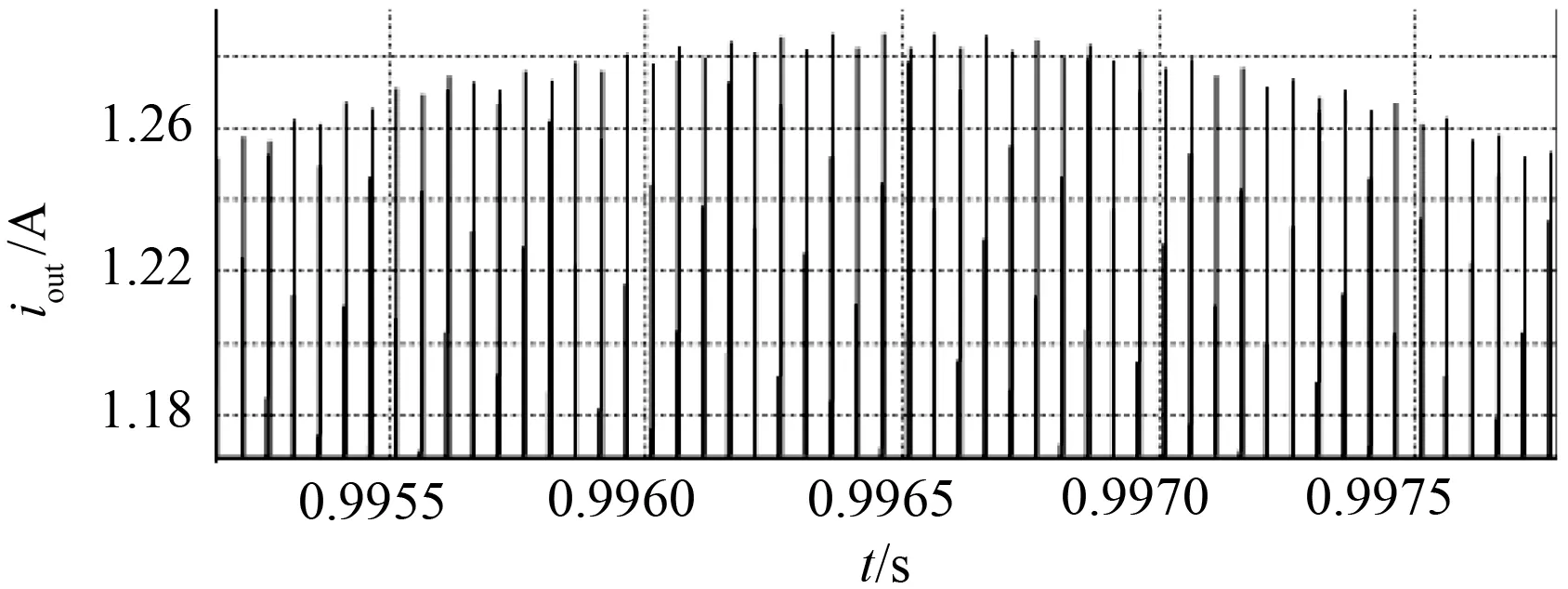

3 Boost PFC变换器带恒功率负载控制策略的改进



4 系统仿真与实验
4.1 系统仿真参数

4.2 期望输出电压为250 V条件下的仿真


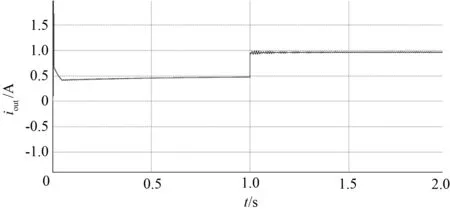
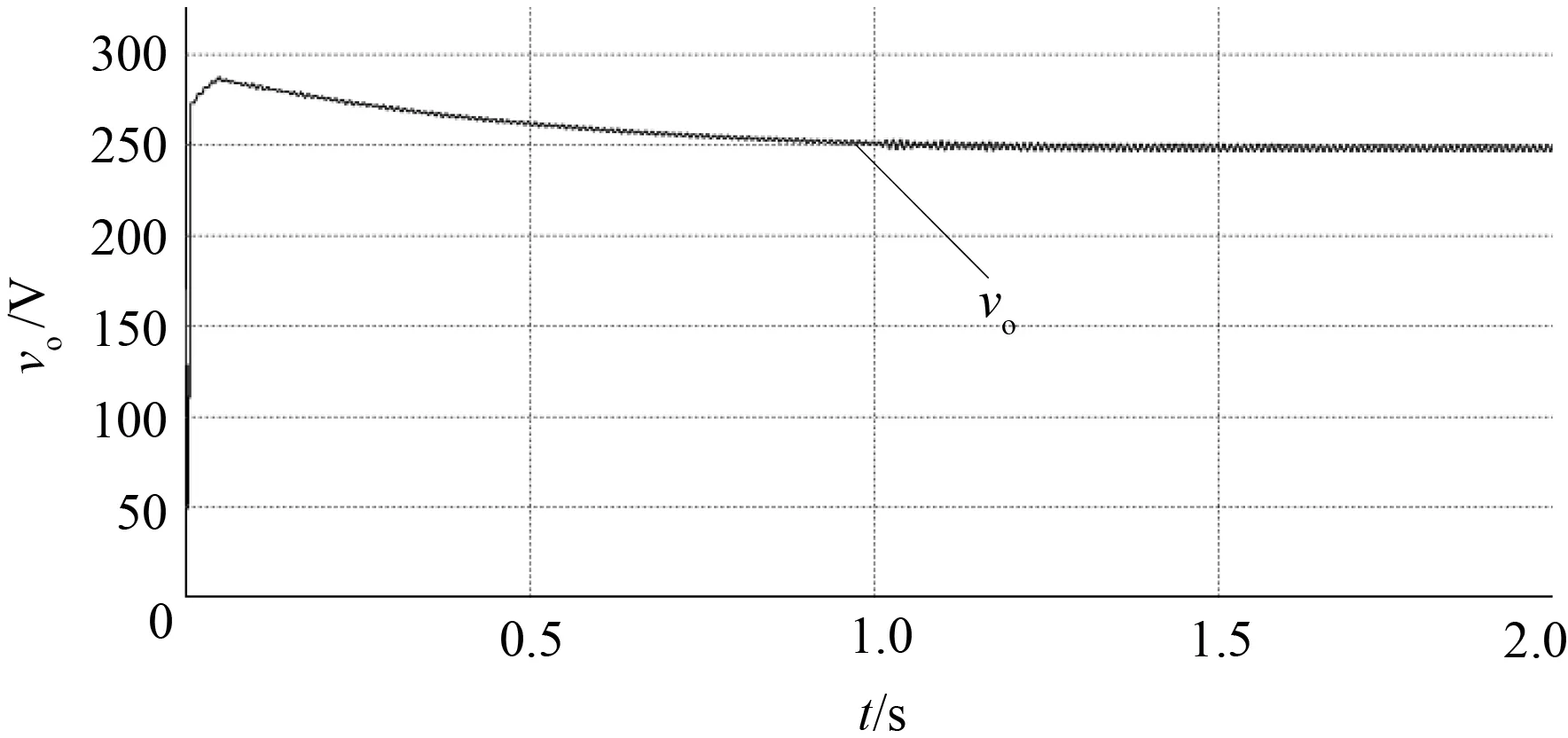


4.3 实验验证和结果分析




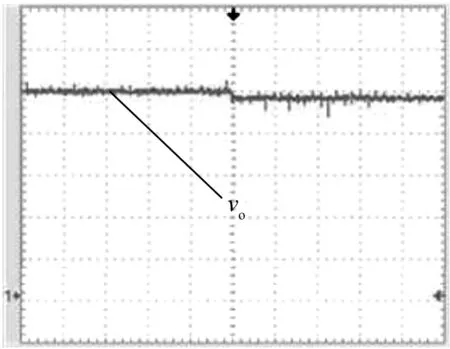
5 结论

