钢-混凝土预制混合梁受弯性能试验研究
张锡治 ,章少华,牛四欣,王湘安
(1. 天津大学建筑设计研究院,天津 300072;2. 滨海土木工程结构与安全教育部重点实验室(天津大学),天津 300072;3. 天津大学建筑工程学院,天津 300072)
在预制混凝土梁两端设置连接钢梁的预制混合构件,称为钢-混凝土预制混合梁,简称预制混合梁,其在提高施工效率、保证连接质量和缩短建造周期等方面有明显优势[1-2].目前对该类预制混合构件的基本力学性能已进行了相关研究,其中文献[3-4]利用ABAQUS有限元软件对采用栓钉和螺栓两种连接节点形式的预制混合梁进行了数值模拟,指出两种连接节点形式均可有效传递混凝土梁与钢梁间应力,栓钉和螺栓的数量及布置方式对构件整体受力性能影响较大.文献[5-6]对两端简支边界条件下预制混合梁的受弯性能进行了试验研究,认为钢梁和混凝土梁连接节点为刚性节点,试件具有较好的整体性能和延性.文献[7]进行了 2个预制混合梁试件在简支边界条件下的静力加载试验,结果表明,连接节点受力较小,在受力过程中基本处于弹性状态,破坏形态和承载能力与普通预制梁相似.文献[8]通过试验研究得到了预制混合梁的受剪破坏准则,指出钢与混凝土间黏结性能对受剪承载能力影响较大.
上述针对预制混合梁的研究多数集中于简支边界条件下的力学性能.由于目前工程中多采用刚性连接的梁柱节点,故开展预制混合梁在固支边界条件下的力学性能研究,分析钢与混凝土连接节点对预制混合梁整体受力性能的影响具有重要意义.本文通过 4个预制混合梁和 1个普通预制混凝土梁试件的受弯性能试验,探讨预制混合梁的破坏形态、承载能力、延性、变形性能和应变分布,研究本文提出的钢-混凝土连接节点的传力性能,考察不同参数对受弯性能的影响,并基于虚功原理建立预制混合梁极限荷载计算式.
1 预制混合梁组成
图 1给出了预制混合梁的组成以及钢与混凝土连接节点的具体构造.

图1 预制混合梁组成Fig.1 Composition of precast hybrid steel-concrete beam
预制混合梁由端部钢梁、连接节点和中部混凝土梁组成.上下连接板通过端板与 H型钢梁上下翼缘连接.为使混凝土梁纵筋应力直接传至钢梁翼缘,连接板与梁纵筋采用焊接连接.此外,在端板中部设置栓钉来传递端板与混凝土交界面处剪力.连接节点处箍筋由穿过连接板预留孔的2个U型箍筋焊接而成,以增强连接节点范围内混凝土与连接板的黏结性能.另外,还可根据梁跨度大小确定是否在混凝土梁内布置预应力筋以减小挠度,降低造价.
2 试验概况
2.1 试件设计
试件尺寸及配筋如图 2所示.共设计 5个预制梁试件,包括 4个预制混合梁试件 PHSC1~PHSC4和1个普通预制混凝土梁对比试件PC1,各试件的梁净跨 Ln均为 3600mm(梁净跨定义为预制梁两端固支端之间的距离,对预制混合梁,其净跨即为预制混合梁的总长度(包括端部钢梁),如图 2所示).预制混合梁与普通预制混凝土梁试件具有相同的混凝土梁截面,宽度 300mm,高度 400mm.试件 PHSC1~PHSC4的连接节点构造和钢梁截面尺寸均相同,端板厚10mm,宽度和高度分别为300mm和400mm;连接板厚 10mm,宽度 300mm,长度 130mm;端板中部栓钉直径16mm,长度 90mm,间距 100mm,共6个.各试件箍筋直径 10mm,间距 100mm,加载点与连接节点处箍筋间距 50mm.试件 PHSC1~PHSC4中纵筋与连接板的焊缝长度为 100mm,焊接方式为双面焊.对预制混合梁,制作时其端部钢梁部分埋入刚性块体内,以确保梁端固支边界条件的实现,如图 2所示.为与普通预制混凝土梁试件比较,试件PC1梁端截面设计受弯承载力与试件PHSC1~PHSC4梁端钢梁设计受弯承载力相同.试验参数包括钢梁长度 Ls、混凝土梁与钢梁受弯承载力比Muc/Mus以及混凝土梁与钢梁线刚度比ic/is,具体参数变化见表1.

图2 试件尺寸及构造Fig.2 Dimensions and details of specimens

表1 试件参数Tab.1 Parameters of specimens
2.2 材料力学性能
试件中钢材采用 Q345钢,纵筋和箍筋采用HRB400级钢筋,实测钢材力学性能指标(伸长率 δ、屈服强度 fy和抗拉强度 fu)见表 2.混凝土强度等级C40,实测边长 150mm 的标准混凝土立方体抗压强度平均值为38.8MPa.

表2 钢材力学性能Tab.2 Mechanical properties of steel
2.3 加载方案
使用压梁和螺栓将试件端部刚性块体与地面固定,成为梁端固定支座.跨中集中荷载由 100t油压千斤顶施加.试验加载采用分级加载,每级荷载增量在开裂前为20kN,开裂后为30kN,屈服后改为位移控制模式,每级位移增量 10mm,当荷载降至峰值荷载的85%时,加载结束.试验加载装置见图3.
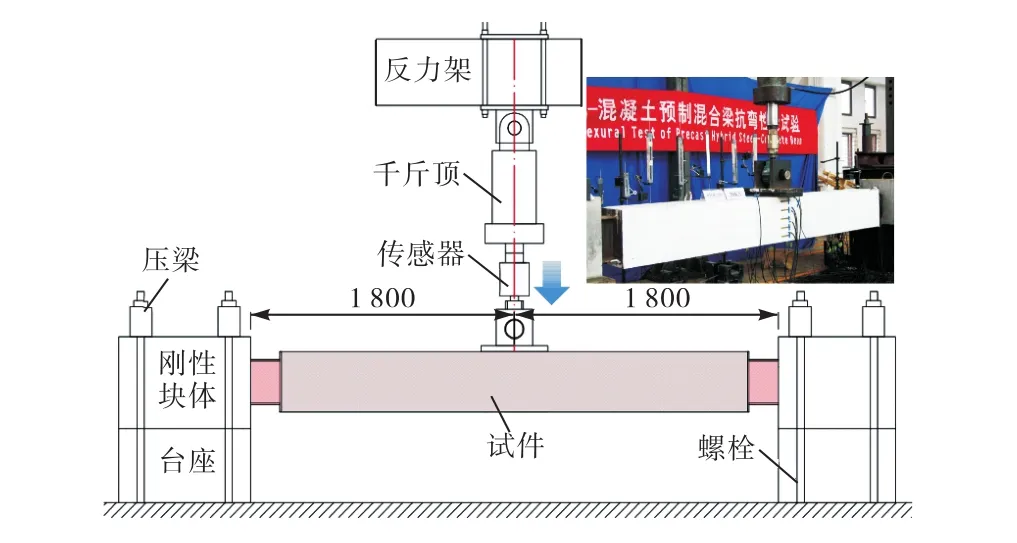
图3 加载装置Fig.3 Test setup
2.4 测点布置及量测内容
试件位移计布置见图 4,荷载-跨中挠度曲线由跨中加载点处荷载传感器和位移计测量.沿梁长度方向布置 7个位移计(D1~D7),用以测量试件挠度变形曲线;在梁两端刚性块体的侧面和顶面布置百分表(B1~B6),用以测量刚性块体的水平位移和转动.量测结果表明,试验过程中刚性块体水平位移和转动较小,可视为试件的固定支座.在钢梁上下翼缘和腹板布置应变片,用以测量钢梁应变;在连接节点的端板、栓钉以及与纵筋应变片对应的连接板位置布置应变片,用以测量端板、栓钉和连接板应变,验证焊缝连接方式在传力中是否可靠;在连接节点区域的纵筋、箍筋以及混凝土梁内纵筋布置应变片测量钢筋应变;在跨中截面沿梁高布置应变片测量混凝土应变,用于分析跨中截面应变沿梁高分布规律.图 5给 出了试件PHSC2的应变片布置.

图4 位移计布置Fig.4 Layout of displacement transducers

图5 试件PHSC2应变片布置Fig.5 Layout of strain gauges of PHSC2
3 试验现象及破坏形态
为确定加载过程中混凝土裂缝开展位置和宽度,试验前对混凝土部分进行刷白处理,并绘制100mm×100mm 网格.以下对各试件试验过程和破坏特征进行描述.
试件 PC1为普通预制混凝土梁试件.荷载达到90kN时,梁跨中受拉区出现第一条弯曲裂缝,梁端距支座 250mm处在加载至 100kN时出现弯曲裂缝;继续加载,梁支座及跨中不断出现新裂缝,已有裂缝继续开展并向受压区域延伸;加载至0.45Pm(Pm为峰值荷载),梁支座及跨中弯曲裂缝开始斜向开展;加载至 0.92Pm时,试件屈服,荷载-跨中挠度曲线出现拐点,此时支座和跨中区域裂缝已开展至0.75~0.90倍梁高处.随着加载继续,试件裂缝宽度和挠度均迅速增大.峰值荷载时,梁支座和跨中均已形成 2~3条主裂缝,最大宽度约为 3.4mm,受压区混凝土有压碎剥落现象.荷载在峰值点后开始缓慢降低,受压区混凝土压碎明显,试件最终破坏形态见图 6(a).
4个预制混合梁试件的破坏过程和试验现象基本相似,可分为以下4个阶段.
(1) 初始开裂阶段:随着荷载增加,试件 PHSC1和 PHSC2分别于 60kN和 65kN时在距端板约150~200mm区域内出现第一条受弯裂缝,随后分别于95kN和80kN时在跨中受拉区出现弯曲裂缝.试件PHSC3和PHSC4分别于80kN和85kN时在跨中受拉区出现第一条受弯裂缝,随后分别于95kN和90kN时在距端板约 150~200mm 区域内出现受弯裂缝.增加端部钢梁长度可延缓支座处混凝土梁端裂缝的出现.
(2) 斜裂缝形成阶段:继续加载,跨中受拉区域不断出现新裂缝,已有裂缝不断延伸和变宽,而梁端区域裂缝开展较为缓慢;加载至 0.35~0.45Pm,跨中区域弯曲裂缝大约在0.25~0.38倍梁高处斜向开展,形成腹剪斜裂缝,此时梁端裂缝以弯曲裂缝为主,斜裂缝较少.试件屈服时,跨中区域裂缝开展至 0.75~0.95倍梁高处,梁端裂缝开展至 0.25~0.75倍梁高处,端部钢梁越长,梁端裂缝开展高度越低.
(3) 峰值荷载阶段:试件屈服后,跨中挠度和裂缝宽度迅速增大,梁端原有裂缝继续开展,同时有新裂缝出现;峰值荷载时,各试件跨中受压区混凝土轻微压碎,除试件 PHSC1外,其余试件钢梁下翼缘均出现轻微屈曲现象.
(4) 破坏阶段:峰值荷载后,荷载开始缓慢下降,至试件破坏时,试件 PHSC1主要在跨中和与连接节点相邻的混凝土梁内形成塑性铰,端部钢梁保持完好;试件 PHSC2~PHSC4的塑性铰主要出现在端部钢梁和跨中混凝土梁内,端部钢梁腹板和下翼缘发生屈曲.
预制混合梁试件的最终破坏形态如图 6(b)~6(e)所示.由图 6可知,试件均发生弯曲破坏.普通预制混凝土梁破坏时,塑性铰主要出现在跨中和梁端;预制混合梁破坏时,除试件 PHSC1在跨中和与连接节点相邻的混凝土梁内出现塑性铰外,其余试件塑性铰均出现在跨中和梁端.
以上试验现象表明,预制混合梁内力传递路径清晰,受力明确.试件在连接节点相邻区域出现裂缝,连接节点区域裂缝较少;在加载过程中,连接节点始终保持较好的整体性,能有效传递钢梁和混凝土梁之间的应力.

图6 试件破坏形态Fig.6 Failure modes of specimens
4 试验结果及分析
4.1 荷载-跨中挠度曲线
各试件荷载-跨中挠度曲线如图 7所示,表 3给出了各试件特征点处的荷载及变形.表3中Pcr为开裂荷载,Py和 Δy分别为屈服荷载和屈服位移,Pm为峰值荷载,Pm/Py为强屈比,Δu为极限位移,μ为延性系数,K0为初始刚度.

图7 荷载-跨中挠度曲线Fig.7 Load-mid-span deflection curves
由图 7和表 3可以得出以下结论:①各试件荷载-跨中挠度曲线在开裂前呈线性变化,试件处于弹性阶段,开裂后,曲线出现明显拐点,试件进入裂缝开展阶段,跨中挠度增长较快;②试件 PHSC1~PHSC4的初始刚度分别为试件 PC1初始刚度的67%、59%、58%和 86%,预制混合梁初始刚度小于普通预制混凝土梁;③与试件 PHSC1相比,试件PHSC2和 PHSC3的峰值荷载分别提高 8.1%和9.2%,表明端部钢梁长度的增加可提高承载力;④与试件 PHSC1和 PC1相比,试件 PHSC4的峰值荷载分别提高16.4% 和1.7%,极限位移分别提高55%和33%,表明预制混合梁受弯承载力比的增加能有效提高承载力和变形能力;⑤与试件 PC1相比,试件PHSC1~PHSC4的强屈比分别提高 3.7%、8.3%、11.9%和 14.7%,表明预制混合梁屈服后弹塑性变形能力要优于普通预制混凝土梁.

表3 试件主要阶段试验结果Tab.3 Test results of specimens at main stages
4.2 延性分析
采用延性系数来评价构件延性[9].延性系数 μ=Δu/Δy.极限位移Δu取荷载下降至峰值荷载85%时的位移,屈服位移 Δy采用文献[10]中方法确定,各试件延性系数见表 3.图 8给出了钢梁长度、线刚度比和受弯承载力比对试件延性的影响规律.
由表3和图8可知,延性系数随端部钢梁长度的增加呈线性增长关系.当钢梁长度由200mm分别增加至400mm和600mm时,其延性系数分别增大约5%和 8%,表明预制混合梁延性随端部钢梁长度的增加而增大.线刚度比对延性系数的影响规律与端部钢梁长度相似,延性系数随线刚度比的增加大致呈线性增长趋势.在端部钢梁长度相同情况下,受弯承载力比由0.65增加至0.93时,延性系数提高126%,说明受弯承载力比对预制混合梁延性性能影响显著,受弯承载力比接近于 1.0时更有利于整体变形能力的提高.与试件 PC1相比,试件 PHSC1~PHSC3的延性系数降低约36%,试件 PHSC4的延性系数提高约 53%,原因为基于实测材料性能指标计算出的试件PC1梁端截面实际受弯承载力大于试件PHSC1~PHSC3端部钢梁实际受弯承载力,梁端塑性转动能力有一定程度提高,故试件 PC1延性系数高于试件PHSC1~PHSC3;试件 PHSC4因跨中截面配筋率增加,截面承载力和塑性转动能力比试件 PC1有较大提高,故其延性系数高于试件 PC1.试件 PHSC1~PHSC4的延性系数介于6.8~16.2之间,满足受弯构件延性系数不小于 3.0的要求[11],具有较好的延性性能.
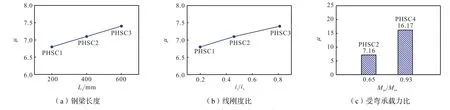
图8 各因素对延性的影响Fig.8 Effects of different factors on ductility
4.3 挠度曲线
图9为试件挠度曲线.由图9可知,各试件挠度在0.70Pm后有较快增长,试件PHSC1~PHSC4的增长幅度大于试件 PC1,峰值荷载时的挠度均比试件PC1大.在0.70Pm之前,预制混合梁试件的挠度曲线形状与普通预制混凝土梁试件相似,但在峰值荷载时差异较大.由于端部钢梁较强的变形能力,导致预制混合梁试件的裂缝主要集中于梁跨中受拉区域,梁端裂缝较少.因此,与预制混合梁试件相比,普通预制混凝土梁试件的挠度曲线更平滑.峰值荷载时,试件PHSC1~PHSC4跨中挠度分别达到梁净跨 Ln的1/52、1/56、1/60和1/52,试件的极限变形能力较好.
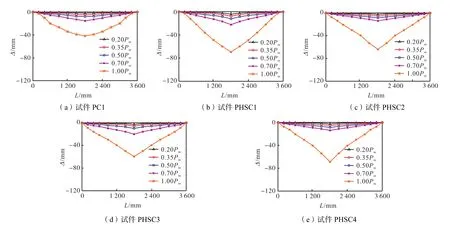
图9 试件挠度曲线Fig.9 Deflection curves of specimens
4.4 跨中截面应变分布
图 10给出了试件 PHSC1~PHSC4在各级荷载作用下跨中截面应变沿截面高度的分布和发展情况,图中横坐标以压应变为负,拉应变为正,h为应变测点到梁底的距离.分析图 10可发现,中和轴位置随荷载增大逐步向受压区移动,沿截面高度的应变分布基本呈线性,符合平截面假定的应变分布特征.
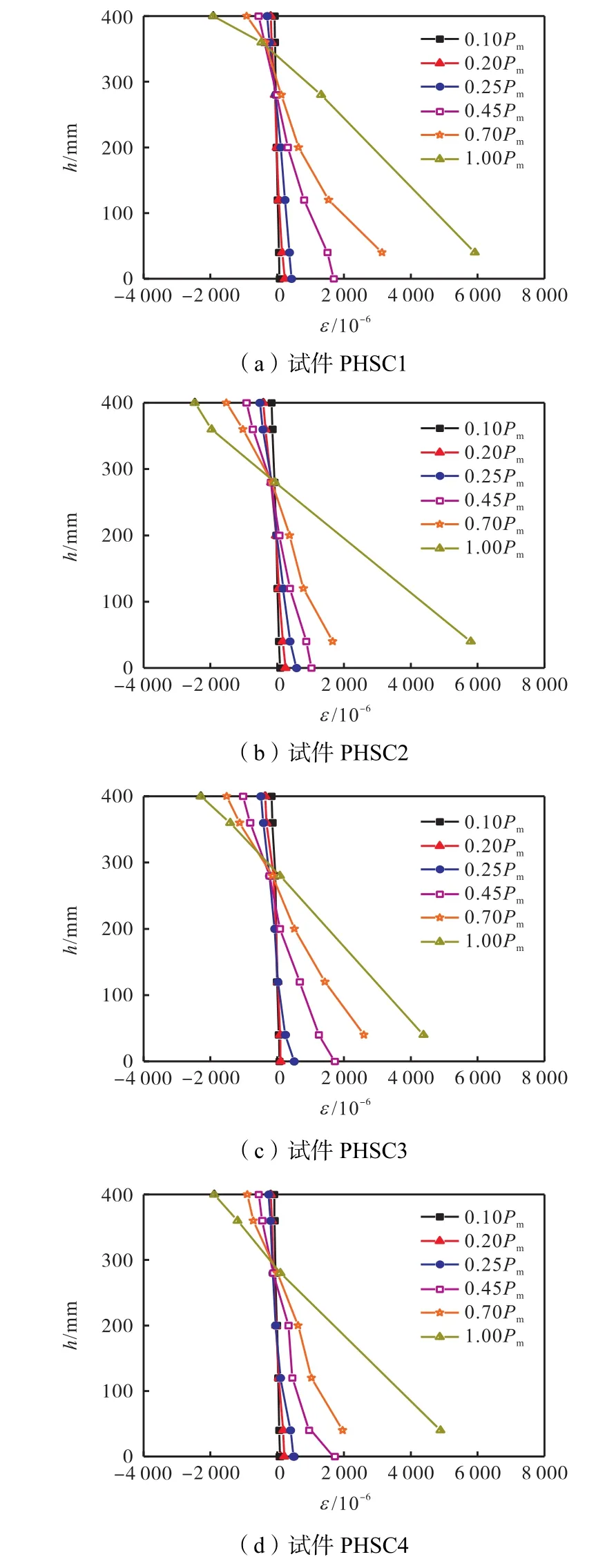
图10 跨中截面应变分布Fig.10 Strain distribution at mid-span section
4.5 钢梁及纵筋应变曲线
图 11为试件 PHSC1~PHSC4钢梁及纵筋的荷载-应变曲线,图中给出了各试件钢梁和纵筋应变测点位置.
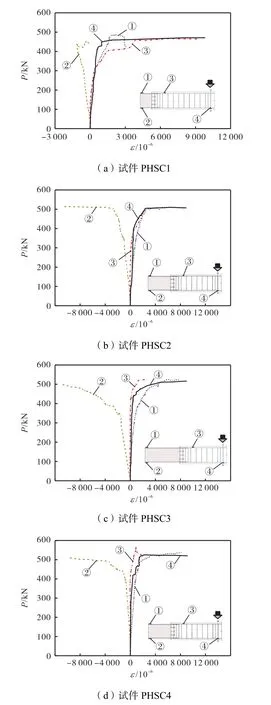
图11 钢梁及纵筋应变曲线Fig.11 Strain curves of steel and longitudinal bars
由图11可知,峰值荷载前,试件PHSC1端部钢梁翼缘应变随荷载的增加不断增大;峰值荷载后,钢梁上翼缘应变增长缓慢,钢梁下翼缘应变呈下降趋势,原因为梁端塑性发展逐步集中在混凝土梁端部,梁中内力出现重分布,导致钢梁应变降低,塑性发展不充分.由试验观测可知,钢梁未出现屈曲现象,梁端塑性铰位于与连接节点相邻的混凝土梁内.试件PHSC2~PHSC4中受拉纵筋和钢梁翼缘应变发展规律相似,连接节点相邻混凝土梁内顶部受拉纵筋的应变超过屈服应变,但由于峰值荷载后钢梁发生塑性变形,其应变增长缓慢;梁端塑性发展集中在钢梁内,说明试件整体变形能力较强.
4.6 沿梁长方向应变分布
通过设置在钢梁翼缘和纵筋的应变测点,可得到各级荷载下沿梁长方向的应变分布,如图 12所示,图中纵坐标为钢梁上翼缘或纵筋应变,应变均为拉应变,正负号分别代表顶面和底面位置,L为应变测点至左端支座的距离.
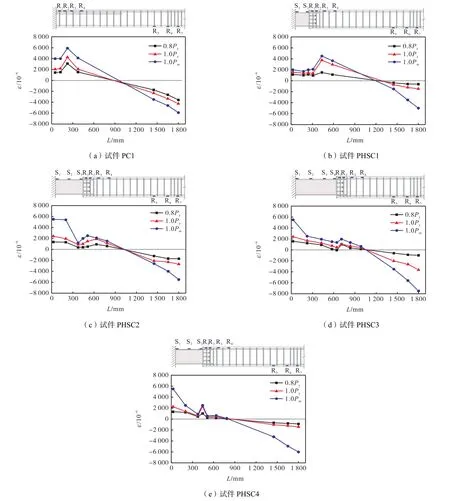
图12 沿梁长方向应变分布Fig.12 Strain distribution along beam length
由图12可知,在0.8倍和1.0倍屈服荷载以及峰值荷载下,各试件沿梁长方向应变分布与跨中集中荷载作用下两端固支梁弯矩图基本一致,说明预制混合梁整体性能较好,各部分间能协同工作.屈服荷载时,各试件沿梁长方向各测点应变值的连线与零应变水平线相交,其交点至纵坐标的距离:试件 PC1为880mm,试件 PHSC1~PHSC4分别为 1270mm、990mm、1040mm和870mm,其中试件PC1和试件PHSC4最接近理论弯矩图中反弯点到支座距离(900mm),表明提高受弯承载力比可增强预制混合梁的整体受力性能.峰值荷载时,试件 PHSC1~PHSC4连接节点处纵筋应变值均超过屈服应变1570×10-6,最大应变值 2300×10-6,表明连接节点能有效地传递钢梁和混凝土梁间应力.此外,连接节点处纵筋应变值随端部钢梁长度的增加呈减小趋势.
4.7 连接节点类型分析
作为预制混合梁的关键部位,钢梁与混凝土梁之间的连接节点应能可靠并有效地传递两者间应力,由于连接节点的转动变形降低了预制混合梁的整体性,因此,连接节点应满足刚性节点要求,以确保端部钢梁和中部混凝土梁形成整体受力构件.两端固支边界条件下预制混合梁的计算简图如图 13(a)所示.在跨中集中荷载作用下,连接节点假定为刚性节点和铰接节点时的弯矩图分别如图 13(b)和 13(c)所示.对试件PHSC1~PHSC4,在两种连接节点类型假定下,可分别得到屈服荷载 Py作用下的弯矩图以及钢梁段内任意位置处弯矩.基于弹性理论,可由钢梁截面处弯矩计算出钢梁翼缘的应变值[6].
为分析本文所提出的连接节点类型,对屈服荷载作用下试件 PHSC1~PHSC4钢梁上翼缘 S2测点(见图 12(b)~12(e)处的应变实测值和计算值进行比较,结果见表 4.由表 4可知,当连接节点假定为刚性节点时,各试件 S2测点处的应变计算值与试验值接近;当连接节点假定为铰接节点时,各试件的应变计算值与试验值相差较大,尤其是试件 PHSC1,其计算值与实测值的比值仅为 0.04.因此,本文所提出的连接节点可视为刚性节点,连接节点能有效传递钢梁和混凝土梁之间的应力.

图13 不同连接节点类型下梁弯矩图Fig.13 Bending moment diagrams of beams corresponding to different joint types
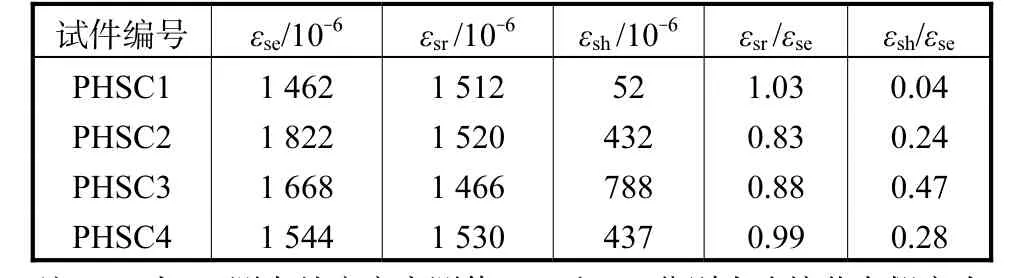
表4 各试件S2测点处应变实测值与计算值比较Tab.4 Comparison between measured and calculated values of strain on specimens at point S2
5 极限荷载计算
5.1 预制混合梁破坏机制
对两端固支边界条件下的单跨梁,当梁中形成 3个塑性铰时,结构处于极限状态,此时承担的外荷载即为极限荷载.通过确定塑性铰出现的位置及最终破坏机制,利用虚功原理可得到构件的极限荷载.

图14 预制混合梁破坏机制Fig.14 Failure mechanism of PHSC beam
试验结果表明,预制混合梁的破坏机制有 2种,第 1种破坏机制为连接节点相邻截面和跨中截面形成塑性铰,见图 14(a);第 2种破坏机制为梁端钢梁截面和跨中截面形成塑性铰,见图 14(b).在荷载作用下,构件出现塑性铰的位置与该处弯矩 M 和截面极限受弯承载力 Mu的比值有关,通常塑性铰首先出现在 M/Mu绝对值较大的截面[12].屈服荷载时,试件PHSC1~PHSC4梁端截面、连接节点相邻截面以及跨中截面的 M/Mu值列于表 5中.由表可知,对预制混合梁试件,通过 M/Mu值确定的塑性铰位置与试验结果一致.

表5 屈服荷载时各试件M/Mu值Tab.5 M/Mu values of specimens at yield load
5.2 基于虚功原理的极限荷载计算
根据各试件塑性铰出现位置和最终破坏机制,极限荷载可基于虚功原理得到[6].图 14为各试件最终破坏机制和塑性铰形成后机构发生虚位移的情况.对试件PHSC1(图14(a)),外力所做虚功为

式中:Pu为极限荷载;θ为塑性铰转角;L1和 L2为塑性铰至支座的距离.
体系所接受的变形虚功为

式中:Muc1和 Muc2分别为跨中混凝土梁截面和连接节点相邻混凝土梁截面的极限受弯承载力.
根据虚功原理We=Wi,可得
对试件PHSC2~PHSC4(图14(b)),外力所做虚功也为
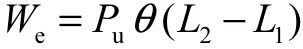
体系所接受的变形虚功为

式中Mus为梁端钢梁截面的极限受弯承载力.
根据虚功原理We=Wi,可得

根据式(3)和式(5)对各试件极限荷载进行计算,计算值与试验值的对比见表 6.表 6中 Pu,exp为极限荷载试验值,其值取试验得到的峰值荷载,Pu,cal为基于虚功原理的极限荷载计算值.由表 6可知,对试件PHSC1~PHSC4,基于虚功原理的极限荷载计算值与试验值吻合较好,计算值与试验值比值的平均值为1.00,变异系数为 0.04.因此,可利用虚功原理来预测两端固支边界条件下预制混合梁的极限荷载.
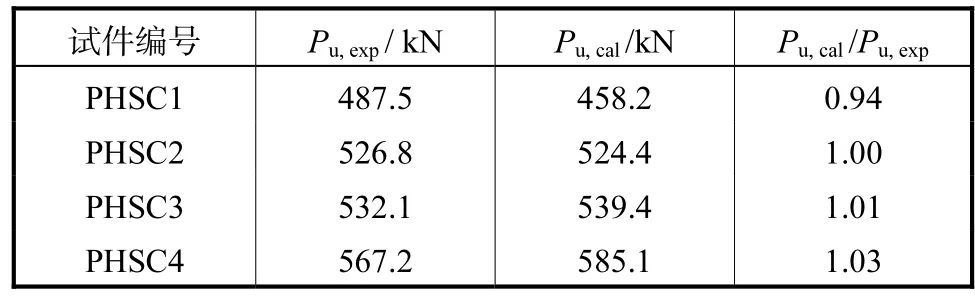
表6 极限荷载试验值与计算值比较Tab.6 Comparison between measured and calculated values of ultimate load
6 结 论
(1) 普通预制混凝土梁为梁端和跨中截面出现塑性铰的破坏机制.预制混合梁破坏机制有两种,一是梁端连接节点相邻混凝土梁截面和跨中混凝土梁截面形成塑性铰的破坏机制,端部钢梁无局部屈曲现象,保持完好;二是梁端钢梁截面和跨中混凝土梁截面形成塑性铰的破坏机制,端部钢梁出现屈曲破坏.
(2) 钢梁长度、受弯承载力比以及线刚度比的增加均可提高承载力和延性,其中增加受弯承载力比的效果更显著;与普通预制混凝土梁相比,预制混合梁的强屈比提高约 4%~15%,其屈服后弹塑性变形能力较好,更有利于耗能.
(3) 在受力过程中,钢-混凝土连接节点始终保持较好的整体性,未出现严重破坏;基于连接节点假定为刚性节点的应变分析结果与试验结果相吻合,连接节点可视为刚性节点,预制混合梁中不同部分之间的应力可通过连接节点可靠传递.
(4) 预制混合梁初始刚度比普通预制混凝土梁小;在同级荷载下,预制混合梁跨中挠度大于普通预制混凝土梁;峰值荷载时,试件 PHSC1~PHSC4的跨中挠度分别为梁净跨 Ln的 1/52、1/56、1/60和 1/52,预制混合梁极限变形能力较好.
(5) 端部钢梁较强的变形能力导致预制混合梁裂缝集中在跨中受拉区,而梁端裂缝较少,其挠度曲线在 0.7倍峰值荷载后与普通预制混凝土梁相差较大;预制混合梁跨中受拉区裂缝宽度和开展范围均大于普通预制混凝土梁.
(6) 基于虚功原理建立了预制混合梁的极限荷载计算式,计算值与试验结果吻合较好.

