基于EEMD-小波阈值去噪的桥梁结构模态参数识别
熊春宝,于丽娜,常翔宇
(1. 天津大学建筑工程学院,天津300072;2. 天津市交通科学研究院,天津 300074)
结构振型、自振频率和阻尼比是反映桥梁动力特性和安全的重要模态参数.然而,桥梁在长期使用过程中,由于材料老化、环境侵蚀以及车辆荷载等诸多因素影响,不可避免地出现结构损伤和性能退化,使其刚度降低,进而引起模态参数发生变化,严重影响着桥梁结构安全[1-3].基于环境激励的结构动态变形监测和模态参数识别,能够避免因外部激励过大而对结构造成不必要损伤,同时避免因外部激励与环境激励耦合作用而影响模态识别精度,目前被广泛应用[4-6]. 结构模态参数识别主要分为时域识别和频域识别,其中时域方法对输入激励无要求,只需利用实测响应信号即可提取结构动力参数,更适于环境激励下的结构模态参数识别[7].RDT和 ITD 法是较为常用的时域识别方法,两者结合可实现结构自由衰减信号提取和模态参数识别.受周围环境影响,监测的结构振动信号中难免包含噪声[8].因此,信号降噪处理是结构动力特性分析和模态参数识别前的关键步骤,直接关系到分析结果的准确性.
经验模态分解(empirical mode decomposition,EMD)[9]和小波分解[10]是目前常用的信号降噪方法,二者对非线性非平稳信号具有较好的适用性.其中,小波分解需要预先确定基函数和分解尺度,EMD方法则可依据信号局部特征信息实现多分辨率分析.然而,EMD算法本身缺陷导致固有模态函数(intrinsic mode function,IMF)分量存在端点效应和模态混叠问题.总体经验模态分解(ensemble empirical mode decomposition,EEMD)[11]是在EMD算法基础上,通过多次掺入白噪声填充整个时频空间,使端点极值分布均匀化,从而具有更高的频率分辨率.EEMD虽然改善了端点效应和模态混叠,但仅经过有限次数的集成平均,重构信号中依然存有残余白噪声,导致对有效 IMF分量的判定和筛选缺乏明确的依据.小波阈值去噪是在小波分解的基础上,根据信号特性自适应选择相应频带来匹配信号频谱,对白噪声具有较强的抑制能力.然而,小波阈值去噪对高信噪比信号较为有效,当信噪比较低时,在噪声主导的区域,小波基的搜索只是为了描述噪声,反而不利于去噪[12].
针对上述采用单一方法滤波降噪的不足,人们开始着手研究 EMD相关方法与小波阈值去噪的联合应用:李琳等[13]针对低信噪比转子振动信号处理中的噪声问题,提出了改进 EMD和小波分析相结合的去噪方法;练继建等[14-15]以及张建伟等[16]在泄流泄洪结构实测信号分析中,逐步改进了 EMD相关方法,并用其与小波阈值联合降噪;徐朗等[17]针对大坝监测数据,提出 CEEMDAN与小波变换相结合的降噪方法;王红君等[18]在风电齿轮箱故障诊断分析中,采用 EEMD分解和小波阈值相结合方法对信号进行预处理.研究结果表明,采用小波阈值去噪方法进行二次降噪,能够有效抑制高频白噪声,使联合降噪方法优于应用单一方法.在EMD算法基础上,EEMD、CEEMD、CEEMDAN等改进算法能够改善端点效应和模态混叠,然而,关于EMD分解后有效IMF分量的判定值得进一步研究.
本文针对环境激励下桥梁结构动态变形监测信号的噪声问题,提出改进 EEMD-小波阈值联合去噪方法,利用平均周期图法和相关系数法双重判定准则剔除虚假 IMF分量.首先,采用 EEMD算法对监测信号进行分解,通过双重判定原则筛选重构 IMF分量.然后,针对 EEMD分解重构后的残余白噪声,采用小波阈值去噪方法对重构信号进行二次降噪.通过仿真信号验证 EEMD-小波阈值去噪算法的效果,再将此组合方法应用于天津永和桥竖向振动信号处理,采用RDT-ITD法进行结构模态参数识别,并与有限元分析结果进行比较.
1 EEMD-小波阈值去噪算法
1.1 EEMD算法
EEMD算法是在原始信号中多次加入高斯白噪声,然后进行 EMD分解,再将多次分解得到的 IMF分量进行总体平均运算.参考文献[9,11],EEMD 算法的数学表达式为
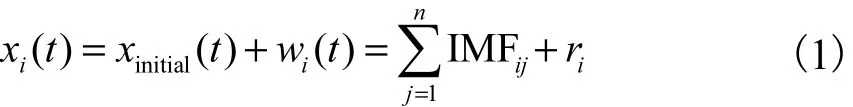
式中:wi(t)为第 i次加入的白噪声;xi(t)为第i次加入白噪声后的信号;ri为第i次分解产生的余项;n为EEMD分解所得IMF数目.

式中m为总体平均次数.
真实的 IMF分量与原信号具有很好的相关性,而由于端点震荡引起的虚假 IMF分量与原信号的相关性很差[19-20].因此,可通过相关系数来判定虚假分量,去伪存真,完成 EEMD的信号重构.相关系数的数学表达式为

式中:X为各 IMF分量;Y为原始信号;N为信号数据长度.
此外,通过功率谱密度(power spectral density,PSD)峰值,能够直观判断 IMF分量信号的纯净程度和结构固有频率值.平均周期图法是计算功率谱密度函数的基本方法,其原理是将随机振动信号的数据进行 Fourier变换以进行功率谱密度估计,其数学表达式为
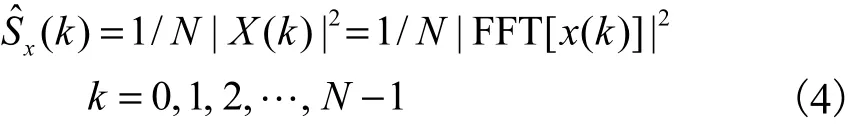
式中:x(k)为离散信号数据;F F T[x (k)]代表对数据x(k)进行Fourier变换.
本文综合考虑两种计算结果,筛选出相关系数较大且功率谱密度峰值较为明显的 IMF分量进行重构,作为EEMD滤波后的信号数据.
1.2 小波阈值去噪
信号经小波阈值去噪二次处理时,既要消除残余白噪声表现出的高频分量,又要保留那些反映信号突变的高频分量[10].小波包分解能同时对信号的高频和低频部分进行分解,具有更好的分辨率.小波包分解算法的数学表达式为
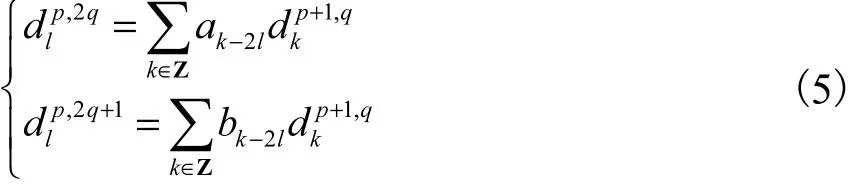
重构算法的数学表达式为
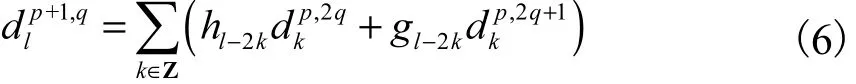
式中hl-2k和gl-2k是一组正交共轭系数.
小波阈值处理方法主要分为硬阈值和软阈值,其中硬阈值能够较好保留信号局部特征,但是其不连续性会导致消噪后阈值附近噪声明显.为防止信号失真,本文选取硬阈值方法,其数学表达式为
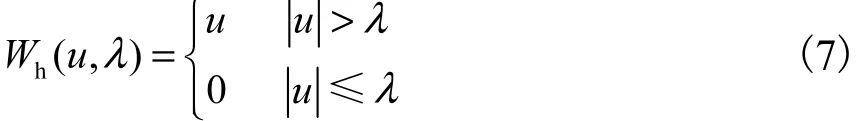
式中:u为变量;λ为阈值.
本文选用斯坦恩无偏估计作为阈值准则,参考文献[21],阈值λ设为

2 EEMD-小波阈值去噪与模态识别
本文采用RDT-ITD法进行模态参数识别,假定环境激励为白噪声,进而利用平稳随机振动信号的性质分离受迫信号和随机信号,以获取结构的自由衰减振动响应信号,再对结构模态参数进行识别.在进行模态参数识别前,先根据上述联合降噪方法对信号进行降噪处理,信号降噪和模态识别具体流程如下:①对测量信号进行EEMD分解,得到一组IMF分量;②计算IMF分量与原信号的相关系数及IMF分量的功率谱密度;③根据②判断选取信号的主导模态分量,进行信号重构;④对重组信号进行小波阈值去噪,得到最终降噪后的信号;⑤截取一定长度的信号时程,利用 RDT法提取结构自由衰减响应,并基于峰值拾取法拟合衰减趋势;⑥针对RDT结果进行3次不同延时的采样,构造自由衰减响应数据矩阵;⑦采用 ITD法求解结构模态参数.算法流程如图1所示.
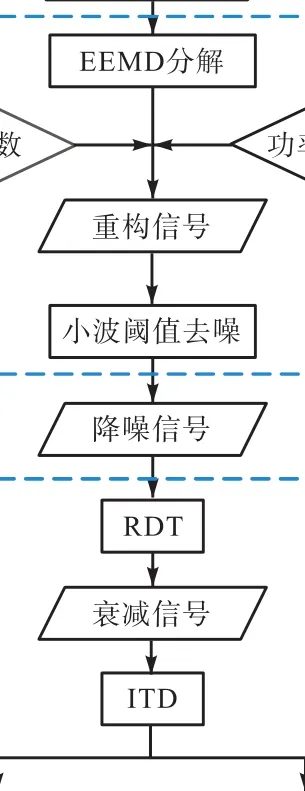
图1 信号去噪与模态参数识别流程Fig.1 Signal denoising and modal parameter identification process
利用数字仿真信号验证联合滤波方法的有效性,其数学表达式为

加噪后信号的数学表达式为

式中:w为白噪声分量;y2的信噪比为2.5407.
表 1为 3种不同方法的降噪效果指标.由表 1可知,采用EEMD方法时信号降噪效果提升较小,这是由于在重构信号时选取了前几阶相关系数较高,但含有较多高频噪声的IMF分量;采用EEMD-小波阈值方法对信号进行处理,信号信噪比最高,均方根误差最小,与原始仿真信号相关性最高,证明了联合降噪方法的有效性.
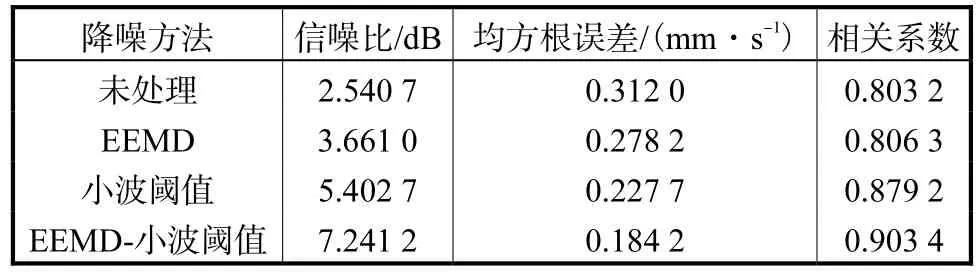
表1 不同降噪方法的效果指标Tab.1 Denoising effect indices of different denoising methods
3 桥梁结构模态参数识别应用
3.1 工程概况
永和桥位于天津市东郊,是一座双塔双索面的预应力混凝土斜拉桥,全长510m,跨径组成为25.15m+99.85m+260m+99.85m+25.15m.本次试验选择941B拾振器,采用大速度档位,灵敏度0.8 V·s/m,量程0~0.6m/s.拾振器采样频率为25Hz,单点采样时间 30min.为了分析桥梁在环境激励下的动力响应,试验过程中交通封闭,结构仅受地脉动和风荷载作用.在桥面及塔顶布置测点进行监测,其中塔顶布置水平传感器,桥面布置竖向传感器.竖向传感器布置按照跨径划分:主跨布置在 8分点位置处,次跨布置在4分点处,边跨布置在跨中,整体布置如图2所示.选择主跨跨中监测点数据进行分析,截取 1000s时长,共计 25000个数据点.信号时程曲线如图 3所示.

图2 桥梁结构整体布置示意(单位:m)Fig.2 Overall layoutof the bridge structure(unit:m)
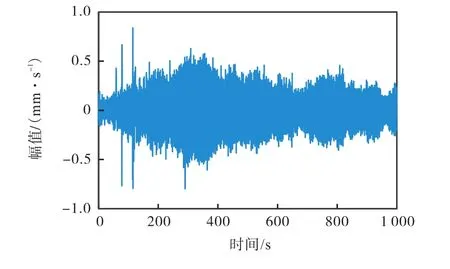
图3 桥梁跨中点振动响应时程信号Fig.3 Time history signal of the bridge vibration response at the midpoint of bridge span
3.2 有限元模拟
建立桥梁结构有限元模型,模拟桥梁上部结构动态响应,获取桥梁结构自振频率参数,并与实测信号识别结果进行对比分析.全桥主梁、主塔、承台采用梁单元模型;索单元采用桁架单元,每个断面 4根拉索,同侧两根拉索按面积等效为单根拉索;辅助墩拉力摆采用只受拉桁架单元模拟.全桥实际为纵向漂浮体系,在跨中添加纵向约束.
有限元模拟得出的结构前 3阶竖向自振频率分别为 0.3911Hz、0.8878Hz、1.2475Hz,对应振型如图4所示.

图4 结构前3阶竖向模态振型Fig.4 Vertical mode shapes of the first three orders
3.3 滤波降噪处理
3.3.1 添加白噪声标准差和集成次数确定
首先确定 EEMD分解所需添加白噪声标准差和集成次数,参考文献[22],重构信号误差标准差e取值为0.02,计算求得原始信号幅值标准差0σ=0.1893,高频成分幅值标准差hσ=0.1877,添加白噪声幅值标准差取值范围为

取nσ=0.05,集成平均次数为

本文T取值为175.
3.3.2 虚假分量判定与信号重构
经EEMD分解得出的14个IMF分量如图5所示.各 IMF分量与原始信号的相关系数,如表 2所示.参考文献[23],相关系数阈值为0.092.IMF1~6均大于阈值,满足要求.
前6阶IMF分量的功率谱密度频谱函数如图6所示.由有限元模拟可知,结构的前 3阶自振频率最大为 1.2475Hz,因此图 6中只给出频域 0~2Hz部分,其中,IMF分量 2~5包含了振动频率的主要信息.IMF1分量各频率处功率分布无明显峰值,接近白噪声特性;IMF6分量在 0.4Hz处显示出明显峰值,但是在频率大于 0.7Hz后,功率谱能量很低.两分量虽然包含一定原始信息,但与原始信号相关系数较小,对重构信号峰值识别影响不大,故舍弃 IMF1和IMF6,选取IMF2~5作为EEMD分解重构信号.

表2 各IMF 与原信号的相关系数Tab.2 Correlation coefficient values between IMF and original signal
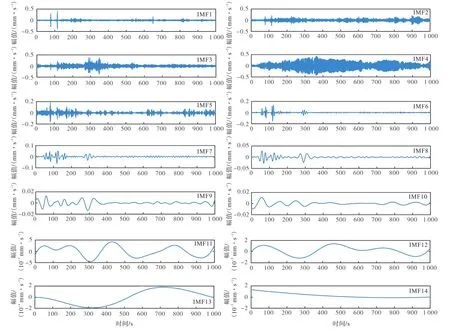
图5 EEMD分解结果Fig.5 Results of EEMD decomposition
3.3.3 小波阈值去噪
针对 EEMD分解重构信号的残余白噪声,采用小波阈值方法进行进一步降噪.本文采用斯坦恩无偏风险估计作为阈值选择准则,选择 db2小波类型,进行 3层分解,数据长度为 24992,阈值取为5.0612.小波阈值去噪前后信号对比如图 7所示,滤波后信号幅值明显减小.滤波后功率谱密度函数如图 8所示,从中可直接识别出结构振动基频,其余处峰值存在毛刺多、不光滑、模态密集现象,需要进一步处理.

图6 IMF1~6分量功率谱密度幅频曲线Fig.6 Power spectral density amplitude-frequency curves of IMF1—6
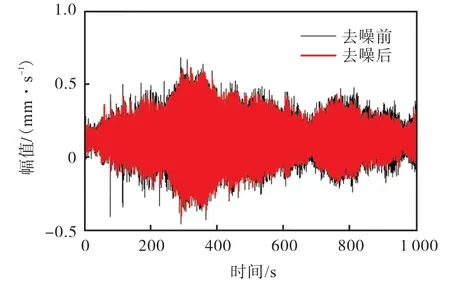
图7 小波阈值去噪前后时程信号对比Fig.7 Comparison of the signals before and after wavelet threshold denoizing
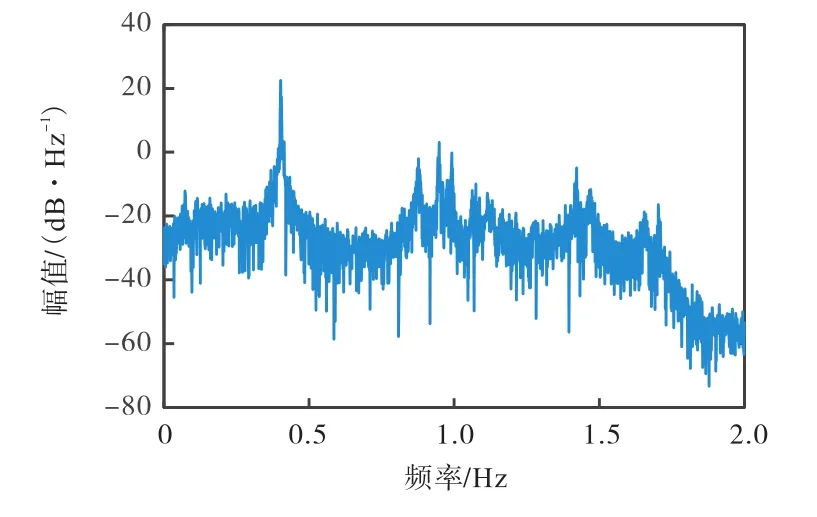
图8 滤波后功率谱密度幅频曲线Fig.8 Power spectral density amplitude-frequency curve after wavelet threshold denoizing
3.4 模态参数识别
从降噪后的信号中截取 250s时程数据,利用RDT法提取桥梁自由振动衰减响应,采用峰值拾取法拟合衰减趋势,结果如图 9所示.然后,利用 ITD法提取结构自振频率和阻尼比,经过判定筛选,剔除虚假模态值,提取出结构前 3阶固有频率和阻尼比值,如表3所示.表3还列出有限元模拟得到的结构固有频率和相对误差.本文所提方法与有限元模拟结果基本吻合,其中,结构振动基频的识别值与模拟值相对误差最小,仅为 3.07%.模态参数识别值均大于模拟值,说明桥梁经过一定时间的使用,结构动态响应特性发生变化.
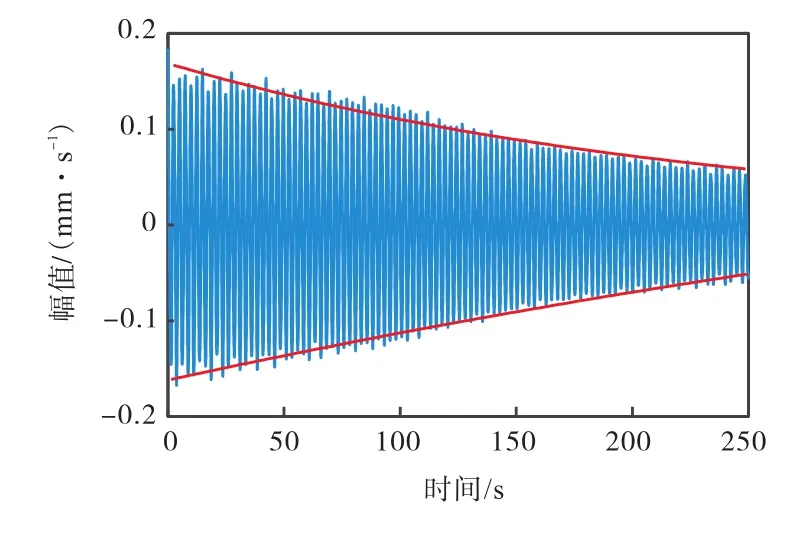
图9 RDT自由衰减信号Fig.9 Free decay signal of RDT
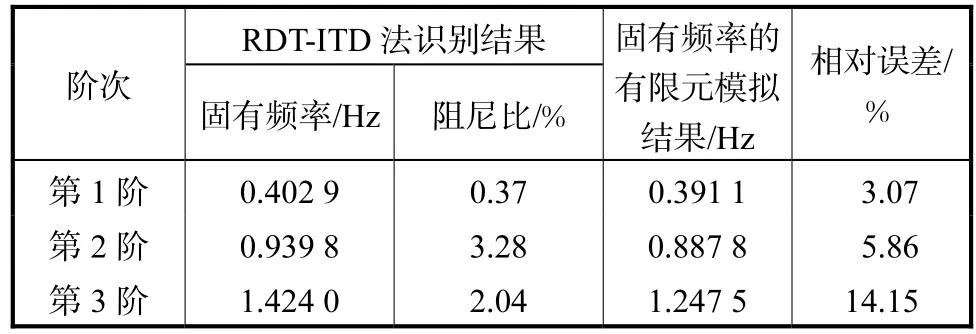
表3 RDT-ITD法模态参数识别与有限元模拟结果Tab.3 Modal parameters of RDT-ITD and FE simulation results
4 结 论
本文以某大跨径斜拉桥为对象,基于动态变形监测数据研究结构竖向振动响应特性,提出 EEMD-小波阈值联合滤波降噪方法,在数据降噪之后采用RDT-ITD法进行结构模态参数识别.将所提方法应用到桥梁模态参数识别中,与有限元模拟结果进行对比,得出以下结论.
(1) 采用 EEMD-小波阈值联合滤波降噪方法,通过相关系数和 IMF分量双重选择,选出有效 IMF分量再进行小波阈值去噪,能够最大限度消除残余噪声.仿真信号分析表明,相对于单一的 EEMD或小波阈值去噪方法,EEMD-小波阈值联合滤波降噪方法能更有效抑制监测信号中的噪声成分.
(2) 信号滤波降噪后,采用 RDT-ITD算法能够准确识别出结构前3阶竖向自振频率,与有限元分析结果基本一致,振动基频实测值与模拟值相差3.07%.
(3) 模态参数识别值均大于模拟值,说明桥梁经过一定时间的使用,结构动态响应特性发生变化.本次计算结果可为有限元模态更新提供参考.

