基于雅可比矩阵的连续型机器人灵活性分析
康荣杰,王 聪,耿仕能,杨铖浩,
(1. 天津大学机构理论与装备设计教育部重点实验室,天津 300350;2. 天津工业大学机械工程学院,天津 300387)
随着机器人学与仿生技术的快速发展,连续型机器人得到了越来越多的关注.连续型机器人采用与章鱼触角、象鼻等生物器官类似的结构,不具有刚性连杆,可以柔顺地改变自身形状以适应环境.由于连续型机器人这种独特的自身结构优势,目前已经广泛应用于医疗手术、空间操作、探测救援等领域[1].
目前,国内外有很多机构和学者针对连续型机器人的设计、建模、控制等方面展开了研究.其中,采用丝驱动与气压驱动作为连续型机器人控制输入的研究较多[2].文献[3-4]提出了Air-OCTOR以及OctArm等一系列连续型机器人,并对传统刚性机器人的D-H建模法进行改进,使其适用于连续型机器人的运动学分析.文献[5]开发了一种新型丝驱动连续型机器人,可以通过利用置于关节内的相变合金的热机械性来实现变刚度的效果.文献[6]提出了一种带有约束的丝驱动柔性机器人,通过主动控制弯曲关节的长度和曲率,可以实现增大工作空间等功能.Festo和BUAA合作开发了一种仿章鱼触手软体抓持器,其由柔软的硅胶结构组成,通过气压驱动可以实现连续灵活的大幅度柔顺变形[7].文献[8-10]也对丝驱动、气压驱动、混合驱动等多种类型连续型机器人展开了详细的研究,并基于运动学建模,进行了卡尔曼滤波控制、工作空间分析等相关工作.此外,随着智能材料与 3D打印技术的快速发展,一些学者开始将形状记忆合金等新型驱动形式应用于连续型机器人的控制中[2].文献[11]设计了一种采用 SMA 弹簧驱动的微创手术机器人,可以通过控制每个关节的弹簧伸缩实现不同程度的灵活弯曲.上述研究都提到了连续型机器人在操作灵活性方面存在优势,并在运动学模型、控制等方面做了深入的分析,但是却很少有针对连续型机器人运动灵活性开展的相关研究.
目前,对机器人运动灵活性进行分析常采用以下两类指标:一是基于服务区、服务球等指标[12]考察机器人末端在工作空间中的特定位置下所有姿态的集合;二是基于雅可比矩阵条件数、奇异值等指标[13]对机器人末端沿工作空间内任意方向的运动能力进行考察.Wu等[14]在Badescu等[12]对多关节刚性机械臂灵活性的研究基础上,基于服务区的概念,对连续型机器人的灵活性展开了分析.Gravagne等[15]将连续型机器人看成一种特殊的串联机器人,对其灵活性进行了运动学与力学可操作度方面的探究,但是该灵活性分析仅局限于平面内.Khadem 等[16]基于雅可比矩阵,提出了一系列的可操作度指标,对同心管连续型机器人展开了灵活性分析.然而,以上设计并没有将连续型机器人的灵活性与结构设计相结合,而用灵活性来指导结构设计是连续型机器人研究的重点之一.由于目前针对连续型机器人的建模与控制主要基于速度雅可比矩阵展开,且雅可比矩阵的性能直接影响机器人的操作性能,因此本文基于运动学模型与雅可比矩阵分析连续型机器人的灵活性.
本文对连续型机器人的灵活性进行了详细的分析,将灵活性与机器人的关节长度设计相结合,引入优化算法,利用灵活性来指导关节长度的分配,并揭示了基于雅可比矩阵条件数的灵活性指标与操作灵敏度的关联关系,为连续型机器人的结构设计与控制提供有力的支撑.
1 连续型机器人运动学分析
图 1所示为连续型机器人样机三维图.机器人本体分为 2个关节,靠近驱动箱的关节定义为关节1.每一个关节由中央脊椎丝、驱动丝和连接盘 3部分组成,3根驱动丝间隔 120°布置,穿过连接盘上的过孔并与关节末端连接盘相固联.关节 2的 3根驱动丝穿过关节1中连接盘的过孔,并与关节1中的驱动丝间隔 60°分布.其中,中央脊椎丝与驱动丝均为既可承受推力又可承受拉力的超弹镍钛合金丝,连接盘为3D树脂打印材料.由于中央脊椎丝起支撑固定作用,且整体的长度不发生改变,因此通过控制关节中驱动丝长度的变化,就可以实现机器人不同构型的弯曲.另外,机器人采用模块化设计,通过调整每一关节连接盘的间距与数量,便可以实现关节长度的灵活改变.
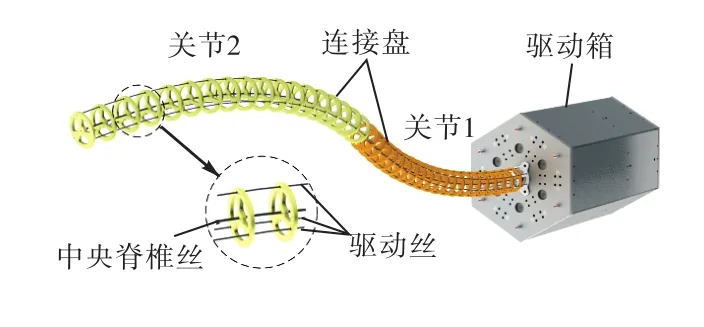
图1 连续型机器人样机Fig.1 Prototype of a continuum robot
1.1 建模相关参数和定义
假设连续型机器人运动时各个关节均为等曲率弯曲[17],且每一关节都由均匀分布的3根丝驱动.在关节 i (i = 1 ,2,… ,n )的初始连接盘与末端连接盘上分别建立该关节的基座坐标系 Oib( xib, yib, zib)与末端坐标系 Oie( xie, yie, zie),如图 2(以关节 1为例)所示.其中,规定关节1的基座坐标系为整个机器人的基座坐标系.则可通过以下 3个空间来描述机器人的运动学模型:驱动空间 Q = [ li,j]T(i = 1 ,2,… ,n; j =1,2,3)用于 反 映 驱 动 丝 长 度 变 化 ;构 型 空 间 Ψ =[θi,δi]T(i = 1 ,2,… ,n )用于描述连续型机器人弯曲形状;工作空间 P =[x,y,z]T用于描述机器人末端点位置.其中,定义 Li(i = 1 ,2)为第 i个关节中央脊椎丝的长度,li,j(i = 1,2,… ,n; j =1,2,3)为第 i个关节中第 j根驱动丝的长度.θi( i = 1 ,2,… ,n )为第 i个关节的弯曲圆心角,即第i个关节弯曲后末端连接盘与初始连接盘所形成的夹角.δi(i = 1 ,2,… ,n )为第i个关节的弯曲方向角,即第i个关节最大弯曲所在平面与该关节基座坐标系中xibzib平面的夹角.
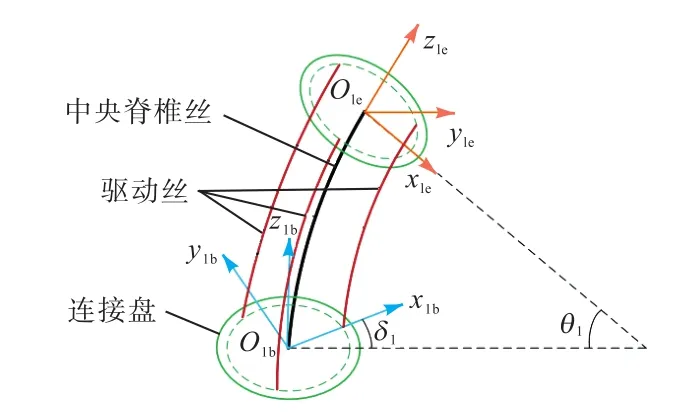
图2 关节1的建模参数Fig.2 Modeling parameters of joint 1
1.2 单关节运动学模型
基于上述运动学建模相关假设和定义,仅仅考虑每个关节自身,连续型机器人第i个关节驱动空间Q、构型空间Ψ和工作空间P之间的关系可以表示为

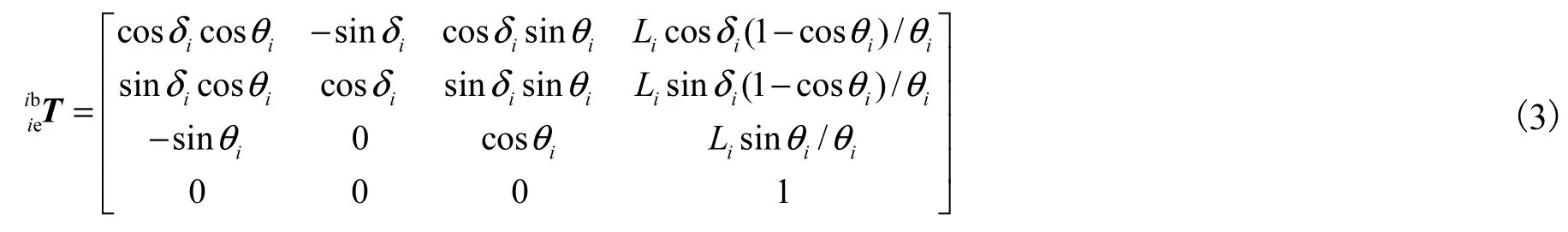
式中:α=120°,为第i个关节3根驱动丝之间的分布角度;Pie与Pib分别为第 i个关节末端坐标系和基座坐标系的位置坐标.
1.3 多关节运动学模型
将单关节运动学模型中驱动空间Q、构型空间Ψ与工作空间 P之间的关系拓展到多关节,便可以得到多关节之间的运动学模型.但是,要注意的是,考虑多关节驱动空间Q与构型空间Ψ之间的关系时,由于第 i (i ≥ 2 )个关节的驱动丝要穿过第 1至第i-1个关节,因此需要考虑运动学的耦合问题;且考虑多关节构型空间 Ψ与工作空间 P之间的关系时,由于第i (i≥2)个关节的基座坐标系Oib与第i-1个关节的末端坐标系 O(i-1)e并不重合,因此需要考虑两坐标系之间存在的旋转角度.故综合考虑上述因素,连续型机器人第i (i≥2)个关节驱动空间 Q、构型空间Ψ、工作空间P之间的关系可以表示为
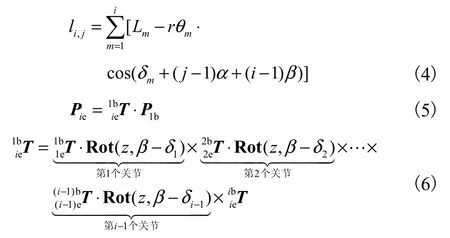
式中:i= 1,2,… ,n; j =1,2,3;r为驱动丝所在的分布圆半径,在本文中取 r = 1 5mm ;β为第i (i≥2)个关节与第i-1个关节驱动丝之间的夹角,故β= 2 π /(3i),如图3所示.

图3 两关节连续型机器人驱动丝分布情况示意Fig.3 Distribution of driving cables in a two-joint continuum robot
1.4 雅可比矩阵与工作空间
速度雅可比矩阵反映了连续型机器人关节驱动空间 Q、构型空间 Ψ、工作空间 P之间的速度关系,是后续对机器人进行灵活性分析、运动学仿真与控制的基础.设JΨQ和JΨP分别为构型空间到驱动空间和工作空间的速度雅可比矩阵,则有
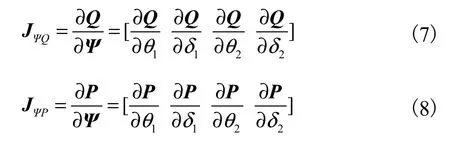
结合式(3)、(5)、(6),可以得到构型空间Ψ到工作空间 P之间的明确数学表达式,给定构型空间 Ψ与驱动空间 Q中的各个参数范围:θ1,θ2∈ [ 0 ,0.5π],δ1,δ2∈ [ 0 , 2π],L1=L2= 4 00mm ,可以得到两关节连续型机器人的整体工作空间分布,如图4所示.

图4 两关节连续型机器人工作空间示意Fig.4 Workspace of a two-joint continuum robot
2 连续型机器人灵活性分析
2.1 条件数指标k
目前,常用雅可比矩阵的条件数、奇异值、可操作度等来衡量机器人的运动灵活性.而在这些指标中,由Salisbury等[18]在1982年提出的条件数是最为通用的,即
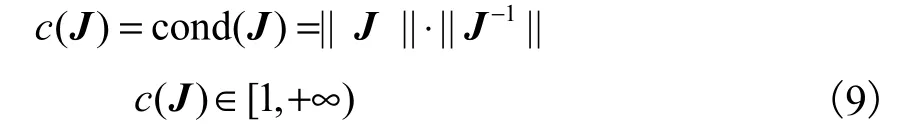
通常取条件数的倒数 k = 1 /c(J)作为衡量机器人灵活性的条件数指标,其反映了机器人末端点在工作空间内沿各个方向运动能力的均一性.当机器人以某一种构型到达工作空间中的任意一点时,该点的 k值越接近1,则该点的灵活性越好;反之,该点的k值越接近 0,则该点的灵活性越差;当k=0时说明该点为机器人构型中的奇异位置.
可以发现,当机器人的总长在一定范围内时,采用不同关节长度分配,对应的工作空间中灵活性分布也存在较大的差异,如图5所示.

图5 关节长度对工作空间中灵活性分布的影响Fig.5 Effect of joint length on the distribution of dexterity in the workspace
2.2 全域灵活性指标η
从上述分析中可以发现,机器人的条件数指标 k只能反映工作空间中某一点的灵活性,为一个局部指标.然而在操作机器人时,通常希望其在整个工作空间内的灵活性更好,因此,Gosselin等[19]基于条件数指标k,定义了全域灵活性指标η,即

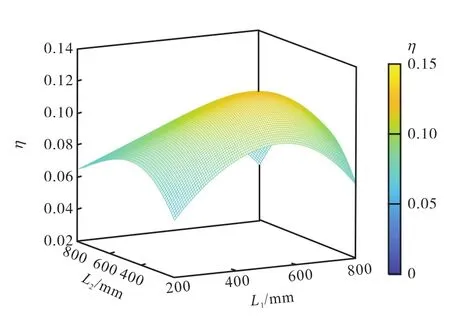
图6 关节长度分配对全域灵活性指标η的影响Fig.6 Effect of joint length on global dexterity index η
η越接近于 1,表明机器人在整个工作空间内的整体灵活性越好.
如图6所示,可以看出关节长度分配对连续型机器人整体灵活性的影响.
对于连续型机器人的结构设计来讲,一个重要的指标就是提升其在整个工作空间内的灵活性,因此,接下来将选用全域灵活性指标 η来指导连续型机器人的关节长度设计.
3 关节长度优化
3.1 目标函数建立
为了得到使得全域灵活性指标 η最大的连续型机器人最佳关节长度分配,建立目标函数
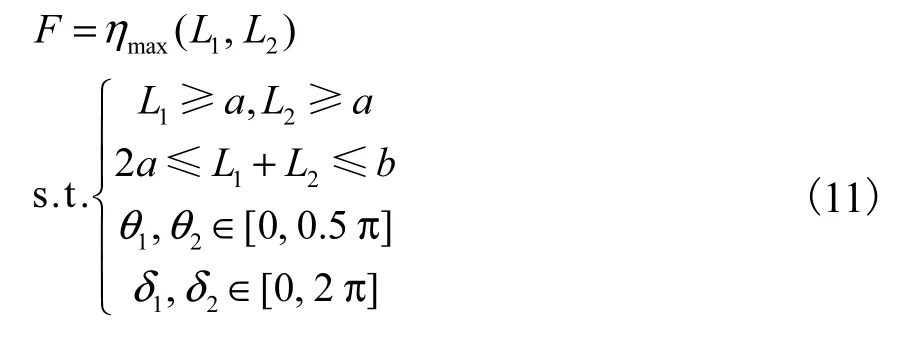
式中:a为每一关节长度的最小值;b为总关节长度的最大值.a,b的具体数值均可由实际情况来进行选取.在这里,为了保证机器人的关节长度比例协调,且总长不至于过长,取 a=200mm,b=1000mm,同时,为了便于机器人关节长度的设计,关节长度都取为10mm的倍数.
3.2 粒子群算法
粒子群算法[20]是近年来发展起来的一种仿生优化算法,其流程如图 7所示.与遗传算法相似,其也是从随机解出发,通过追随当前搜索到的最优值来寻找全局最优解,并利用适应度来评价解的品质.这种算法具有精度高、收敛快、操作简单等优点,广泛应用于学术与工程领域.

图7 粒子群算法流程Fig.7 Flowchart of the PSO algorithm
在本文中,引入粒子群算法来寻找使得全域灵活性指标η最大的最优关节长度L1与L2的值.机器人中其余结构参数的大小与范围与第 1节中描述相同.基于两关节连续型机器人的运动学模型(式(5)和(6))与雅可比矩阵的表达式(式(7)和(8)),在关节长度 L1与 L2构成的二维解空间中初始化一群随机粒子,在每一次迭代中,粒子通过在解空间中不断追随当前最优粒子的位置与速度,计算适应度,逐渐逼近最优解.重复进行多次迭代,最终确定使得全域灵活性指标η最大的关节长度L1与L2的值.
在 MATLAB中,根据式(11)中所示的目标函数、边界条件、优化变量以及上述算法流程编写 PSO程序,设定随机粒子种群大小M=40,迭代次数T= 2 0,学习因子 C1=C2= 1 .5,惯性权重ω=0.7.运行 PSO程序,针对 F这个目标函数,可以得到粒子群算法进化曲线以及优化后的关节长度与 F的关系曲线,如图8所示.
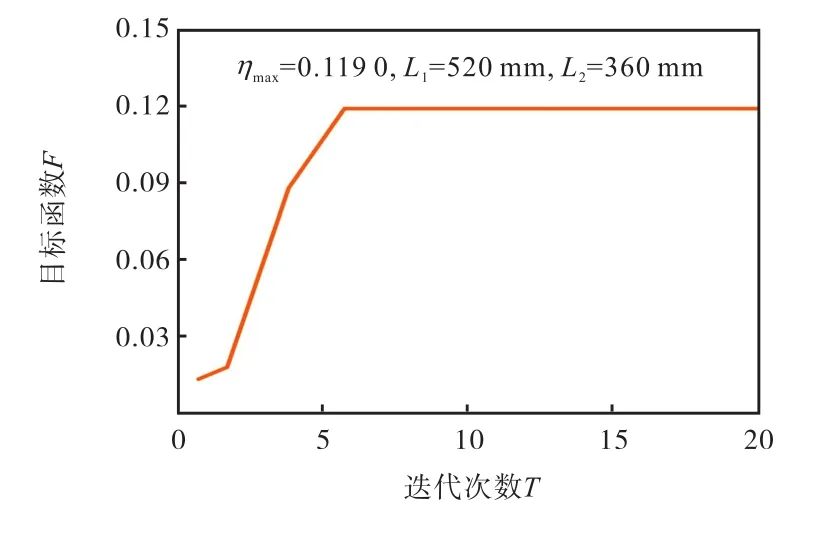
图8 全域灵活性指标η的PSO进化曲线Fig.8 PSO evolution curve of η
图8和表1表明了当机器人两关节长度为L1=520mm、L2=360mm时,机器人的全域灵活性指标η取得最大值 0.1190,也就是说机器人的整体灵活性最好.相比于传统的两关节长度相等的分配,优化后结果可以使机器人的整体灵活性提升10.29%.

表1 关节长度分配变化对η值的影响Tab.1 Effect of varying joint length on the value of η
4 仿真与实验
4.1 灵敏度指标
从第 3节的分析来看,可以通过调整机器人的关节长度分配来提升机器人在工作空间内的灵活性.接下来,将采用使得全域灵活性指标 η最大的关节长度分配 L1=520mm,L2=360mm 来设计连续型机器人,并对机器人的灵活性进行验证.由于基于雅可比矩阵条件数计算得到的机器人灵活性是一个抽象的概念,不能直观地进行实验验证,因此笔者提出利用可测量的灵敏度指标 S来间接反映机器人的灵活性,

式中 S表示机器人在某一状态下构型空间的单位扰动ΔΨ所引起的工作空间中末端位置变化ΔP的大小.显然,S值越大,表明机器人对输入量变化的响应越灵敏,机器人越灵活.
4.2 仿 真
为了方便进行仿真与实验验证,先绘制出关节长度分别为 L1=520mm、L2=360mm 的两关节连续型机器人的工作空间截面以及末端位置点所对应的条件数指标k的大小,并在工作空间截面内选择灵活性不同的两点 P1=[144.40,0,853.78]T与 P2=[439.41,0,639.42]T来分析机器人的灵敏度,从而验证可以用灵敏度来反映灵活性,如图 9所示.其中,P1和P2所对应的构型分别为Ψ1=[5°,0°, 30°, - 60°]T和Ψ2=[30°, 0°, 70°,- 60°]T;P1和P2所对应的条件数指标k分别为 k1= 0 .0565和k2= 0 .1507.

图9 工作空间中灵活性分布(L1=520mm,L2=360mm)Fig.9 Distribution of dexterity in the workspace(L1=520mm,L2=360mm)
为了比较机器人在 P1、P2灵活性不同的两点处的灵敏度分布情况,在 MATLAB 中,以Ψ1、Ψ2中当前的各个角度为圆心,在单位圆中随机找寻新的构型空间输入、,保证ΔΨ中各个角度的变化量满足式(13),从而可以得到新的末端位置、,便可以求得对应的ΔΨ与ΔP的大小.

重复进行上述步骤,而后利用式(12)便可得到机器人在 P1与 P2两点处的灵敏度分布情况.此外,为了便于看出灵活性大小与灵敏度分布的关系,在绘制灵敏度分布图时,将 P1和 P2都移至坐标原点,如图10所示.

图10 P1与P2两点灵敏度分布情况仿真示意Fig.10 Distribution of sensitivities at P1 and P2 in simulation

表2 灵敏度仿真结果Tab.2 Results for simulated sensitivity
综合对比图10与表2,可以发现灵活性好的点,其沿各个方向的灵敏度大小分布较为均匀,而灵活性差的点,其沿各个方向的灵敏度大小分布差异较大.
4.3 实 验
图 11为验证灵敏度与灵活性的实验装置,包括连续型机器人物理样机以及用于测量工作空间中末端位置的3D电磁追踪系统(误差小于0.5mm).

图11 实验平台Fig.11 Experimental platform
为尽量减小由于测量误差所带来的影响,在进行P1与 P2两点灵敏度实验时,各选取灵敏度分布截面中(图 10(c)、(d)所示)的最外侧轮廓 30个点所对应的构型空间作为实验中的输入,并用 3D电磁追踪系统来测量该输入下对应的机器人末端位置,从而得到末端位置变化ΔP的大小.
同时,为了验证按照 L1=520mm、L2=360mm的关节长度分配设计机器人时,其拥有更好的灵活性,改变采用模块化设计的机器人关节长度,在总长维持一定的情况下,让关节长度分配变为 L1=440mm,L2=440mm,将 P1与 P2两点对应的构型Ψ1与 Ψ2作为该长度分配下的输入,得到 P3与 P4两点,并按照上述仿真与实验步骤,对 P3与 P4两点进行灵敏度实验.
而后,利用式(12)便可得到实验状态下关节长度分配为 L1=520mm、L2=360mm 时机器人在 P1与P2两点处的灵敏度分布与大小的对比情况,以及关节长度分配为 L1=440mm、L2=440mm 时机器人在P3与 P4两点处的灵敏度分布与大小的对比情况,如图12、图13与表3所示.
综合对比图 10、图 12、图 13、表 2与表 3,可以发现实验与仿真结果差别不大,且对于相同构型输入,优化后得到的关节长度分配 L1=520mm、L2=360mm使得机器人的灵敏度沿各个反向分布更为均匀. 因此可以通过直观的灵敏度指标来验证机器人的灵活性,灵活性高的点,其各向灵敏度分布较为均匀.
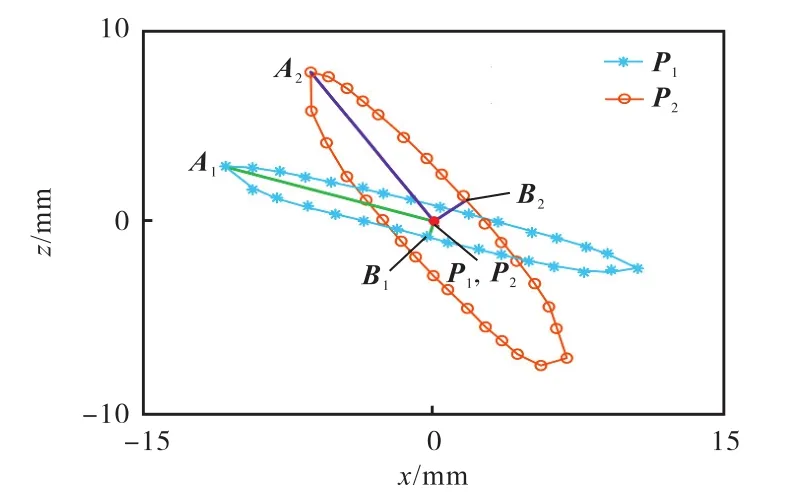
图12 P1与 P2两点灵敏度分布情况实验示意(L1=520mm,L2=360mm)Fig.12 Distribution of sensitivities at P1 and P2 in experiment(L1=520mm,L2=360mm)
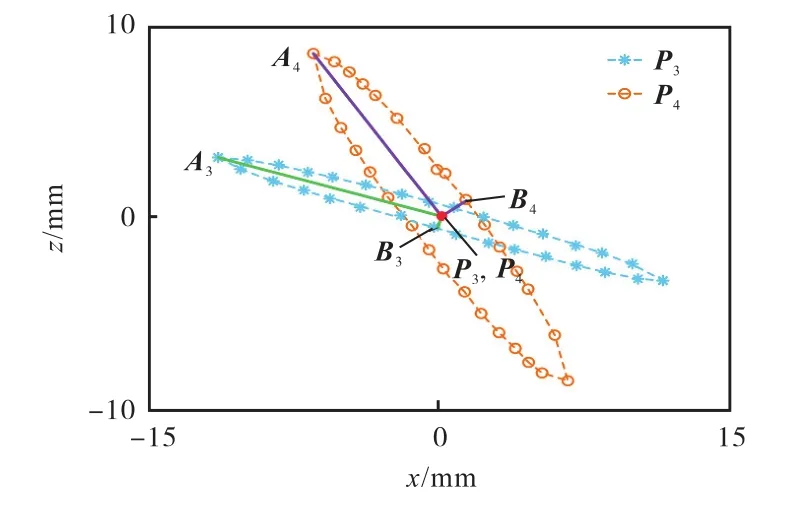
图13 P3与 P4两点灵敏度分布情况实验示意(L1=440mm,L2=440mm)Fig.13 Distribution of sensitivities at P3 and P4 in experiment(L1=440mm,L2=440mm)
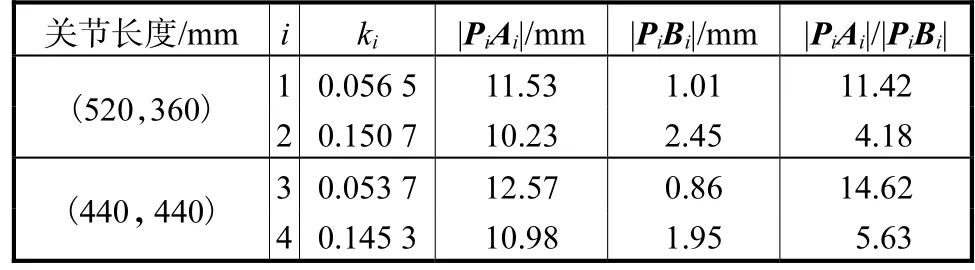
表3 灵敏度实验结果Tab.3 Experimental results for sensitivity
5 结 论
本文基于雅可比矩阵的条件数对连续型机器人的灵活性进行了详细讨论,而后在全域灵活性指标的引导下,通过粒子群算法得到了机器人的最优关节长度分配,并用于指导样机设计.在仿真与实验中,引入新指标灵敏度,直观地反映了灵活性的大小,发现根据雅可比条件数计算得到的灵活性较高的点其各向灵敏度分布亦较为均匀.本文的工作对于今后利用灵活性指导连续型机器人结构设计,以及直观验证机器人灵活性提供了一种新思路.

