一类长方形张量变分不等式解集的非空紧性

刘亚珍，凌 晨

(杭州电子科技大学理学院，浙江 杭州 310018)

0 引 言

变分不等式问题是非线性分析与最优化交叉领域的重要研究课题，在许多领域有广泛应用，如非均匀异性板平衡问题中的最优控制[1]、经济均衡模型转化成变分不等式问题[2]。当变分不等式的可行域为点闭凸锥时，变分不等式问题即为非线性规划中起重要作用的互补问题[3]。解的存在性是变分不等式问题重要的基本理论课题，针对变分不等式问题，利用各种例外簇概念，已有许多解的存在性结论。例如，Zhao Y.B.等在文献[4]中得到伪单调映射时的解存在性结果，Zhou S.Z.等[5]讨论了Hilbert空间中变分不等式问题解的存在性定理，Huang Z.H.[6]通过原问题的等价转换形式得到了一个新的存在定理。2017年，Wang Y.等[7]首次提出张量变分不等式问题，针对在非空闭凸集上为正定的正方形张量，给出了解的存在性定理。正如长方形矩阵一样，长方形张量是一类比正方形张量更一般的张量，其应用更为广泛。例如，在分类组合投资模型中提炼出的标准双二次优化模型，其最优性条件即为长方形张量变分不等式问题的一个特殊形式[8]。由于长方形张量变分不等式问题中出现两个独立的待求决策向量，其解的存在性研究难度更大[9]，文献[7]所得到的结论也无法直接用于长方形张量变分不等式问题。本文专注于讨论长方形张量变分不等式问题解的存在性，在其可行域上为半正定的条件下，得到了其解集为非空紧的。

1 问题描述

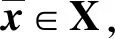
s.t.x∈X

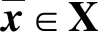
(1)

(2)

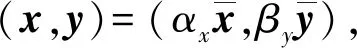
关于给定的点闭凸锥K⊆Rl和其对偶锥K*，有如下性质。

命题1.1[10]设K⊆Rl是一个点闭凸锥。若int(K*)≠∅，则对任何的u∈K{0}和v∈int(K*)，都有〈u,v〉>0，其中int(K*)表示K*的内点集。

2 解集的非空紧性

首先给出在研究一般VI(X,F)解的性质时起重要作用的定义和引理。

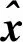
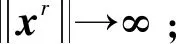
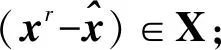
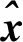
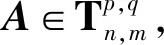
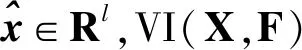
下面，给出本文的主要结果。

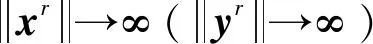
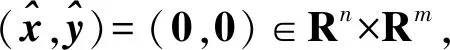
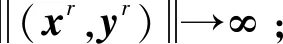
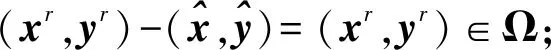
(3)

由式(3)及法锥的定义，可得

(4)

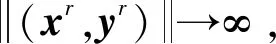
从而得到

(5)

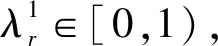
(6)

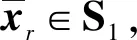
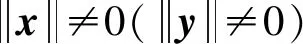
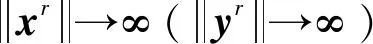
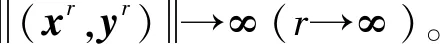
因为(xr,yr)∈SOL(A,a,b)，所以有

(7)

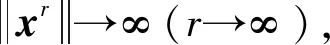
3 结束语

本文针对长方形张量变分不等式问题，利用例外簇的概念和性质，当长方形张量在可行域上为半正定时，得到解集是非空紧的，这是设计有效算法的理论基础。今后将针对长方形张量变分不等式问题解的有界性和误差界条件展开进一步研究。