R3上轮换点右保控线性映射

邓志颖，朱 军

(杭州电子科技大学数学研究所，浙江 杭州 310018)

0 引 言

近年来，对线性保控映射的研究取得了许多重要结论，并应用到量子信息等前沿领域。文献[1]梳理了有关受控关系和线性保控映射的研究成果及应用领域。文献[2-3]给出了Rn空间中线性保控映射的定义，并刻画了映射对应的矩阵形式。文献[4]将该映射对应的矩阵形式推广到矩阵空间Mn×m上，并给出以矩阵为研究对象的线性保控映射的形式。文献[5]提出行/列受控的概念，并刻画关于行受控和列受控的线性保映射和强线性保映射。文献[6]从局部入手，讨论了Rn空间中一点处线性保控映射的特征。本文针对R3空间中一组轮换点处右保控的线性映射进行研究，证明了该映射为线性保控映射。

1 若干定义与引理

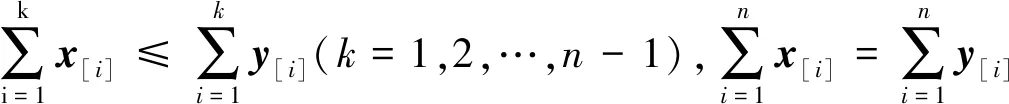
定义2[1]若存在一个n阶置换矩阵P使得x=Py，则称x与y是等价的，其中x,y∈Rn。

定义3[3]设Φ∶Rn→Rn是一线性映射。若对任意x,y∈Rn，xy，均有Φ(x)Φ(y)成立，则称Φ是一个线性保控映射。

定义4[6]设Φ∶Rn→Rn是一线性映射，非零向量y0∈Rn。若对任意x∈Rn，xy0，均有Φ(x)Φ(y0)成立，则称Φ在点y0处右保控。

引理1[1]若xy，yx，则x与y是等价的，其中x,y∈Rn。

引理2[2]设Φ∶Rn→Rn是一线性映射，则映射Φ是线性保控映射当且仅当以下其中之一成立：

(1)存在a∈Rn，使得对任意x∈Rn都有Φ(x)=tr(x)a；

(2)存在α(α≠0)，β∈R，P∈Pn，使得对任意x∈Rn都有Φ(x)=αPx+βtr(x)e，其中，Pn为全体n阶置换矩阵构成的集合，e=(1,1,…,1)T。

2 主要结论

定理设Φ∶R3→R3是一个线性映射，若Φ在各分量不相等的轮换点右保控，则Φ为线性保控映射。

证明设α1=(x1,x2,x3)T,α2=(x2,x3,x1)T,α3=(x3,x1,x2)T是R3中的一组轮换点，x1,x2,x3互不相等且x1+x2+x3≠0。因此，α1,α2,α3中必然存在一个升序或降序排列的点，不妨设α1降序排列，即x1>x2>x3。

设线性映射Φ在一组标准正交基下对应的矩阵为T，βi(i=1,…,6)为等价于像Tα1的点，其中β1=(y1,y2,y3)T,β2=(y2,y3,y1)T,β3=(y3,y1,y2)T,β4=(y1,y3,y2)T,β5=(y3,y2,y1)T，β6=(y2,y1,y3)T，不妨设y1≥y2≥y3。

设点α1,α2,α3在映射Φ作用下的像集为D，则D={Φ(α1),Φ(α2),Φ(α3)}。记集合D的基数为|D|，则|D|的取值为1，2或3。由Φ在各分量不相等的轮换点右保控及引理1可知，像Φ(αi)(i=1,2,3)相互等价。

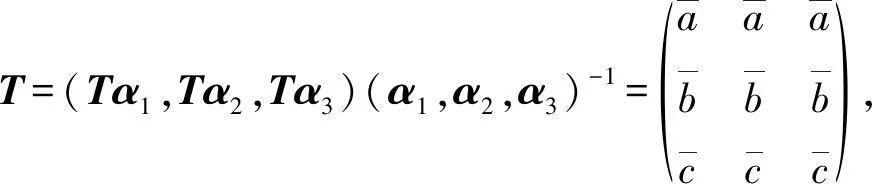
(2)若|D|=2，则Tαi(i=1,2,3)中有2个点重合，不妨假设Tα1=β1,Tα2=Tα3=β2。下面证明，存在不受Tα1控制的点Tα5，故不存在映射Φ使得各分量不相等的轮换点右保控。

设Tα5(3)为Tα5的第3个分量，考虑Tα5(3)与y1的差，计算可得：

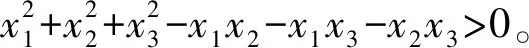
对于其它2个点重合的情形，可类似证明不存在满足定理要求的映射。

(3)若|D|=3，则Tαi(i=1,2,3)互不相等。接下来证明，Tα1,Tα2,Tα3互为轮换，映射Φ为线性保控映射。

对于y1=y2>y3的情形，βi(i=1,…,6)退化为3个互为轮换的点，即β1=β6,β2=β4，β3=β5，因此不妨设Tα1=β1,Tα2=β2,Tα3=β3。

设Tα5(3)为Tα5的第3个分量，考虑Tα5(3)与y1的差，计算可得：

因为Tα5(3)>y1，故Tα5不受Tα1控制，此时映射Φ不是轮换点右保控映射。

对于y1>y2=y3以及对应的轮换情形，可类似证明。

对于y1>y2>y3的情形，Tα1,Tα2,Tα3中至少有2个点互为轮换，不妨假设Tα1,Tα2互为轮换，考虑Tα1=β1,Tα2=β2。此时，Tα3有4种情形：

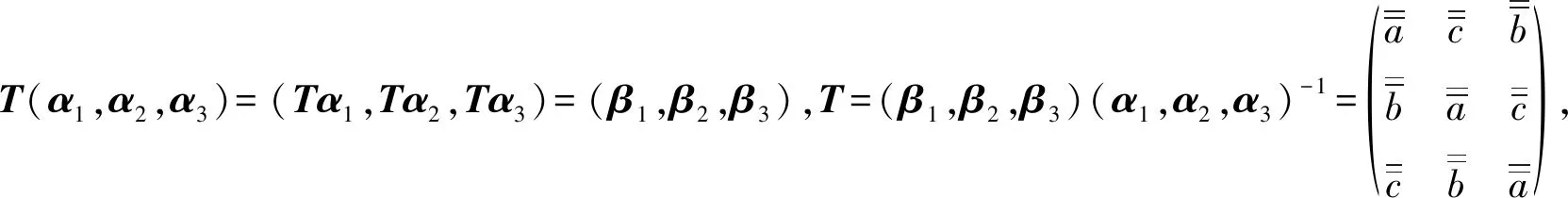
设Tα4=(z1,z2,z3)T，因为Tα4βi(i=1,2,3)，所以y1≥z1≥y3，y1≥z2≥y3，y1≥z3≥y3。因为故k≤0；又因此k≥0(其中，所以k=0。故z1=y1，z2=y3，z3=y1+y2+y3-(z1+z2)=y2，即Tα4=(y1,y3,y2)T=β4。同理可得Tα5=β5，Tα6=β6。

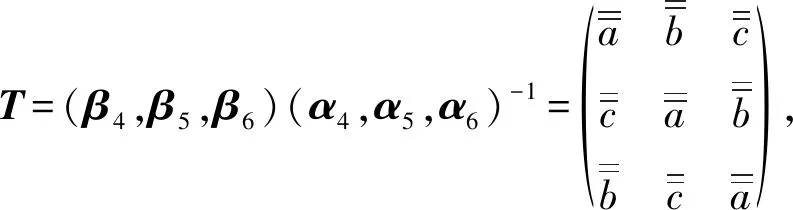
对于其它像为轮换点的情形，均可验证映射Φ为线性保控映射。

②若Tα3=β5，用反证法证明这样的映射不存在。假设映射Φ:(α1,α2,α3)→(β1,β2,β5)存在，其中β1=Tα1,β2=Tα2,β5=Tα3。下面证明，存在不受Tα1控制的点Tα5使其矛盾。

设Τα5(3)为Τα5的第3个分量，考虑Tα5(3)与y1的差，计算可得：

因为x1>x2>x3，y1>y2>y3，所以Tα5(3)-y1>0，即Tα5(3)>y1，故Tα5不受Tα1控制。

③若Tα3=β6，仿照第②种情形，假设映射Φ:(α1,α2,α3)→(β1,β2,β6)存在，其中β1=Tα1,β2=Tα2,β6=Tα3。下面证明，存在不受Tα1控制的点Tα6使其矛盾。

设Tα6(3)为Tα6的第3个分量，考虑Tα6(3)与y3的差，计算可得：

因为Tα6(3)-y3<0，即Tα6(3)

④若Tα3=β4，仿照第②种情形，假设映射Φ:(α1,α2,α3)→(β1,β2,β4)存在，其中β1=Tα1，β2=Tα2,β4=Tα3。下面证明，存在不受Tα1控制的点Tα6使其矛盾。

设Tα6(1)为Tα6的第一个分量，考虑Tα6(1)与y1的差，计算可得：

因为Tα6(1)-y1>0，即Tα6(1)>y1，故点Tα6不受点Tα1控制。

综上所述，若线性映射Φ在R3中各分量不相等的轮换点处右保控，则映射Φ为线性保控映射。证毕。

3 结束语

本文沿用文献[6]对一点处右保控线性映射的定义，对R3中各分量不相等的轮换点处右保控的线性映射进行研究，证明了该映射为线性保控映射。但是，本文仅讨论各分量不相等的点，没有考虑分量相等的点，今后将展开相关研究。此外，还可以考虑将定理推广到n维欧式空间，研究轮换点右保控线性映射与线性保控映射的关系。