一类具有时滞的非线性系统的指数稳定性

吕国栋，章春国

(杭州电子科技大学理学院，浙江 杭州 310018)

0 引 言

系统的动态行为不仅取决于系统的当前状态，而且还取决于系统的初始状态。实际系统中经常出现时滞问题，造成系统不稳定。近年来，时滞系统稳定性问题吸引了众多学者的注意。文献[1-2]主要考虑了时滞系统指数稳定性问题。文献[3]通过建立与相空间范数相关的能量泛函，讨论了时滞Karman Von方程吸引子的存在性。文献[4]研究了一类具有变系数时变时滞的记忆型Euler-Bernoulli板方程的局域非线性反馈衰减特性。文献[5]研究了一类具有时滞项的Timoshenko系统的反馈问题，并证明了该系统的稳定性。文献[6]研究了具有时滞的线性分布参数控制系统的渐近镇定问题，并给出了时滞偏微分方程组的应用。本文将文献中的相关结果推广到具有时滞阻尼的非线性系统中，给出一个在应用中易于验证的充分条件。

1 问题描述

本文研究时滞对具有阻尼非线性系统稳定性的影响。考虑以下初值问题:

(1)

为了得到系统的适定性，假设

(H1)A在H上生成指数稳定的C0-半群S(t)，即，存在常数μ>0和M≥0满足

(H2)f是满足局部Lipschitz条件的连续函数且f(0)=0，即，对于任意的φ1,φ2∈W存在正常数L>0满足

2 系统的适定性

下面给出系统 (1)适定性(即解是否存在、唯一且稳定)的证明。记算子T(t)

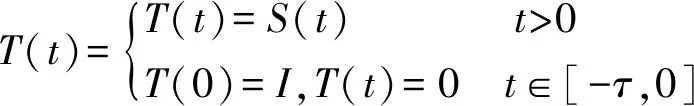
定理1如果假设(H1)和(H2)成立，那么抽象Cauchy问题 (1)存在唯一弱解：

(2)

证明首先证明y(t)是方程(1)的弱解。这里的迭代过程是标准的，详见文献[7]。选取y(0)(t)∈L2([-τ,+∞);)，满足

y(0)(t)=φ(t)t∈[-τ,0]，y(0)(t)=T(t)φ(0)，t≥0

令

(3)

第k次迭代表示为

(4)

当k=1时，由式(3)可知：t≥0时，有

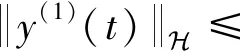
因此，对于任何正整数k，应用归纳法可得

(5)

因此，对于任意正整数k，应用归纳原理可得

(6)

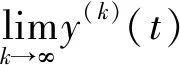
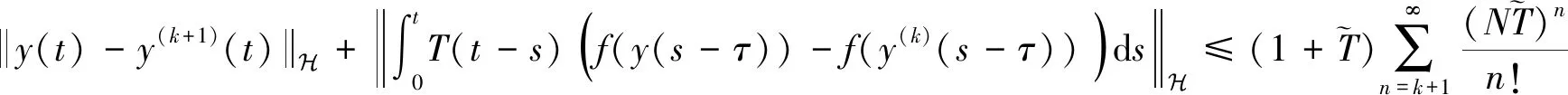
所以，y(t)满足积分方程(2)，即y(t)是方程(1)的弱解。

接下来，证明积分方程(2)解的唯一性。令z(t)是积分方程(2)的另一个连续解，则有

运用Gronwall不等式得到y(t)≡z(t)。证毕。

3 指数稳定性

下面证明系统式(1)在适当假设下的指数稳定性。

首先，考虑以下无时滞问题：

(7)

类似地，在条件(H1)和(H2)成立的情况下，式(7)存在唯一弱解：

(8)

和

(9)

运用Gronwall不等式，可得

(10)

接下来，对于t-τ>0和μ-ML>0，由式(4)和式(8)得

因此，得到

(11)

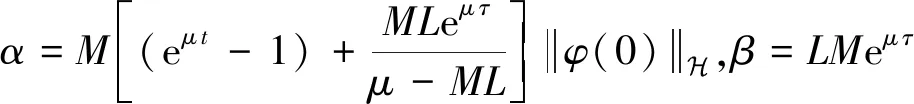
(12)

由Gronwall不等式得

(13)

假设系统满足条件(H3)：

μ-MLeμ τ≥0

综合上面的推理过程，有如下的结果：

定理2如果假设(H1)—(H3)成立，那么系统(1)是稳定的。

4 实例验证

通过文献[8]中的2个实例来验证所得结果的有效性。

例1考虑振动弦的边界镇定问题：

(14)

式中，c>0表示波速，α>0和α1表示边界阻尼系数，τ>0表示时滞。

设y=(w,wt)=(w,v),和D(y=(v,c2wxx)和

例2考虑一个具有分布阻尼的梁：

(15)

式中，a2>0表示弯曲刚度，γ>0和γ1表示分布阻尼系数，τ>0表示时间迟延。

设y=(w,wt)=(w,v),和D(y=(v,-a2wxxxx-2γv)及

综上，假设(H1)—(H3)成立，结合定理2，反馈控制系统(14)和(15)的解是指数稳定的。

5 结束语

本文研究了一类时滞对非线性阻尼系统的稳定性的影响。对于一个系统来说，时滞往往是系统稳定性变差或是变成不稳定的重要因素之一，因此，考虑具有时滞的系统十分有意义，当无时滞系统是稳定的，时滞在某个范围时，时滞系统仍能保持稳定性。今后将进一步考虑扩大时滞的范围以保证系统稳定性。