基于实测车流的悬索桥黏滞阻尼器多目标控制研究

赵 越，黄平明，龙关旭，刘焕举，孙亚民

(1.长安大学 公路学院，陕西 西安 710064；2.山东高速科技发展集团有限公司，山东 济南 250002)

0 引言

现代大跨径桥梁自重越来越轻，跨径越来越大，结构振动成为影响大跨径桥梁运营安全的关键因素。黏滞阻尼器自2000年在重庆鹅公岩长江大桥使用至今，作为一种常用的减震消能装置已广泛应用于桥梁抗震领域，其设置可以有效地减少结构在荷载作用下的振动响应，消耗外界输入的能量，保障结构安全运营。黏滞阻尼器设计时一般主要考虑地震荷载及风荷载作用下的减震控制效果[1-2]。近年来，通过多座大跨径桥梁的运营经验发现，黏滞阻尼器不仅可以在地震和风荷载作用下发挥效果，对车流等荷载作用下的结构响应也会产生影响。特别是对于大跨径悬索桥，在活荷载作用下加劲梁梁端产生显著的纵向位移是其结构本身的特征，而黏滞阻尼器可以有效减小悬索桥加劲梁梁端的位移响应，故考虑车辆荷载作用效应，充分发挥黏滞阻尼器的性能对于大跨径悬索桥的安全运营具有重要意义。

由于黏滞阻尼器的单向变形和受力特点，其在桥梁上的应用主要用于控制主梁纵向的响应，通常黏滞阻尼器都在主梁与桥墩(台)或相邻主梁之间纵向设置[3-4]。对于大跨径悬索桥，其横向的稳定性控制可以通过设置专用的抗风支座实现，无需将阻尼器成角度设置以保证其明确的受力和作用方向，所以关于阻尼器用于侧向控制的研究相对较少。已有的研究主要集中于黏滞阻尼器对桥梁结构在风荷载或地震荷载作用下响应的影响。黏滞阻尼器的作用方式决定了其振动控制效果主要通过试算方式进行，根据结构关键指标的响应情况验证黏滞阻尼器的设置是否满足要求。文献[4-5]分析了风荷载及地震荷载作用下黏滞阻尼器对大跨斜拉桥的振动控制效果，结果显示阻尼器对结构不同指标控制效果并不一致，阻尼器参数对其控制效果有重要影响，在地震和风荷载作用下存在最优阻尼器参数区间。文献[6]研究了大跨度公铁两用斜拉桥的黏滞阻尼器效应，指出阻尼器参数对列车制动力作用下主梁纵向位移会产生影响。文献[7-8]的研究指出,黏滞阻尼器可减少车辆作用下主梁的梁端位移，相应地减少伸缩缝变形的耗损，增加伸缩缝使用寿命。文献[9]的研究显示，考虑日常运营状态下梁端的纵向位移速度以确定设计最大阻尼力可改善阻尼器的耐久性。由于车流荷载对结构的作用方式与地震或风荷载有本质的区别，前者是长期的持续性作用，后者则具有突发性、高强度的作用特点，故二者作用下结构响应需关注的重点也不尽相同。同时车流作用下阻尼器参数对结构不同指标控制效果不一致，因此为更好地发挥黏滞阻尼器的性能，明确车流作用下结构响应的关键指标，选择黏滞阻尼器最优参数使得车流作用下的结构综合响应达到最佳十分必要。

本研究以一座典型大跨径悬索桥为工程背景，研究车流作用下黏滞阻尼器的振动控制效果，利用交通荷载监测系统采集的实际交通流数据，筛选出典型时段的车流，基于不同车流工况模拟形成高真实度车流，利用ANSYS的瞬态分析功能以集中力的方式模拟车辆各轴轴重进行加载，重点分析车流作用下黏滞阻尼器参数变化对桥梁结构响应的影响，进而对各阻尼器参数方案进行评价，采用变异系数法及TOPSIS法确定结构各指标权重，实现黏滞阻尼器的多目标优化控制。

1 车流作用下黏滞阻尼器作用分析

1.1 有限元模型

本研究以一座大跨径地锚式钢桁架悬索桥为背景，如图1所示。该桥主跨 896 m，主桥仅1跨钢桁架主梁，单向2.41%的大纵坡，跨中设置刚性中央扣。利用有限元软件ANSYS建立全桥模型进行分析。采用Beam4单元模拟主塔、主梁、盖板和墩柱；使用Link10单元模拟主缆和吊杆；通过Mass21单元模拟栏杆和桥面铺装；采用弹簧单元Combin14模拟伸缩缝。由于悬索桥主缆重力刚度对全桥影响较大，为保证结果的准确性，根据实测索力设置主缆和吊杆单元一定的初始应变。黏滞阻尼器一般布置方案为塔-梁处或辅助墩处顺桥向布置。根据该桥结构特点，在主跨两侧梁端塔-梁处顺桥向布置两个黏滞流体阻尼器，全桥共4个，如图2所示。

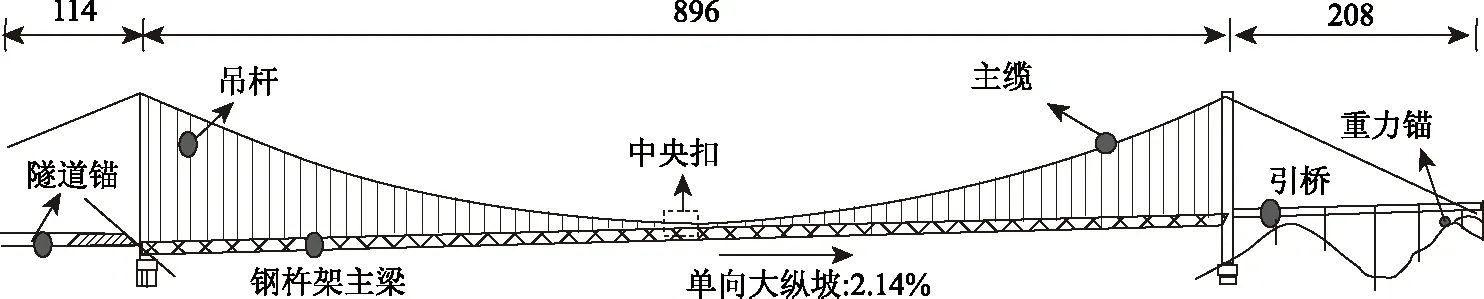
图1 悬索桥示意图(单位：m)Fig.1 Schematic diagram of suspension bridge (unit: m)

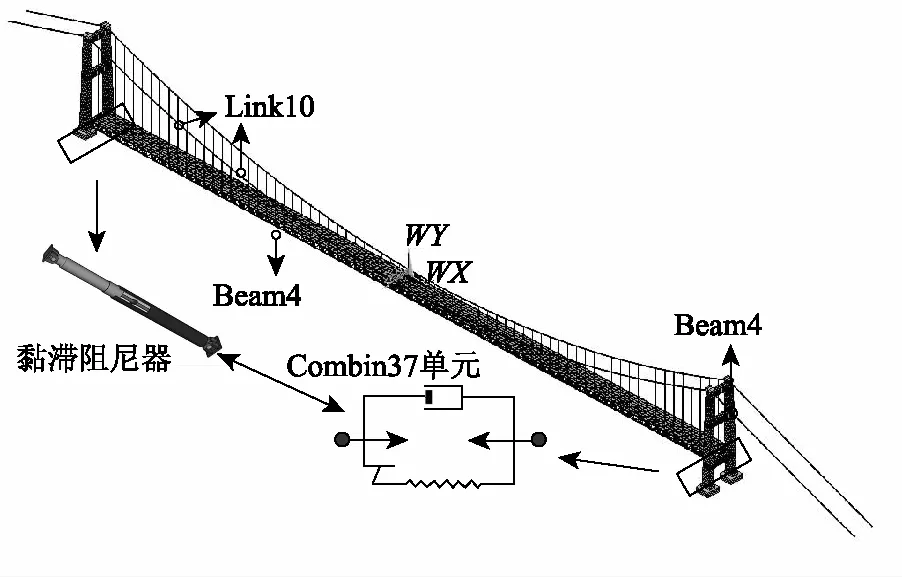
图2 有限元模型Fig.2 FE model

黏滞阻尼器的基本模拟方法及计算理论目前已较为成熟，由早期的线性模型发展至非线性模型，包括Maxwell模型、Kelvin模型、Wiechert模型和分数微分模型等，本研究采用规范[10]所推荐的阻尼力计算公式：

F=K|v|αsign(v)，

(1)

式中，F为阻尼力；K为阻尼系数；v为相对速度；α为速度指数，其范围为0.1～1。

采用Combin37单元可准确模拟黏滞阻尼器的特性[11]。定义合适的单元选项及实常数后，单元阻尼力如式(2)，其他实常数均取为0，定义好C1和C2即可准确模拟式(1)的黏滞阻尼器受力特性。

F=C1|v|1+C2sign(v)，

(2)

式中，C1为ANSYS中COMBIN37单元的9号实常数；C2为ANSYS中COMBIN37单元的10号实常数。

1.2 基于实测数据的交通流模拟

相比中小跨径桥梁，大跨径桥梁在车流作用下的响应主要受车流密度及车辆总重的影响[12]。为了更真实地分析车辆作用下黏滞阻尼器的效应，本研究基于交通荷载监测系统获得的某地区实测交通流，选取其中代表性时段的数据模拟形成车流进行加载，具体流程见图3。

图3 交通流模拟流程Fig.3 Flowchart of traffic flow simulation

图4为将所采集的数据进行分时段分车道统计得到的每小时车辆总重极值。

图4 小时车辆总重极值Fig.4 Extreme values of hourly gross vehicle weight

选取极值时段的车流数据，计算得到如图5所示的不同时刻车长分布频率图，并计算该时段超车道和行车道的平均车长数据。为保证车辆安全行驶，拥堵车速为vd为9 km/h[13]。

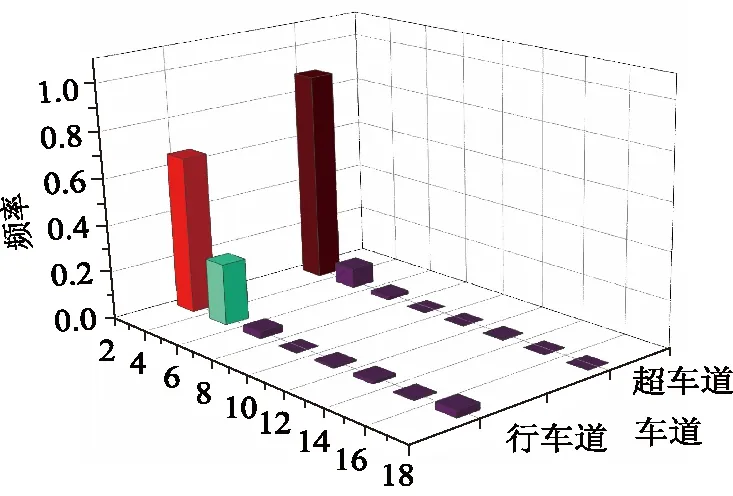
图5 车长分布Fig.5 Distribution of vehicle length

根据式(3)得到车辆阻塞密度Kd:

(3)

式中，d1为实测平均车长；d2为车辆间最短安全距离，通常由平均车速v和驾驶人制动反应时间t确定，在本研究中，设驾驶员反应时间满足正态分布[14-15]，选取t为2.2 s。

实际桥梁上下游交通状况并不一致，本研究定义每侧的行车道与超车道车流状况一致，上下游两侧不一致。将车流工况划分为密集车流0.7Kd和稀疏车流0.2Kd，一侧采用密集车流，另一侧采用稀疏车流双向对开。结合格林希尔兹经典模型(式4)计算车流密度对应的平均车速。最终形成基于实测交通流的车流关键参数，见表1。

(4)

式中，Kd为车辆阻塞密度；K为车流密度；vf为自由流车速，在这里取设计速度100 km/h。

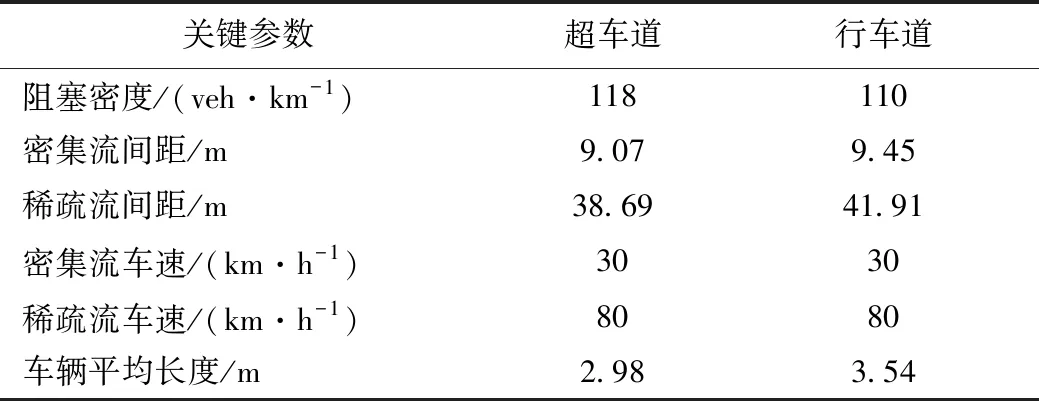
表1 交通流关键参数Tab.1 Key parameters of traffic flow

采用MATLAB生成车流数据，利用ANSYS中的瞬态分析功能，以集中力的方式模拟车辆各轴轴重进行加载。

1.3 车轮荷载加载

在实际荷载加载过程中，车辆作用位置不一定在桥梁有限元模型的节点处，当工况较多时，荷载信息输入繁多，容易出错，因此本研究基于ANSYS参数化设计语言编制车辆自动识别加载的宏命令。

车流作用下公路车桥耦合时的交通流量大，车流随机分布性强，分析车桥耦合的关键问题在于车桥接触点的定位和加载。对于常用的模拟桥梁结构的有限元模型，例如梁格模型、实体模型或板壳单元模型，在车辆做静力加载时，车辆荷载通常简化为集中力向临近4个节点分配，见图6。在二维平面内四边形荷载分担方式与位移插值函数一致。当车轮荷载P作用于坐标(x,y)处时，引入4节点等参元映射关系，见图7。

图6 车轮荷载分配示意图Fig.6 Schematic diagram of wheel load distribution注: F为车辆荷载简化的集中力；F1,F2,F3,F4分别为分配至4个节点的作用力。

图7 四节点等参元关系Fig.7 Four-node isoparametric element relation

坐标映射关系如式(5)所示：

(5)

式中，x，y为车轮荷载着力点坐标；Ni(i=1,2,3,4)为车轮荷载P临近4点的分配系数；xi，yi为临近4点的物理坐标；ξ，η为x，y从四边形单元映射到母单元对应的值；ξi，ηi分别为母单元的第i个节点的横、纵位置。

双线性方程组式(5)可通过牛顿迭代法[16]求解，进而计算出分配系数Ni，从而实现车轮荷载的自动加载。

2 车流工况下黏滞阻尼器参数分析

黏滞流体阻尼器设计规范[8]中将阻尼器按速度指数分为7级，分别为0.1，0.2，0.3，0.4，0.5，0.6和1，对阻尼系数则无明确规定。本研究选择7级速度指数下，阻尼系数C分别为1 000，2 500，5 000，7 000，10 000，15 000,20 000 kN/(m/s)α, 计算结构的响应。

2.1 黏滞阻尼器阻尼力分析

阻尼力是黏滞阻尼器性能的关键指标，规范中对黏滞阻尼器按照阻尼力分为17种规格， 最大为4 000 kN。本研究计算车流作用下各参数黏滞阻尼器的最大阻尼力。

图8为车流作用下不同速度指数阻尼器的阻尼力时程曲线。可见各参数阻尼力相差较为明显，但总体变化趋势基本一致。

图8 不同速度指数阻尼力时程曲线[C=5 000 kN/(m/s)α]Fig.8 Time history curves of damper force in different velocity exponents [C=5 000 kN/(m/s)α]

图9给出了各参数最大阻尼力变化情况。阻尼力随速度指数的减小而增大，且与阻尼系数呈线性变化，速度指数越小，随阻尼系数增大的速度越快。部分参数阻尼器的最大阻尼力已经超出了规范分类的常规阻尼器，本研究出于研究目的依然予以分析。

图9 车流下各参数最大阻尼力Fig.9 Maximum damper force of different parameters under traffic flow

图10为不同速度指数阻尼力与速度的关系。速度小于1 m/s时，速度指数越小，阻尼力越大。速度大于1 m/s时，速度指数越大，阻尼力越大。阻尼力与速度的关系接近于线性变化。

图10 阻尼力与速度指数关系[C=5 000 kN/(m/s)α]Fig.10 Relationship between damper force and velocity exponent [C=5 000 kN/(m/s)α]

表2给出了部分参数阻尼器在车流作用下的阻尼器速度。可见车流作用下阻尼器的运动速度远小于1 m/s，此范围内速度指数越小，阻尼力越大，阻尼力与速度的关系呈抛物线变化。

表2 车流下阻尼器最大速度(单位：m/s)Tab.2 Maximum damper velocity under traffic flow(unit: m/s)

2.2 黏滞阻尼器控制效果分析

截取车流工况下结构的关键参数指标，选取主梁、主塔、主缆及吊杆典型指标进行分析，包括主梁梁端纵向最大位移、主梁梁端累计位移、主梁跨中弯矩、主塔塔顶位移、主塔塔顶加速度、主塔塔根弯矩、主缆力以及吊杆力。

2.2.1对主梁的影响

主梁关注的指标以梁端纵向最大位移、梁端纵向累计位移、主梁跨中弯矩为主。梁端纵向累计位移统计了车流作用时间内，主梁端部相对于基准状态纵向往返运动的位移绝对值之和，同时以这一时间内位移的最大绝对值作为梁端纵向最大位移。伸缩缝及支座等附属构件寿命通常与构件在荷载作用下的变形及疲劳性能有关。研究显示，伸缩缝、阻尼器或支座的摩擦滑动累计距离超出设计值是导致构件破坏的重要因素，而其中车流作用是梁端累计运动位移的主要来源[7]。因此，梁端纵向累计位移的减少意味着与之相关构件寿命的延长，并且梁端最大位移也决定了相关构件是否处于正常工作范围内，是体现阻尼器对主梁纵向振动控制效果的重要指标[8]。

图11为梁端纵向累计位移时程。可见黏滞阻尼器不同速度指数或阻尼系数对应的梁端纵向累计位移时程变化趋势基本一致。

图11 梁端纵向累计位移时程Fig.11 Time history curve of accumulated longitudinal girder displacement

图12、图13分别为梁端纵向累计位移和梁端纵向最大位移响应。两种响应均随阻尼系数增大或速度指数减小而减小，减弱率随阻尼系数增大逐渐减小至趋于平缓。无阻尼器时车流作用下梁端累计位移为4.594 m，阻尼器作用下梁端累计位移最多减少56.36%～2.005 m。梁端纵向最大位移的变化趋势与累计位移基本一致，梁端最大位移最多可由无阻尼器的0.611 m减小31.55%～0.418 m。

图12 梁端纵向最大累计位移Fig.12 Maximum accumulated longitudinal girder displacement

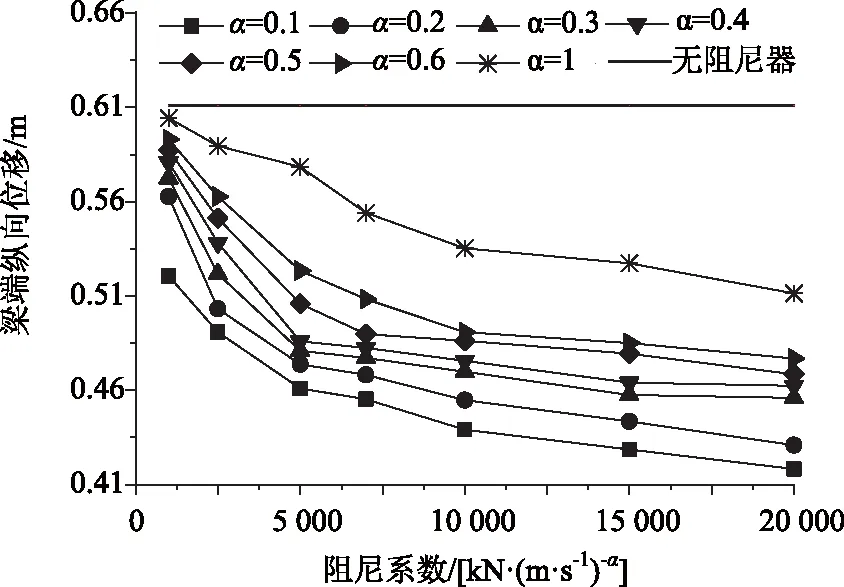
图13 梁端纵向最大位移Fig.13 Maximum longitudinal displacement of beam end

图14为主梁跨中弯矩的变化情况。跨中弯矩随速度减小或阻尼系数增加而减小，速度指数小于0.3时，弯矩随阻尼系数减弱速度较快，超过0.3则趋于平缓。在阻尼器作用下主梁跨中弯矩最多可减小6.08%。

图14 主梁跨中最大弯矩Fig.14 Maximum bending moment of girder mid-span

2.2.2对桥塔的影响

分别提取不同阻尼器参数时车流对桥塔结构的作用效应，包括塔顶位移、塔根弯矩和塔顶纵向加速度。如图15、图16所示，塔顶位移和塔顶纵向加速度变化趋势总体一致，都随着阻尼系数的增大或速度指数减小而减小。

图15 塔顶纵向最大位移Fig.15 Maximum longitudinal displacement of pylon top

图16 塔顶纵向加速度Fig.16 Maximum longitudinal acceleration of pylon top

塔底弯矩变化见图17，当速度指数α<0.3时，塔底弯矩随阻尼系数增大而增大，当速度指数0.3≤α<1时，随阻尼系数先减小后增大，当速度指数α=1时，随阻尼系数增大而减小。减弱率方面，塔顶位移及塔底弯矩均较小，都在1%以内。塔顶纵向加速度的减弱效果较为明显，最大可达30.35%。

图17 塔根最大弯矩Fig.17 Maximum bending moment of pylon root

2.2.3对主缆的影响

图18、图19分别给出了主缆力及吊杆力的响应。随着阻尼系数增大，主缆力呈增大趋势，而吊杆力呈减小趋势。当阻尼系数不变时，主缆力极大值随速度指数的增加而减小，吊杆力随速度指数的增大而增大。主缆力及吊杆力受阻尼器参数变化影响较小，主缆力最大变化率仅为0.45%，吊杆力的最大变化率仅有0.88%。

图18 主缆力最大值Fig.18 Maximum main cable force

图19 吊杆力最大值Fig.19 Maximum suspender force

3 最优阻尼器参数确定

黏滞阻尼器参数影响面广，涉及指标较多，一般常采用试算并进行非线性规划的方法确定最优阻尼器参数[17]。拟合函数存在误差，各指标的权重也无明确标准，且不便于灵活调整。本研究采用变异系数法客观确定各评价指标的权重，消除各项评价指标量纲不同带来的影响，然后利用TOPSIS方法确定最优响应指标，根据各方案响应指标到最优响应指标的距离来寻找最优参数方案。

变异系数法作为一种客观赋权方法，直接利用各项指标所包含的信息，通过计算得到指标的权重。指标取值差异越大的指标，也就是越难以实现的指标，其变异系数也越大[18]。TOPSIS法通过检测评价对象与最优解及最劣解的距离来进行排序，可以客观地对多指标情况下各方案进行综合评价，概念清晰，可操作性强[19]。具体步骤见图20。

图20 最优参数确定Fig.20 Determination of optimal parameters

变异系数法直接利用各项指标所包含的信息，对于有n个指标的赋权对象，通过式(6)计算得到指标的权重：

(6)

确定各指标权重后，即可利用TOPSIS方法进行参数评价。设决策问题有n个可行解，m个评价指标。首先根据各参数方案对应的结构评价指标的值构成决策矩阵A。

(7)

依据式(8)将决策矩阵参数规范化，根据各指标的权重构建规范化加权决策矩阵Z。

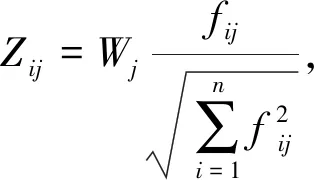
(8)

式中，fij为决策矩阵A的参数，i=1,…,n,j=1,…,m；Wj为第j项指标的权重。

(9)

表3为得到的各指标变异系数以及权重。可见，主梁的纵向最大位移、累计位移及塔顶纵向加速度变异系数及权重较大，说明阻尼器参数对3者在车流作用下的变化影响比较明显。吊杆力、塔底弯矩及塔顶纵向位移变异系数及权重较小。得到各指标权重后，按式(7)和式(8)计算得到规范化加权矩阵，并确定理想解Z+和负理想解Z-。

表3 变异系数及权重Tab.3 Variation coefficient and weight

进一步，按式(9)计算得到各参数方案的相对接近度结果。

表4选取了所有车流下黏滞阻尼器阻尼力小于4 000 kN 中接近度排名前10位的方案。根据分析结果，速度指数对车流下结构响应的影响更明显，速度指数小的阻尼器可在慢速运动时发挥更好的控制作用，对结构在车流作用下响应的控制效果更好。依据规范计算各参数组合下阻尼力4 000 kN时对应的设计最大运动速度[10]。结果显示，尽管阻尼系数增大有利于减小结构在车流作用下的响应，但阻尼系数增大时对应的最大设计速度减小，不利于阻尼器在极端状况下的工作性能。阻尼系数5 000 kN/(m/s)α，速度指数0.1时结构响应各指标最接近理想解，但此时车流作用下阻尼器最大阻尼力已达3 593 kN，接近其极限工作状态，当阻尼系数2 500 kN/(m/s)α，速度指数0.1时，阻尼器最大阻尼力仅有1 805 kN，仍有较大工作空间，相对应的最大设计速度可达109.95 m/s，能广泛适应各种情况。

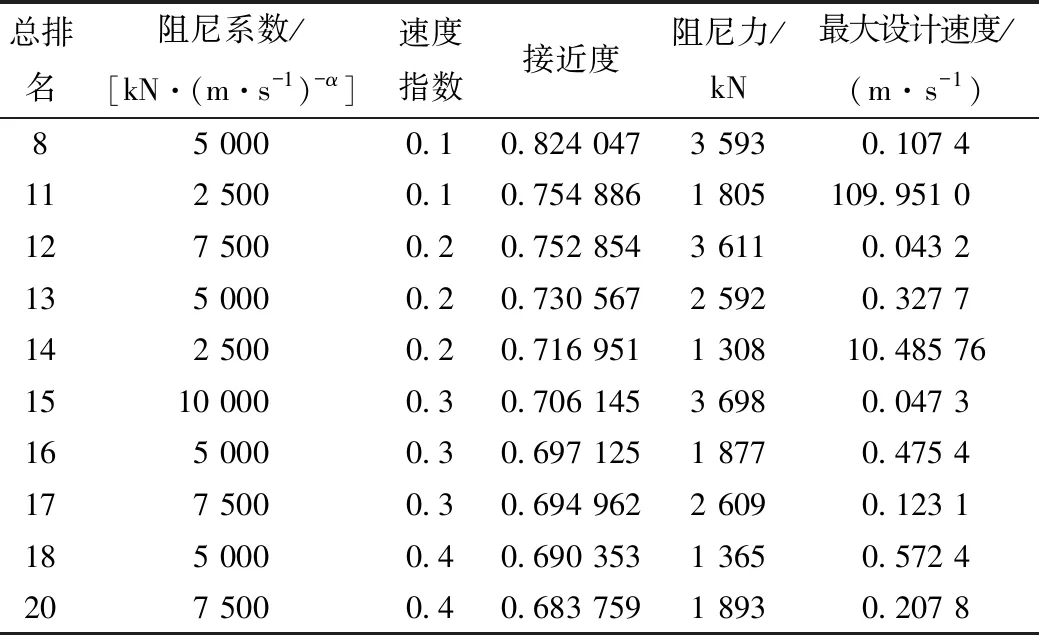
表4 各参数相对接近度Tab.4 Relative proximity of each parameter

4 结论

针对黏滞阻尼器在大跨度悬索桥中的应用，本研究利用交通流实测数据模拟形成真实运营荷载下的高真实度车流，基于等参元方法将车辆荷载简化为集中力荷载进行加载，研究了不同参数阻尼器对车流作用下桥梁结构响应的影响，并利用变异系数法及TOPSIS法对各参数方案进行了评价，结论如下：

(1)车流作用下，黏滞阻尼器对桥梁结构的影响不可忽略，应当作为黏滞阻尼器设计的考虑因素。黏滞阻尼器可有效降低车流作用下的梁端累计位移、梁端最大位移及塔顶纵向加速度响应，阻尼器对塔顶位移、塔根弯矩、主缆轴力及吊杆力的影响并不明显。

(2)车流作用下，梁端纵向最大位移、累计位移，主梁跨中弯矩、塔顶纵向位移、塔顶纵向加速度及吊杆力均随着阻尼系数增大或速度指数减小而减小。当速度指数<0.3时，塔底弯矩随阻尼系数增大而增大，当速度指数0.3≤α<1时，塔底弯矩随阻尼系数增大先减小后增大，当速度指数α=1时塔底弯矩随阻尼系数增大而减小。主缆轴力随阻尼系数增大或速度指数的减小而增大。

(3)根据分析结果，在车流作用下最优的阻尼器参数应当为C=2 500 kN/(m/s)α，α=0.1。阻尼器速度指数变化对车流作用下结构响应的影响更为明显，速度指数越小，阻尼器的控制效果越好，可明显提高车流作用下的振动控制效果。阻尼系数增大亦可提升控制效果，但阻尼系数过大会导致阻尼器长期处于高负荷工作状态，不利于构件的耐久性。较小的阻尼系数对应的最大设计速度更大，能更好地应对极端工作状况。

(4)利用变异系数法及TOPSIS法分析评价不同阻尼器参数对结构响应的影响，可以科学地确定各指标的权重，并且全面地对结构响应指标进行综合考虑，具有适用性强、计算简便、精确度高的特点，可以进一步应用于综合考虑地震，风荷载及车流荷载综合作用下的阻尼器参数确定。