考虑用户紧急程度的在途路径诱导策略研究
白 静,陈业华,刘一健
(燕山大学 经济管理学院,河北 秦皇岛 066004)
0 引言
随着交通基础设施的不断完善以及数据传输、数据处理等技术的快速发展,车载路径诱导系统的研究和应用获得了新的契机,用户可以通过导航系统提供的实时信息选择较优线路。目前很多学者对基于实时信息的路径寻优作了深入研究,其中所采用的最直观的决策方法是寻找最短路径,为了解决行驶时间概率分布不确定的问题,Cao等利用每条路径上的采样行驶时间将原始的求最短路径问题转换成基数最小化问题进行求解[1]。考虑到时间问题造成行驶成本具有很大的不确定性,智路平等对动态的交通行驶成本进行分类预测,并在相应的可靠性约束下利用改进的Dijkstra法作出寻优决策[2],此外,林徐勋[3]、杨传印[4]等也分别利用概率密度演化理论、优先队列方法求解了行驶成本不确定的最短路径问题[3-4]。还有学者进一步研究了当用户对路径选择没有确定性标准时的选择模型,其中,张惠玲等人考虑了用户的出行需求对规划方案的影响,利用级差效益衡量用户这一主观感知,并作为路径选择的评价准则[5]。Mai[6]、Songyot[7]、Kitthamkesorn[8]等学者则分别从随机用户均衡的角度建立了路径选择模型。对交通数据的不同处理方式将诱导类型划分成反应型及预测型二类。反应型策略根据实时的路况信息制定路径诱导策略,Nejad[9]等设计了层级算法以处理ITS获取的实时数据,进而计算最短路径。此外,TomTom[10]、google[11]等企业也已着手开发车、路通讯下的路径诱导系统。但反应型策略的特点是根据当前路况作出相应决策,而交通状态是不断变化的,当前的最优决策可能会将车辆转移至相对延迟拥堵的路线,诱导效果存在随机性。预测型策略是利用预测的信息制定诱导方案,即在决策前首先利用交通数据对未来交通状态作预测。Lin[12]等提出了动态在途实时路径决策方案(DEDR),该方案引入了信任概率评价预测信息,并构建相应的多重矩阵为用户提供路径选择依据。预测型诱导策略兼顾了坏天气或突发事件造成的交通状态不确定性,实用性更强[13-15]。
考虑目前多数文献缺乏对突发事件造成突发拥堵的嵌入研究,而用户面对这类包含不确定性、衍生性等特点的交通状况所作出的反应与常态化拥堵有所区别。而且,多数诱导系统采取依据实时数据的反应性决策,在交通状况波动较大的突发拥堵情境下具有一定滞后性,针对上述问题,本研究考虑在诱导系统中设置针对突发拥堵的导航模块,当系统识别突发拥堵发生时,自动触发突发拥堵导航模块,针对拥堵状况为用户提供实时的在途路径诱导策略。为提高用户体验进而提高用户对诱导系统的服从率,在深入分析用户对拥堵的个人感知特性基础上,以感知拥堵作为路径诱导的路径分配限制因素,设计了基于用户紧急程度的随机均衡替代路线分配方案。同时,为了充分利用预测信息提高路径寻优效率,将预测的交通信息作为诱导决策的信息支持,并提出了时变路网下改进的A*算法。
1 突发拥堵下考虑用户紧急程度的在途路径诱导策略
路径诱导作为常规性的交通管理措施,能够应用于日常交通中,特别是对于突发拥堵状况,用户能够凭借诱导系统显示的道路信息决定行驶路线。本研究设计了一个针对突发拥堵的动态在途路径诱导方案(EPR)。突发拥堵时,诱导系统周期性执行4个程序对路线进行再分配:
(1)数据搜集及处理;
(2)交通拥堵预测;
(3)选取改变路线车辆;
(4)为被选车辆计算备选路线信息。
这里(1)、(2)采用文献[16]提出的深度结构预测模型。EPR重点讨论(3)、(4)部分。
当突发事件发生并触发突发拥堵导航系统时,该模块将启动对即将进入拥堵区域车辆的确认程序,显然,拥堵状态下车辆的驶入将加剧交通堵塞,为避免交通进一步恶化,本研究选择“L等级”标准,视拥堵程度科学地选择合理位置车辆并诱导其更改行驶路线。具体来说,L作为设定的诱导区域范围值,即选择在交通流逆方向上距离事发路段为L内的部分车辆进行路径诱导,假定L=2,车辆选择的方法如图1所示。其中,系统识别Sc路段为突发拥堵状态,以Sc为中心沿车流流入方向划出2级路段,分别为S1,S2,并依次圈定S1及S2中需更改路线车辆。车辆选择的方法如图1所示。
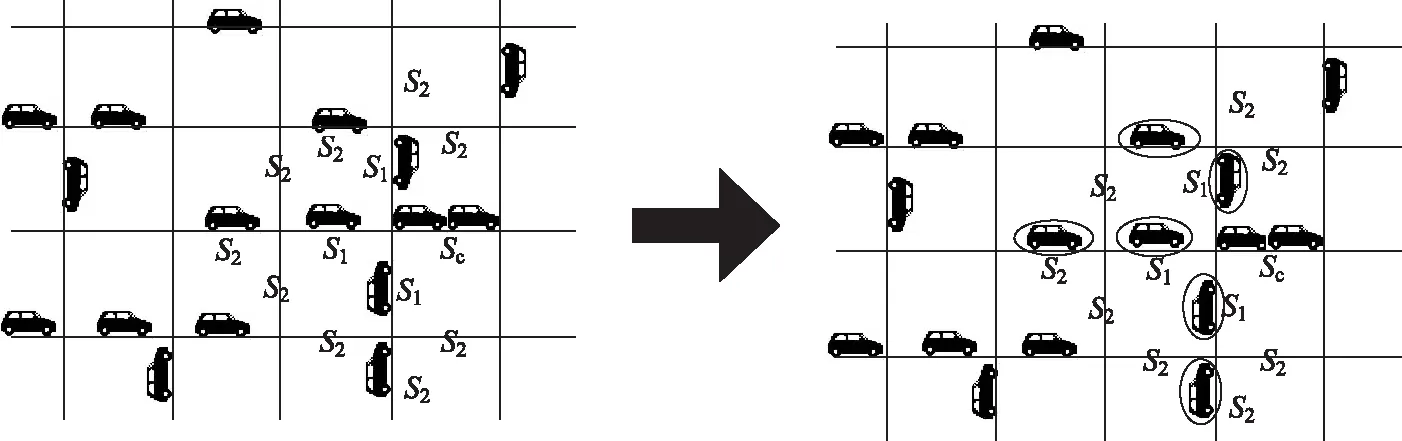
图1 车辆选择过程Fig.1 Vehicle selection process
选出需更改路线的车辆后,利用改进A*算法计算前k条次优路径,同时为其分配备选路线。
1.1 时变路网下的改进A*算法
考虑到突发拥堵下的路径诱导对时效性要求更高,本研究采用具有高效、直接特性的搜索算法A*算法求解最短路径。在交通网络中,行驶成本具有很大的不确定性,对于不同时间点,行驶成本会存在较大差异,特别是发生突发性拥堵时,会进一步增加行驶成本。因此,本研究采用具有时间依赖的A*算法结构,并通过改进A*算法中行驶时间的表达,采用交通流预测信息与历史信息表示未来的行驶时间。
A*算法作为典型的启发式算法,通过路径代价点的评估函数指引寻优行为的前进方向。假设从s点出发,终点为d,A*算法的目标就是找到s→d的最佳路径。搜索过程分为两个阶段:(1)判断迈出一步(出发点s到节点vi)的行驶成本,记为g(vi),本研究用行驶时间表示。(2)节点vi到终点d所需直接步数(本研究指最优路径行驶时间评估函数),记为h(vi)。令评估函数f(vi)表示为:
f(vi)=g(vi)+h(vi)。
(1)
通过计算并存储f(vi),找到各方向中使f(vi)最小的路径即可。其中,在具有时间依赖的A*算法中,假定出发时间点t,去往节点k的评估函数为h=h(k,t)≥0。
设计科学的评估函数有助于有效、快速地寻找到最短路径。时变网络中路段的行驶成本并非固定值,常见方法是利用实时路况信息或者历史数据求取行驶成本,而突发事件会造成交通状态急速改变,利用现有状态信息计算得到的路径寻优结果甚至可能不再符合未来短期内交通状态,因此本研究在时间依赖的A*算法基础上利用预测信息改进评估函数h(vi)的表达,更精确地求解最短路径。
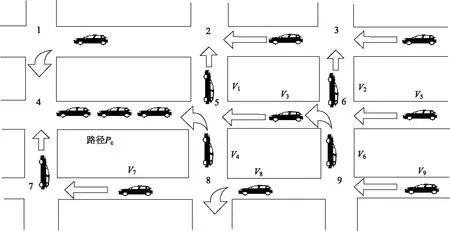
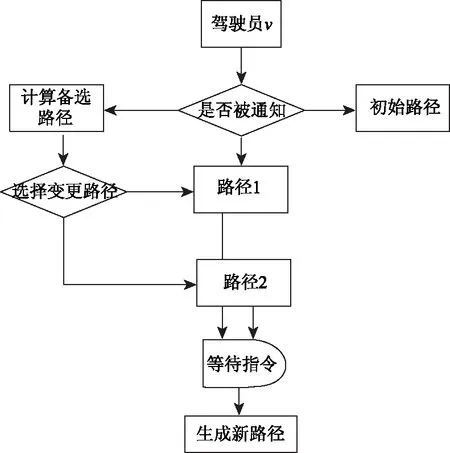
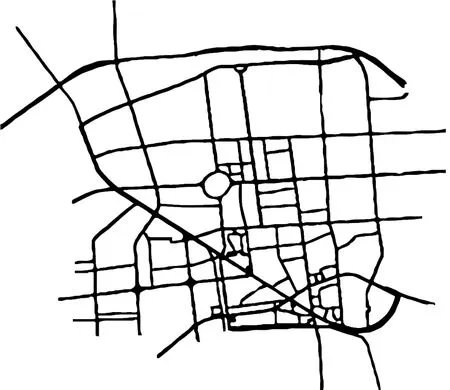
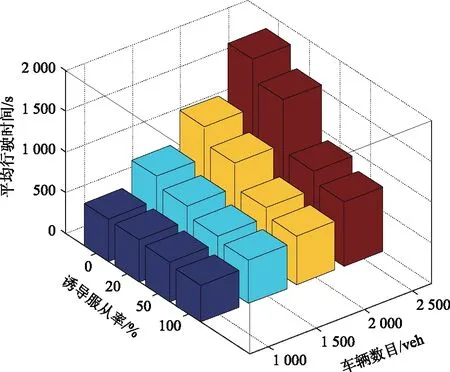
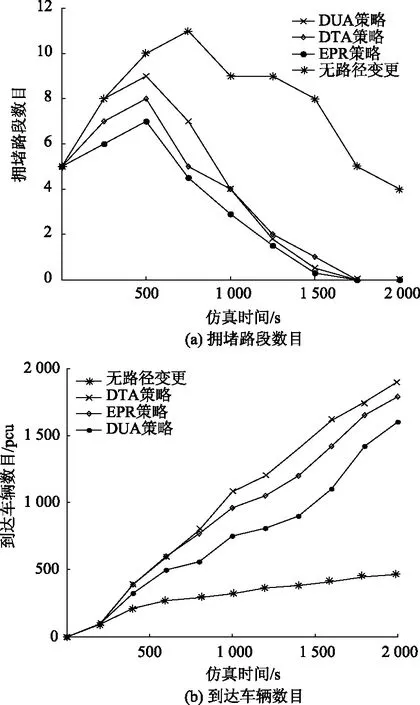
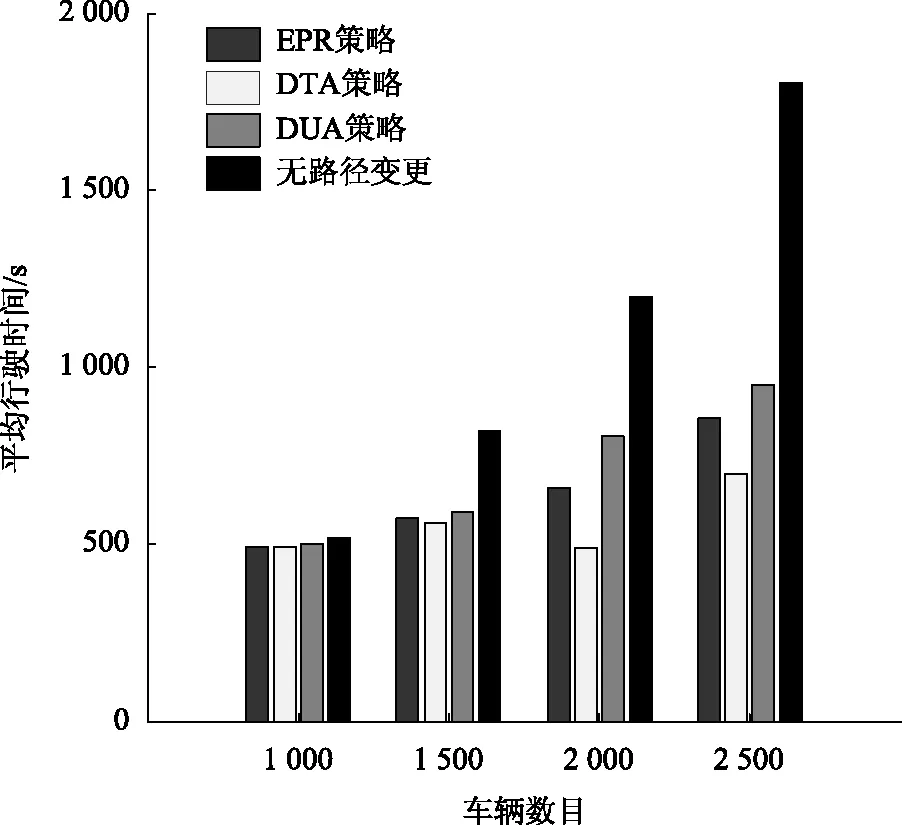
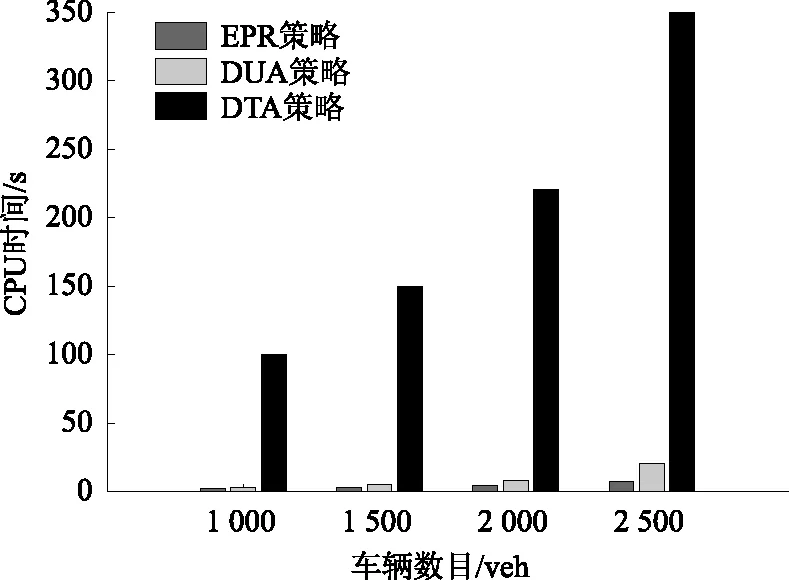
令d(v,w,t)为在时间t出发从点v到点w的最短行驶时间;令L为路网中的节点集合,且l∈L;令Tl={t1,t2,…,tp}为在节点l处的p个时间采样点,且t1 (2) (3) 式中,ti为在节点vi处的时间;e(vi,vj)为路段e,其中,vi和vj为连接路段e的两个交叉口,且vi≠vj;r(l,k)为当次出行中从点l去往点k的无环路径集合。vi至vj路段的预测有效性消散率为: (4) 式中,ε为预测有效性的消散比例,考虑未来过远时间的交通流随机性较大,因此预测的精度会随时间的增长而降低,为确保采用的预测信息是有效的,本研究将消散率分为3个阶段;第1阶段为时间δ内(处在vi处时间为δ),因为可以保证足够预测精度,完全采用预测信息计算行驶时间;第2阶段为时间δ到预测时间段t1内,采用平均速度预测与历史信息结合协同计算行驶时间;第3阶段预测时间段之后,由于预测精度不高,完全根据历史信息计算行驶时间。结合预测信息的评估函数h(v,t)表示为: (5) 其中 (6) 表示在时间t之前从l到v的最近出发采样时间点。 由评估函数h(v,t)的定义可得,h(d,t)≡0,h≥0。下面证明改进A*算法能找到最优解的充分条件,即评估函数需满足FIFO准则以及三角条件。 定理1式(5)、式(6)表示的评估函数符合FIFO准则,同时符合三角条件。 (7) 显然,为了证明t1+h(k,t1)≤t2+h(k,t2),只需证明下面的不等式 (8) 三角条件:给定任意路段e(v,w),在时间节点t,要证明h(v,t)≤ce(t)+h(w,t+ce(t)),令tw=t+ce(t),则等价于证明 t+h(v,t)≤tw+h(w,tw), (9) (10) 显然,为了证明式(9),只需证明 (11) 证毕 当最优路径发生突发拥堵时,为避免发生路径诱导导致的“移堵”现象,本研究为被选车辆分别在各自前k条次优路径中按一定概率随机地分配路线。路径诱导的诱导效率很大程度上受用户的服从率影响,而当用户拥有良好的体验时,其服从路径诱导方案的意愿更强烈,因此本研究在选择概率中加入用户对拥堵的感知因素,从提高用户体验层面出发,制定路径诱导策略。 (12) (13) (14) 道路拥堵状况给不同行程的用户带来的心理感知不尽相同,例如,即将到达终点的用户相对于处在行程起始阶段的用户其紧急程度存在差异,相应地,对拥堵的感知也互不相同。本研究考虑令更紧急的用户以更高的概率选择较快捷路线,从而提高全体用户的整体体验,特引入2种“紧急函数”以表示用户紧急程度: 绝对紧急函数:ACI=RemTT-RFFTT, 相对紧急函数:RCI=ACI/RFFTT。 其中,RemTT为拥堵出现后原始行程剩余行驶时间;RFFTT为无拥堵下原始行程剩余行驶时间;ACI为受拥堵影响距终点需额外花费的时间(即用户的直接紧急程度);RCI为受拥堵影响距终点需额外花费的时间与原始行程中剩余路程所需时间比值(用户的间接紧急程度)。 (15) 式中RCIn为用户车辆Vn的相对紧急程度系数。 (16) 为了更清晰地描述路径分配流程,诱导过程所处路网如图2所示。 图2 诱导过程所处路网Fig.2 Road network in guidance process 当用户车辆V5被选中更改路线,假设p6,5→p5,8→p8,7→p7,4为第1最短路线,车辆V5选择该路线增加的感知效用为: (17) 假设p6, 5→p5, 2→p2, 1→p1, 4为第2最短路线,车辆V5选择该路线增加的感知效用为: (18) 由于路段Pc出现拥堵,包含该路段的行程行驶时间极易更高,但在路径分配时,Pc仍有机会包含在备选路线中并依据分配模型参与选择过程,当Pc处于较拥堵的交通状况时,备选路线中更可能排除Pc,纵然存在包含Pc的路线,车辆被分配到该路线的可能性也较低。但是当Pc处仅是微弱拥堵时,那么备选路线包含Pc甚至被分配到该路线的可能性就比较高,这种情况下若禁止交通在Pc处通行也将浪费交通资源。 假设路网区域G,原始路线H′,拥堵阈值为δ,在当前时刻t,车辆选择系数l,替换路径数量为k,实施过程如下: (2)若#Pcon>0,选择其中预测信息显示最拥堵的路段p∈Pcon; (3)寻找与路段p相距l的近邻路段Pnei,同时找出位于路段p′(p′∈Pnei)且原始路线包含路段p的车辆,所有选中车辆表示为Ω; (4)根据2.1节中改进A*算法为车辆集合Ω中的车辆vn(vn∈Ω)计算前k条最短路线H=[h1,h2,…,hk]; (7)令hi作为车辆vn的新路线,按顺序为选中车辆分配hi; (8)更新路网信息,将已讨论路段从集合Pcon剔除,即Pcon∶Pcon=Pcon-p; (9)当讨论完成全部拥堵路段后(#Pcon==0),得到新路网G。 总的EPR流程如图3所示。 图3 基于用户紧急程度的在途诱导方案流程Fig.3 Flowchart of en-route guidance scheme based on user urgency 试验以SUMO15.0作为仿真服务器,通过SUMO可以实现城市交通的微观模拟以及在线交互等功能。在SUMO平台对拥堵控制诱导策略进行仿真的流程如图4所示。 图4 诱导方案仿真流程Fig.4 Simulation process of guidance scheme 仿真开始前,从OpenStreetMap中下载1个OSM格式的地图,本研究以秦皇岛市某区部分区域为背景,其路网结构如图5所示。 图5 路网结构实例Fig.5 Examples of road network SUMO本身无法处理.osm文件,需要SUMO自带的Netconvert转换格式,同时通过Netedit对生成的net路网作进一步处理,比如移除非机动车、轻轨轨道等,最后,使用Trafficmodeler生成车辆轨迹。路网性质设定如表1所示。 路网设置完成后开始对策略仿真、分析。突发拥堵的程度受造成拥堵的事件类型影响,通常按大小将事件划分为4个级别,本研究分别为各级别事件设定相应的仿真环境,如表2所示。 表1 仿真路网特性Tab.1 Characteristics of simulated road network 表2 仿真环境设置Tab.2 Settings of simulation environment 为确保对诱导策略的机制效果作准确的评估分析,本研究选择3种具有不同评估方向的评估指标:(1)到达车辆平均行驶时间。反应全区域路网的交通运行情况,可以实时评估突发拥堵的动态诱导成效。(2)拥堵路段数量。从全局角度直观地显示诱导成效。(3)用户完成行程数目。从用户立场评估诱导策略,完善评价体系。 对EPR诱导效果仿真过程中,采用Webster周期公式设置信号灯配时。设置5个突发事件点,发生路段(均为路段中)、事件程度随机选择。出于比较分析的原因,事件发生时间均设定为仿真开始后第200 s。经过反复大量试验,得到EPR相关参数设定如表3所示。 表3 EPR相关参数Tab.3 Parameters of EPR (1)用户服从率对EPR的作用。试验构建了4种具有不同车流量的环境,分别在各环境中仿真了EPR在不同用户服从率下的诱导成效,并通过平均行驶时间进行衡量,仿真结果如图6所示。 图6 服从率对诱导效果的作用Fig.6 Influence of compliance rate on guidance effect 由图6可以看出,相对于无任何路径诱导(以服从率为0表示),任何服从率下的EPR诱导策略均能够减少用户的平均行驶时间,并且提高用户服从率能够更显著减少用户的平均行驶时间,提高诱导效率。 (2)EPR的诱导效率评估。仿真试验设置服从率为70%,交通流量水平为2 000,分别从拥堵路段数量、到达车辆数量两方面对EPR诱导成效进行评估,并与DTA策略[17]、DUA策略[18]以及无路径诱导干预的原始交通状态作比较,其中,DUA策略采用的实时信息通过仿真实时获取(非预测信息)。试验结果如图7所示,图7(a)为4种作用方式下拥堵路段数量随时间的增减过程,图7(b)为4种作用方式下到达车辆数量增减过程。 图7 仿真过程中的评估指标Fig.7 Evaluation indicators during simulation process 图7显示,无路径诱导干预的原始交通中,突发事件发生后事件路段开始发生拥堵,并且拥堵迅速向其他路段蔓延,拥堵持续较长时间后逐渐显现消退迹象。对于有路径诱导干预的几种作用方式,EPR策略及DUA策略下,突发事件造成事件路段出现拥堵,但由于两种策略为用户车辆提供了较科学的路径选择信息,避免了信息不对称造成的拥堵蔓延。相对于DUA策略,EPR策略以更快的速度诱导疏散了拥堵车辆,由于其利用了预测的路段速度进行路径寻优,有效防止了车辆转移至相对延迟拥堵的路线,而DUA完全依赖检测的实时数据作出决策,造成了移堵。DTA在抑制拥堵扩散方面缺少优势,但可以较好地调控整体路网的交通均衡状态。在不同车流量下,对EPR策略与DTA策略、DUA策略以及无路径诱导干预的原始交通进行仿真,几种作用方式下的到达车辆平均行驶时间对比结果如图8所示。 图8 不同交通流量的平均行驶时间Fig.8 Mean travel time under different traffic volumes 图8显示,在低车流量下,EPR策略诱导效果最佳,在高车流量下,EPR诱导成效稍逊于DTA,优于DUA并且明显优于无诱导干预的原始交通。 (3)EPR时效性评估。在途路径诱导系统根据动态的交通状态为用户提供路径选择信息,对时效性要求较高,仿真试验通过对事件发生后600 s内EPR策略更新所需CPU时间的平均值对其时效性进行评估,并与其他两种策略作对比,不同车流量下几种策略的平均CPU时间如图9所示。 图9 不同车流量下的CPU时间Fig.9 CPU time for different traffic volumes 图9显示,EPR策略更新的平均CPU时间在3种策略中最少,DTA以系统最优的均衡状态为路径分配准则,趋于理想化,时效性最差,DUA选取常见的最短路径寻优方式,代表了当前大多数诱导系统的时效性,因为EPR差别化计算最短路径,且选择搜索效率优异的改进A*算法,因此时效性高于DUA。 突发拥堵的突发性及随机性使用户无法在出发前做出路径选择,当最优路径被预测出发生突发拥堵时,为避免发生路径诱导导致的“移堵”现象,本研究为被选车辆分别在各自前k条次优路径中按一定概率随机地分配路线。为提高用户对诱导方案的服从率进而提升诱导效率。本研究在备选路线随机均衡选择模型中加入用户对拥堵的感知因素,提出了以感知拥堵作为路径诱导的路径分配限制因素,并构建了行驶时间感知效用算法。同时,通过改进A*算法估价函数中的评估函数,将路段平均速度预测与历史平均回归模型结合计算行程时间,从而实现了考虑时间依赖性的实时最短路径寻优。仿真结果表明,提高用户的诱导服从率有助于提升突发拥堵下的诱导疏散效率。诱导疏散效果与现有几种算法相比,所提在途路径诱导策略在兼顾计算效率前提下,在不同车流量水平下,均可以为用户车辆提供较科学的路径选择信息,避免信息不对称造成的拥堵蔓延,同时,由于其利用了预测的路段速度进行路径寻优,进而避免了移堵现象的发生。 本研究提出的路径诱导策略以预测模型得到的预测信息作为诱导依据之一,如何利用当前研究热点车联网技术实现的车车通信、车路通信所产生的共享信息,实现近似路网均衡的路径诱导策略是一个应用型很强的研究方向。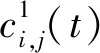
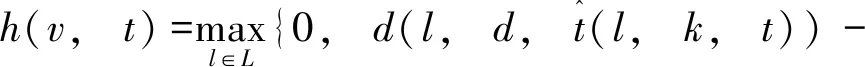
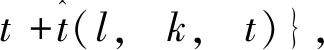
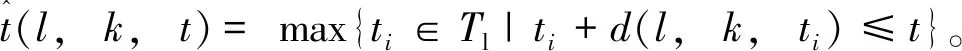
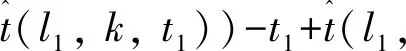
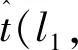
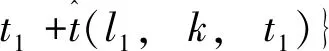

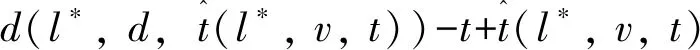
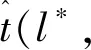
1.2 考虑用户紧急程度的路径分配模型

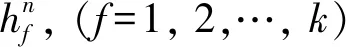
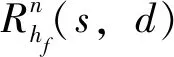
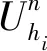
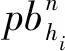
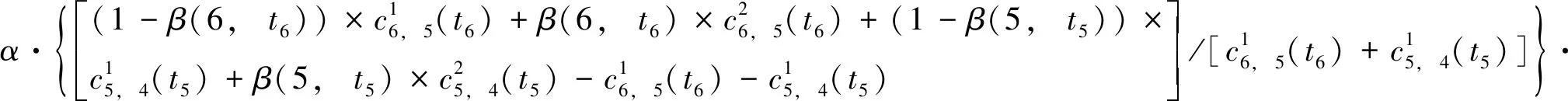
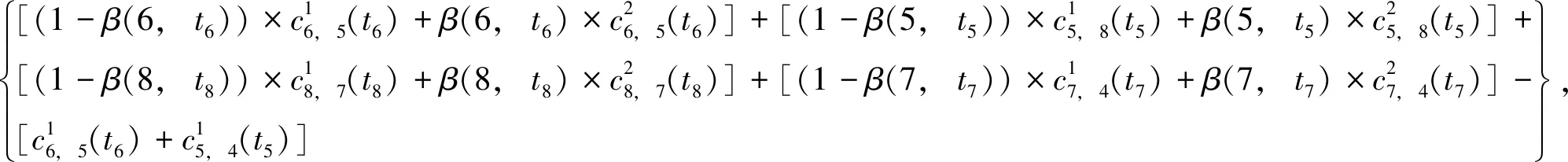
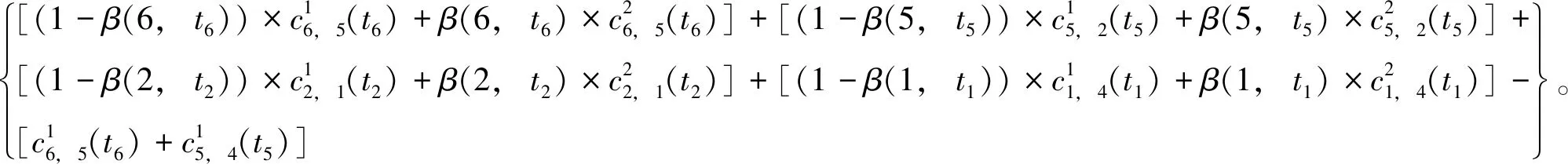
1.3 考虑用户紧急程度的在途路径诱导方案实施过程
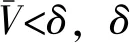
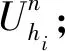
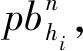
2 算例分析
2.1 试验设置



2.2 仿真评估结果及分析

3 结论

