栓接U肋钢箱梁考虑对接偏差的疲劳性能及改进方法研究

李传习，冯 峥，王文强，陈卓异，柯 璐

(1.长沙理工大学 桥梁工程安全控制教育部重点实验室，湖南 长沙 410004； 2.佛山市路桥建设有限公司，广东 佛山 528303)

0 引言

正交异性钢桥面板疲劳开裂是该类钢桥使用一段时间后常出现的问题[1-2]，U肋纵向对接接头部位是其疲劳易损部位之一[3-8]。早期钢箱梁面板U肋对接往往采用嵌补段焊接连接，因衬垫板与U肋壁板不密贴、定位点焊下锈蚀不易清除、对中偏差、仰焊焊接质量不容易保证等，多座桥梁在该焊缝部位出现较为严重的疲劳开裂问题[8-11]。文献[8]认为解决闭口纵肋焊接接头疲劳问题最好的方法就是面板焊接、纵肋高强螺栓连接(即栓接U肋)。近些年，欧美等应用正交异性钢箱梁技术比较成熟的国家也开始采用这一连接方式[12]。我国在南京二桥首次采用了栓焊连接[13]，随着认识的加深，栓焊连接得到了国内越来越多的专家学者认可，被应用于杭州湾跨海大桥[14]、港珠澳大桥[4,7]、沱江四桥等新修建的大跨度桥梁中。

虽然，文献[15]对无对接偏差的正交异性桥面板栓焊接头的疲劳性能进行了研究，发现拼接板是其受力的薄弱环节，易在内侧拼接板中间区域下缘产生疲劳裂纹，但尚未有文献比较或者深入比较正交异性桥面板栓焊接头与全焊接头的疲劳性能。

由于任一U肋纵轴线的平面位置受定位精度和焊接变形的影响，相邻节段钢箱梁面板U肋往往会存在水平面内对接位置偏差(本研究简称对接偏差)。尽管工厂制造普遍采用自动化、智能化、模块化的生产方式，但由于下料环境温度、焊接残余变形等影响，钢箱梁节段施工现场对接仍不时出现1～6 mm 的对接偏差，某新建斜拉桥最大偏差甚至达到了9 mm。该偏差必然引起轮载应力改变。文献[16]对具有对接偏差的全焊接头(非栓焊接头)进行了研究，发现纵肋对接偏差与焊接质量相比对其疲劳性能的影响更不利。

根据规范[17]要求，采用栓接方式的U肋对接偏差超过3 mm时，需要根据实际测量的偏差尺寸，在栓接的U肋侧边加设填充钢板，才能使用钢板进行拼接。而该种连接方法产生的疲劳问题相关规范还未明确说明[17-19]，有关研究还未涉及。

相关规范已在大量疲劳试验与实桥疲劳相关信息汇集的基础上，给出了相应细节的疲劳寿命曲线[18-19]。在疲劳寿命曲线已知和车辆荷载(含作用次数)一定的情况下，正交异性桥面板各细节的疲劳主要与不利轮载应力的大小(因这些细节影响线短，不利轮载应力值即为应力幅[5])有关。因此，结合已有的疲劳寿命曲线(规范给出)，通过不同对接偏差下U肋栓接邻近区和无对接偏差下非栓接邻近区的不利轮载应力(即疲劳应力)分析，可考察相应疲劳性能或其优劣(亦即相应疲劳寿命的长短)。

本研究以某大桥为工程背景，利用ABAQUS分析上述不利轮载应力，并考察相关疲劳性能及影响，并研究改进措施。

1 工程概况

2016年通车的佛山某独塔斜拉桥跨径布置为(135+260)m，双向八车道，主梁钢箱梁采用PK型断面，材料为Q345qc钢材。标准断面高3.58 m，宽40.54 m，顶板厚16 mm，底板厚14 mm，横隔板厚12 mm，加强横隔板厚16 mm，中纵腹板厚 14 mm，边纵腹板厚14 mm，横隔板间距为3 m。纵向U肋断面为300 mm×280 mm×8 mm，中心距为 600 mm，标准断面如图1所示。钢箱梁段对接处所在横截面距相邻横隔板均为1.5 m。钢箱梁段之间采用栓焊连接(参见图2)，即：除顶板U肋采用拼接板栓接连接，梁段其余连接均为焊接。U肋对接间距16 mm。拼接板设计尺寸为536 mm(长)×180 mm(宽)×12 mm(厚)，选用Q345qc钢材。连接用螺栓采用M22摩擦型高强螺栓，性能等级为10.9 S，螺栓孔直径为24 mm，螺栓预紧力为190 kN。

图1 钢箱梁标准断面图(单位:mm)Fig.1 Standard cross-section of steel box girder(unit:mm)

该桥相邻钢箱梁节段连接安装时，顶板U肋对接部位出现了水平面内的位置偏差，偏差1～6 mm的现象比较普遍，个别点偏差达9 mm，如图2(a)所示。为此，施工方提出并经设计、监理等建桥各方参与的专家咨询会认可的处理方案。该方案的拼接板设计尺寸均保持不变，对于偏差1～3 mm的部位，按规范[17]采用通过螺栓拧紧强制矫正进行连接(简称拼接板设计尺寸的强制矫正方案)，见图2(b)；对于偏差超过3 mm的部位，在U肋内外表面使用材质相同尺寸为260 mm(长)×180 mm(宽)的钢板进行填充(填充板厚度据偏差大小而定)，填充后再用拼接板进行连接(见图3)(简称拼接板设计尺寸的填充板方案)；当偏差等于3 mm时，既可采用拼接板设计尺寸的强制矫正方案，也可采用拼接板设计尺寸的填充板方案。因上述3种情况拼接板均采用原设计尺寸，故处理方案统称为拼接板设计尺寸的处理方案。

图2 U肋错位情况及强制矫正方案示意图Fig.2 Schematic diagram of U-rib dislocation and compulsory corrective scheme

为方便表述各拼接板的疲劳应力差异，将拼接板从左至右依次编号为PJB-1～PJB-4(见图4)。

2 拼接板设计尺寸方案的有限元模型及加载方式

2.1 有限元模型

为了分析栓接U肋处U肋腹板及拼接板的轮载应力，选取标准断面长12 m的梁段(一端距离U肋对接位置4.5 m，另一端距离U肋对接位置7.5 m)进行有限元分析。边界条件为约束钢箱梁两端，一端约束节点DX，DY，DZ3个方向平动自由度，另一端仅约束节点竖向位移。有限元分析采用以下假定：(1)板件处于弹性范围，不考虑其材料非线性和几何非线性；(2)焊缝部位材料的物理特性与母材相同；(3)不考虑螺栓松动滑移。

图3 U肋对接偏差填充板方案示意图Fig.3 Schematic diagram of filler plate scheme for connection deviation of U-ribs

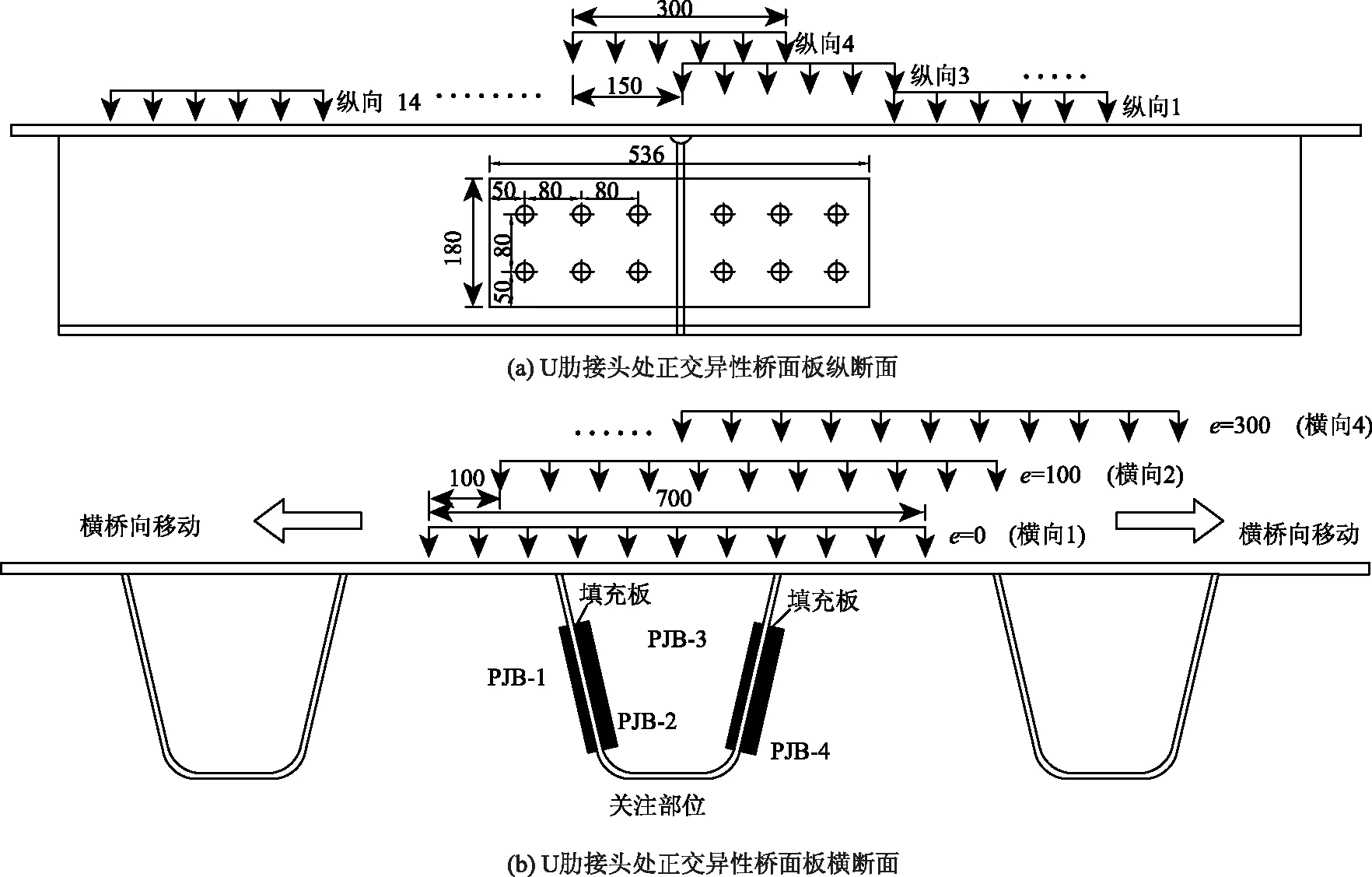
图4 拼接方式及纵横向加载位置(单位：mm)Fig.4 Connection method and longitudinal and lateral loading positions (unit:mm)

针对顶板U肋的对接偏差情况，建立6组有限元模型，即模型Ⅰ～Ⅵ。模型Ⅰ～Ⅴ分别对应U肋对接偏差9 mm(最大偏差情况)、偏差6 mm、偏差4 mm、偏差3 mm及偏差0 mm(未偏差)的拼接板设计尺寸的填充板方案(偏差为0时，填充板厚度为0，即无填充板)，模型Ⅵ对应偏差 3 mm 的拼接板设计尺寸的强制矫正方案。各有限元模型的单元类型、单元尺寸以及接触面模拟方式如下：

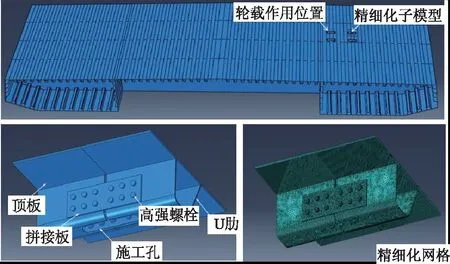
图5 钢箱梁有限元模型Fig.5 Finite element model of steel box girder

梁段非关注部位采用S4R壳单元(图5)，整体网格尺寸为300 mm；为了得到关注部位的精确应力幅，在各模型U肋对接部位前后各取500 mm建立精细化子模型，其中U肋、顶板、填充钢板及拼接板采用C3D8R实体单元，网格尺寸细化为3 mm，并保证各板件沿板厚方向至少具有3层网格，螺栓尺寸划分为2 mm，网格层数根据螺栓长度而定；板壳单元与实体单元之间通过共节点的方式相连，并设置适宜的网格尺寸使二者连接平顺，协调受力。拼接板与U肋腹板之间、填充板与U肋腹板之间通过Interaction模块中surfuce to surfuce contact(standard)方式模拟接触问题，即接触面切线方向采用库伦摩擦，摩擦系数取0.45，法向方向为硬接触，螺栓预紧力通过螺栓单元截面力施加。因摩擦型螺栓连接界面间不容许有滑移[17]，且板厚较小，故将所有螺栓与拼接板之间、填充板与拼接板之间的接触方式简化为节点耦合方式模拟(计算规模相对较小)。

按上述划分和选取方式所得模型Ⅰ～Ⅵ的节点总数分别为1 231 991，1 129 624，1 012 645，975 251，959 859， 965 262；单元总数分别为1 045 135，949 190，853 573，824 529，798 758，785 296；其中C3D8R单元数分别为889 531，786 401，684 025，665 231，648 052，652 984。

2.2 加载方式

桥梁结构的疲劳损伤与应力幅大小有关，而应力幅主要由车辆荷载引起。研究表明[20]，正交异性钢桥面板在轮载作用下，其荷载效应是局部的，关键部位的应力影响线较短。因此本模型仅需考虑2轴、4个轮载的作用。采用《公路钢结构桥梁设计规范 JTG D64—2015》(简称《公路钢桥规》，下同)的单车疲劳荷载模型(图6)计算疲劳易损细节的应力幅。标准疲劳车轴重120 kN，单轮重为60 kN，按45°扩散角考虑铺装层荷载扩散效应，扩散后轮载作用范围为0.7 m×0.3 m，横向轮距2.0 m，轴距1.2 m。

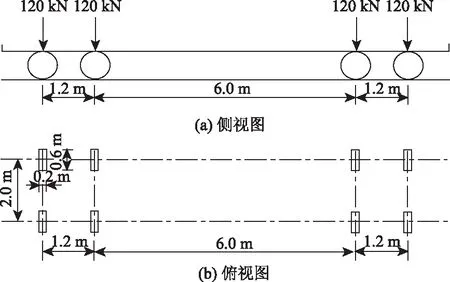
图6 《公路钢桥规》疲劳荷载模型ⅢFig.6 fatigue load model Ⅲ in Specifications for Design of Highway Steel Bridge

为了得到考察对象的最不利加载位置，车轮加载时，车轮横向位置有7种，即轮载中轴线位于被考察栓接U肋正上方(见图4(b))，为横向位置1(e=0)，以此为基准往横桥向左右分别移动100，200，300 mm，即得到车轮另外6个横向位置(由于4块拼接板之间有一定的间距，为了得到各拼接板应力变化历程，比规范[19]多增加了2个位置)。如图4(b)所示，车轮向左移e为负、右移为正，当e=-100～-300 mm 时加载位置分别命名为横向5～横向7。车轮的纵向位置有14种情况(如图4(a))所示，即纵向1～10以150 mm为间距进行移动，纵向11～14以300 mm 为间距进行移动。其中，纵向4位于栓接U肋正上方。计算工况包括纵向位置4时的各横向位置工况(共7个)，其他纵向位置时的e=0,±100，±200 mm各横向位置工况共13×5=65个。

3 拼接板设计尺寸处理方案的栓接U肋轮载应力及抗疲劳能力

计算所得各工况的U肋及拼接板的应力结果表明，横向1(e=0)、纵向4为最不利加载位置(车轮作用在U肋对接接头正上方)。下面给出的均是车轮荷载位于横向1、纵向4的相应计算结果。

3.1 轮载应力最不利位置与等效应力幅

限于篇幅，仅以模型Ⅱ为例说明栓接接头应力分布最不利受力位置及等效应力幅。图7给出了栓接处U肋腹板最不利层(即最内层)及拼接板最不利层(即与腹板紧邻的层)的应力云图，其中图7(a)表示U肋腹板应力分布，图7(b)以PJB-2为代表表示拼接板部位的应力分布(图中拼接板左侧部位与U肋腹板直接相连，右侧部位通过填充板与U肋腹板相连)。

图7 模型Ⅱ(偏差6 mm)各构造细节应力云图(单位:MPa)Fig.7 Stress nephograms of structural details in model Ⅱ(6 mm deviation)(unit:MPa)

在图7(a)中U肋腹板最大主拉应力(也是正应力，下同，略)为42.8 MPa，在图7(b)中拼接板最大主拉应力为63.5 MPa，主应力方向近似沿纵桥向方向。由图7(a)还可见，U肋腹板上应力集中分布在U肋与拼接板接触边缘处以及下缘内侧两螺栓孔中间区域，应力极大值出现在与拼接板下缘尖角接触部位。由于二者差值较大，栓接处U肋腹板应力不再关注。4块拼接板中内侧拼接板最不利应力要大于外侧，且在PJB-2处达到最大值。图8给出了拼接板(PJB-2)下缘内侧的应力分布情况。图中横坐标表示拼接板底缘的纵向位置，由左端点往右端点递增，其中0,536 mm分别表示拼接板的左右端点；50，130，210，326，406，486 mm分别对应各高强螺栓轴心位置；268 mm表示拼接板底缘中点。

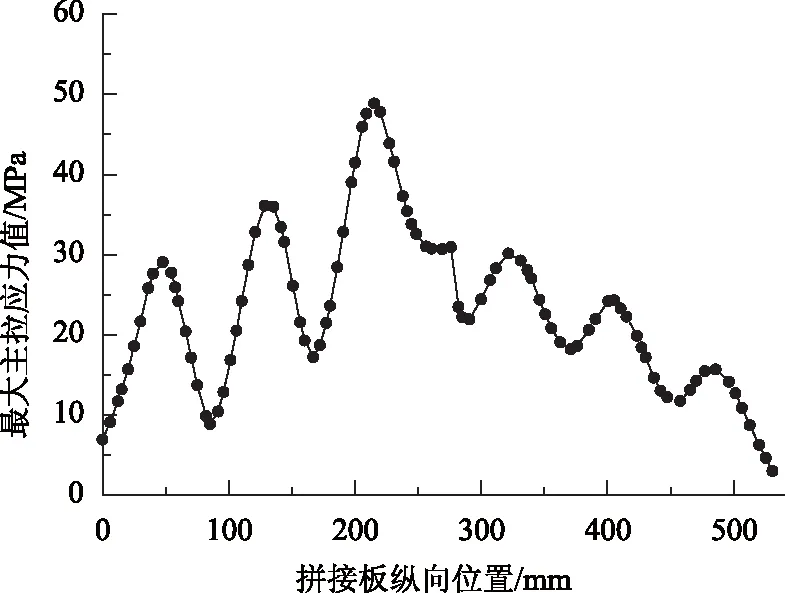
图8 模型Ⅱ拼接板纵向应力分布情况Fig.8 Longitudinal stress distribution of splice plate in model Ⅱ

从应力变化曲线可以看出：拼接板应力值较大区域集中在各螺栓孔附近，且在无填充板侧紧靠接头第一排螺栓孔附近应力达到最大值(不利点)；整体上应力分布纵向由中间向两边递减，且左侧(无填充板)应力峰值大于右侧(有填充板侧)，有填充板的右侧拼接板相当于增加了自身厚度，厚度的增加降低了拼接板应力幅水平。

车轮纵向位置位于纵向4，横向位置分别为横向1～横向7时的U肋、4块拼接板各自不利点的主拉应力见图9。

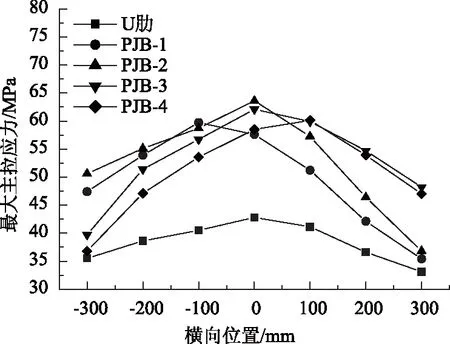
图9 模型Ⅱ U肋及拼接板在轮载横向作用下最大主拉应力Fig.9 Maximum principal tensile stresses of U-rib and splice plates under transverse wheel load in model Ⅱ

根据Miner线性累积损伤准则，考虑轮载横向分布概率，可得出U肋及拼接板的等效应力幅ΔσE。限于篇幅，在此仅以PJB-2为例进行说明。计算公式参见《公路钢桥规》[19]。

(1)

式中，ΔσPJB-2为PJB-2处的等效应力幅；Pi为车轮横向位置概率分布系数；Δσi为各横向位置关注部位的最大主拉应力值。

模型Ⅰ，Ⅲ，Ⅳ，Ⅵ的最不利轮载应力位置及各关注部位沿纵桥向的应力分布情况与模型Ⅱ相似。其中模型Ⅴ因无填充板而结构对称，应力分布亦对称。

3.2 各模型最不利工况轮载最大主应力

各模型U肋及拼接板最不利工况(横向1，纵向4)的最大主拉应力值见表1，模型Ⅰ～模型Ⅴ各构造细节随对接偏差程度的应力变化曲线见图10。

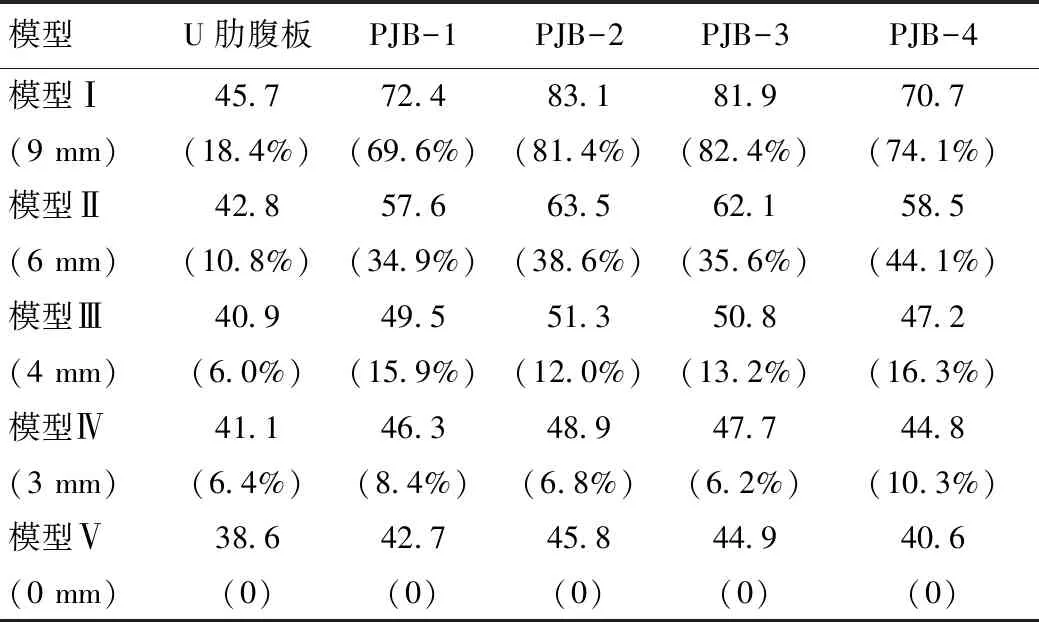
表1 各模型U肋栓接接头构造细节最大主应力情况(单位：MPa)Tab.1 Maximum stresses of structural details of bolted U-rib joint in each model(unit: MPa)

注： 表中括号内数值表示各模型相对于模型Ⅴ的最大主应力增长情况。

由表1可见，U肋对接偏差9 mm，较未偏差情况下U肋腹板应力值增加了7.1 MPa。其原因为对接偏差过大，使力流不顺畅，造成U肋与拼接板接触边缘应力增大。

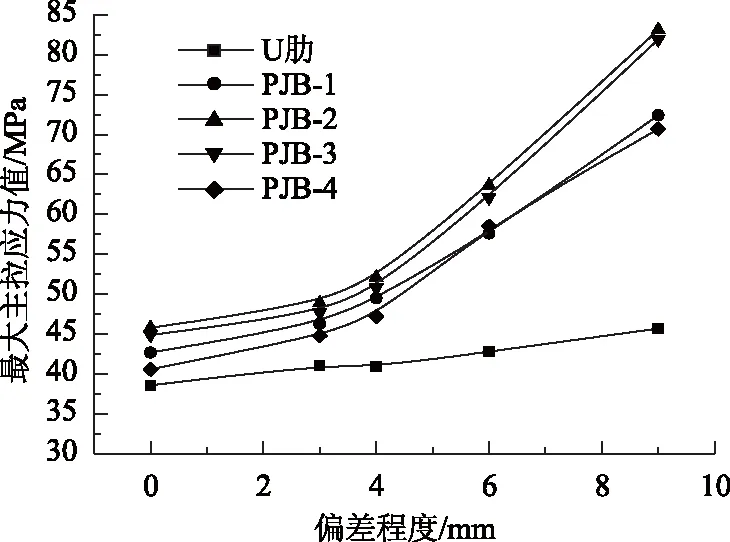
图10 各构造细节随U肋偏差程度应力变化曲线Fig.10 Curves of stress of structural details vs. of U-rib connection deviation

由图10可见，各拼接板最大应力远大于U肋腹板。当对接偏差9 mm时，受力最不利的拼接板(PJB-2)的最大主拉应力值为83.1 MPa，最大主拉应力值较未出现偏差时的45.8 MPa增大了81.4%；偏差6 mm 时，最大主拉应力值63.5 MPa较未出现偏差时的值增大了38.6%；偏差3 mm(填充板方案)时的最大主拉应力值48.9 MPa较未出现偏差时的值增大6.8%。随偏差增大，各拼接板和U肋腹板不利点应力增大。当U肋偏差在3 mm以下时，U肋及拼接板的应力值增长缓慢，当偏差超过3 mm时，拼接板应力值随偏差增大呈非线性急剧上升。

3 mm偏差的填充板方案(即模型Ⅳ)U肋腹板最大主拉应力为41.1 MPa，拼接板最大主拉应力为48.9 MPa；3 mm偏差的强制矫正方案(即模型Ⅵ)U肋腹板最大主拉应力为41.8 MPa，拼接板最大主拉应力为50.2 MPa。在两种方案连接下，U肋主应力分布及大小几乎一致，采用强制矫正方案的拼接板主应力值要略大于设填充板的方案，但相差不超过3%。考虑到填充板方案相对工艺较多，耗材较大，水平对接偏差1～3 mm的部位采用强制矫正的方案更为合理。

3.3 基于《公路钢结构桥梁设计规范》(JTG D64—2015)的疲劳验算

基于《公路钢桥规》的U肋及拼接板的抗疲劳验算公式为：

(2)

式中,γFf为疲劳荷载分项系数(取1)；Δφ为放大系数(取0)；Δσc为疲劳细节类别，即200万次的疲劳强度(200万次的容许疲劳应力幅)(采用摩擦型高强度螺栓连接的双面对接接头，据《公路钢桥规》附录C，其值为110 MPa)；ΔσE2为按200万次常幅疲劳循环换算得到的等效应力幅；γ为等效损伤系数γ=γ1γ2γ3γ4(按《公路钢桥规》考虑损伤效应系数、交通流量系数、设计寿命影响系数、多车道效应系数后，本计算γ取值为2)；σpmax，σpmin分别为疲劳荷载模型最不利加载的最大和最小正应力；ks为尺寸效应折减系数(取1)；γMf为疲劳抗力分项系数(取1.15)。

考虑轮载横向位置的概率分布，按《公路钢桥规》5.5.7条(参考见式(1))得到各模型最不利拼接板(PJB-2，见图4)、U肋腹板最大应力的等效应力(幅)ΔσE(见表2)。由式(2)检算其抗疲劳的富余量，并按规范5.5.8条检算其疲劳寿命。式(2)两边相等时的疲劳寿命按100 a计，则式(2)左边等于(ksΔσD)/γMf时的疲劳寿命为250 a(100 a×500万次/200万次=250 a；常幅疲劳极限ΔσD为500万次的疲劳强度)，当γFfΔσE2大于(ksΔσD)/γMf时，参见《公路钢桥规》5.5.8条，寿命与应力幅比值3次方成反比，即：

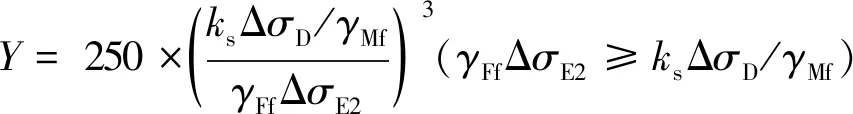
(3)

当γFfΔσE2小于(ksΔσD)/γMf时，寿命与应力幅5次方成反比，即：

(4)

计算结果见表2。

从表2结果可以看出，U肋对接偏差在4 mm以内时，U肋腹板及拼接板的疲劳应力幅均满足《公路钢桥规》中的疲劳强度要求，疲劳寿命接近或超过设计寿命。偏差程度超过4 mm时，U肋腹板应力幅能满足规范要求，但拼接板疲劳应力幅不满足要求，与规范标准差距较大(最大相差63.8%)，特别是偏差9 mm时，其预测疲劳寿命仅22.7 a，远未及设计要求。

4 非栓接邻近区顶板U肋轮载应力及不同连接方式下U肋疲劳性能比较

U肋连接方式主要有嵌补段焊接连接和高强螺栓连接。显然，在车辆荷载(含作用次数)完全相同情况下，其抗疲劳性能或者其优劣(或者疲劳寿命)可根据“应强比”，即轮载等效应力幅与常幅疲劳极限比值(ΔσE/ΔσD)的大小来判断。“应强比”越小，相应连接方式的抗疲劳性能越佳。

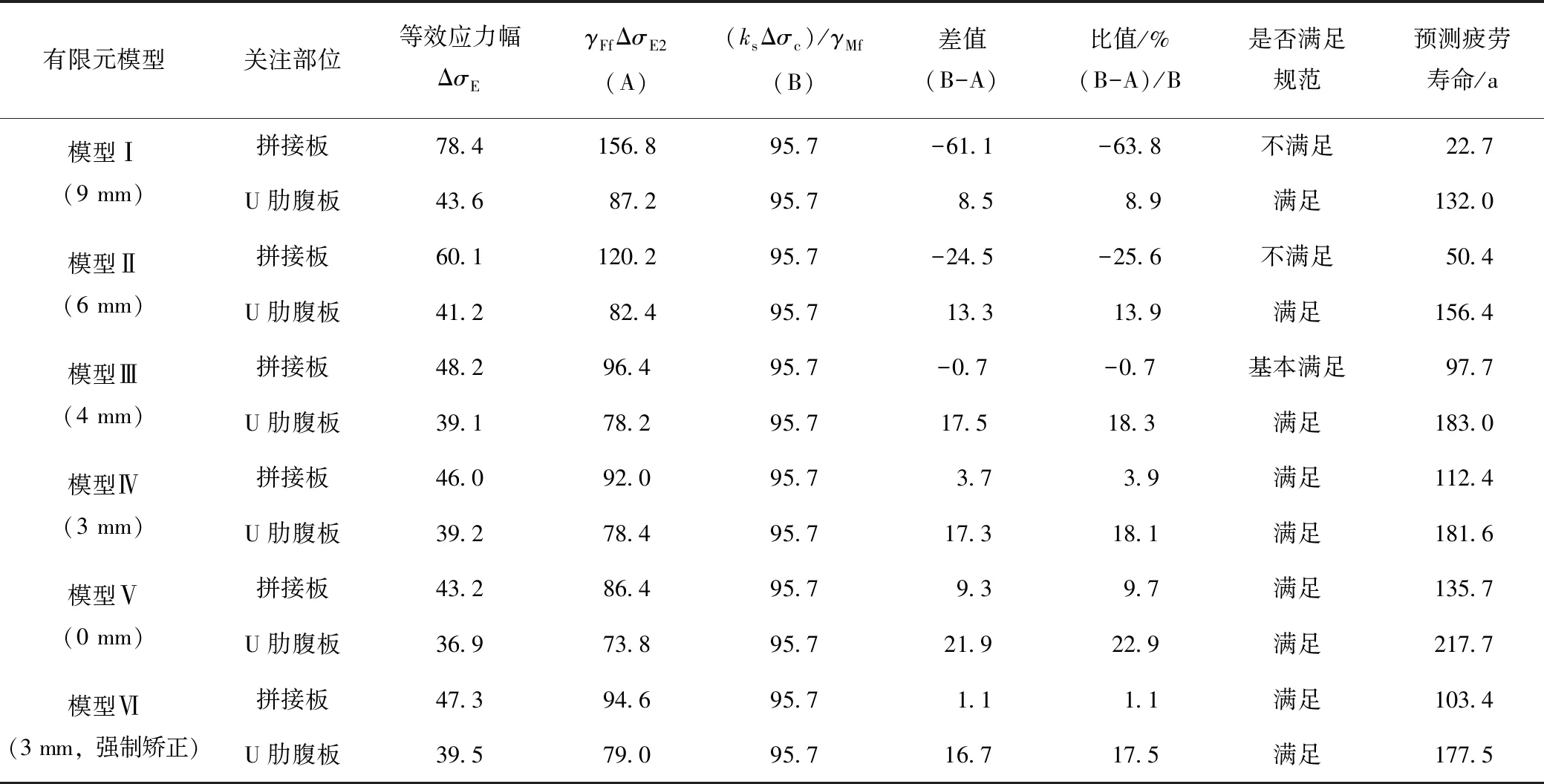
表2 各模型构造细节疲劳强度验算(单位：MPa)Tab.2 Fatigue strength checking of structural details in each model (unit:MPa)

由上文可知，栓接U肋疲劳细节为110，其常幅疲劳极限ΔσD=(2/5)1/3Δσc=81.05 MPa，无对接偏差的栓接U肋(模型Ⅴ)中的U肋腹板的等效应力幅为36.9 MPa，其“应强比”为0.455，拼接板的等效应力幅为43.2 MPa，其“应强比”为0.533。而采用嵌补段焊接连接，根据文献[10]U肋的疲劳强度等级相当于Eurocode规范的71类细节，其常幅疲劳极限为52.3 MPa。对非栓接邻近区U肋(相当于焊接连接U肋的嵌补段，其焊缝质量与母材相同)展开疲劳性能研究，关注部位选取为与图5中模型关注栓接接头纵向中轴线对称的位置。在轮载作用下其U肋腹板的等效应力幅为24.6 MPa，其“应强比”为0.470。相比较而言，栓接U肋“应强比”小于嵌补段U肋，但拼接板的“应强比”要大于嵌补段U肋。在理想状况下(即不考虑对接偏差及焊接缺陷)栓接U肋中的U肋腹板的抗疲劳性能要稍优于嵌补段焊接连接，但拼接板的疲劳寿命低于嵌补段焊接连接。当对接偏差达到或超过6 mm时，背景工程中拼接板疲劳寿命将远低于嵌补段焊接连接U肋。

5 对接偏差较大情况下拼接板尺寸的改进

5.1 增加拼接板宽度

顶板U肋对接偏差使拼接板受力增大，施工手孔削弱了原结构的刚度。对接偏差超过4 mm后，采用尺寸为536 mm(长)×180 mm(宽)×12 mm(厚)的钢板进行拼接，拼接板抗疲劳性能不能满足要求。针对这一情况对原处理方案加以改进。考虑到在U肋腹板内侧施工不便，将模型Ⅰ、模型Ⅱ外侧拼接板的宽度往U肋下缘方向增宽30 mm，而内侧拼接板及填充板尺寸和位置不加以改变(方案A(图11))。改进后模型的单元类型、划分方式、接触面模拟、加载方式等与图5相同，改进后模型Ⅰ单元总数为1 061 913，模型Ⅱ单元总数为968 386，计算结果均收敛良好。

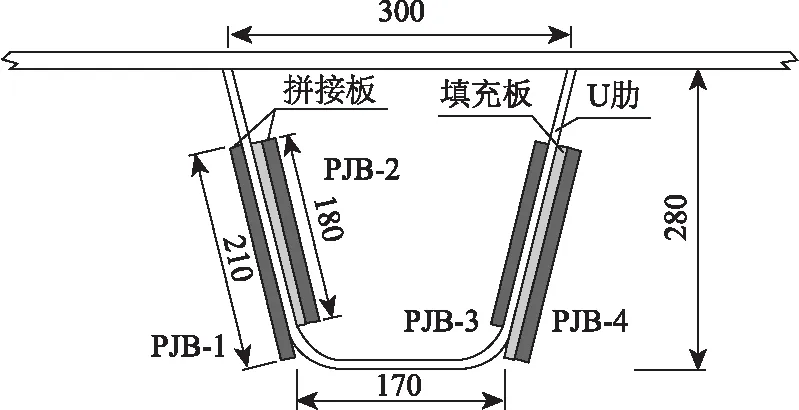
图11 方案A示意图(单位:mm)Fig.11 Schematic diagram of scheme A(unit:mm)

板宽的增加使栓接接头局部区域刚度提高。在该改进方案下，模型Ⅱ拼接板不利点应力峰值由63.5 MPa降为50.3 MPa(等效应力幅由60.1 MPa降为47.1 MPa)，降幅达到20.8%(21.6%)，改进效果明显，按3.3节所述方法进行疲劳强度验算，满足强度要求。模型Ⅰ拼接板不利点应力峰值由改进前的83.1 MPa降为60.9 MPa(等效应力幅由78.4 MPa降为57.9 MPa)，降幅达到了26.7%(26.1%)，但将改进后的等效应力幅代入式(2)进行疲劳强度验算，未满足要求。

5.2 外侧改用L形拼接板

仅加宽外侧拼接板还不足以使偏差程度较大的模型(偏差9 mm)满足抗疲劳设计要求，将模型Ⅰ外侧拼接板改为L形角钢连接，如图12所示(方案B)。进一步改进后的模型Ⅰ的单元类型、划分方式、接触面模拟、加载方式等与图5相同，模型单元总数为1 127 705。

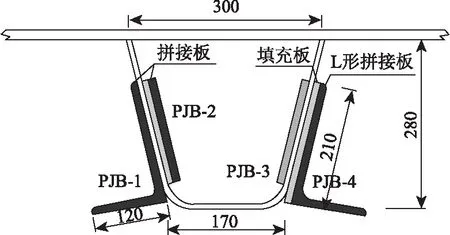
图12 方案B示意图(单位：mm)Fig.12 Schematic diagram of scheme B(unit:mm)

采用“L”形拼接板使结构刚度进一步得到提升，在轮载作用下，拼接板不利点应力峰值由83.1 MPa 降为47.3 MPa(等效应力幅由78.4 MPa降为45.0 MPa)，降幅达到了43.1%(42.6%)，按3.3节所述方法进行疲劳强度验算，其值满足要求。

由疲劳寿命与应力幅的3次方成反比的近似关系，其拼接板疲劳寿命比原方案至少增加5.3倍，超过桥梁设计100 a的寿命要求。因此，外侧采用“L”形角钢连接，可以明显降低栓接接头拼接板应力幅值，大幅降低了结构疲劳开裂风险。

6 结论

(1)栓接U肋中U肋腹板的抗疲劳性能要稍优于嵌补段焊接连接U肋，但其常规设计的拼接板抗疲劳性能不及嵌补段U肋，即使在无对接偏差情况下。

(2)无论是否存在U肋对接偏差，对接偏差连接处理无论采用强制矫正，还是填充板方式，栓接U肋中拼接板的主应力(正应力)最大值均出现在拼接板无填充侧邻近U肋层下缘紧靠接头第一排螺栓孔处，拼接板主应力(正应力)整体上由对接处纵向中点往两端递减；栓接U肋腹板应力集中分布在U肋与拼接板接触边缘及下缘内侧两螺栓孔中间区域，其最大应力出现在与拼接板下缘尖角接触部位。

(3)当U肋对接偏差不超过3 mm时，采用强制矫正方案所得拼接板和U肋腹板的轮载应力与填充板方案差别不大，考虑到强制矫正方案，耗材较省，工艺较少，因此，“当栓接U肋对接偏差不超过3 mm，宜采用强制矫正方式”的规范规定[17]合理。

(4)当拼接板尺寸保持不变，仅改变填充板厚度，以适应不同对接偏差大小时，随对接偏差增大，拼接板及U肋腹板的最大轮载应力增大。当该偏差小于3 mm时，轮载应力随偏差增大增长缓慢，当偏差超过3 mm后，轮载应力呈非线性急剧增加。

(5)对于背景工程，U肋对接偏差4 mm时，可采用拼接板设计尺寸的填充板方案进行栓焊连接；当对接偏差为5～6 mm时，外侧拼接板的宽度加宽至210 mm(厚度12 mm，长度536 mm保持不变)；对接偏差为7～9 mm时，两外侧拼接板应采用536 mm×210 mm×120 mm×12 mm的L形角钢连接，方可满足疲劳寿命验算要求。