机场道面平整度评价指标的相关性分析
凌建明, 刘诗福, 袁 捷, 刘 媚
(1. 同济大学 道路与交通工程教育部重点实验室,上海 201804; 2. 上海市市政规划设计研究院有限公司,上海 200031)
0 引言
在我国机场建设发展迅速的同时,机场道面的检测评价必不可少。不平整的机场道面可能导致飞机构件的疲劳损伤,影响驾驶员对仪器读数。同时也将造成乘客的不舒适,加速机场道面的损坏。因此,机场道面平整度的检测及评估是机场道面评价中必要的内容。在我国《民用机场道面评价管理技术规范》中,规定“道面平整度评价一般采用国际平整度指数(IRI)作为指标;不具备测试条件时,可采用3 m直尺法进行评价,其中IRI以算术平均值分段评价,3 m直尺以最大间隙的平均值进行评价”[1]。由于设备的缺乏,我国早期机场道面检测的历史资料中,多采用3 m直尺法检测道面平整度。但随着激光平整度仪的推广,可方便快速地获取IRI,目前IRI在机场道面平整度评价中的应用也越来越广泛。因此,研究IRI和3 m直尺下最大间隙值的相关关系,可提供一种延续机场道面历史资料信息的有效途径,为机场道面的性能预测提供更多的基础样本,制订更科学合理的道面养护维修对策。
国际平整度指数IRI为基于1/4车模型的反应类平整度指标,于1986年由世界银行在巴西进行道路平整度试验时提出[2]。IRI来自于道路平整度评价,但目前中国、巴西、意大利、墨西哥及南非等国家都直接采用IRI评价跑道或滑行道的评价指标,意大利等国家也间接采用了IRI。然而,ICAO[3]和FAA[4]等认为1/4车难以反映飞机本身的动力学响应。Chen等[5]利用APRAS商业软件研究表明IRI的敏感波长和飞机相差较大。凌建明[6]通过建立飞机的动力学模型研究表明IRI对短波敏感而飞机滑跑对长波敏感。Loprencipe证明了用IRI评价机场跑道可能会得到不正确的维修措施[7]。尽管如此,基于车载式激光断面仪的IRI测量设备在市场上应用广泛,测量跑道或者滑行道的IRI值十分便利,IRI作为间接或辅助的机场道面平整度评价指标仍是趋势[8]。
直尺下最大间隙值是典型的断面类指标,能客观准确地反映平整度情况,是最早使用于评价道路平整度的指标之一。尽管测试效率低,但操作简单、检测方便使得直尺测量法在机场道面平整度评价上应用较多,特别是早期的中小型机场。不过,各个国家和组织采用的直尺长度及控制标准不一样。加拿大交通运输部采用的是4.5 m直尺不超过5 mm[9],ICAO以及我国采用的3 m直尺不超过3 mm[1],FAA对刚性道面采用的是4.88 m不超过6.35 mm,柔性道面是3.66 m不超过6.35 mm[10]。我国民航机场采用的是3 m尺多向检测,包括水泥板的纵向、横向和斜向。考虑到来源数据只有纵向的不平整相对高程,为和道面纵断面的IRI值相对应,本研究分析的3 m直尺最大间隙针对的是道面纵向不平整。
在两个指标的相关性方面多数研究针对的是公路路面,如Peter等[11]通过290条实际路面的纵断面高程,分别建立了沥青路面和水泥混凝土路面下IRI和直尺指标(SE)之间的相关关系。陆键[12]、蔚晓丹[13]通过实测路段数据分析也得到了两者的换算关系。在机场道面方面的研究较少。吴志心[14]以某实测道面数据为输入,结果表明IRI与3 m直尺最大间隙之间不存在显著性差异,但并没有给出两者的换算关系。
因此,本研究在开发3 m直尺下最大间隙指标和国际平整度指数IRI计算程序的基础上,以实测的37条跑道和37条滑行道的纵断面高程为不平整激励输入,分别计算两个指标之间的相关性,并定量分析不同分段统计间隔对相关性的影响。分析这两个指标的敏感波长,揭示两者相关性强弱的内因。
1 国际平整度指数
设定一个标准1/4车模型以80 km/h的稳定速度行驶在路面上,以单位距离内的车辆动态反应悬挂系的累积竖向位移量作为国际平整度指数IRI,故IRI反映的是一段距离的平整度平均状况,对于给定的断面高程也可经过力学模型计算后得到。
1.1 1/4车模型
标准的1/4车模型如图1中所示。非簧载质量代表了车辆减震器下部的底盘构件,簧载质量代表了减震器上部的构件。Ms为簧载质量;Mu为非簧载质量;Ks为车身悬架刚度系数;Cs为车身悬架阻尼系数;Ku为轮胎刚度系数;q为不平整激励;Zs为簧上质量Ms的绝对位移;Zu为非簧上质量Mu的绝对位移。
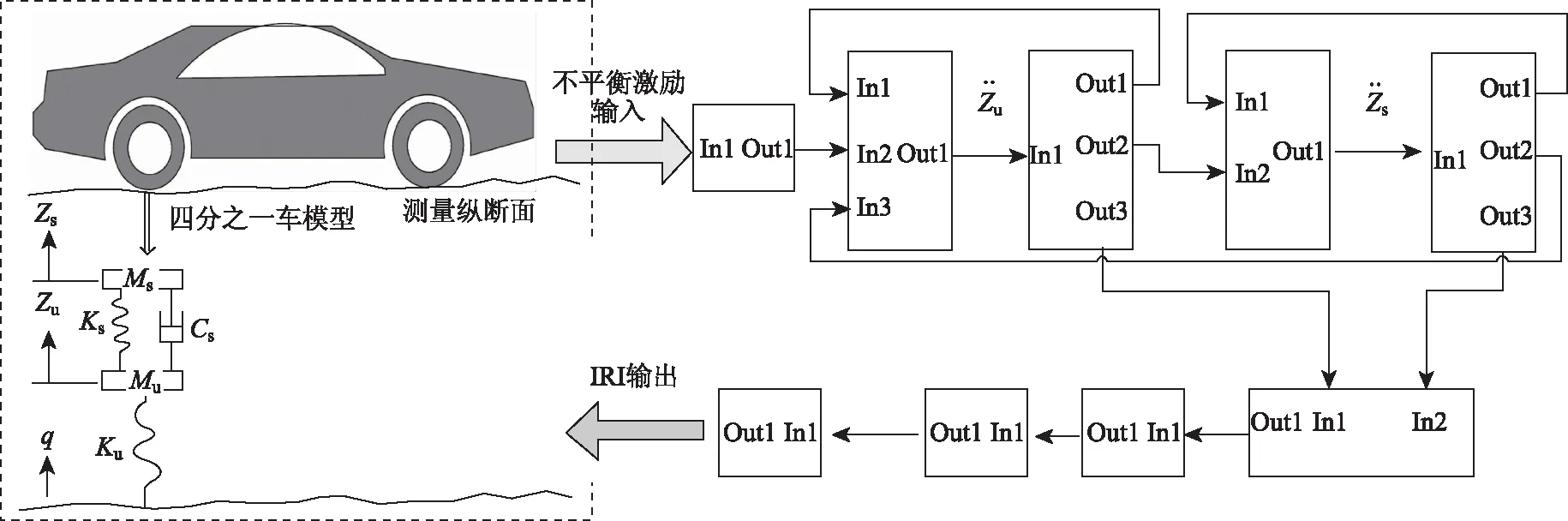
图1 1/4车模型及Simulink求解Fig.1 Quarter car model and Simulink solution
在不平整激励作用下,根据牛顿第二定律,非簧载质量和簧载质量的振动平衡方程分别如式(1)和式(2)所示:
(1)
(2)
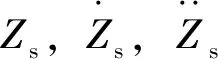
将式(1)和式(2)两边同时除以Ms,简化后的振动平衡方程如式(3)和式(4)所示:
(3)
(4)
式中,C=Cs/Ms;K=Ks/Ms;U=Mu/Ms;K′=Ku/Ms。
1.2 IRI求解
根据世界银行的定义,IRI为单位距离内簧载质量Ms和非簧载质量Mu的相对位移累计值,由式(5)计算,相应的求解流程如图1所示[6]。
(5)
式中,L为所测路段长度;v为行驶速度;t为行驶时间[2]。
2 3 m直尺下最大间隙的平均值
2.1 定义
3 m直尺下的最大间隙值是指采用一把3 m长的检测直尺,沿着纵断面放置于道面的表面,道面表面离直尺的最大高度作为3 m直尺下的最大间隙值,如图2所示。
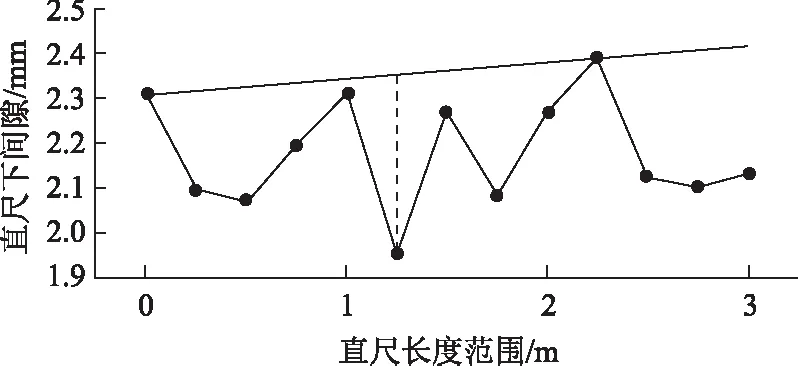
图2 3 m直尺下最大间隙值的计算Fig.2 Calculation of maximum clearance of 3 m straight edge
2.2 3 m直尺下最大间隙平均值计算流程
计算3 m直尺下最大间隙值,并根据不同统计间隔计算其平均值的流程, 如图3所示。
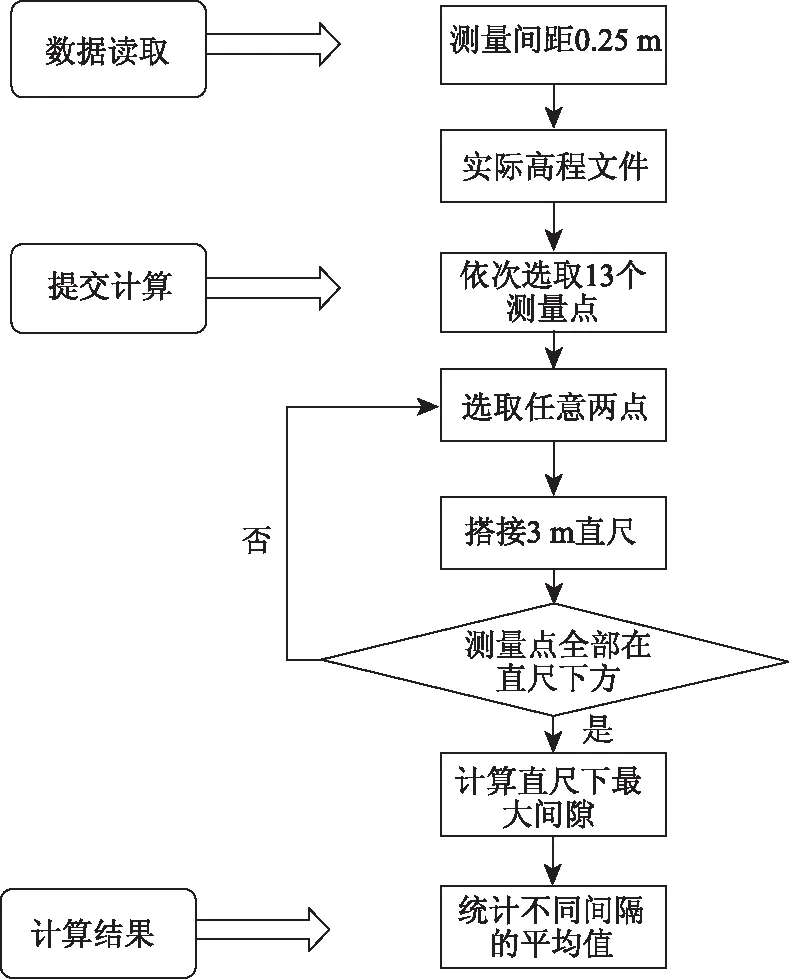
图3 3 m直尺下最大间隙平均值计算流程Fig.3 Flowchart of calculatiing average of maximum clearance of 3 m straight edge
(1)数据读取:FAA建议跑道纵断面高程数据的实测间距为0.25 m,因此该程序读取的高程数据默认为0.25 m的测量间距。
(2)提交计算:先找到搭接在13个测量点上方的3 m直尺位置,再计算3 m直尺下最大间隙值。
(3)计算结果:计算结果得到每个测量点的3 m 直尺下最大间隙值,并根据需要,可以统计不同间隔的平均值。
3 指标的相关性
3.1 试验设计3.1.1 实测纵断面高程数据
美国联邦航空总局(FAA)、波音公司和空客公司曾实测了世界范围内37条跑道和37条滑行道的纵断面高程数据[15-16]。通过车载传感器测得信号(某跑道数据如图4所示),然后积分计算得到道面的断面高程,并通过高通滤波消除传感器的漂移误差。值得说明的是,图4采用的车载式激光平整度仪所测量的是跑道短距离内的相对高程,不能反映长距离范围内的高程变化和飞机颠簸效应,但是对计算IRI值和3 m直尺下最大间隙并无影响。因此,本研究分别将世界范围内实测的37条跑道和37条滑行道经过去噪和过滤后的数据作为输入,分析在不同分段统计间隔下IRI指标的平均值和3 m直尺下最大间隙的平均值的相关性,结果具有一定的可靠性和代表性。
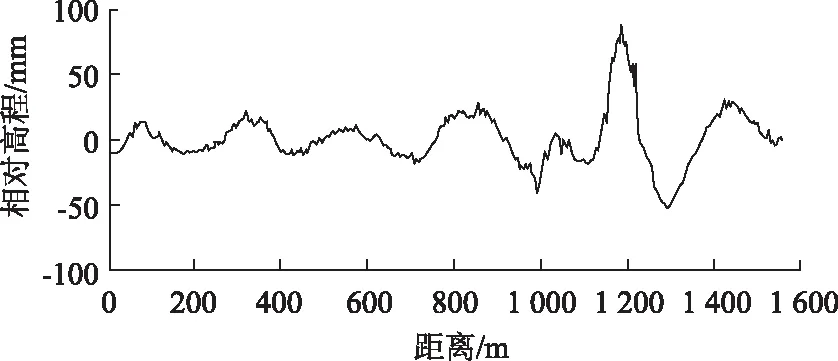
图4 某跑道的纵断面实测高程Fig.4 Measured longitudinal profile elevation of a runway
3.1.2相关性分析
相关性分析又称线性相关性分析,用来衡量两个变量之间是否存在线性关系,进而判断存在线性关系的两个变量之间的相关程度的强弱。相关系数r的计算公式如式(6)所示,相关程度判断标准如表1所示。
(6)
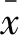

表1 相关程度判断标准Tab.1 Criterion for correlation degree judgment
实际的平整度采用3 m直尺检测是单个板多方向的检测,但由于本研究基于的是跑道纵断面不平整数据,2.2节的程序计算的是纵向的直尺最大间隙,因此利用式(6)得到的相关性是针对跑道纵向不平整的。
3.2 结果分析3.2.1 机场跑道
(1)线性关系
以20 m作为指标统计的分段间隔,IRI值与3 m直尺下最大间隙的平均值对应关系如图5所示。37条跑道共统计2 909个样本点,所有样本点的分布呈线性趋势,且随着3 m直尺下最大间隙的平均值的增大,IRI值也增大。对所有的点进行线性相关性分析,发现两者的相关系数r高达0.95,属于高度正线性相关。结果表明,IRI值与3 m直尺下最大间隙两者之间具有很强的线性关系,IRI值为3 m直尺下最大间隙的平均值的0.86倍,两者可互换。
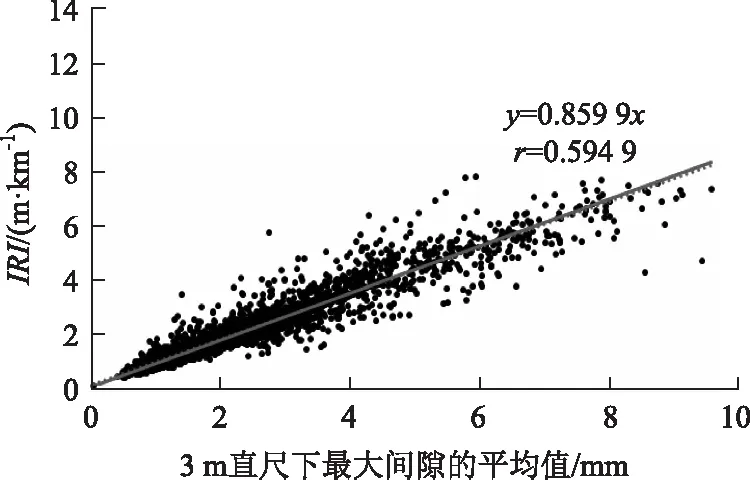
图5 IRI与3 m直尺下最大间隙平均值的相关性Fig.5 Correlation between IRI and average of maximum clearance of 3 m straight edge
(2)不同分段间隔
对于跑道而言,不同分段间隔统计对两个指标的相关系数r的影响如图6所示。可见,对于10~100 m的分段间隔,r分布在0.94~0.97之间,都属于高度线性相关。随着分段间隔的增加,r呈现逐渐增大的趋势,统计各相关系数的平均值、方差和变异系数如表2所示,相关系数的平均值为0.96,变异系数仅为0.01,这表明分段间隔对相关系数的影响不大。因此,在跑道的平整度检测时,无论对于多大的分段间隔,IRI值为3 m直尺下最大间隙的平均值的0.86倍线性关系仍然适用。
图6 相关系数随分段间隔的变化趋势Fig.6 Trend of correlation coefficient varying with sectional interval
表2 不同分段间隔下相关系数的统计值
Tab.2 Statistics of correlation coefficient with differentsectional intervals

不同分段间隔下r的统计值指标平均值标准差变异系数跑道0.960.010.01滑行道0.970.010.01
3.2.2机场滑行道
(1)线性关系
以20 m作为指标统计的分段间隔,IRI值与3 m直尺下最大间隙的平均值对应关系如图8所示。
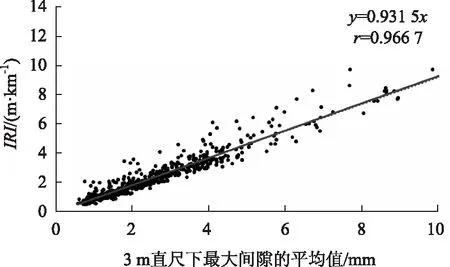
图8 IRI值与3 m直尺下最大间隙的平均值相关性Fig.8 Correlation between IRI and average of maximum clearance of 3 m straight edge
可见,37条滑行道592个样本点的分布也呈线性趋势,且随着3 m直尺下最大间隙的平均值的增大,IRI值也增大。对所有的点进行线性相关性分析,发现两者的r高达0.97,也属于高度正线性相关。结果表明,IRI值与3 m直尺下最大间隙两者具有很强的线性关系,IRI值为3 m直尺下最大间隙的平均值的0.93倍,两者的数值之间可相互转换。
(2)不同分段间隔
对滑行道而言,在不同分段间隔统计下,两个指标的r分布如图9所示。
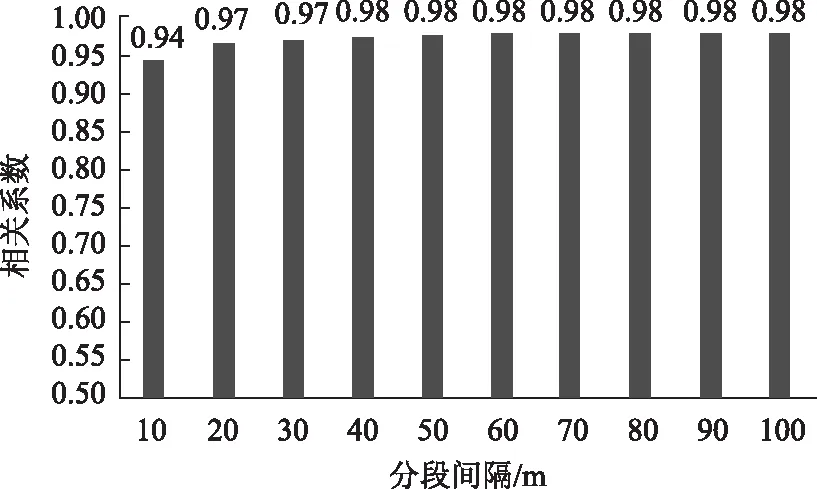
图9 相关系数随分段间隔的变化趋势Fig.9 Trend of correlation coefficient varying with sectional interval
可见,对于10~100 m的分段间隔,r分布在0.94~0.98之间,都属于高度线性相关。随着分段间隔的增加,r呈现逐渐增大的趋势,统计各相关系数的平均值、方差和变异系数如表2所示,r的平均值为0.97,变异系数仅为0.01,这表明分段间隔对相关系数的影响不大。因此,在滑行道的平整度检测时,无论分段间隔取值多大,IRI值为3 m直尺下最大间隙平均值的0.98倍线性关系仍然适用。
4 指标的敏感波长
多数学者分析了IRI指标的敏感波长,如凌建明等[6]分析了在振幅不变情况下IRI值随波长的变化特征。结果表明,IRI指标对1~5 m的短波非常敏感;在10~15 m的波段内变化相对缓和;当波长大于30 m 后,IRI接近于0。本研究采用小波分析技术分析3 m直尺最大间隙平均值的敏感波长。利用Daubechies3小波对路面不平整信号进行10层小波分解[17-18],其中的d1,d2,d3频带对应的波长分别为0.5~1 m,1~2 m,2~4 m的短波波形起伏,将三者相加即可得到波长在3 m左右的波形情况。从图10中对比直尺和小波分析的波长λ=0.5~4 m的频带可发现,直尺可以很好地反映d1+d2+d3的短波波形的起伏大小、位置,且两者的相关性极高(图11),这表明3 m直尺最大间隙指标的敏感波长范围为0.5~4 m左右。
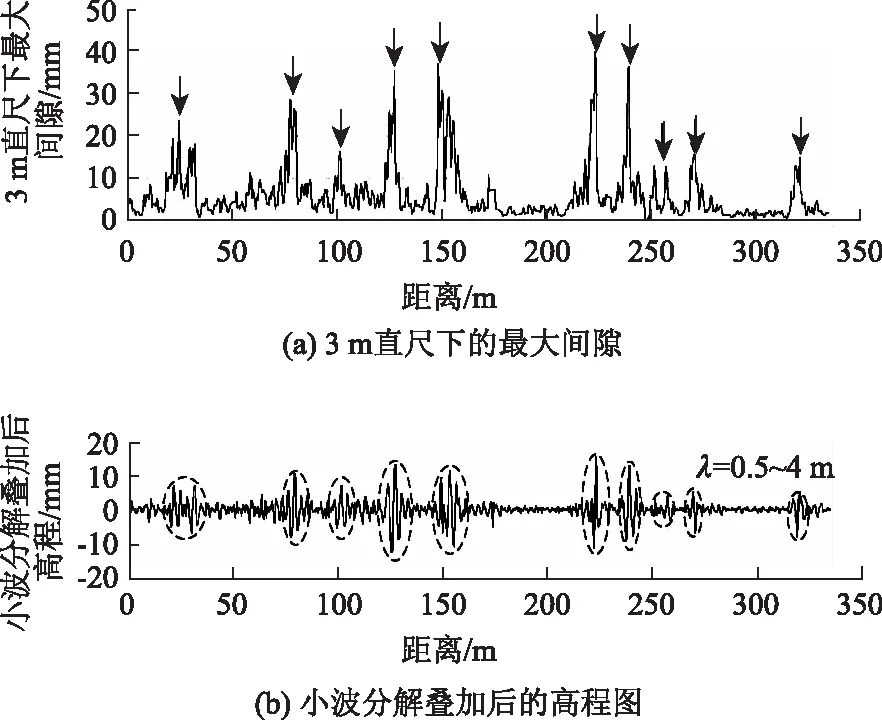
图10 3 m直尺间隙值与小波波形对比Fig.10 Comparision of clearance of 3 m straight edge and wavelet waveform
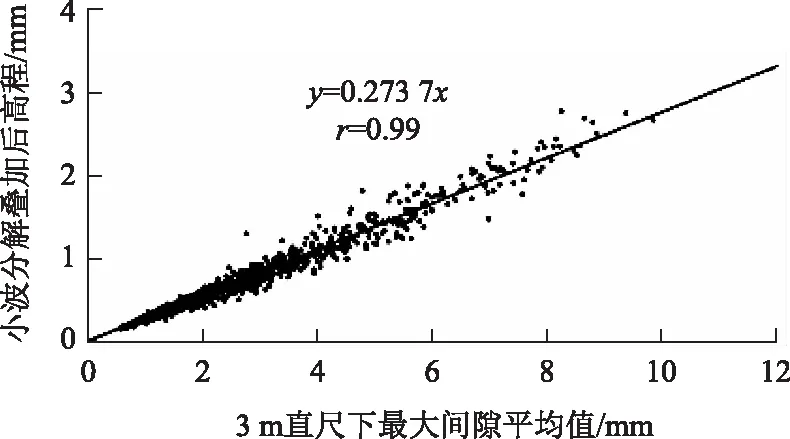
图11 3 m直尺间隙值与小波波形相关性Fig.11 Correlation between clearance of 3 m straight edge and wavelet waveform
由上述分析可知,两个指标都对道面上的0~5 m 左右的短波敏感,敏感波长相似使得无论是在机场跑道还是滑行道,IRI和3 m直尺下最大间隙的平均值之间都呈现高度线性相关。
本研究结论中,对于跑道和滑行道,IRI分别为3 m直尺下最大间隙平均值的0.86倍和0.93倍;文献[12-13]得到的公路路面的平整度标准差为IRI值的0.60倍左右;文献[11]根据实测的290段公路路面平整度数据,得到平整度标准差为IRI值的0.70倍左右。显然,机场道面和公路路面所对应的两者之间的相关关系不一样。这是因为机场道面修筑的年限、环境、地基类型、结构形式、作用荷载、维修频率等与公路路面差异较大,这将导致这两类铺面的平整度恶化方向和幅度都不一样。换言之,机场道面和公路路面的不平整起伏中各种频谱组成都不一样,一般的趋势是机场道面的长波成分较多、公路路面的短波成分较多,不同波长的敏感性不一样导致IRI和3 m直尺之间的相关性存在差异。
5 结论
(1)建立了国际平整度指数IRI的Simulink快速求解流程,开发了3 m直尺下最大间隙平均值计算方法,提出了两个指标之间相关性研究的方法。
(2)无论是在跑道还是滑行道,两个指标之间的相关系数r都大于0.95,属于高度线性相关,且分段间隔的取值对相关程度基本无影响。
(3)对于跑道和滑行道,IRI分别为3 m直尺下最大间隙平均值的0.86倍和0.93倍。两者的线性关系可提供延续机场道面历史资料信息的一种有效途径,为机场道面的性能预测提供更多的基础样本。
(4)3 m直尺下最大间隙平均值的敏感波长为0.5~4 m的短波,与IRI的敏感波长1~5 m短波非常接近,揭示了两个指标之间相关性强的内在原因。
——以上海浦东国际机场为例

